Informatik an der Fernuni

Update: Index-Fehler zu \(I_1\) (Danke, Martin!)

Update: auch hier habe mich mich noch strikter an die Lernziele gehalten. Zusätzlich dazu wurden noch ein paar Beispiele zu entscheidbaren und semi-entscheidbaren Funktionen eingepflegt um das Verständnis zu erleichtern, was mir hoffentlich gelungen ist 😉

Update 2: ich merke gerade, dass die Einträge zu lang sind. Selbst die Ladezeiten vom Chrome sind bei den Mathe-Symbolen für 10 Seiten exorbitant hoch. Ich habe daher beschlossen die Beiträge daher zu trennen.

Es gibt insg. drei vier Beiträge zur KE6.

• TIA: Rekursive und rekursiv-aufzählbare Mengen (Lernziele KE6, 1/4)
• TIA: Bild- und Projektionssatz (Lernziele KE6 2/4)
• TIA: Halte- Äquivalenz- und Korrektheitsproblem, Reduzierbarkeit, Satz von Rice (Lernziele KE6, 3/4)
• TIA: Gödel’scher Unvollständigkeitssatz (Lernziele KE6, 4/4)

Da die Lernziele im Skript etwas verstreut sind, kann es sein, dass ich etwas springen muss und nicht alles der Reihe nach abhake. Lasst euch davon nicht verwirren.

Dieser Eintrag befasst sich mit rekursiven und rekursiv-aufzählbaren Mengen und ihren Eigenschaften. Wir hatten bereits in den anderen Beiträgen viel mit Mengen zu tun. Ich werde die Erklärungen hier einfach Copy&Pasten, falls sie passen.

Lernziel 1 und 3

Definition rekursiver und rekursiv aufzählbarer Mengen von Zahlen und Wörtern

Zunächst einmal hilft es sich wie Bart bei den Simpsons 100x „Rekursiv = entscheidbar. Rekursiv aufzählbar = Semi entscheidbar“ wahlweise in das Parkett zu kratzen, die Wand zu tapezieren oder sich auf die Stirn tätowieren zu lassen. Nachdem das erledigt ist, wiederholt man das Gleiche dann noch mit der Definition (welche ich aus diesem Beitrag zur Entscheidbarkeit einfach Copy&Paste):

Eine Menge \( T \subseteq M\) ist entscheidbar/rekursiv wenn die charakteristische Funktion \(\chi_T: M \rightarrow \{0,1\}\) definiert durch

\(\chi_T(t)=\begin{cases} 1, & \mbox{ falls } t \in T \\ 0, & \mbox{ sonst}\end{cases}\)

berechenbar ist (Achtung: sie muss berechenbar sein und nicht einfach nur existieren!).

Achtung: die charakteristische Funktion existiert immer und ist im Falle der Entscheidbarkeit auch immer total!

Dann nochmal für r.a.:

Eine Menge \(T\) ist semi-entscheidbar/rekursiv aufzählbar wenn die partielle charakteristische Funktion \(\chi^{‚}_T: M \rightarrow \{1\}\) definiert durch

\(\chi^{‚}_T(t)=\begin{cases} 1, & \mbox{ falls } t \in T \\ \perp, & \mbox{ sonst}\end{cases}\)

berechenbar ist.

Achtung: hier existiert die charakteristische Funktion ebenfalls, sie ist aber nicht mehr total!

Manchmal sagt man auch, dass die „halbe“ charakteristische Funktion berechenbar ist. Oder wie im Skript ausgedrückt:

Eine Menge \(T\subseteq\mathbb{N}^k\) ist semi-entscheidbar/rekursiv aufzählbar wenn es eine partielle berechenbare Funktion \(f:\subseteq\mathbb{N}^k\rightarrow\mathbb{N}\) gibt mit \(T=Def(f)\).

Während sich die Definition für r.a. Mengen über die charakteristische Funktion noch erschließen mag, ist es bei dieser hier ein bisschen abstrakter.

Denkt euch eine Menge \(T\), wo Ihr nur entscheiden könnt ob ein Element zu dieser Menge gehört, aber nicht ob es nicht dazu gehört (sie ist also offensichtlich nur semi-entscheidbar). Und nun lasst Ihr die charakteristische Funktion \(f\) aus der 2. Definition auf jedem Element \(x\) dieser Menge \(A\) laufen.

Gehört das Element \(x\) zu dieser Menge \(T\), so ist die Ausgabe der Funktion \(f(x)=1\). Und das für jedes \(x\in{A}\), dass zur Menge \(T\) gehört. Gehört es nicht zur Menge \(T\), so rechnet die Funktion unendlich lange weiter. Damit sind alle positiv entschiedenen Elemente \(x\in A\) in der Menge \(T\) und ganz \(T\) damit der Definitionsbereich der Funktion \(f\), eben \(T=Def(f)\).

Wenn wir also entscheiden können ob ein Element in einer Menge ist oder nicht, ist die Menge rekursiv (z.B. bei der Entscheidung auf Primzahlen). Können wir nur positive (oder nur negative, aber nie beides) Entscheidungen treffen ob sich das Element in der Menge befindet (z.B. bei dem Halteproblem), dann ist die Menge nur rekursiv aufzählbar. Nicht vergessen: eine rekursive Menge ist auch rekursiv aufzählbar, aber eine rekursiv aufzählbare Menge nicht zwingend rekursiv.

Später kommen wir noch zu ein paar Beispielen für diese Mengen.

Eine weitere, wichtige Eigenschaft für rekursive Funktionen ist die folgende:

Eine unendliche Menge \(A\subseteq\mathbb{N}\) ist rekursiv, gwd. es eine wachsende, totale Funktion \(f\) gibt mit \(A = Bild(f)\). Wachsend bedeutet: \(f(n) < f(n+1)\)

Höre ich euch die Augenbrauen zusammenziehen? Müsst Ihr nicht. Es ist nicht schwer: was eine wachsende Funktion ist, wisst Ihr sicherlich: es ist eine Funktion, dessen Funktionswert bei der Eingabe vom Parameter \(n\) stets kleiner ist als bei der Eingabe von \(n+1\).

Beispiel: \(f(n)=n^2\)

Stellen wir für \(1\leq{n}\leq{5}\) mal die Funktionswerte zusammen:

\(f(1)=1,f(2)=4,f,(3)=9,f(4)=16,f(5)=25\)

Kein Funktionswert von \(f(n+1)\) ist kleiner als \(f(n)\). Damit ist sie wachsend.

Schaffen wir es also so eine Funktion \(f\) anzugeben, wo die Ausgabe (sog. Bildmenge) von \(f\) unsere komplette Menge \(A\) ist, so ist die Menge \(A\) entscheidbar/rekursiv.

Exkurs Nr. 2: weiterhin sind alle endlichen Mengen rekursiv/entscheidbar. Warum? Nehmen wir einfach eine beliebige, endliche Menge \(A\subseteq\mathbb{N}\). Egal welche Eigenschaften wir dieser Menge zuordnen, so können wir (theoretisch) einfach eine riesige charakteristische Funktion angeben, die für jedes Element entscheidet ob es zu \(A\) gehört oder nicht. Denn die Menge ist endlich.

Nun solltet Ihr einen kleinen Eindruck davon bekommen haben was entscheidbar/rekursiv und was semi-entscheidbar/rekursiv-aufzählbar ist.

Exkurs Nr. 3: Zusammenhang zu Wörtern

Der Zusammenhang zwischen Zahlen und Wörtern sollte nach der Standardnummerierung \(\sigma\) der Wörter über \(\Sigma^*\) sollte euch bereits klar sein. Denn alles, was wir über Mengen auf \(\mathbb{N}^k\) oder \(\mathbb{N}\) aufzählen, gilt selbstverständlich auch für Mengen über einem Alphabet \(\Sigma^{*}\).

Mittels Standardnummerierung können wir Worte aus einem Alphabet \(\Sigma\) nummerieren und umgekehrt. Das haben wir im Beitrag über \(\nu_\Sigma\) bereits erfolgreich getan.

Ebenfalls konnten wir Bandprogramme \(BP\) erfolgreich mit \(\nu_P\) nummerieren und entscheiden ob ein Wort über dem „Programmiersprachenalphabet“ \(\Omega^{*}\) ein Bandprogramm ist oder nicht. Damit ist die Menge der Bandprogramme \(BP\), der PASCAL-Programme und die Menge der \(WHILE\)-Programme entscheidbar/rekursiv.

 

Antwort zum Lernziel: eine Menge ist rekursiv/entscheidbar wenn ihre (volle) charakteristische Funktion berechenbar ist. Für eine nur semi-entscheidbare/rekursiv-aufzählbare Menge muss nur die „halbe“ charakteristische Funktion berechenbar sein.

Im ersten Fall können wir damit die vollständige Menge \(A\) entscheiden, d.h. ob ein Element zu dieser gehört oder nicht (formal ausgedrückt: \(x\in{A}\) und \(x\notin{A}\)). Im letzten Fall können wir nur positiv oder negativ entscheiden, aber nie beides gleichzeitig (formal ausgedrückt: \(x\in{A}\) oder \(x\notin{A}\), aber nicht beides gleichzeitig).

Eine Art Ausnahme bildet das Komplement einer semi-entscheidbaren Menge: können wir dieses ebenfalls semi-entscheiden, so ist die komplette Menge entscheidbar. Denn damit haben wir im Endeffekt die positive und negative Antwort, d.h. die „volle“ charakteristische Funktion berechnet.

Lernziel 4

Abschlusseigenschaften rekursiver und rekursiv aufzählbarer Mengen

Im Skript werden die folgenden, abschließenden Eigenschaften von rekursiven/entscheidbaren Mengen genannt:

1. \(A_1, A_2 \subseteq \mathbb{N}^k\) rekursiv. Damit ist auch \(\mathbb{N}^k\setminus A_1, A_1 \cup A_2\) und \(A_1 \cap A_2\) rekursiv.

2. Sei \(A \subseteq \mathbb{N}\) rekursiv, sei \(f \in R^{(1)}\). Dann ist \(f^{-1}[A]\) rekursiv.

3. Sei \(A \subseteq \mathbb{N}^k\), dann gilt: \(A\) rekursiv \(\Longleftrightarrow \pi^{(k)}[A]\) rekursiv.

Die 1. Eigenschaft ist soweit deutlich: \(A_1\) und \(A_2\) sind Teilmengen aus \(\mathbb{N}^k\) mit eben der Stelligkeit \(k\). Restmenge, Vereinigungsmenge und Schnittmenge sind damit auch rekursiv.

Eigenschaft Nr. 2 ist etwas aufwändiger wenn Ihr mit der Schreibweise nicht vertraut seid und (wie ich) Abschnitt 1.3 überlesen habt. Daher hier zur Auffrischung nochmal. Einer Korrespondenz wird eine Funktion \(f\) zugeordnet, die Mengen transformiert. Die Umkehrfunktion davon \(f^{-1}[A]\). Wenn die Menge \(A\) nun rekursiv ist und es eine totale Funktion \(f\) gibt, so ist auch die Umkehrfunktion rekursiv.

Durch die Cantorfunktion aus Eigenschaft Nr. 3 können wir uns bei unseren Untersuchungen auf die rekursiven Teilmengen von \(\mathbb{N}\) beschränken. Wir erinnern uns: wie können mit dieser Funktion \(\pi\) beliebige \(k\)-stellige Tupel auf eine natürliche Zahl aus \(\mathbb{N}\) abbilden. Wer sich nicht dran erinnert, sollte sich nochmal den Beitrag zu Gemüte führen.

Wir haben damit sichergestellt, dass Operatoren die rekursiven Mengen auch wieder in rekursive Mengen transformieren.

Anschließend folgen die Abschlusseigenschaften der rekursiv aufzählbaren/semi-entscheidbaren (r.a.) Mengen:

1. \(A_1, A_2 \subseteq \mathbb{N}^k\) r.a. Damit ist auch \(A_1\cup A_2\) und \(A_1 \cap A_2\) r.a.

2. Sei \(A \subseteq \mathbb{N}\) r.a., sei \(f \in P^{(k)}\). Dann ist \(f^{-1}[A]\) r.a.

3. Sei \(A \subseteq \mathbb{N}^k\), dann gilt: \(A\) r.a. \(\Longleftrightarrow \pi^{(k)}[A]\) r.a.

Die Erläuterung erfolgt analog zu rekursiven Mengen. Bitte aber beachten, dass wir nun auf den partiellen, mehrstelligen, berechenbaren Funktionen \(P^{(k)}\) arbeiten und nicht mehr auf den totalen \(R^{k}\).

Zusammenfassend zitiere ich aus der Wikipedia für die rekursiven/entscheidbaren und rekursiv-aufzählbare/semi-entscheidbare Mengen:

• Jede entscheidbare Menge ist rekursiv aufzählbar, aber es gibt rekursiv aufzählbare Mengen, die nicht entscheidbar sind.
• Eine Menge ist genau dann entscheidbar, wenn sie und ihr Komplement rekursiv aufzählbar sind.
• Jede endliche Menge ist rekursiv aufzählbar.
• Jede rekursiv aufzählbare Menge ist abzählbar, aber nicht alle abzählbaren Mengen sind rekursiv aufzählbar.
• Jede unendliche rekursiv aufzählbare Menge besitzt Teilmengen, die nicht rekursiv aufzählbar sind.
• Der Schnitt von endlich vielen rekursiv aufzählbaren Mengen ist rekursiv aufzählbar; die Vereinigung einer rekursiv aufzählbaren Menge von rekursiv aufzählbaren Mengen ist rekursiv aufzählbar. Es gibt rekursiv aufzählbaren Mengen, deren Komplement nicht rekursiv aufzählbar ist.

Antwort zum Lernziel: die entscheidbaren Mengen sind abgeschlossen bzgl. Komplement, Schnitt und Vereinigung. Die semi-entscheidbaren mengen jedoch nur bzgl. Schnitt und Vereinigung, das Komplement ist nicht semi-entscheidbar (wäre es das, so wäre die Menge vollständig entscheidbar. Siehe vorheriges Lernziel).

Lernziel 2a

Nachweis der Rekursivität/Entscheidbarkeit von Mengen

Was tun wir um die Rekursivität von Mengen zu beweisen? Wir geben ein Flussdiagramm einer verallgemeinerten Registermaschine an, welches die charakteristische Funktion für die zu untersuchende Menge berechnet. Wir entscheiden nun wirklich ob ein Element in der rekursiven Menge ist oder nicht. Dazu verwenden wir alle bereits als berechenbar bewiesenen Funktionen. Mehr nicht.

Hilfreich ist hierfür die Auflistung der berechenbaren Funktionen aus Satz 3.2.5:

• Nullfunktion
• Nachfolger- und Vorgängerfunktion
• Projektion
• konstante Funktion
• Summe
• arithmetische Differenz
• Produkt
• Quotient und Rest
• Exponentation
• Wurzel
• max/min
• Primzahltest und \(x\)-te Primzahl

Könnt ihr alle für euer Flussdiagramm benutzen 😉

Beispiel? Sicher: \(T=\{x\in\mathbb{N}\mid x\text{ ist Primzahl}\}\)

Die dazu notwendige, charakteristische Funktion ist:

\(\chi_T(x)=\begin{cases} 1, & \mbox{ falls } x\text{ Primzahl} \\ 0, & \mbox{ sonst}\end{cases}\)

Test auf Primzahl: Für alle \(y\) mit \(1<y<x\) wird getestet ob es bei der Division von \(x\) durch \(y\) einen Rest gibt. Gibt es bei einem \(y\) keinen Rest, so ist es keine Primzahl (dann ist \(y\) nämlich ein legitimer Teiler von \(x\)).

Damit können wir für jedes \(x\in\mathbb{N}\) entscheiden ob es eine Primzahl ist oder nicht. Das Flussdiagramm für den Test dürft Ihr selbst angeben 😉

Ein weiteres Beispiel wäre z.B. der Test auf die Goldbach-Eigenschaft einer Zahl.

Antwort zum Lernziel: um zu zeigen, dass eine Menge entscheidbar/rekursiv ist, muss die (volle) charakteristische Funktion berechenbar sein.

Dazu gibt man das Flussdiagramm einer verallgemeinerten Maschine (wenn man streng ist, muss man für jeden verallgemeinerten Test seine Berechenbarkeit ebenfalls nachweisen und letztendlich seine Maschine auf die drei Grundoperationen Addition/Subtraktion von \(1\) und Test auf \(0\) zurückführen) an, die diese berechnet und in jedem Fall mit einem Ergebnis hält.

Lernziel 2b

Nachweis der rekursiven Aufzählbarkeit/Semi-entscheidbarkeit von Mengen

Auch hier ist es nicht allzu schwierig. Jede rekursiv aufzählbare (semi entscheidbare) Menge ist auch gleichzeitig aufzählbar und jede aufzählbare Menge ist auch rekursiv aufzählbar (semi entscheidbar). Daher müssen wir es nur schaffen, die Elemente der Menge irgendwie  aufzuzählen. Man macht sich leicht klar, dass der Definitionsbereich und Wertebereich von berechenbaren Funktionen rekursiv aufzählbar ist.

Aber was ist mit \(n\)-Tupeln? Die sind dank Cantor’schen Tupelfunktion auf ein Element reduzierbar, d.h. wir können \(n\)-Tupel auf einelementige Mengen reduzieren und unseren Schabernack mit ihnen treiben.

Wird also gefragt, ob eine Menge rekursiv aufzählbar ist, so geben wir einfach eine charakteristische Funktion an, die die Eigenschaft der Menge nur positiv (oder nur negativ) beantwortet. Für die gegensätzliche Antwort muss unsere charakteristische Funktion (im Gegensatz zur vollen charakteristischen Funktion für entscheidbare Mengen) nicht halten, Hauptsache sie sagt uns zuverlässig eine der beiden Antworten. Ein gutes Beispiel ist das Post’sche Korrespondenzproblem.

Beispiel: Post’sches Korrespondenzproblem

Das Post’sche Korrespondenzproblem beschreibt das Problem bei Wortpaaren \((x_1,y_1),…,(x_n,y_n)\) eine Folge \(i_1,…,i_k\) mit der Eigenschaft: \(x_{i_1}x_{i_2}…x_{i_k} = y_{i_1}y_{i_2}…y_{i_k}\) zu finden. Ist natürlich wieder etwas abstrakt, aber probieren wir das mal an einem Beispielproblem:

Beispielproblem \(P=((01,1),(0,000),(01000,01))\)

\(P\) nennt man Problemfall oder Instanz.

Fragestellung: gibt es eine Lösung (d.h. eine Folge von Indices) \(I\) zum Problemfall \(P\)? Wenn ja, ist die Folge eine Lösung von \(P\).

Wir müssen hier also eine Kombination von zwei Wortkombinationen \(\omega_1 = \omega_2\) finden und die folgenden Regeln einhalten:

• \(\omega_1\) darf nur aus den 1. Elementen der 3 Wortpaare bestehen: \(01,0\) und \(01000\).
• Das Wort \(\omega_2\) darf nur aus den 2. Elementen der 3 Wortpaare bestehen: \(1,000\) und \(01\).
• Die Wortkombinationen \(\omega_1\) und \(\omega_2\) dürfen beliebig lang sein.

Was Indices sind, ist euch klar? Nein, keine Sorge. Kommt gleich. Es liegt also an unserer Kombinationsgabe eine passende Index-Kombination zu finden, so dass am Ende gilt: \(\omega_1=\omega_2\).

Eine mögliche Lösung wäre \(\omega_1 = 01000\mid{0}\mid{0}\mid{01}\) und \(\omega_2=01\mid{000}\mid{000}\mid{1}\). (die \(\mid\) sind nur optische Trennzeichen damit Ihr die Elemente identifizieren könnt aus denen die Worte bestehen).

Die zugehörigen Indices wären: \(I_1=(3,2,2,1)\). Damit ist \(I_1\) eine Lösung für \(P\) und \(P\) damit gelöst.

Die Indices sind nichts weiter als die Nummer des Tupels, dass zur Bildung herangezogen wird. Da wir für das erste Wort \(\omega_1\) nur die ersten und für das zweite Wort \(\omega_2\) nur die zweiten Elemente aus den Tupeln benutzen dürfen, reicht uns als Angabe einfach nur die Nummer des Tupels.

Würden wir z.B. die folgende Lösung austesten wollen: \(I_2=(2,3,1,1)\), so wären die Worte \(\omega_1\) und \(\omega_2\):

\(\omega_1=0\mid{01000}\mid{01}\mid{01}\) und

\(\omega_2=000\mid{01}\mid{1}\mid{1}\)

Da \(\omega_1\neq\omega_2\), ist die mögliche Lösung \(I_2\) falsch und \(P\) noch nicht gelöst. Aber was nicht ist, kann ja noch werden!

Um zu zeigen, dass die Menge dieser Worttupel rekursiv aufzählbar/semi entscheidbar ist brauchen wir nur zu zeigen, dass die Menge der Definitionsbereich einer partiellen Funktion ist und die dazugehörige Maschine anzugeben, welche die charakteristische Funktion für diese Menge berechnet und in jedem Fall mit einer \(1\) terminiert wenn das Element in der Menge ist oder nicht terminiert, wenn es das nicht ist.

Die charakteristische Funktion für dieses Problem wäre:

\(\chi^{‚}_P(I)=\begin{cases} 1, & \mbox{ falls }\omega_1=\omega_2 \\ \perp, & \mbox{ sonst}\end{cases}\)

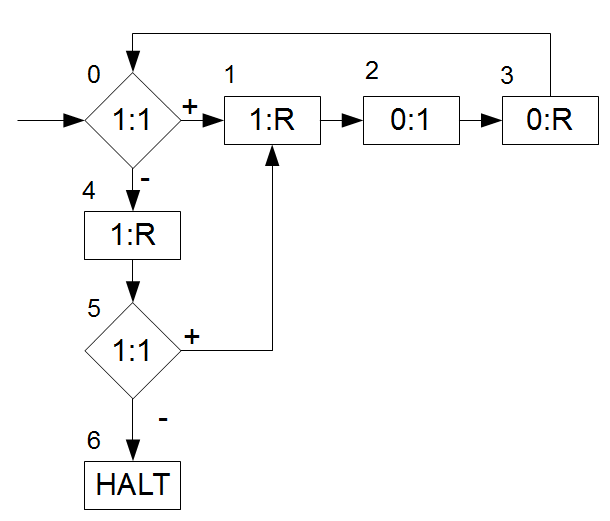
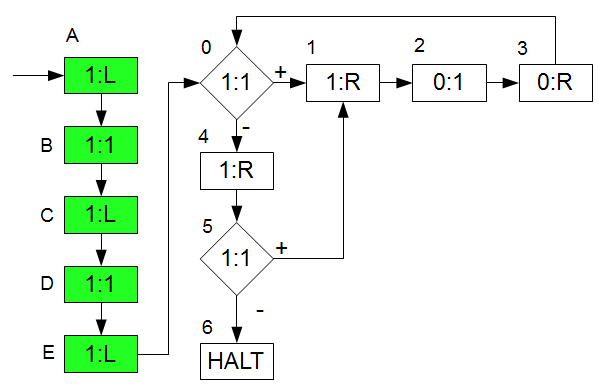
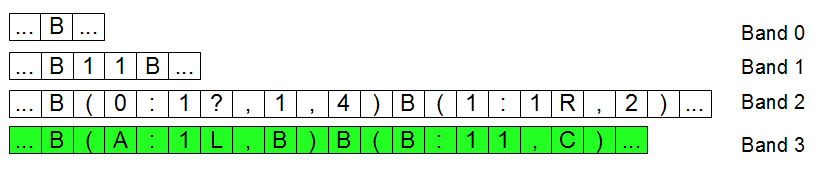
Das Flussdiagramm beschreibe ich hier ebenfalls am besten in Pseudocode:

1. Setze \(n=1\)
2. Fange mit einer Indexfolge \(I\) der Länge \(n\) an
3. Erstelle durch den Index \(I\) die Worte \(\omega_1\) und \(\omega_2\) mit Länge \(n\)
4. Prüfe ob \(\omega_1=\omega_2\).

   Wenn ja, so ist eine Lösung für \(P\) gefunden: HALT!

   Wenn nein, setze \(n=n+1\) und gehe zu Punkt 2.

Wie man am Pseudocode gut erkennen kann, kann man zu einer gegebenen Probleminstanz \(P\) eine Lösung durch systematisches ausprobieren finden.

Es ist damit sichergestellt, dass wir so tatsächlich eine korrekte Lösung finden wenn es eine gibt. Und wenn nicht? Da die Länge der Indexfolge unendlich ist und unsere Worte somit unendlich lang werden, kann es sein, dass wir niemals anhalten. Im ungünstigsten Fall läuft unser Programm für eine Kombination also ewig.

So können wir nur schlussfolgern ob eine konkrete Belegung von \(I\) eine Lösung darstellt oder nicht. Aber wir werden nie wissen ob \(P\) nicht doch vielleicht eine Lösung hat.

Kleiner Exkurs: Tatsächlich können wir das Problem für eine kleine Anzahl an Paaren wirklich entscheiden (für ein oder zwei Paare ist das Problem nach Ehrenfeucht und Rozenberg (1981) entscheidbar)! Für die Anzahl zwischen zwei und drei Paaren ist es noch nicht ganz geklärt, während die Anzahl von sieben paaren bereits ausreicht um von Unentscheidbarkeit zu sprechen (Matiyasevich, 1996).

Noch ein Exkurs: Eine weitere Möglichkeit zu zeigen, dass das Post’sche Korrespondenzproblem nicht entscheidbar ist die Reduktion einer nicht entscheidbaren Menge auf dieses. Aber zum Thema Reduktion kommen wir noch in Teil B der theoretischen Informatik.

Antwort zum Lernziel: Um zu zeigen, dass eine Menge semi-entscheidbar/rekursiv-aufzählbar ist, muss die „halbe“ charakteristische Funktion berechenbar sein. Wir müssen also mit Gewissheit sagen können, ob ein Element zur Menge gehört. Das Gegenteil ist uns hier aber vergönnt und wir nehmen es in Kauf, dass unsere Testmaschine für eine Eingabe im ungünstigsten Fall ewig rechnet.

Dazu gibt muss man ebenfalls man das Flussdiagramm einer verallgemeinerten Maschine angeben, aus der ersichtlich ist, dass sie eine Eingabe in jedem Fall positiv bewertet wenn es denn eine Lösung zum gestellten Problem ist und so lange weiterrechnet bis eine Lösung gefunden ist. Im schlimmsten Fall eben ewig.

Lernziel 6

Erläuterung des Zusammenhangs zwischen rekursiven und rekursiv-aufzählbaren Mengen

Eine spannende, aber offensichtliche Beziehung zwischen entscheidbaren und semi-entscheidbaren Mengen ist: eine Menge ist entscheidbar wenn die Menge selbst und ihr Komplement semi-entscheidbar sind. Formal ausgedrückt:

Eine Menge \(A \subseteq \mathbb{N}^k\) ist rekursiv, gdw. \(A\) und \(\mathbb{N}^k\setminus A\) r.a. sind.

Nehmen wir also an, wir haben eine semi-entscheidbare Menge \(A\subseteq\mathbb{N}\). Wie wir wissen, ist sie semi-entscheidbar, d.h. wir können entscheiden ob ein Element zu dieser Menge gehört. Aber nicht das Gegenteil.

Und was wäre dann die Menge \(\mathbb{N}\setminus{A}\)? In dieser Menge wären genau die Elemente, die zwar aus \(\mathbb{N}\) sind, sich aber nicht in \(A\) befinden.

Im Endeffekt haben wir so quasi zwei „halbe“ charakteristische Funktionen, die jeweils einen Teil entscheiden, welchen die andere charakteristische Funktion nicht entschieden hat. Beide zusammen bilden dann eine „volle“ charakteristische Funktion für \(A\).

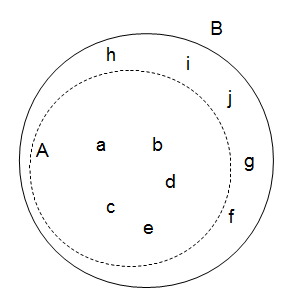
Beispiel: \(A\subseteq{B}\)

Wir können also die Menge \(A=\{a,b,c,d,e\}\) semi-entscheiden. Ob ein Element nicht in der Menge \(A\) ist hingegen nicht.

Und was wäre wenn wir das Komplement \({B\setminus{A}}\) entscheiden könnten? Also nur die Elemente \({B\setminus{A}}=\{f,g,h,i,j\}\)? Dann könnten wir für alle Elemente aus \(A\) sagen, ob sie zu Menge \(A\) gehören und für den Rest bestimmen ob sie zu \({B\setminus{A}}\) gehören. Damit würde für jedes Element eine positive und negative Entscheidung gefällt werden könne.

Und wenn das der Fall ist, ist \(A\) was? Genau! Komplett entscheidbar/rekursiv.

Die charakteristische Funktion \(cf_A\) für \(A\) wäre also:

\(\chi_A(x)=\begin{cases} 1, & \mbox{ falls } x \in A \\ 0, & \mbox{ wenn } x\in B\end{cases}\)

Fertig. Damit ist die Menge \(A\) (und natürlich auch \(B\)) rekursiv/entscheidbar.

Antwort zum Lernziel: Ist es uns möglich die Teilmenge einer anderen Menge \(A\subseteq{B}\) positiv (aber nicht negativ) zu entscheiden, so ist diese semi-entscheidbar. Können wir für den Rest, d.h. die Menge ohne die bereits positiv entschiedene Menge \(B\setminus A\) ebenfalls entscheiden, so ist die gesamte Menge \(A\) damit rekursiv/entscheidbar.

Weiter geht es mit den nächsten Lernzielen im Beitrag zum Bild- und Projektionssatz.

Bei Fehlern gilt wie immer: ASAP in die Kommentare damit.

Update: Formulierungen etwas verständlicher gemacht. Wenn euch das smn-Theorem noch nicht ganz klar, war bitte den Beitrag nochmal lesen.

Update: aus zwei macht drei. Das ist nun hoffentlich der letzte Teil zu KE5 mit einem riesen Beispiel zum smn-Theorem.

Noch einmal die Wiederholung der zwei Anforderungen an vernünftige Programmiersprachen:

• (U) Es soll einen Computer geben, der zu jedem Programm \(P\) und jedem möglichen Eingabewert \(x\) das Resultat \(\sigma(P)(x)\) berechnet und nicht hält wenn \(\sigma(P)(x)\) nicht existiert.
• (S) Zu je zwei Programmen \(P\) und \(Q\) möchte man ein Programm für die Komposition konstruieren können, d.h. es soll eine berechenbare Funktion \(h\) geben, so dass \(\sigma(h(P,Q)=\sigma(Q) \circ\sigma(P)\).

Während wir (U) mit dem utm-Theorem gut behandeln konnten, schauen wir uns jetzt (S) an:

Lernziel 5

Erklärung und Anwendung des smn-Theorems

Kommen wir nun zum smn-Theorem, unserem Übersetzungslemma. Formal ausgedrückt:

\(f \in P^{(2)}\), dann gibt es eine total-rekursive Funktion \(r \in R^{(1)}\) mit:

\(f(i,j) = \varphi_{r(i)}(j)\) für alle \(i,j \in \mathbb{N}\).

Ehm, ja. Was macht das Ding nun?

Im wesentlichen geht es darum, dass sich berechenbare Funktionen kombinieren lassen. Durch die Hintereinanderausführung lassen sich neue Funktionen und somit auch neue Programme (und damit selbstverständlich auch neue Maschinen) mit eigenen Gödelnummern \(i\) erschaffen.

Dazu werden die Funktionen einfach hintereinander ausgeführt und die Variable \(x\) als Eingabe immer wieder von Maschine zu Maschine „mitgenommen“. Da bei diesem Vorgang, abhängig von der konkreten Belegung der Variable \(x\) eine neue Maschine erschaffen wird, gibt uns unsere Funktion \(r\) diese neue Gödelnummer preis. In dieser Maschine ist die Variable \(x\) konkret belegt und fixiert. Variable \(j\) nimmt sie jedoch ganz normal an.

Dadurch ist es möglich aus Funktionen mit mehreren Argumenten Funktionen mit nur einem Argument zu erstellen, die jedoch das selbe berechnen (Currying genannt). Wir „fixieren“ sozusagen Argumente und codieren sie in unsere neuen Maschinen ein. Am Beispiel unten wird es etwas deutlicher.

Zunächst: \(R^{(1)}\) sind die berechenbaren, totalen, einstelligen Funktionen (sie sind überall in \(\mathbb{N}\) definiert). Die Funktionen in \(P^{(1)}\) müssen nicht überall definiert sein. Im Skript ist das in menschlicher Sprache beschrieben:

„Jedes Programm der Programmiersprache \(\psi\) für Zahlenfunktionen mit berechenbarer, universeller Funktion kann mit der Funktion \(r\) in die Programmiersprache \(\varphi\) übersetzt werden“

Das trifft es eig. ganz gut. Das ist jedoch nicht direkt die Formalisierung unseres \((S)\), der Zusammenhang kommt aber gleich noch.

In der Wikipedia steht zum smn-Theorem auch noch folgender Satz (den ich leicht modifiziert habe damit er besser zu uns passt):

„Die smn – Eigenschaft besagt, dass es zu einem Code \(f_M\), der mit den Parametern \(i\) und \(x\) ausgeführt wird (bzw. ausgeführt werden kann), ein Transformationsprogramm \(r\) gibt, das aus \(f_M\), \(i\) und \(x\) ein Programm \(f_{M_i}\) berechnet, welches bei der Eingabe von \(x\) das gleiche berechnet, wie \(f_M\) bei der Eingabe von \(i\) und \(x\)„

Ja, macht Sinn. Formal ausgedrückt:

\(f_M(i,x)=r(f_M,i,x)=f_{M_i}(x)\)

(Hier sind \(i\) und \(x\) Argumente, und \(f_M\) die Gödelnummer der Ursprungsmaschine, \(f_{M_i}\) ist dann die Gödelnummer der Maschine mit dem festgesetzten \(i\)).

Auch ist es nicht das eig. smn-Theorem, welches sonst überall verwendet wird und die Stelligkeit \(m + n\) nutzt, sondern eine abgewandelte Form davon (wie vieles andere im Skript auch), damit es für den Leser nicht zu einfach wird und er Zusatzliteratur heranziehen kann. Wo kämen wir denn hin?!

Als Beweis im Skript wird folgende Idee angebracht:

Zunächst machen wir uns klar, was wir suchen. Wir brauchen eine Maschine für unsere Funktion \(r\) aus der Definition.

Wir wir oben sehen, bekommt \(f_M\) (also im Endeffekt die Maschine \(M\)) zwei Parameter übergeben: \(i\) und \(x\). Dabei geht \(f_M\) hin und berechnet die Funktion (welche auch immer) mit ihren zwei Argumenten \(i\) und \(x\). Was passiert, wenn wir im ersten Schritt nun \(i\) in unserer neuen Maschine \(M_i\) festsetzen?

Beispiel: \(f(i,x)=i+x\)

Um diese Funktion zu berechnen brauchen wir eine Maschine \(M\), die wir wie folgt definieren:

\(M=\{F,{\{1\}}^*\times {\{1\}}^*,{\{1\}}^*,EC^{(2)},AC\}\)

Die Eingabecodierung \(EC\) ist:

\(EC^{(2)}(1^i,^x)=(\epsilon,B,1^{i}B1^{x}B)\)

Konkretes Beispiel für \(f(2,3)\): \(EC^{(2)}(11,111)=(\epsilon,B,11B111B)\). Auf dem Eingabeband stehen also die Eingabeparameter \(i\) und \(x\) getrennt nebeneinander rechts vom Lesekopf.

Das dazugehörige Flussdiagramm \(F\) wäre:

Ausgeschrieben sieht das Flussdiagramm also so aus, nennen wir es mal \(\omega\in\Omega^{*}\):

\((0:1:1?,1,4)\)

\((1:1:R,2)\)

\((2:0:1,3)\)

\((3:0:R,0)\)

\((4:1:R,4)\)

\((5:1:1?,1,6)\)

\((6:HALT)\)

(Bitte nagelt mich nicht auf das Alphabet \(\Omega\) und den korrekten Aufbau der Befehle fest, mir geht es hier nur um das Verständnis)

Was tut es? Es geht Band \(1\) von Anfang bis Ende durch: findet es eine \(1\), so schreibt es auch eine \(1\) auf das Ausgabeband \(0\). Findet es ein erstes \(B\) (unser Trennzeichen zwischen dem Parameter \(1^i\) und \(1^x\)) auf dem Eingabeband \(1\), geht es auf dem Band nach rechts und schaut ob da der zweite Parameter steht. Bis zum nächsten \(B\), d.h. dem Ende des zweiten Parameters \(1 ^x\) wird nun in jedem Schritt eine weitere \(1\) auf das Ausgabeband \(0\) geschrieben.

PS: Ihr erinnert euch an das utm-Theorem und unsere \(h\)-Funktion? Wir können das ausgeschriebene Programm\(\omega\) (bzw. seine Gödelnummer \({\nu_{\Omega}}^{-1}(\omega)\)) und seine Eingaben auf Bänder unserer universellen Turingmaschine schreiben und es einfach simulieren. Behaltet das mal im Hinterkopf.

Am Ende haben wir also die Ausgabe \(f_M(1^i,1^x)=1^{f(i,x)}\)

Konkretes Beispiel: \(f_M(11,111)=1^5=11111\)

Und jetzt kommen wir zum Problem, das wir lösen wollen: wie schaffen wir es eine Maschine anzugeben, die nur einen Parameter \(1^x\) hat und dennoch das gleiche Resultat berechnet?

\(EC(1^x)=(\epsilon,B,1^i 1^xB)\)

Wie können wir denn \(1^i 1^x\) berechnen wenn wir gar kein \(1^i\) als Eingabeparameter haben?!

Ganz einfach: wir schreiben den Parameter \(1^i\) auf das Eingabeband, links neben \(1^x\) und rechnen dann wie \(M\) weiter. Nehmen wir wieder als konkrete Belegung \(i=1^2\) und lassen unser \(x\) variabel, was uns zu einer neuen Maschine \(M_2\) mit dem Flussdiagramm \(F_2\) führt:

Der grüne Teil ist der zusätzliche Part, ich nenne ihn mal \(\gamma_2\) (abhängig von \(i=2\)). Schreiben wir dieses komplette Flussdiagramm \(F_2\) aus, so haben wir \(\omega_2\) (Achtung, die Marken habe ich aus Faulheit nicht umbenannt. In Wirklichkeit müsste man sie umbenennen, so dass das neue Flussdiagramm \(F_2\) auch mit Marke \(0\) beginnt. Ich habe für die Marken vor Marke \(0\) einfach Buchstaben genommen) als Bandprogramm:

\((A:1:L,B)\)

\((B:1:1,C)\)

\((C:1:L,D)\)

\((D:1:1,E)\)

\((E:1:L,0)\)

\((0:1:1?,1,4)\)

\((1:1:R,2)\)

\((2:0:1,3)\)

\((3:0:R,0)\)

\((4:1:R,4)\)

\((5:1:1?,1,6)\)

\((6:HALT)\)

Nachdem der grüne Teil des Flussdiagramms \(\gamma_2\) ausgeführt wurde haben wir auf dem Eingabeband folgende Belegung:

\((\epsilon,B,1^{2}B1^{x}B)\).

Und, oh Wunder, das sieht ja genauso aus wir unsere Eingabecodierung für \(1^2,1^x\). Und schwupp, können wir ganz normal wie die ursprüngliche Maschine \(M\) (der weiße Teil im Flussdiagramm) weiterrechnen.

Wir Ihr euch leicht vorstellen könnt, können wir auch das für jedes beliebige \(i\) machen, indem wir den grünen Part \(\gamma\) einfach abhängig von \(i\) zu \(\gamma_i\) verlängern. Am Ende haben wir damit eine „Quasi-Eingangsbelegung“ von:

\((\epsilon,B,1^{i}B1^{x}B)\)

Abhängig von \(i\) haben wir somit immer eine neues Programm \(\omega_i\) mit der Maschine \(M_i\) inkl. – selbstverständlich – auch immer einer neuen Gödelnummer \(k={\nu_{\Omega}}^{-1}(\omega_i)\).

(Wiederholung: zur Funktion \(\nu_{\Omega}(k)\), welche uns zu einer Gödelnummer \(k\) das Bandprogramm \(\omega\) gibt, ist die Umkehrfunktion \({\nu_{\Omega}}^{-1}(\omega)\). Diese gibt uns zu einem Bandprogramm \(\omega\) die zugehörige Gödelnummer \(k\)).

Wir haben mit unserem Verfahren also das \(i\) innerhalb einer Maschine quasi „fixiert“. Mit der neuen Gödelnummer \(k\) können wir eine universelle Turingmaschine zu füttern und sie mit nur einem Parameter \(x\) simulieren, so dass gilt:

\(f(i,x) = \varphi_{r(i)}(x)\) für alle \(i,x \in \mathbb{N}\) bzw.

\(f_M(i,x)=r(f_M,i,x)=f_{M_i}(x)\)

Und das Problem? Tja… wir brauchen ein Verfahren, dass uns dieses Flussdiagramm \(F_i\) und damit auch das Bandprogramm \(\omega_i\) automatisch erzeugt und somit die Gödelnummer \(k={\nu_{\Omega}}^{-1}(\omega_i)\) abhängig von einem \(i\) berechnet. Dazu gehen wir wie folgt vor:

• Wir basteln uns eine Maschine \(N\), welche auf Band \(1\) den Parameter \(i\) hat
• \(N\) schreibt das komplette, initiale Programm \(\omega\) auf Band \(2\)
• Nun schreibt \(N\) den grünen Part, also das Teilprogramm (nennen wir es mal \(\gamma_i\), abhängig vom \(i\) auf Band \(3\)
• Nun kopiert \(N\) das initiale Programm \(\omega\) von Band \(2\) neben das Teilprogramm \(\gamma\) auf Band \(3\) und benennt die Marken so um, dass die erste Marke des Teilprogramms \(\gamma\) zuerst ausgeführt wird und anschließend in die erste Marke vom initialen Programm \(\omega\) mündet.

  Also praktisch genau das, was wir mit \(A-E\) gemacht haben, nur eben nicht so faul wie ich, sondern tatsächlich mit natürlichen Zahlen. Da das initiale Programm \(\omega\) auch mit der Marke \(0\) anfängt, müssen diese beim Kopiervorgang selbstverständlich auch umbenannt werden.

• Am Ende steht auf Band \(3\) also ein komplett neues Programm \(\omega_i\), dass wir interpretieren können.
• Der Vollständigkeit halber: da wir nicht den Code, sondern die Gödelnummer interpretieren, müssen wir \(\omega_i\) noch in die Gödelnummer umwandeln: \(k={\nu_{\Omega}}^{-1}(\omega_i)\)

Damit gilt \(f_N(1^i)=1^k\) und wir haben unser \(r\) gefunden:

\(r=\iota^{-1}(f_N(\iota(i)))\)

PS: \(\iota(i)=1^i\) und \(\iota^{-1}(1^i)=i\)

Schon wieder diese Iotas! Wollen wir das an dem obigen Beispiel mal durchspielen? Klar doch.

Beispiel: \(N\) für \(f(i,x)=i+x\)

Wir nutzen wieder unser \(M\) inkl. Flussdiagramm \(F\) von oben für die Berechnung der zweistelligen Funktion \(f\), sowie auch das ausgeschriebene Programm \(\omega\) davon.

• Mit der Maschine \(N\) und dem Programm \(\omega\) der initialen, zweistelligen Maschine \(M\) bekommen wir für \(f_N(1^i)=1^k\) die Gödelnummer von \(M_i\).
• \(r\) wäre dann:\(\begin{array}{ll}r(i)&={\iota}^{-1}(f_N({\iota}(i)))\\&={\iota}^{-1}(f_N(1^i))\\&={\iota}^{-1}(1^k)\\&=k\end{array}\)
• Damit haben wir zu einem \(i\) die Gödelnummer \(k\) einer Maschine, die uns zu jedem \(x\) die korrekte Funktion \(\varphi_k(x)=f(i,x)\) berechnet.

Konkretes Beispiel? Aber sicher!

Konkretes Beispiel: \(N\) für \(f(2,3)=2+3=5\)

Die Gödelnummern halte ich willkürlich, da die konkrete Berechnung ja nicht unbedingt wichtig ist. Tun wir also einfach so, als wäre die von \(N\) errechnete Gödelnummer von \(M_2\) einfach \(k=1^44\)

• \(N\) startet also mit \(i=2\) auf Band \(1\), schreibt das initiale Programm \(omega\) auf Band \(2\) und das Teilprogramm \(\gamma_2\) (grün) auf Band \(3\). Die Bänder von \(N\) sehen nun so aus (ich habe der Übersichtlichkeit halber (okay, ich gebe es zu, ich war wieder zu faul) nicht die ganzen Programme \(\omega\) und \(\gamma\) auf die Bänder gepackt):
• Jetzt geht \(N\) hin und kopiert das initiale Programm \(\omega\) von Band \(2\) links neben \(\omega\) auf Band \(2\) und benennt die Marken um (in unserem Beispiel sind die schon umbenannt – statt in Zahlen in Buchstaben, aber dennoch umbenannt -; normal würde das Teilprogramm auch mit \(0\) statt \(A\) starten usw.). Band \(3\) sieht dann so aus:

Leider ist die Grafik etwas klein geraten, Sorry. Am Ende steht also unser komplettes Programm \(\omega_2=\gamma_2\cdot\omega\) auf Band \(3\) mit umbenannten Marken, bereit zur Ausführung. Naja, fast bereit. Denn das Programm \(\omega_2\) selbst ist ja nicht ausführbar, sondern nur seine Gödelnummer.

• Und die bekommen wir, indem wir zum Programm \(\omega_2\) nun seine Gödelnummer \({\nu_{\Omega}}^{-1}(\omega_2)=1^44\) (nicht vergessen, \(1^44\) ist die willkürliche Gödelnummer für \(\omega_2\), die wir uns ausgedacht haben) berechnen. Wir wissen ja, dass wir durch die Ordnungsfunktion auf dem Alphabet unserer Bandprogramme auch eine Standardnummerierung haben.

  Die Funktion \({\nu_{\Omega}}^{-1}\) ist, wie wir im Beitrag zur Standardnummerierung gezeigt haben, berechenbar. Ich gebe hier also nicht extra ein Flussdiagramm einer Maschine an, dass uns zu den Zeichen des Programms \(\omega_2\) auf Band \(3\) anhand der Ordnungsfunktion die Gödelnummer berechnet. Wir könnten es aber problemlos.

Damit gilt letztendlich: \(f_N(11)=1^44\). Nur noch die \(1^44\) mit unseren Iotas (\(\iota\)) in Dezimaldarstellung umwandeln und wir sind fertig:

\(\begin{array}{ll}r(2)&=\iota^{-1}(f_N(\iota(2)))\\&=\iota^{-1}(f_N(1^2))\\&=\iota^{-1}(1^44))\\&=44\end{array}\)

Füttern wir die Maschine mit der Gödelnummer \(44\) \(M_2=\nu_M(\omega_2)\) nun mit unserem \(x=5\), so bekommen wir  \(f_{M_2}(2)=5\), was genau das gleiche ist wie \(f_M(2,3)=5\), das Ergebnis unserer Ursprungsmaschine \(M\) mit zwei Parametern.

Fertig.

Münzen wir das beispiel konkret auf das smn-Theorem, so bedeutet es:

\(f(2,3) = \varphi_{r(2)}(3)=\varphi_{144}(3)=5\) für \(i=2\) und \(x=3\) bzw.

\(f_M(2,3)=r(f_M,2,3)=f_{M_2}(3)=5\)

PS: nicht vergessen: \(f_M\) ist dabei unser Ursprungsprogramm \(\omega\), dass für \(N\) natürlich fest vorgegeben ist. Es ändert sich nicht, egal welches \(i\) oder \(x\) wir haben, daher können wir es für alle Eingaben fest vorgeben.

Und wenn Ihr nach oben, in die Definition vom smn-Theorem schaut, ist es genau die Definition, nur mit unseren Werten für \(i\) und \(x\) gefüllt.

Rekapitulieren wir: alles, was unser Programm \(r\) bzw. die Maschine \(N\) macht, ist uns ein festes Argument zusammen mit dem Quellcode des Urspungsprogramms in eine neue Maschine zu codieren und uns dazu die zugehörige Gödelnummer anzugeben. Mit unserer universellen Turingmaschine \(u_\varphi\) (utm-Theorem) können wir diese neue Maschine mit den verbliebenen, nicht fixierten Argumenten interpretieren. Nur der Zusammenhang zu \((S)\) ist euch wahrscheinlich noch nicht klar. Aber darum kümmern wir uns jetzt.

Die Eigenschaft \((S)\) (d.h. die effektive Komposition) gefordert wird. Wenn man also zwei Programme einer Sprache komponieren kann, ist das smn-Theorem erfüllt und umgekehrt. Das liegt an einer Kleinigkeit, unserer Funktion \(r\) aus dem smn-Theorem.

Zusammenhang zwischen effektiver Komposition und dem smn-Theorem

Wir schauen uns nochmal die Forderung (S) an, welche an Programmiersprachen gestellt wird:

• (S) Zu je zwei Programmen \(P\) und \(Q\) möchte man ein Programm für die Komposition konstruieren können, d.h. es soll eine berechenbare Funktion \(h\) geben, so dass \(\sigma(h(P,Q)=\sigma(Q) \circ\sigma(P)\).

Während die Funktion \(r\) in ihrer ursprünglichen Form, \(r: \mathbb{N} \rightarrow\mathbb{N}\) mit \(r(i) = k\) einen Index/Gödelnummer für eine neue Maschine ausgibt, damit \(f(i,x) = \varphi_k(x)\) gilt, gibt uns die gleiche Funktion, jedoch mit dem Definitionsbereich \(\mathbb{N}^2\), d.h.  \(r: \mathbb{N^2} \rightarrow\mathbb{N}\) (die Funktion \(r\) bekommt also zwei Parameter aus \(\mathbb{N}\) übergeben) auch nur einen Index einer Maschine. Dieses Mal jedoch den Index/Gödelnummer einer Maschine, die zwei Ursprungsmaschinen mit den Indizes \(i\) und \(j\) zusammenschaltet, so dass gilt:  \(f(<i,j>,x) = \varphi_i(\varphi_j(x))\). That’s it.

Funktionieren tut das genauso wie beim Beispiel zum smn-Theorem:

(Danke an Herbert für seinen Beitrag zum Thema in der NG)

• Dazu werden die Marken aus dem Flussdiagramm der Maschine \(i\) erhöht/umbenannt. Und zwar um den Wert der größten Marke aus dem Flussdiagramm der Maschine \(j\) damit es in der neuen Maschine keine gleichen Marken gibt, denn es könnte aus beiden Maschinen Marken mit der gleichen Nummer geben.
• Dann wird aus der \(HALT\)-Marke von Maschine \(i\) in die Startmarke der Maschine \(j\) und wir haben eine Zusammenschaltung und nur eine einzige Maschine aus zwei gebaut.
• Das können wir natürlich beliebig kombinieren, so dass unser \(r\) wie folgt definiert wird: \(r: \mathbb{N}^m \rightarrow\mathbb{N}\). Die „Übersetzungsleistung“ besteht hier nicht von einer Sprache in die andere, sondern in einer Zusammenschaltung von zwei Maschinen in eine durch Umbenennung der Marken und Verknüpfen der Flussdiagramme, so dass wir am Ende aus zwei Flussdiagrammen nur noch eines haben.

Wir können im Endeffekt also eine beliebige Anzahl (\(m\)) von Maschinen zusammenschalten, so dass wir am Ende nur eine Maschine haben. Jetzt können wir uns auch die übliche Definition der Funktion \(r\) herleiten, die normal \(s\) heißt:

\(s_n^{m}:\mathbb{N}^{m+1} \rightarrow \mathbb{N}\) mit \(\varphi_{s_n^{m}(i,y_1,…,y_m)}(z_1,…,z_n) = \varphi_i(y_1,…,y_m,z_1,…,z_n)\)

Und hier verstehen wir auch warum sich das Theorem eben smn-Theorem nennt. Die Funktion besagt nichts anderes, als dass wir \(m\) Maschinen zusammenschalten und somit in eine überführen/transformieren können, die mit \(n\) Argumenten gefüttert werden kann und das selbe Ergebnis hat wie die ursprüngliche Maschine. Und das ist ja genau unser Wunsch nach einer Komposition aus Forderung \((S)\).

Klar geworden? Damit haben wir nun auch unser \((S)\) abgehakt.

Antwort zum Lernziel: mit dem smn-Theorem ist es uns nicht nur möglich Eingabeparameter einer Maschine fest zu codieren und zur neu erzeugten Maschine eine Gödelnummer anzugeben, die um einen Eingabeparameter (den fest codierten) weniger benötigt und dennoch das gleiche Ergebnis berechnet (um Currying zu unterstützen), sondern wir können mit dem smn-Theorem auch Funktionen, d.h. Maschinen zusammenschalten um eine Forderung an gute Programmiersprachen zu erfüllen: (S) die Forderung nach einer effektiven Komposition.

Das funktioniert durch ein Zusammenfügen der Flussdiagramme, bzw. Befehle der Maschinen bei gleichzeitiger Umbenennung der Marken, so dass z.B. die \(HALT\)-Marke einer Maschine statt zu halten nun auf die Anfangsmarke der anderen Maschine verweist.

Zusammen mit dem utm-Theorem bilden sie das Grundgerüst für gute Programmiersprachen: (S) und (U).

Lernziel 6

Erläuterung des Äquivalenzsatzes für Nummerierungen (Rogers)

Wir machen uns zunächst klar, dass wir mit \(\varphi\) eine eigene Programmiersprache entwickelt haben. Wir konnten mit dieser alle Funktionen aus \(P^{(1)}\) nummerieren und diese auf unseren universellen Turingmaschinen ausführen.

Zwar haben wir die Syntax und die Notation dieser Bandbefehle willkürlich gewählt. Das ist aber gar nicht tragisch, denn die Nummerierung im Skript ist genauso gut wie jede andere. Vorausgesetzt sie erfüllt das utm- (universelle Turingmaschine) und das smn- (Übersetzungslemma) Theorem. Dann sind die Nummerierungen nämlich äquivalent zueinander, da sie ineinander überführbar sind.

Der Äquivalenzsatz von Rogers besagt formal:

Sei \(\psi\) eine Nummerierung von \(P^{(1)}\), dann sind folgende Eigenschaften äquivalent:

1. \(\psi \equiv \varphi\)

2. \(\psi\) erfüllt das utm- (universelle Funktion von \(\psi\) ist berechenbar) und das smn- (Berechnung der Nummer eines Programms und damit z.B. die Übersetzung in eine andere Programmiersprache) Theorem.

Damit lassen sich alle Programme, die beide Theoreme erfüllen durch „Übersetzer“ \(g,h\in R^{(1)}\) ineinander übersetzen. D.h. soviel wie:

\(\varphi=g(\psi)\) und

\(\psi=h(\varphi)\).

Wir können uns daher auf eine Nummerierung beschränken wenn sie die beiden Theoreme erfüllt. Unser \(\varphi\) ist somit genauso gut wie jede andere Nummerierung (die natürlich auch das utm- und das smn-Theorem erfüllen muss).

Antwort zum Lernziel: nach dem Äquivalenzsatz von Rogers sind alle Programmiersprachen/Nummerierungen äquivalent wenn sie das utm- und das smn-Theorem erfüllen.

Hat man also eine andere Programmiersprache/Nummerierung \(\psi:\mathbb{N}\rightarrow P^{(1)}\), die beide Theoreme erfüllt, so sind diese äquivalent, d.h. \(\varphi\equiv\psi\) und können mit „Übersetzern“ ineinander überführt werden.

Lernziel 7

Formulieren des Rekursionssatzes

Dieser Satz wird auch Fixpunktsatz von Kleene genannt. Ich fand es persönlich einfacher von der anderen Seite an diesen Satz heranzugehen, die Skripte der HU Berlin gehen einen ähnlichen weg. Aber fangen wir mal an: ein schönes Beispiel für den Rekursionssatz ist die Selbstreproduktion. Wir wollen also ein Programm, dass bei einer beliebigen Eingabe sich selbst ausgibt. Dazu ist der Rekursionssatz hilfreich.

Formal ausgedrückt:

Zu jeder Funktion \(f \in R^{(1)}\) gibt es eine Zahl \(n\) mit \(\varphi_n = \varphi_{f(n)}\).

Was bedeutet das nun genau und was ist \(n\)? \(n\) ist die Gödelnummer einer Maschine, also quasi unser in natürliche Zahlen codierter Programmcode (kennt Ihr schon, Thema Standardnummerierung). Unsere Programmtransformationsfunktion \(f\) bekommt als Eingabe diese Gödelnummer \(n\), rechnet darauf rum und gibt uns als Ausgabe eine Gödelnummer \(f(n)=k\) aus.

Wenn wir nun die Maschine mit der Gödelnummer \(k\) und dem Parameter \(x\) starten (\(\varphi_k(x)\)), so bekommen wie die gleiche Ausgabe, die unser Programm mit der Gödelnummer \(n\) und dem Parameter \(x\) gehabt hätte (\(\varphi_n(x)\)), d.h.

\(\varphi_n(x) = \varphi_{f(n)}(x)\)

Umgangssprachlich gesprochen: Wir können \(f\) als eine „Programmumschreibefunktion“ betrachten. Nach diesem Satz gibt es Programme, die in ihrer Funktion von unserer Programmtransformationsfunktion \(f\) nicht verändert werden. Aber Achtung: nur in der Funktion, d.h. es könnten Programmteile abgeändert oder hinzugefügt werden, die nicht zur Ausführung kommen. Die korrekte und gleiche Funktion/Ausgabe des Programms ist damit dennoch gegeben.

\(n\) wird deswegen auch der semantische Fixpunkt der Modifikationsfunktion \(f\) genannt.

Damit ist es uns z.B. erlaubt Maschinen zu erstellen, welche eine Beschreibung von sich selbst berechnen und benutzen können. Das ist keineswegs selbstverständlich! Denn lange Zeit galt diese sog. Selbstreproduktion, d.h. Maschinen, die sich selbst nachbauen ohne sich selbst zu enthalten als unmöglich.

Alle Erfindungen, die andere Dinge herstellten wie z.B. eine Autofabrik oder Werkzeughersteller sind komplexer als das erzeugte Produkt und brauchen eine Beschreibung des herzustellenden Produktes. Damit wäre die Selbstreproduktion aber unmöglich, denn um einfache Produkte zu bauen, braucht man komplexe.

Und genau das ist der Trugschluss, den von Neumann 1966 aufgezeigt hat, indem er theoretisch eine einfache Maschine konstruierte, die sich selbst reproduzieren kann:

Diese Maschine besteht aus drei Teilen:

• dem Konstrukteur \(K\)

  Der Konstrukteur bekommt die Beschreibung einer Maschine (mathematisch gesehen also z.B. unsere Gödelnummer \(i\)) und setzt diese dann mit den Bauteilen zusammen, so dass wir eine Maschine mit \(\varphi_i\) bekommen.

• dem Kopierer \(C\)

  Der Kopierer kann den Bandinhalt von einem Band auf ein anderes kopieren, so dass am Ende zwei Bänder mit dem selben Inhalt als Ausgabe ausgegeben werden.

• der Steuerung \(S\)

  Die Steuerung kümmert such um Konstrukteur und Kopierer und versorgt beide mit Eingaben.

Was wir also brauchen ist, eine Maschine \(M\), die bei der Eingabe von sich selbst, sich selbst reproduziert. Und so sieht dann die Maschine aus:

Wir geben den Bauplan \(i\) in die Steuerung, diese gibt sie an den Kopierer, welcher den Bauplan verdoppelt. Eine Kopie wird an den Konstrukteur übergeben, der daraus eine neue Maschine \(M_i\) baut. Und eben diese neue Maschine (der „Sohn“) bekommt dann von seinem „Vater“ den Bauplan ausgehändigt und baut dann den „Enkel“, eine exakte Kopie von sich selbst usw.

Und nun wieder zurück zur theoretischen Informatik:

Wir haben damit eine Möglichkeit zur Selbstreproduktion und können Maschinen angeben, die sich selbst ausgeben können. Mit dem Rekursionssatz ist es also sichergestellt, dass es ein Programm gibt, welches bei allen möglichen Eingaben sich selbst ausgibt. Eine Anwendung sind z.B. die Quines, denn sie geben bei jeder Ausgabe sich selbst aus, damit gilt der Satz über Selbstreproduktion:

Es gibt eine Zahl \(n\), so dass \(\varphi_n(x) = n\) für alle \(x\).

Wer könnte denn an sowas interessiert sein? Außer Skynet. Viren zu Beispiel.

Just als ich den Beitrag getippt habe, fliegt mir ein Satz Folien um die Ohren, die ich euch nicht vorenthalten will: Folien zur Selbstreproduktion der Uni Potsdam.

Antwort zum Lernziel: Der Rekursionssatz von Kleene besagt, dass man zu einem gegebenen Modifikationsprogramm \(f\) immer einen Quelltext finden kann, der trotz Modifikation seine Aufgabe weiterhin erfüllt. Da sich die Semantik des Programms somit nicht ändert wird dieser Quelltext (das \(n\)) auch semantischer Fixpunkt von \(f\) genannt.

Ein Anwendungsbereich dieses Satzes ist die Selbstreproduktion, so dass die Ausgabe von sich selbst der Fixpunkt ist (das Programm gibt sich selbst aus) und es gelten muss: \(\varphi_n(x)=n\), egal was man als \(x\) eingibt.

Puh, das war ein Haufen arbeit. Wie immer gilt: sollten sich Fehler eingeschlichen haben: bitte wieder Bescheid geben. Danke auch an die Kollegen aus der NG, die so manche einleuchtende Erklärung eingeworfen und zu diesem Text beigetragen haben. Schade, dass die NG jedes Semester gelöscht wird. So verwindet manch eine schöne Erläuterung im digitalen Papierkorb. Vielleicht trägt der Blog ja etwas dazu bei, dass einige Erläuterungen über das Haltbarkeitsdatum der NG bestehen bleiben.