TIA: smn-Theorem, Rekursions- und Äquivalenzsatz (Lernziele KE5, 3/3)

Update: Formulierungen etwas verständlicher gemacht. Wenn euch das smn-Theorem noch nicht ganz klar, war bitte den Beitrag nochmal lesen.

Update: aus zwei macht drei. Das ist nun hoffentlich der letzte Teil zu KE5 mit einem riesen Beispiel zum smn-Theorem.

Noch einmal die Wiederholung der zwei Anforderungen an vernünftige Programmiersprachen:

• (U) Es soll einen Computer geben, der zu jedem Programm $P$ und jedem möglichen Eingabewert $x$ das Resultat $\sigma(P)(x)$ berechnet und nicht hält wenn $\sigma(P)(x)$ nicht existiert.
• (S) Zu je zwei Programmen $P$ und $Q$ möchte man ein Programm für die Komposition konstruieren können, d.h. es soll eine berechenbare Funktion $h$ geben, so dass $\sigma(h(P,Q)=\sigma(Q) \circ\sigma(P)$.

Während wir (U) mit dem utm-Theorem gut behandeln konnten, schauen wir uns jetzt (S) an:

Lernziel 5

Erklärung und Anwendung des smn-Theorems

Kommen wir nun zum smn-Theorem, unserem Übersetzungslemma. Formal ausgedrückt:

$f \in P^{(2)}$, dann gibt es eine total-rekursive Funktion $r \in R^{(1)}$ mit:

$f(i,j) = \varphi_{r(i)}(j)$ für alle $i,j \in \mathbb{N}$.

Ehm, ja. Was macht das Ding nun?

Im wesentlichen geht es darum, dass sich berechenbare Funktionen kombinieren lassen. Durch die Hintereinanderausführung lassen sich neue Funktionen und somit auch neue Programme (und damit selbstverständlich auch neue Maschinen) mit eigenen Gödelnummern $i$ erschaffen.

Dazu werden die Funktionen einfach hintereinander ausgeführt und die Variable $x$ als Eingabe immer wieder von Maschine zu Maschine "mitgenommen". Da bei diesem Vorgang, abhängig von der konkreten Belegung der Variable $x$ eine neue Maschine erschaffen wird, gibt uns unsere Funktion $r$ diese neue Gödelnummer preis. In dieser Maschine ist die Variable $x$ konkret belegt und fixiert. Variable $j$ nimmt sie jedoch ganz normal an.

Dadurch ist es möglich aus Funktionen mit mehreren Argumenten Funktionen mit nur einem Argument zu erstellen, die jedoch das selbe berechnen (Currying genannt). Wir "fixieren" sozusagen Argumente und codieren sie in unsere neuen Maschinen ein. Am Beispiel unten wird es etwas deutlicher.

Zunächst: $R^{(1)}$ sind die berechenbaren, totalen, einstelligen Funktionen (sie sind überall in $\mathbb{N}$ definiert). Die Funktionen in $P^{(1)}$ müssen nicht überall definiert sein. Im Skript ist das in menschlicher Sprache beschrieben:

"Jedes Programm der Programmiersprache $\psi$ für Zahlenfunktionen mit berechenbarer, universeller Funktion kann mit der Funktion $r$ in die Programmiersprache $\varphi$ übersetzt werden"

Das trifft es eig. ganz gut. Das ist jedoch nicht direkt die Formalisierung unseres $(S)$, der Zusammenhang kommt aber gleich noch.

In der Wikipedia steht zum smn-Theorem auch noch folgender Satz (den ich leicht modifiziert habe damit er besser zu uns passt):

"Die smn - Eigenschaft besagt, dass es zu einem Code $f_M$, der mit den Parametern $i$ und $x$ ausgeführt wird (bzw. ausgeführt werden kann), ein Transformationsprogramm $r$ gibt, das aus $f_M$, $i$ und $x$ ein Programm $f_{M_i}$ berechnet, welches bei der Eingabe von $x$ das gleiche berechnet, wie $f_M$ bei der Eingabe von $i$ und $x$"

Ja, macht Sinn. Formal ausgedrückt:

$f_M(i,x)=r(f_M,i,x)=f_{M_i}(x)$

(Hier sind $i$ und $x$ Argumente, und $f_M$ die Gödelnummer der Ursprungsmaschine, $f_{M_i}$ ist dann die Gödelnummer der Maschine mit dem festgesetzten $i$).

Auch ist es nicht das eig. smn-Theorem, welches sonst überall verwendet wird und die Stelligkeit $m + n$ nutzt, sondern eine abgewandelte Form davon (wie vieles andere im Skript auch), damit es für den Leser nicht zu einfach wird und er Zusatzliteratur heranziehen kann. Wo kämen wir denn hin?!

Als Beweis im Skript wird folgende Idee angebracht:

Zunächst machen wir uns klar, was wir suchen. Wir brauchen eine Maschine für unsere Funktion $r$ aus der Definition.

Wir wir oben sehen, bekommt $f_M$ (also im Endeffekt die Maschine $M$) zwei Parameter übergeben: $i$ und $x$. Dabei geht $f_M$ hin und berechnet die Funktion (welche auch immer) mit ihren zwei Argumenten $i$ und $x$. Was passiert, wenn wir im ersten Schritt nun $i$ in unserer neuen Maschine $M_i$ festsetzen?

Beispiel: $f(i,x)=i+x$

Um diese Funktion zu berechnen brauchen wir eine Maschine $M$, die wir wie folgt definieren:

$M=\{F,{\{1\}}^*\times {\{1\}}^*,{\{1\}}^*,EC^{(2)},AC\}$

Die Eingabecodierung $EC$ ist:

$EC^{(2)}(1^i,^x)=(\epsilon,B,1^{i}B1^{x}B)$

Konkretes Beispiel für $f(2,3)$: $EC^{(2)}(11,111)=(\epsilon,B,11B111B)$. Auf dem Eingabeband stehen also die Eingabeparameter $i$ und $x$ getrennt nebeneinander rechts vom Lesekopf.

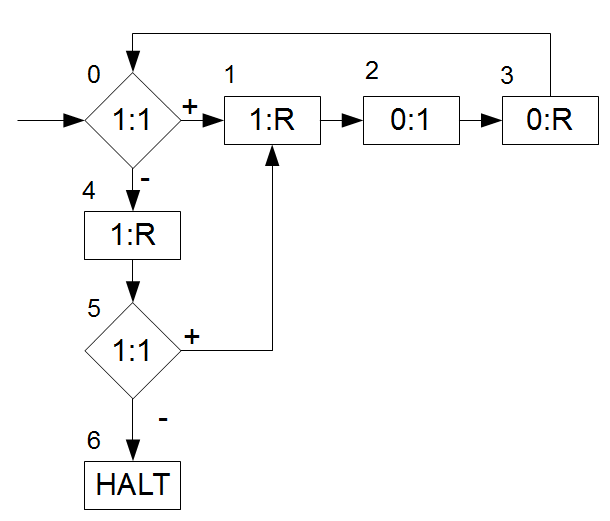
Das dazugehörige Flussdiagramm $F$ wäre:

Ausgeschrieben sieht das Flussdiagramm also so aus, nennen wir es mal $\omega\in\Omega^{*}$:

$(0:1:1?,1,4)$

$(1:1:R,2)$

$(2:0:1,3)$

$(3:0:R,0)$

$(4:1:R,4)$

$(5:1:1?,1,6)$

$(6:HALT)$

(Bitte nagelt mich nicht auf das Alphabet $\Omega$ und den korrekten Aufbau der Befehle fest, mir geht es hier nur um das Verständnis)

Was tut es? Es geht Band $1$ von Anfang bis Ende durch: findet es eine $1$, so schreibt es auch eine $1$ auf das Ausgabeband $0$. Findet es ein erstes $B$ (unser Trennzeichen zwischen dem Parameter $1^i$ und $1^x$) auf dem Eingabeband $1$, geht es auf dem Band nach rechts und schaut ob da der zweite Parameter steht. Bis zum nächsten $B$, d.h. dem Ende des zweiten Parameters $1 ^x$ wird nun in jedem Schritt eine weitere $1$ auf das Ausgabeband $0$ geschrieben.

PS: Ihr erinnert euch an das utm-Theorem und unsere $h$-Funktion? Wir können das ausgeschriebene Programm$\omega$ (bzw. seine Gödelnummer ${\nu_{\Omega}}^{-1}(\omega)$) und seine Eingaben auf Bänder unserer universellen Turingmaschine schreiben und es einfach simulieren. Behaltet das mal im Hinterkopf.

Am Ende haben wir also die Ausgabe $f_M(1^i,1^x)=1^{f(i,x)}$

Konkretes Beispiel: $f_M(11,111)=1^5=11111$

Und jetzt kommen wir zum Problem, das wir lösen wollen: wie schaffen wir es eine Maschine anzugeben, die nur einen Parameter $1^x$ hat und dennoch das gleiche Resultat berechnet?

$EC(1^x)=(\epsilon,B,1^i 1^xB)$

Wie können wir denn $1^i 1^x$ berechnen wenn wir gar kein $1^i$ als Eingabeparameter haben?!

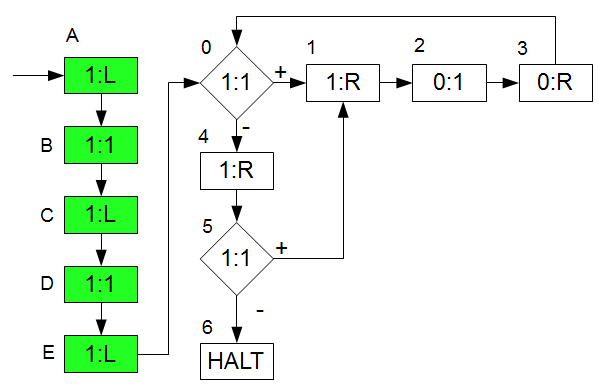
Ganz einfach: wir schreiben den Parameter $1^i$ auf das Eingabeband, links neben $1^x$ und rechnen dann wie $M$ weiter. Nehmen wir wieder als konkrete Belegung $i=1^2$ und lassen unser $x$ variabel, was uns zu einer neuen Maschine $M_2$ mit dem Flussdiagramm $F_2$ führt:

Der grüne Teil ist der zusätzliche Part, ich nenne ihn mal $\gamma_2$ (abhängig von $i=2$). Schreiben wir dieses komplette Flussdiagramm $F_2$ aus, so haben wir $\omega_2$ (Achtung, die Marken habe ich aus Faulheit nicht umbenannt. In Wirklichkeit müsste man sie umbenennen, so dass das neue Flussdiagramm $F_2$ auch mit Marke $0$ beginnt. Ich habe für die Marken vor Marke $0$ einfach Buchstaben genommen) als Bandprogramm:

$(A:1:L,B)$

$(B:1:1,C)$

$(C:1:L,D)$

$(D:1:1,E)$

$(E:1:L,0)$

$(0:1:1?,1,4)$

$(1:1:R,2)$

$(2:0:1,3)$

$(3:0:R,0)$

$(4:1:R,4)$

$(5:1:1?,1,6)$

$(6:HALT)$

Nachdem der grüne Teil des Flussdiagramms $\gamma_2$ ausgeführt wurde haben wir auf dem Eingabeband folgende Belegung:

$(\epsilon,B,1^{2}B1^{x}B)$.

Und, oh Wunder, das sieht ja genauso aus wir unsere Eingabecodierung für $1^2,1^x$. Und schwupp, können wir ganz normal wie die ursprüngliche Maschine $M$ (der weiße Teil im Flussdiagramm) weiterrechnen.

Wir Ihr euch leicht vorstellen könnt, können wir auch das für jedes beliebige $i$ machen, indem wir den grünen Part $\gamma$ einfach abhängig von $i$ zu $\gamma_i$ verlängern. Am Ende haben wir damit eine "Quasi-Eingangsbelegung" von:

$(\epsilon,B,1^{i}B1^{x}B)$

Abhängig von $i$ haben wir somit immer eine neues Programm $\omega_i$ mit der Maschine $M_i$ inkl. - selbstverständlich - auch immer einer neuen Gödelnummer $k={\nu_{\Omega}}^{-1}(\omega_i)$.

(Wiederholung: zur Funktion $\nu_{\Omega}(k)$, welche uns zu einer Gödelnummer $k$ das Bandprogramm $\omega$ gibt, ist die Umkehrfunktion ${\nu_{\Omega}}^{-1}(\omega)$. Diese gibt uns zu einem Bandprogramm $\omega$ die zugehörige Gödelnummer $k$).

Wir haben mit unserem Verfahren also das $i$ innerhalb einer Maschine quasi "fixiert". Mit der neuen Gödelnummer $k$ können wir eine universelle Turingmaschine zu füttern und sie mit nur einem Parameter $x$ simulieren, so dass gilt:

$f(i,x) = \varphi_{r(i)}(x)$ für alle $i,x \in \mathbb{N}$ bzw.

$f_M(i,x)=r(f_M,i,x)=f_{M_i}(x)$

Und das Problem? Tja... wir brauchen ein Verfahren, dass uns dieses Flussdiagramm $F_i$ und damit auch das Bandprogramm $\omega_i$ automatisch erzeugt und somit die Gödelnummer $k={\nu_{\Omega}}^{-1}(\omega_i)$ abhängig von einem $i$ berechnet. Dazu gehen wir wie folgt vor:

• Wir basteln uns eine Maschine $N$, welche auf Band $1$ den Parameter $i$ hat
• $N$ schreibt das komplette, initiale Programm $\omega$ auf Band $2$
• Nun schreibt $N$ den grünen Part, also das Teilprogramm (nennen wir es mal $\gamma_i$, abhängig vom $i$ auf Band $3$
• Nun kopiert $N$ das initiale Programm $\omega$ von Band $2$ neben das Teilprogramm $\gamma$ auf Band $3$ und benennt die Marken so um, dass die erste Marke des Teilprogramms $\gamma$ zuerst ausgeführt wird und anschließend in die erste Marke vom initialen Programm $\omega$ mündet.
  Also praktisch genau das, was wir mit $A-E$ gemacht haben, nur eben nicht so faul wie ich, sondern tatsächlich mit natürlichen Zahlen. Da das initiale Programm $\omega$ auch mit der Marke $0$ anfängt, müssen diese beim Kopiervorgang selbstverständlich auch umbenannt werden.
• Am Ende steht auf Band $3$ also ein komplett neues Programm $\omega_i$, dass wir interpretieren können.
• Der Vollständigkeit halber: da wir nicht den Code, sondern die Gödelnummer interpretieren, müssen wir $\omega_i$ noch in die Gödelnummer umwandeln: $k={\nu_{\Omega}}^{-1}(\omega_i)$

Damit gilt $f_N(1^i)=1^k$ und wir haben unser $r$ gefunden:

$r=\iota^{-1}(f_N(\iota(i)))$

PS: $\iota(i)=1^i$ und $\iota^{-1}(1^i)=i$

Schon wieder diese Iotas! Wollen wir das an dem obigen Beispiel mal durchspielen? Klar doch.

Beispiel: $N$ für $f(i,x)=i+x$

Wir nutzen wieder unser $M$ inkl. Flussdiagramm $F$ von oben für die Berechnung der zweistelligen Funktion $f$, sowie auch das ausgeschriebene Programm $\omega$ davon.

• Mit der Maschine $N$ und dem Programm $\omega$ der initialen, zweistelligen Maschine $M$ bekommen wir für $f_N(1^i)=1^k$ die Gödelnummer von $M_i$.
• $r$ wäre dann:$\begin{array}{ll}r(i)&={\iota}^{-1}(f_N({\iota}(i)))\\&={\iota}^{-1}(f_N(1^i))\\&={\iota}^{-1}(1^k)\\&=k\end{array}$
• Damit haben wir zu einem $i$ die Gödelnummer $k$ einer Maschine, die uns zu jedem $x$ die korrekte Funktion $\varphi_k(x)=f(i,x)$ berechnet.

Konkretes Beispiel? Aber sicher!

Konkretes Beispiel: $N$ für $f(2,3)=2+3=5$

Die Gödelnummern halte ich willkürlich, da die konkrete Berechnung ja nicht unbedingt wichtig ist. Tun wir also einfach so, als wäre die von $N$ errechnete Gödelnummer von $M_2$ einfach $k=1^44$

• $N$ startet also mit $i=2$ auf Band $1$, schreibt das initiale Programm $omega$ auf Band $2$ und das Teilprogramm $\gamma_2$ (grün) auf Band $3$. Die Bänder von $N$ sehen nun so aus (ich habe der Übersichtlichkeit halber (okay, ich gebe es zu, ich war wieder zu faul) nicht die ganzen Programme $\omega$ und $\gamma$ auf die Bänder gepackt):
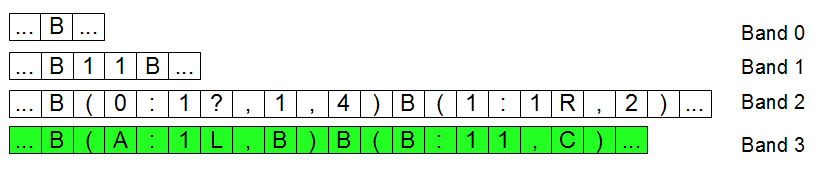
• Jetzt geht $N$ hin und kopiert das initiale Programm $\omega$ von Band $2$ links neben $\omega$ auf Band $2$ und benennt die Marken um (in unserem Beispiel sind die schon umbenannt - statt in Zahlen in Buchstaben, aber dennoch umbenannt -; normal würde das Teilprogramm auch mit $0$ statt $A$ starten usw.). Band $3$ sieht dann so aus:

Leider ist die Grafik etwas klein geraten, Sorry. Am Ende steht also unser komplettes Programm $\omega_2=\gamma_2\cdot\omega$ auf Band $3$ mit umbenannten Marken, bereit zur Ausführung. Naja, fast bereit. Denn das Programm $\omega_2$ selbst ist ja nicht ausführbar, sondern nur seine Gödelnummer.

• Und die bekommen wir, indem wir zum Programm $\omega_2$ nun seine Gödelnummer ${\nu_{\Omega}}^{-1}(\omega_2)=1^44$ (nicht vergessen, $1^44$ ist die willkürliche Gödelnummer für $\omega_2$, die wir uns ausgedacht haben) berechnen. Wir wissen ja, dass wir durch die Ordnungsfunktion auf dem Alphabet unserer Bandprogramme auch eine Standardnummerierung haben.
  Die Funktion ${\nu_{\Omega}}^{-1}$ ist, wie wir im Beitrag zur Standardnummerierung gezeigt haben, berechenbar. Ich gebe hier also nicht extra ein Flussdiagramm einer Maschine an, dass uns zu den Zeichen des Programms $\omega_2$ auf Band $3$ anhand der Ordnungsfunktion die Gödelnummer berechnet. Wir könnten es aber problemlos.

Damit gilt letztendlich: $f_N(11)=1^44$. Nur noch die $1^44$ mit unseren Iotas ($\iota$) in Dezimaldarstellung umwandeln und wir sind fertig:

$\begin{array}{ll}r(2)&=\iota^{-1}(f_N(\iota(2)))\\&=\iota^{-1}(f_N(1^2))\\&=\iota^{-1}(1^44))\\&=44\end{array}$

Füttern wir die Maschine mit der Gödelnummer $44$ $M_2=\nu_M(\omega_2)$ nun mit unserem $x=5$, so bekommen wir  $f_{M_2}(2)=5$, was genau das gleiche ist wie $f_M(2,3)=5$, das Ergebnis unserer Ursprungsmaschine $M$ mit zwei Parametern.

Fertig.

Münzen wir das beispiel konkret auf das smn-Theorem, so bedeutet es:

$f(2,3) = \varphi_{r(2)}(3)=\varphi_{144}(3)=5$ für $i=2$ und $x=3$ bzw.

$f_M(2,3)=r(f_M,2,3)=f_{M_2}(3)=5$

PS: nicht vergessen: $f_M$ ist dabei unser Ursprungsprogramm $\omega$, dass für $N$ natürlich fest vorgegeben ist. Es ändert sich nicht, egal welches $i$ oder $x$ wir haben, daher können wir es für alle Eingaben fest vorgeben.

Und wenn Ihr nach oben, in die Definition vom smn-Theorem schaut, ist es genau die Definition, nur mit unseren Werten für $i$ und $x$ gefüllt.

Rekapitulieren wir: alles, was unser Programm $r$ bzw. die Maschine $N$ macht, ist uns ein festes Argument zusammen mit dem Quellcode des Urspungsprogramms in eine neue Maschine zu codieren und uns dazu die zugehörige Gödelnummer anzugeben. Mit unserer universellen Turingmaschine $u_\varphi$ (utm-Theorem) können wir diese neue Maschine mit den verbliebenen, nicht fixierten Argumenten interpretieren. Nur der Zusammenhang zu $(S)$ ist euch wahrscheinlich noch nicht klar. Aber darum kümmern wir uns jetzt.

Die Eigenschaft $(S)$ (d.h. die effektive Komposition) gefordert wird. Wenn man also zwei Programme einer Sprache komponieren kann, ist das smn-Theorem erfüllt und umgekehrt. Das liegt an einer Kleinigkeit, unserer Funktion $r$ aus dem smn-Theorem.

Zusammenhang zwischen effektiver Komposition und dem smn-Theorem

Wir schauen uns nochmal die Forderung (S) an, welche an Programmiersprachen gestellt wird:

• (S) Zu je zwei Programmen $P$ und $Q$ möchte man ein Programm für die Komposition konstruieren können, d.h. es soll eine berechenbare Funktion $h$ geben, so dass $\sigma(h(P,Q)=\sigma(Q) \circ\sigma(P)$.

Während die Funktion $r$ in ihrer ursprünglichen Form, $r: \mathbb{N} \rightarrow\mathbb{N}$ mit $r(i) = k$ einen Index/Gödelnummer für eine neue Maschine ausgibt, damit $f(i,x) = \varphi_k(x)$ gilt, gibt uns die gleiche Funktion, jedoch mit dem Definitionsbereich $\mathbb{N}^2$, d.h.  $r: \mathbb{N^2} \rightarrow\mathbb{N}$ (die Funktion $r$ bekommt also zwei Parameter aus $\mathbb{N}$ übergeben) auch nur einen Index einer Maschine. Dieses Mal jedoch den Index/Gödelnummer einer Maschine, die zwei Ursprungsmaschinen mit den Indizes $i$ und $j$ zusammenschaltet, so dass gilt:  $f(<i,j>,x) = \varphi_i(\varphi_j(x))$. That's it.

Funktionieren tut das genauso wie beim Beispiel zum smn-Theorem:

(Danke an Herbert für seinen Beitrag zum Thema in der NG)

• Dazu werden die Marken aus dem Flussdiagramm der Maschine $i$ erhöht/umbenannt. Und zwar um den Wert der größten Marke aus dem Flussdiagramm der Maschine $j$ damit es in der neuen Maschine keine gleichen Marken gibt, denn es könnte aus beiden Maschinen Marken mit der gleichen Nummer geben.
• Dann wird aus der $HALT$-Marke von Maschine $i$ in die Startmarke der Maschine $j$ und wir haben eine Zusammenschaltung und nur eine einzige Maschine aus zwei gebaut.
• Das können wir natürlich beliebig kombinieren, so dass unser $r$ wie folgt definiert wird: $r: \mathbb{N}^m \rightarrow\mathbb{N}$. Die "Übersetzungsleistung" besteht hier nicht von einer Sprache in die andere, sondern in einer Zusammenschaltung von zwei Maschinen in eine durch Umbenennung der Marken und Verknüpfen der Flussdiagramme, so dass wir am Ende aus zwei Flussdiagrammen nur noch eines haben.

Wir können im Endeffekt also eine beliebige Anzahl ($m$) von Maschinen zusammenschalten, so dass wir am Ende nur eine Maschine haben. Jetzt können wir uns auch die übliche Definition der Funktion $r$ herleiten, die normal $s$ heißt:

$s_n^{m}:\mathbb{N}^{m+1} \rightarrow \mathbb{N}$ mit $\varphi_{s_n^{m}(i,y_1,...,y_m)}(z_1,...,z_n) = \varphi_i(y_1,...,y_m,z_1,...,z_n)$

Und hier verstehen wir auch warum sich das Theorem eben smn-Theorem nennt. Die Funktion besagt nichts anderes, als dass wir $m$ Maschinen zusammenschalten und somit in eine überführen/transformieren können, die mit $n$ Argumenten gefüttert werden kann und das selbe Ergebnis hat wie die ursprüngliche Maschine. Und das ist ja genau unser Wunsch nach einer Komposition aus Forderung $(S)$.

Klar geworden? Damit haben wir nun auch unser $(S)$ abgehakt.

Antwort zum Lernziel: mit dem smn-Theorem ist es uns nicht nur möglich Eingabeparameter einer Maschine fest zu codieren und zur neu erzeugten Maschine eine Gödelnummer anzugeben, die um einen Eingabeparameter (den fest codierten) weniger benötigt und dennoch das gleiche Ergebnis berechnet (um Currying zu unterstützen), sondern wir können mit dem smn-Theorem auch Funktionen, d.h. Maschinen zusammenschalten um eine Forderung an gute Programmiersprachen zu erfüllen: (S) die Forderung nach einer effektiven Komposition.

Das funktioniert durch ein Zusammenfügen der Flussdiagramme, bzw. Befehle der Maschinen bei gleichzeitiger Umbenennung der Marken, so dass z.B. die $HALT$-Marke einer Maschine statt zu halten nun auf die Anfangsmarke der anderen Maschine verweist.

Zusammen mit dem utm-Theorem bilden sie das Grundgerüst für gute Programmiersprachen: (S) und (U).

Lernziel 6

Erläuterung des Äquivalenzsatzes für Nummerierungen (Rogers)

Wir machen uns zunächst klar, dass wir mit $\varphi$ eine eigene Programmiersprache entwickelt haben. Wir konnten mit dieser alle Funktionen aus $P^{(1)}$ nummerieren und diese auf unseren universellen Turingmaschinen ausführen.

Zwar haben wir die Syntax und die Notation dieser Bandbefehle willkürlich gewählt. Das ist aber gar nicht tragisch, denn die Nummerierung im Skript ist genauso gut wie jede andere. Vorausgesetzt sie erfüllt das utm- (universelle Turingmaschine) und das smn- (Übersetzungslemma) Theorem. Dann sind die Nummerierungen nämlich äquivalent zueinander, da sie ineinander überführbar sind.

Der Äquivalenzsatz von Rogers besagt formal:

Sei $\psi$ eine Nummerierung von $P^{(1)}$, dann sind folgende Eigenschaften äquivalent:

1. $\psi \equiv \varphi$

2. $\psi$ erfüllt das utm- (universelle Funktion von $\psi$ ist berechenbar) und das smn- (Berechnung der Nummer eines Programms und damit z.B. die Übersetzung in eine andere Programmiersprache) Theorem.

Damit lassen sich alle Programme, die beide Theoreme erfüllen durch "Übersetzer" $g,h\in R^{(1)}$ ineinander übersetzen. D.h. soviel wie:

$\varphi=g(\psi)$ und

$\psi=h(\varphi)$.

Wir können uns daher auf eine Nummerierung beschränken wenn sie die beiden Theoreme erfüllt. Unser $\varphi$ ist somit genauso gut wie jede andere Nummerierung (die natürlich auch das utm- und das smn-Theorem erfüllen muss).

Antwort zum Lernziel: nach dem Äquivalenzsatz von Rogers sind alle Programmiersprachen/Nummerierungen äquivalent wenn sie das utm- und das smn-Theorem erfüllen.

Hat man also eine andere Programmiersprache/Nummerierung $\psi:\mathbb{N}\rightarrow P^{(1)}$, die beide Theoreme erfüllt, so sind diese äquivalent, d.h. $\varphi\equiv\psi$ und können mit "Übersetzern" ineinander überführt werden.

Lernziel 7

Formulieren des Rekursionssatzes

Dieser Satz wird auch Fixpunktsatz von Kleene genannt. Ich fand es persönlich einfacher von der anderen Seite an diesen Satz heranzugehen, die Skripte der HU Berlin gehen einen ähnlichen weg. Aber fangen wir mal an: ein schönes Beispiel für den Rekursionssatz ist die Selbstreproduktion. Wir wollen also ein Programm, dass bei einer beliebigen Eingabe sich selbst ausgibt. Dazu ist der Rekursionssatz hilfreich.

Formal ausgedrückt:

Zu jeder Funktion $f \in R^{(1)}$ gibt es eine Zahl $n$ mit $\varphi_n = \varphi_{f(n)}$.

Was bedeutet das nun genau und was ist $n$? $n$ ist die Gödelnummer einer Maschine, also quasi unser in natürliche Zahlen codierter Programmcode (kennt Ihr schon, Thema Standardnummerierung). Unsere Programmtransformationsfunktion $f$ bekommt als Eingabe diese Gödelnummer $n$, rechnet darauf rum und gibt uns als Ausgabe eine Gödelnummer $f(n)=k$ aus.

Wenn wir nun die Maschine mit der Gödelnummer $k$ und dem Parameter $x$ starten ($\varphi_k(x)$), so bekommen wie die gleiche Ausgabe, die unser Programm mit der Gödelnummer $n$ und dem Parameter $x$ gehabt hätte ($\varphi_n(x)$), d.h.

$\varphi_n(x) = \varphi_{f(n)}(x)$

Umgangssprachlich gesprochen: Wir können $f$ als eine "Programmumschreibefunktion" betrachten. Nach diesem Satz gibt es Programme, die in ihrer Funktion von unserer Programmtransformationsfunktion $f$ nicht verändert werden. Aber Achtung: nur in der Funktion, d.h. es könnten Programmteile abgeändert oder hinzugefügt werden, die nicht zur Ausführung kommen. Die korrekte und gleiche Funktion/Ausgabe des Programms ist damit dennoch gegeben.

$n$ wird deswegen auch der semantische Fixpunkt der Modifikationsfunktion $f$ genannt.

Damit ist es uns z.B. erlaubt Maschinen zu erstellen, welche eine Beschreibung von sich selbst berechnen und benutzen können. Das ist keineswegs selbstverständlich! Denn lange Zeit galt diese sog. Selbstreproduktion, d.h. Maschinen, die sich selbst nachbauen ohne sich selbst zu enthalten als unmöglich.

Alle Erfindungen, die andere Dinge herstellten wie z.B. eine Autofabrik oder Werkzeughersteller sind komplexer als das erzeugte Produkt und brauchen eine Beschreibung des herzustellenden Produktes. Damit wäre die Selbstreproduktion aber unmöglich, denn um einfache Produkte zu bauen, braucht man komplexe.

Und genau das ist der Trugschluss, den von Neumann 1966 aufgezeigt hat, indem er theoretisch eine einfache Maschine konstruierte, die sich selbst reproduzieren kann:

Diese Maschine besteht aus drei Teilen:

• dem Konstrukteur $K$
  Der Konstrukteur bekommt die Beschreibung einer Maschine (mathematisch gesehen also z.B. unsere Gödelnummer $i$) und setzt diese dann mit den Bauteilen zusammen, so dass wir eine Maschine mit $\varphi_i$ bekommen.
• dem Kopierer $C$
  Der Kopierer kann den Bandinhalt von einem Band auf ein anderes kopieren, so dass am Ende zwei Bänder mit dem selben Inhalt als Ausgabe ausgegeben werden.
• der Steuerung $S$
  Die Steuerung kümmert such um Konstrukteur und Kopierer und versorgt beide mit Eingaben.

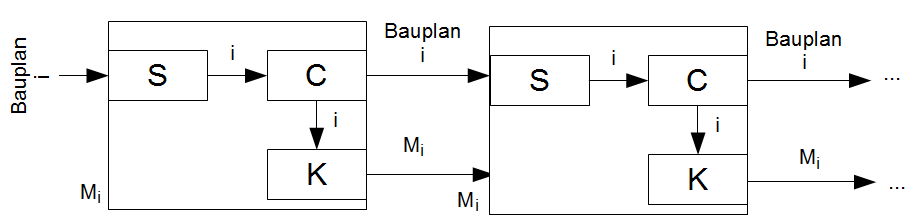
Was wir also brauchen ist, eine Maschine $M$, die bei der Eingabe von sich selbst, sich selbst reproduziert. Und so sieht dann die Maschine aus:

Wir geben den Bauplan $i$ in die Steuerung, diese gibt sie an den Kopierer, welcher den Bauplan verdoppelt. Eine Kopie wird an den Konstrukteur übergeben, der daraus eine neue Maschine $M_i$ baut. Und eben diese neue Maschine (der "Sohn") bekommt dann von seinem "Vater" den Bauplan ausgehändigt und baut dann den "Enkel", eine exakte Kopie von sich selbst usw.

Und nun wieder zurück zur theoretischen Informatik:

Wir haben damit eine Möglichkeit zur Selbstreproduktion und können Maschinen angeben, die sich selbst ausgeben können. Mit dem Rekursionssatz ist es also sichergestellt, dass es ein Programm gibt, welches bei allen möglichen Eingaben sich selbst ausgibt. Eine Anwendung sind z.B. die Quines, denn sie geben bei jeder Ausgabe sich selbst aus, damit gilt der Satz über Selbstreproduktion:

Es gibt eine Zahl $n$, so dass $\varphi_n(x) = n$ für alle $x$.

Wer könnte denn an sowas interessiert sein? Außer Skynet. Viren zu Beispiel.

Just als ich den Beitrag getippt habe, fliegt mir ein Satz Folien um die Ohren, die ich euch nicht vorenthalten will: Folien zur Selbstreproduktion der Uni Potsdam.

Antwort zum Lernziel: Der Rekursionssatz von Kleene besagt, dass man zu einem gegebenen Modifikationsprogramm $f$ immer einen Quelltext finden kann, der trotz Modifikation seine Aufgabe weiterhin erfüllt. Da sich die Semantik des Programms somit nicht ändert wird dieser Quelltext (das $n$) auch semantischer Fixpunkt von $f$ genannt.

Ein Anwendungsbereich dieses Satzes ist die Selbstreproduktion, so dass die Ausgabe von sich selbst der Fixpunkt ist (das Programm gibt sich selbst aus) und es gelten muss: $\varphi_n(x)=n$, egal was man als $x$ eingibt.

Puh, das war ein Haufen arbeit. Wie immer gilt: sollten sich Fehler eingeschlichen haben: bitte wieder Bescheid geben. Danke auch an die Kollegen aus der NG, die so manche einleuchtende Erklärung eingeworfen und zu diesem Text beigetragen haben. Schade, dass die NG jedes Semester gelöscht wird. So verwindet manch eine schöne Erläuterung im digitalen Papierkorb. Vielleicht trägt der Blog ja etwas dazu bei, dass einige Erläuterungen über das Haltbarkeitsdatum der NG bestehen bleiben.

Datum: 4. Dezember 2012
Kategorie: Theoretische Informatik
Kommentarfeed: RSS 2.0 • Trackback: Trackback-Url