Informatik an der Fernuni

Update 2: Fehler korrigiert. Danke Max.

Update 2: Merksatz zum Lernziel hinzugefügt.

Update: aus zwei Beiträgen habe ich mittlerweile drei gemacht. Die Ladezeiten vom smn-Theorem waren ja nicht zu ertragen.

Nun Teil 2 der Kurseinheit 5. Nachdem wir in Teil 1 die Standardnummerierung \(\varphi\) und die Standardkomplexität \(\Phi\) und das \(\Phi\)-Theorem behandelt haben, folgen in diesem und dem nächsten Teil die zwei weiteren Theoreme. Der letzte Beitrag war mit acht Seiten schon relativ lang, hoffentlich wird dieser was kürzer.

Zu früh gefreut, das Beispiel im nächsten Beitrag zum smn-Theorem hat mich ebenfalls 8 Seiten gekostet, daher die Beitragstrennung und der letzte Beitrag der Serie zu KE5 von TIA ist:

• TIA: smn-Theorem (Lernziele KE5, 3/3)

Starten wir zunächst mit einigen Anforderungen an vernünftige Programmiersprachen:

Es gibt zwei Anforderungen an vernünftige Programmiersprachen, die im Skript zu Anfang behandelt wurden. Das sind

• (U) Es soll einen Computer geben, der zu jedem Programm \(P\) und jedem möglichen Eingabewert \(x\) das Resultat \(\sigma(P)(x)\) berechnet und nicht hält wenn \(\sigma(P)(x)\) nicht existiert.
• (S) Zu je zwei Programmen \(P\) und \(Q\) möchte man ein Programm für die Komposition konstruieren können, d.h. es soll eine berechenbare Funktion \(h\) geben, so dass \(\sigma(h(P,Q)=\sigma(Q) \circ\sigma(P)\).

Auch wenn die Programmiersprache RPG wahrscheinlich beide Voraussetzungen erfüllt, vernünftig wird sie dadurch trotzdem nicht. Aber bevor IBM-Fans mir die Fensterscheiben einwerfen machen wir lieber weiter im Text 😉

Lernziel 4

Anwendung und Erläuterung des utm-Theorems

Für die Formalisierung des utm-Theorems brauchen wir zunächst eine hilfreiche Funktion, die wir im letzten Beitrag bereits definiert und als berechenbar bewiesen hatten:

\(h:\mathbb{N}^3 \rightarrow \mathbb{N}\)  mit

\(h(i,n,t) = \begin{cases} 1+\varphi_i(n), & \mbox{ falls } \Phi_i(n) \mbox{ existiert und } \Phi_i(n) \leq t\\ 0, & \mbox{ sonst }\end{cases}\)

Ich werde das jetzt nicht groß ausführen, steht ja alles im ersten Teil der Lernziele zu KE5, sondern sage euch nur schnell noch einmal, was sie macht: Wir bekommen eine \(1+\) das Ergebnis der Maschine mit der Nummer \(i\) bei der Eingabe von \(n\) wenn die Standardkomplexität \(\Phi_i\) existiert und kleiner/gleich \(t\) ist (die Berechnung von \(i\) bei der Eingabe von \(x\) ist noch vor \(t\) Schritten abgeschlossen). Ansonsten gibt es nur eine Null zurück. Fair.

Wie hilft diese Funktion uns nun beim utm-Theorem?

Das utm-Theorem ist definiert als

\(u_\varphi :\subseteq \mathbb{N}^2 \rightarrow \mathbb{N}\) mit

\(u_\varphi(i,x) := \varphi_i(x)\) für alle \(i,x \in \mathbb{N}\).

\(u_\varphi\) ist dann berechenbar und wird die universelle Funktion von \(\varphi\) genannt

Aber wahrscheinlich fügen sich bei euch noch nicht alle Puzzle-Teile zu einem Bild zusammen. Vielleicht holen wir daher zunächst etwas weiter aus: eine universelle Turing-Maschine ist eine Maschine, die beliebige andere Maschinen simulieren kann.

Wie wir im vorherigen Beispiel gesehen haben, können wir einer Turing-Maschine eine andere Maschine und das Eingabewort als Parameter mitgeben und so diese Maschine simulieren. Am Ende kopiert unsere universelle Maschine die Ausgabe auf Band \(0\) und wir sind fertig (nur, dass wir im vorherigen Beitrag noch eine \(1\) zum Ergebnis addiert haben). Die Maschine agiert also als eine Art Interpreter und ist nicht auf die Berechnung einer einzigen Funktion beschränkt.

Was haben wir dazu nun gemacht? Die Turing-Maschinen sprechen nur unär, d.h. Zeichen aus unserem Bandprogramm \(\omega\in BP\) mit \(\omega=(1^2:1,,1)\), mit unseren Klammern, Kommas und Doppelpunkten können wir eigentlich gar nicht interpretieren.

Doch, das können wir! Und zwar mittels der Nummerierung \(\varphi\). Im obigen Beispiel stehen diese zwar im Klartext auf dem Band, aber nur der Übersichtlichkeit halber. Wenn Ihr euch statt einer öffnenden Klammer \((\) nun ihren Nummerierungswert der Ordnungsfunktion \(a\rightarrow\nu_\Omega\) (\(a(„(„)=3\))auf dem Band denkt, dann ist das Jacke wie Hose. Im ersten Teil haben wir gezeigt, dass das durch die Ordnungsfunktion wunderbar funktioniert.

Nachdem wir nun diese Maschine in Zahlen überführt haben, haben wir eine sog. Gödelisierung durchgeführt. Die Codierung, die am Ende für die Maschine herauskommt ist die sogenannte Gödelnummer. Das formale utm-Theorem ist die formale und etwas abstrakte Version dieser universellen Turing Maschine, denn sie erfüllt die am Anfang gestellte Forderung \((U)\) (siehe oben).

Wir können nämlich mit diesem Computer \(U\) (unsere universelle Turing-Maschine) zu jedem Programm \(P\) (welches wir vorher entsprechend codiert haben), das mit einem Eingabewert \(x\) gefüttert werden würde, durch die Simulation/Interpretation von ihm, sein Ergebnis berechnen, also genau unser gesuchtes \(\sigma(P)(x)\).

Das utm-Theorem bedeutet also nichts anderes, als dass eine Funktion \(u_\varphi(i,x)\) (sie nimmt also die Nr. der zu simulierenden Maschine und die Eingabe für sie als Parameter auf) berechenbar ist wenn sie als Ausgabe \(\varphi_i(x)\) (also genau das Ergebnis der simulierten Maschine \(i\)) hat. Genau das bedeutet die obige formale Definition des utm-Theorems.

\(u_\varphi(i,x) := \varphi_i(x)\) für alle \(i,x \in \mathbb{N}\).

Jetzt müssen wir also nur noch eine Maschine angeben, die \(u_\varphi\) berechnet. Unsere Funktion \(h\) von oben leistet uns hier große Dienste: während wir bei \(h(i,n,t)\) im Parameter \(t\) genau angeben mussten, wie lange die simulierende Maschine rechnen darf, wollen wir bei \(u_\varphi\) eig. nur das Ergebnis haben und nicht angeben, wie lange unsere Maschine zu rechnen hat. Das \(t\) ist uns also egal. Und das geht ganz einfach.

Beispiel: wir simulieren das Programm \(h\), welches unser Programm \((1^2:1,,1)(:1,1,1^2)(:B,,)\) mit der Gödelnummer \(n_1\) simuliert, in einer Schleife und zählen unser \(t\) ab \(1\) einfach hoch. Eingabe bleibt \(n = 3\).

1. Führe \(h(n_1,3,1)\) aus und speichere es in \(R_0\)
2. Wenn \(R_0 = 0\) (wir haben die \(HALT\)-Marke im Programm mit unserem \(t=1\) noch nicht erreicht und bekommen daher eine \(0\) als Ausgabe), erhöhe \(t\) um eins und führe dann \(h(2,3,2)\) aus, usw.
3. Wenn \(R_0\) eine Ausgabe ungleich \(0\) hat, dann subtrahiere eine \(1\) vom Ergebnis (in \(h\) haben wir es ja immer um Eins erhöht) und beende dich.

Dam Ende steht in \(R_0\) das Ergebnis (\(3\)) und wir haben unser kleinstes \(t = 8\) auch. Es wird im Skript im Register \(R_3\) zwischengespeichert. Damit ist auch \(u_\varphi\) berechenbar.

Im Skript wird eine weitere universelle Funktion für die Standardkomplexität, nämlich \(u_\Phi\) definiert:

\(u_\Phi :\subseteq \mathbb{N}^2 \rightarrow \mathbb{N}\) mit

\(u_\Phi(i,x) := \Phi_i(x)\) für alle \(i,x \in \mathbb{N}\).

Sie macht nicht viel anders als \(u_\varphi\). Wir bekommen hier jedoch nicht das Ergebnis \(\varphi_i(x)\) als Ausgabe, sondern das kleinste \(t\) (die Anzahl der Rechenschritte, Schrittzahlfunktion, wir erinnern uns?) bei der Eingabe von \(x\), also genau \(\Phi_i(x)\). Das Ergebnis schreiben wir ins \(R_0\), dem Ergebnisregister der berechnenden Maschine und sind fertig.

Zusammenhang zu \(R^{(1)}\)

Nachdem ich gemerkt habe, dass ich einige Details von \(P^{(1)}\) und \(R^{(1)}\) durcheinander brachte und freundlich von Harald und Carsten aus der NG darauf hingewiesen wurde, habe ich mich entschlossen das hier auch nieder zu schreiben. Obwohl ich der Meinung bin, dass die meisten von euch die Unterschiede zwischen den beiden Mengen gut bewusst sind und sie keine Auffrischung brauchen, bin ich mir sicher, dass ich das in spätestens einigen Monaten vor der Prüfungsvorbereitung wieder verdrängt habe. Also tue ich etwas für mein „Zukunfts-ich“ (How i met your mother lässt grüßen) und schreibe in aller Deutlichkeit nochmal:

\(P^{(1)}\): partielle (nicht überall definierte), berechenbare Funktionen. Nummerierung \(\varphi\) von \(P^{(1)}\) erfüllt das utm-Theorem, d.h. es gibt eine universelle Turingmaschine, die die Funktion interpretiert und die entsprechende Ausgabe berechnet.

\(R^{(1)}\): totale (überall definierte), berechenbare Funktionen. Keine Nummerierung von \(R^{(1)}\) erfüllt das utm-Theorem (es gibt also keine universelle Funktion \(u\) zum interpretieren des Programms).

Die letzte Feststellung ist wichtig: warum erfüllt keine Nummerierung von \(R^{(1)}\) das utm-Theorem? Denn es wäre doch – wie im Skript angemerkt – praktisch wenn man sich nur auf überall definierte Funktionen beschränken könnte. Was nützt einem ein Programm, dass bei einer Eingabe ggf. nicht hält? Leider geht das nicht. Die Beweisidee ist wie folgt:

Zunächst: was ist eine Nummerierung? Einfach nur die Nummer einer Funktion. Während wir also \(P^{(1)}\), die einstelligen, berechenbaren, ggf. partiellen Funktionen mit \(\varphi\) nummeriert haben und diese Funktion (bzw. die Maschinen, die die Funktionen berechnen) durch eine universelle Turingmaschine mit \(u_\varphi(i,x)=\varphi_i(x)\) simulieren, können, bekommen wir bei \(R^{(1)}\) ein Problem.

Warum? Während \(\varphi_i(x)\) nicht für jedex \(x\) definiert sein muss, d.h. es auch eine Ausgabe \(\varphi_i(x)=div\) geben kann, haben wir bei dem gleichen Spiel mit \(\psi\), der Nummerierung von \(R^{(1)}\) immer eine Ausgabe. Ist ja auch klar, die Funktionen aus \(R^{(1)}\) sind total und damit eben für jedes \(x\) definiert.

In was für ein Problem laufen wir hier?

Wir nehmen eine Nummerierung \(\psi\) von  \(R^{(1)}\). Lt. utm-Theorem gibt es dazu eine universelle Funktion \(u_\psi(i,x)=\psi_i(x)\), d.h. eine universelle Turing-Maschine, welche als Eingabe die Gödelnummer/den Index der Maschine und ein \(x\) bekommt und diese so simuliert (siehe das 2. Beispiel für \(h\) von oben), dass auf Band \(0\) anschließend die Ausgabe \(\psi_i(x)\) steht.

Nun basteln wir uns eine Funktion \(h(i)=u_\psi(i,i)+1\). Diese ist auch total und berechenbar, da \(\psi(i,i)\) ja selbst total und berechenbar war. D.h. die universelle Funktion \(u\) simuliert uns die Maschine \(i\) mit der Eingabe \(i\) und addiert eine \(1\) dazu. Sie ist damit definitiv von \(\psi(i,i)\) verschieden und somit eine neue Maschine.

Da es eine komplett neue Maschine ist, hat sie natürlich auch eine neue Gödelnummer/einen neuen Index \(k\). Da wir aber alle totalen Funktionen bereits durchnummeriert haben, ist \(h(k) = \psi_k(k) = \psi_k(k)+1\), was aber nicht funktioniert. Denn \(\psi_k(k)\) existiert ja bereits in unserer Auflistung und kann ja gar nicht eine neue Maschine sein.

Das ist wieder ein Beweis durch Diagonalisierung: wir sind von der Vollständigkeit unserer Auflistung ausgegangen und haben offensichtlich trotzdem noch eine neue Maschine erstellen können, was uns zu einem Widerspruch führt. Damit erfüllt keine Nummerierung nur der totalen, berechenbaren Funktionen \(R^{(1)}\) das utm-Theorem.

Und was ist mit \(P^{(1)}\)? Damit klappt es:

Wir gehen zunächst genauso vor, wie bei \(R^{(1)}\): holen uns eine Nummerierung mit \(\varphi\) und eine universelle Funktion \(u_\varphi(i,x)=\varphi_i(x)\).

Nun erstellen wir die neue Funktion: \(h(i)=u_\varphi(i,i)+1\). Da \(\varphi(i,i)\) nicht total sein muss (für ein \(x\) kann \(\varphi(i,x)=div\) sein), könnte \(h(i)=u_\varphi(i,i)+1\) ebenfalls nicht total sein und die Aussage \(h(k)=\varphi_k(k)=\varphi_k(k)+1\) hätte durchaus Bestand: \(h(k)=\varphi_k(k)=div=\varphi_k(k)+1=div+1=div\).

Ist tatsächlich etwas abstrakt, aber hoffentlich trotzdem nachvollziehbar.

(Hier geht ein großer Dank an Barbara, Harald, Oliver und Herbert aus der NG für ein paar – wenn auch hinkende – Vergleiche 😉 Wenn jemand in „einfacheren Worten“ eine Erklärung hat, warum eine Nummerierung für \(P^{(1)}\) das utm- Theorem erfüllen kann, aber keine Nummerierung für \(R^{(1)}\) das zu leisten vermag, der möge mir bitte eine Nachricht schicken. Ich würde das dann gerne hier aufnehmen)

Antwort zum Lernziel: bei dem utm-Theorem geht es im Grunde um die Frage ob es einen Computer gibt, der jeden anderen Computer simulieren kann. In der theoretischen Informatik wäre es zwar unproblematisch für jede Aufgabe eine eigene Maschine anzugeben, ist aus praktischer sicherlich kein gangbarer Weg.

Diese Fragestellung hat große Bedeutung bei den Programmiersprachen, denn nur durch die Bejahung dieser Frage können Programmiersprachen durch Computer interpretiert und so Anwendungen auf ihnen ausgeführt werden.

Daher betrachten wir den Computer als universelles Gerät, dass Programme (andere Computer sozusagen, die nur eine Funktion berechnen) und Daten entgegen nimmt und die Funktion des Programms auf den entgegen genommenen Daten simuliert.

Frage ist hierbei: gibt es denn so eine Funktion, die auf einer Turingmaschine ausgeführt, eine andere Funktion simulieren kann? Und genau diese Funktion wird universelle Funktion \(u\) genannt, die als Eingabe eine Gödelnummer \(i\) des zu simulierenden Programms \(\omega\) und die Eingabedaten \(x\) entgegen nimmt und auf diesen die Befehle des Programms Schritt für Schritt durchführt um am Ende die gleiche Ausgabe zu haben wie das Programm selbst: \(u_\varphi(i,x)=\varphi_i(x)\).

In unserem Beweis im letzten Betrag hat es unsere Funktion \(h\) für uns erledigt (wobei sie noch die maximale Anzahl der zu rechnenden Schritte verwendet hatte).

Merksatz:

Das formale utm-Theorem ist die formale und etwas abstrakte Version dieser universellen Turing Maschine. Es besagt, dass eine universelle Funktion existiert, die jede andere berechenbare Funktion berechnen kann.

Im nächsten Beitrag geht es dann um das smn-Theorem und Rekursionssätze.

Update: Tippfehler, Danke Marcel.

Update: Ungenauigkeit beseitigt. Danke Steve.

Update: Fehler beseitigt. Danke Max.

Update: Pfui, da sind mir doch tatsächlich ein paar Funktionen abhanden gekommen. Sind alle wieder im Text. Auch habe ich einen weiteren Betrag verfasst um den Zusammenhang zwischen einer Programmiersprache und \(\varphi\) sowie dem utm- und smn-Theorem noch etwas zu verdeutlichen.

Update: Fehler beseitigt.

Update: ein paar Details zur Standardnummerierung \(P^{(1)}\) habe ich noch hinzugefügt. Denn die ist nicht bijektiv, sondern nur surjektiv. Das wollte ich unbedingt noch einmal hervorheben, da es im letzten Beitrag so ausgesehen hat, als wären alle Standardnummerierungen bijektiv, was für \(P^{(1)}\) nicht stimmt.

Update: beim erneuten Lesen sind mir einige Fehler aufgefallen, die ich nun (hoffentlich) ausgemerzt habe. Auch habe ich die Lernziele etwas umgestellt, so dass sie zwischen den zwei Beiträgen besser passen. Wenn also noch irgendwo Verweise sein sollten, wo sie nicht hingehören: bitte Bescheid geben.

Die Antworten zu den Lernzielen habe ich noch nicht ausformuliert, kommt aber gleich noch.

Weil’s so schön war: nochmal entlang der Lernziele, diesmal aus KE5. Die Lernziele zu KE5 bestehen aus zwei drei Beiträgen: diesem hier, dem zweiten und dritten Teil mit:

• TIA: utm-Theorem (Lernziele KE5, 2/3)
• TIA: smn-Theorem (Lernziele KE5, 3/3)

Wir starten im ersten Teil direkt mit dem ersten Lernziel: der Standardnummerierung für \(P^{(1)}\)

Lernziel 1

Erläuterung der Definition der Standardnummerierung \(\varphi\) von \(P^{(1)}\)

Was eine Standardnummerierung ist, wissen wir bereits aus dem Beitrag zu KE4. Sie ist (im Kontext von KE4) eine bijektive Abbildung zwischen den natürlichen Zahlen \(\mathbb{N}\) und einer anderen Menge. Im letzten Beitrag haben wir alle Worte über dem Alphabet \(\Sigma\), nämlich \(\Sigma^{*}\) standard-nummeriert. In diesem Beitrag kümmern wir uns um die einstelligen, berechenbaren Zahlenfunktionen \(P^{(1)}\).

Nur hier gibt es ein kleines Problemchen:

Ihr wisst doch noch, was dort der Unterschied zwischen einer Nummerierung und einer Standardnummerierung ist? Nein? Schämt euch! Wurde alles im letzten Beitrag durchgekauft. Aber trotzdem:

• Eine Nummerierung muss nicht bijektiv sein, Surjektivität reicht.
• Eine Standardnummerierung jedoch ist eine bijektive Abbildung zwischen zwei Mengen.

Durch eine bijektive Abbildung zwischen zwei Mengen zeigen wir unter anderem, dass diese gleichmächtig sind. Wo liegt nun das Problem? Kommt gleich, versprochen! Behaltet einfach erst einmal im Hinterkopf, dass die Bijektion für eine Standardnummerierung unserer \(P^{(1)}\) keinen Bestand hat.

Im Skript ist \(BM\) die Menge der normierten Bandmaschinen mit dem Alphabet \(\{1,B\}\). Im Gegensatz zu den Bandmaschinen mit beliebigen Hilfsalphabeten sind diese jedoch nummerierbar.

Zunächst sollte man sich nochmal ins Gedächtnis rufen, dass wir jede (Register-berechenbaren) Zahlenfunktion mittels Standardnummerierung in (Turing-berechenbare) Wortfunktionen und umgekehrt überführen können. Was hier am Ende passieren soll ist, dass wir von einer natürlichen Zahl über die Funktion \(\nu_P\) zu einem Bandprogramm kommen. Von diesem ausgehend kommen wir mit \(\nu_M\) auf eine normierte Bandmaschine (bzw. das Flussdiagramm aus diesem). Anschließend können wir diese mit \(\xi\) in eine einstellige, berechenbare Funktion aus \(P^{(1)}\) abbilden und haben zum Schluss über mehrere Wege also eine Nummerierung der einstelligen, berechenbaren Funktion \(P^{(1)}\) erreicht. Aber mal langsam.

Die Nummerierung \(\varphi\) besteht im Skript aus vier Komponenten:

• Ordnungsfunktion \(a\) für das Alphabet \(\Omega\), so dass wir mit \(\nu_\Omega\) die Standardnummerierung aller Worte aus \(\Omega\), d.h. von \(\omega\in\Omega^{*}\) haben. Also nicht nur Programme, sondern auch Kauderwelsch wie z.B. \(„1B(:“\).
• \(\nu_P : \mathbb{N} \rightarrow BP\), z.B. \(\nu_P(i)\) als die Nummerierung des Bandprogramms \(i\). Es ist definiert durch:
• \(\nu_P(i)=\begin{cases}\nu_\Omega(i)&\text{ wenn }\nu_\Omega(i)\in{BP}\\“(:B,,)“&\text {sonst}\end{cases}\)

  Wir bekommen damit zur Nummer \(i\) das zugehörige Bandprogramm wenn es tatsächlich ein Bandprogramm ist. Oder einfach nur eine Endlosschleife wenn die Nummer \(i\) zu irgendwelchem Kauderwelsch gehört, denn mit \(\nu_\Omega\) haben wir (siehe oben) alle Worte über \(\Omega\), d.h. auch Unsinn, nummeriert.

• \(\nu_M : \subseteq \Omega^* \rightarrow BM\), damit bekommen wir zum Wort \(\omega\) aus \(\Omega^{*}\) die zugehörige Bandmaschine \(M\) (dazu gleich mehr)
• Funktion \(\xi:BM \rightarrow P^{(1)}\) mit  \(\xi(M) := \iota^{-1}{f{_M}}\iota\). \(\xi(M)\) ist also die Funktion aus \(P^{(1)}\), welche die Funktion der Bandmaschine \(M\) berechnet.

Damit kann die Standardnummerierung \(\varphi\) als eine Komposition zwischen \(\xi\circ\nu_M\circ\nu_P\) definiert werden.

Das Problem ist nun, dass diese Standardnummerierung \(\varphi\) nicht bijektiv ist, wie die Standardnummerierung \(\nu_\Sigma\)! Das liegt an der Surjektivität der verwendeten Funktionen, u.a. \(\xi :BM \rightarrow P^{(1)}\). Denn zu einer Funktion aus \(P^{(1)}\) kann es durchaus mehrere Bandmaschinen aus \(BM\) geben, die die Funktion berechnen: wir fügen der Berechnungsroutine einfach ein paar sinnlose Schleifen hinzu und haben so eine neue Maschine, aber immer noch die alte, berechnete Funktion.

Jedoch ist sie trotzdem total, denn die Nummerierung aller Bandprogramme \(\nu_P : \mathbb{N} \rightarrow BP\) ist ja total: wir erwischen durch die Definition von \(\nu_P\) tatsächlich nur richtige Bandprogramme. Und zwar alle.

Und zu einem Bandprogramm bekommen wir die zugehörige Bandmaschine mit \(\nu_M\). Der Definitionsberech der Funktion \(\nu_M\) ist durch die Totalität von \(\nu_P\) die komplette Menge \(BP\).

Die Komposition aus \(\nu_M(\nu_P)\) ist damit auch total. Und weil \(\xi : BM\rightarrow{P^{(1)}}\) auch total ist (wir haben zu allen Funktionen aus \(P^{(1)}\) min. eine Bandmaschine, die sie berechnet), ist die Komposition \(\xi\circ\nu_M\circ\nu_P=\xi(\nu_M(\nu_P))\) ebenfalls total.

Um es etwas deutlicher zu machen, holen wir uns Beispiele und bauen auf diesen dann die Definition auf:

Zunächst haben wir ein Alphabet \(\Omega\), welches unsere Zeichen

\(\Omega:=(1\mid{B}\mid{(}\mid{)}\mid{,}\mid{:}\mid{R}\mid{L})\)

beinhaltet. Achtung \(\mid\) ist unser Trennzeichen, da das Komma zum Alphabet \(\Omega\) gehört.

Aus diesen Zeichen kann ein Bandbefehl \(BB\) unseres Programms bestehen, welches die Form

\((1^m:\beta,1^n)\) mit \(\beta\in\{B,1,R,L\}\) oder

\((1^m:\beta,1^k,1^n)\) mit \(\beta\in\{B,1\}\)

hat. Das kennt Ihr alles schon von den Turingmaschinen. Der erste Befehl der Marke \(1^m\) schreibt entweder ein \(B\), eine \(1\) auf das Band oder geht nach \(L\)inks oder \(R\)echts und springt anschließend in die Marke \(1^n\).

Der zweite Befehl ist eine Verzweigung: in der Marke \(1^m\) wird geprüft ob unter dem Lesekopf aktuell ein \(B\) oder eine \(1\) steht. Ist das der Fall, wird in die Marke \(1^k\) verzweigt und ansonsten in die Marke \(1^n\) gesprungen.

An den Beispiel weiter unten wird es gleich deutlicher.

Ein Bandbefehl aus der Menge \(BB\) ist damit ein Wort über \(\Omega\), d.h. \(BB\subseteq\Omega^{*}\). Ein Bandprogramm aus der Menge \(BP\) ist eine Folge von Bandbefehlen (es kann auch nur eines seit) und ist damit auch nur eine Kombination aus Worten über \(\Omega\): \(BP\subseteq\Omega^{*}\)

Kommen wir nun zu unserer Funktion, die uns zu einem Bandprogramm aus \(BP\) eine Bandmaschine aus \(BM\) gibt, die die gleiche Funktion berechnet:

\(\nu_M:BP\rightarrow BM\)

Die Maschine \(M\in{BM}\), die das Bandprogramm \(\omega\in{BP}\), welches aus einer Folge von Bandbefehlen aus der Menge \(BB\) besteht, berechnet, wird durch ein Flussdiagramm \(F\) beschrieben. Damit gilt:

\(M=\nu_M(\omega)\in{BM}\)

D.h. mit der Funktion \(\nu_M(\omega)\) bekommen wir zum Bandprogramm \(\omega\) die passende Maschine \(M\)

Wir haben noch die Definition von \(F\) im Kopf? Nein? Macht nichts: \(F := \{Q,D_{\{1,B\}},\sigma, q_0\}\).

\(Q\): ist die Menge unserer Marken, d.h. die Beschriftung der Befehle und Verzweigungen (Rechtecke und Rauten) im Flussdiagramm.

\(D\): ist unser Arbeitsalphabet. Wir beschränken uns im Skript auf \(\{1,B\}\), da sie die einzigen Zeichen sind, die wir benötigen (Satz über Hilfssymbole!)

\(\sigma\): die auszuführenden Aktionen für die Marken. Ist z.B. \(n\) eine Marke, so ist \(\sigma(n)\) der auszuführende Befehl.

\(q_0\): unsere Startmarke. Diese ist der Definition nach das erste Element aus \(\omega\), d.h. der erste Befehl.

Wir überführen also die Folge von Bandbefehlen im Endeffekt einfach in ein Flussdiagramm. Das geschieht nachfolgendem Schema:

Für \((1^n:\beta,1^k)\) bekommen wir

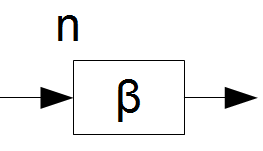
und für \((1^n:\beta,1^m,1^k)\) gibt es ein

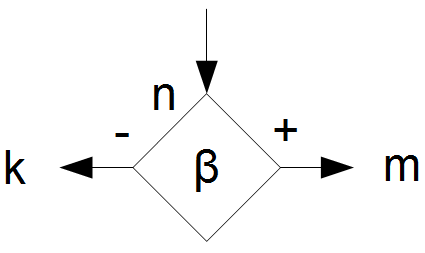
Was mich zunächst aus dem Konzept gebracht hat, sind Befehle und Übertragung dieser in ein Flussdiagramm in folgender Form: \((:1,1,1^2)\), doppelte Zuweisungen zu einer Marke und \(HALT\)-Befehle. Die folgenden Sätze liefern hierzu den Schlüssel (Harald aus der NG hat mich hier drauf gestoßen. Danke nochmal):

1. Falls es für eine Zahl/Marke \(k\) mehrere Befehle gibt, so zählt nur der erste von links.

2. Kommt irgendwo eine Zahl/Marke \(k\) vor und beginnt kein Befehl mit \(1^k\), so ist es der HALT-Befehl.

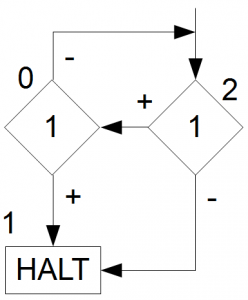
Beispiel: aus dem Skript \(\omega = (1^2:1,,1)(:1,1,1^2)(:B,,)\)

Was müssen wir hier also zunächst tun? Wir schreiben uns alle Marken raus, die wir finden: 2 (aus \((1^2:…)\)), 0 (aus \((:…)\)) und 1 (aus \((…,1)\)). Nun schauen wir uns die Definitionen unserer Marken 0,1 und 2 an.

• Marke 0: \((:1,1,1^2)\). Bedeutet: wenn \(1\), gehe zu Marke \(1\), ansonsten zu Marke \(2\). \((:B,,)\) wird ignoriert, da doppelte Zuweisung.
• Marke 1: \(HALT\). Es wird auf die Marke \(1\) in Marke \(0\) und \(2\) verwiesen, aber es gibt keinen Befehl dafür. Also ist es unsere \(HALT\)-Marke.
• Marke 2: \((1^2:1,,1)\). Bedeutet: wenn \(1\), gehe zu Marke \(0\), ansonsten zu Marke \(1\). Ist unsere erste Marke und daher auch unser Einstiegspunkt im Flussdiagramm.

Mit diesen Informationen könnt Ihr euch nun das dazugehörige Flussdiagramm eurer Maschine \(M\) aufmalen (versucht es mal selbst und prüft eure Lösung mit dem Spoiler-Ausklapp-Text unten) und habt damit euer \(\nu_M(\omega)\).

Lösung zeigen

Und nun tun wir das wozu wir hier sind: wir definieren wir die Standardnummerierung \(\varphi\) dem Skript nach.

1. Ordnungsfunktion \(a\), welche die Zeichen (siehe oben) unserer Programmiersprache nummeriert. \(a_1 = 1\), \(a_2 = B, … a_8 = L\), usw. Mit \(\nu_\Omega\) wird dann die Standardnummerierung von \(\Omega^*\) bezeichnet, denn \(\Omega^*\) beinhaltet (wir denken wieder an den Beitrag über die Standardnummerierung) ja alle Worte über diesem Alphabet.D.h. wir können diese Kombinationen aus diesen Zeichen durchnummerieren.
2. Mit \(\nu_P : \mathbb{N} \rightarrow BP\) haben wir eine Funktion, die uns zu einer Zahl \(i\) das zugehörige Bandprogramm aus \(BP\) (bzw. eine Kombination aus den oben definierten Zeichen) zurückgibt: nämlich \(\nu_\Omega (i)\) (aber nur wenn es ein echtes Bandprogramm ist, welche wiederum aus Bandbefehlen der Menge \(BB\) besteht. Es könnte aber auch irgendwelches Kauderwelsch sein, was nicht ausführbar ist).

   Wenn es also Kauderwelsch ist, wird ein \(((:B,,)\). zurückgegeben, d.h. eine Endlosschleife. Damit ist \(\nu_P\) nur surjektiv, da man einige Nummern \(i\) mit \(\nu_P(i)\) durchaus mehrfach auf \(((:B,,)\) abbildet wenn sie nicht Nummern von legitimen Bandprogrammen sind.

3. \(\nu_M : \subseteq \Omega^* \rightarrow BM\), damit bekommen wir zum Wort \(\omega\) aus \(\Omega^{*}\) (von wem wir durch \(\nu_P\) sicher wissen, dass es sich um ein Bandprogramm handelt), die zugehörige Bandmaschine \(M\)
4. Durch \(\xi:BM\rightarrow P^{(1)}\) mit  \(\xi(M):=\iota^{-1}{f{_M}}\iota\) haben wir die von der Bandmaschine \(M\) berechnete Funktion aus \(P^{(1)}\). Zudem: \(\iota(i) = 1^i\). Bei den beispiel gleich wird es deutlicher.
5. Als letztes definieren wir \(\varphi:\mathbb{N}\rightarrow P^{(1)}\) durch: \(\varphi_i=\varphi(i)=\xi\nu_M\nu_P (i)\). Auch hier hilft zum besseren Verständnis das Ausklammern: \(\varphi_i=\varphi(i) = \xi(\nu_M (\nu_P (i)))\).

Punkt 4 baut auf der ganzen Vorarbeit auf und standard-nummeriert uns schlussendlich unsere einstelligen, berechenbaren Funktionen aus \(P^{(1)}\). Und nicht vergessen: die Standardnummerierung von \(P^{(1)}\) ist surjektiv und total!

Ein Beispiel wäre hilfreich, oder? Ich nehme gleich das Beispiel aus dem Skript und rechne es Schritt für Schritt durch.

Beispiel: \(\omega_1 = (: R,1)(1:B,11,)\)

Die Nummer des Bandprogramms ist in der Aufgabenstellung \(n_1\). Das ist relativ willkürlich gewählt uns ist uns auch ziemlich egal. Wir könnten durch die ordnungsfunktion \(a\) auch eine echte Gödelnummer angeben, aber wozu? Spielt hier keine große Rolle.

Wir haken nun die komplette Definition der Standardnummerierung ab:

1. Als Ordnungsfunktion \(a\) nutzen wir die Funktion aus der Definition und haben so auch unsere Nummerierung von allen Worten über dem Alphabet \(\Omega\), nämlich \(\nu_\Omega\).

2. Nun brauchen wir \(\nu_P(n_1)\). Da unser Wort \(\omega_1 = (: R,1)(1:B,11,)\) korrekt ist und aus \(BP\) kommt, bekommen wir das zurück (siehe Definition):

\(\nu_P(n_1)=\nu_\Omega(n_1)=\omega_1=(: R,1)(1:B,11,)\).

Wäre \((: R,1)(1:B,11,)\) nicht in \(BP\), so hätten wir nur ein \((:B,,)\) bekommen. Daraus basteln wir uns nun ein wunderschönes Flussdiagramm. Auch hier: alleine versuchen, dann Lösung öffnen.

Lösung zeigen

Was macht das schöne Stück? Nehmen wir an wir geben in die Maschine \(11\) und starten bei Marke \(0\). Der Lesekopf ist anfangs ja auf dem letzten \(B\) (Blank) vor dem Eingabewort. Wir gehen nun nach rechts (Marke \(0\)) auf die erste \(1\) auf dem Band. Dann sind wir bei Marke \(2\) und prüfen ob unter dem Lesekopf ein \(B\) (Blank) steht. Tut er das, gehen wir zu Marke \(2\) und halten. Befindet sich jedoch eine \(1\) unter dem Lesekopf, gehen wir wieder zu Marke \(0\) und tun das so lange bis wir auf ein Blank treffen und unser Eingabewort damit zu Ende ist.

Soweit so unspektakulär.

Die so berechnete Funktion \(f\) unserer Maschine \(M\) ist somit: \(f_{M}(1^m) = 1^m\). Zur Auffrischung. Das \(m\) ist einfach nur die Anzahl der Einsen. Wir geben also \(m\) Einsen auf das Band und am Ende steht der Lesekopf auf Position \(m+1\) und wir haben als Ausgabe links vom Lesekopf also \(m\) Einsen auf dem Band. Sprechen wir von „normalen“ Funktionen, die dezimal (\(x\)) und nicht unär (\(1^{x}\)) definiert sind, wäre das \(f(x) = x\).

Nun brauchen wir noch unser \(\varphi\) (ich erkläre die Berechnung weiter unten um die Übersichtlichkeit nicht zu killen):

\(\begin{array}{lcl}\varphi_{n_1}(m)&=& \varphi(n_1)(m)& {*1} \\ {} &=& \xi(\nu_M(\nu_P(n_1)))(m) & {*2} \\ {} &=& \xi(\nu_M((: R,1)(1:B,11,)))(m) &\mbox{*3}\\{} &=& \xi(M)(m)&\mbox{*4}\\{}&=&\iota^{-1}(f_M(\iota(m)))&\mbox{*5}\\{}&=&\iota^{-1}(f_M(1^m))&\mbox{*6}\\{}&=&\iota^{-1}(1^m)&\mbox{*7}\\{}&=&m&\mbox{*8}\end{array}\)

Fertig!

Wir haben es also geschafft mit \(\varphi\) die Funktionen aus \(P1 {(1)}\) zu nummerieren. Geben wir \(\varphi\) also die dezimale Nummer der Maschine und einen dezimalen Parameter aus \(\mathbb{N}\) mit, bekommen wir als Ausgabe auch einen dezimalen Ausgabewert zurück, obwohl die Maschine, die diesen Wert berechnet nur mit der unären Darstellung \(1^m\) arbeitet. Wir verkürzen das in den Merksatz:

\(\varphi(i)\) ist die von der \(i-ten\) Bandmaschine berechnete Funktion aus \(P^{(1)}\), der Menge der einstelligen partiell-rekursiven Funktionen.

Hier die Erklärung der Berechnung von oben (Danke an Carsten für den letzten Hinweis).

\(*1\): nur schöner umgeschrieben, einfach der Definition nach

\(*2\): der Definition nach ist \(\varphi(i)=\xi\nu_M\nu_P(i)\). Ich habe hier nur ausgeklammert. Und da wir \(\varphi(i)\) mit einem Parameter \(m\) füttern, hängt er eben mit hinten dran.

\(*3\): \(n_1\) war ja die willkürliche Nummer unserer Maschine. \(\nu_P(n_1)\) ist demnach unser Wort \(\omega_1 = (: R,1)(1:B,11,)\) für die Maschine (siehe Definition von \(\nu_P\)).

\(*4\): \(\nu_M((: R,1)(1:B,11,))\) ist also unsere Maschine \(M\) mit dem Flussdiagramm, welche unsere Funktion berechnet. Die von der Maschine \(M\) berechnete Funktion nennen wir ja immer \(f_M\).

\(*5\): \(\xi(M)\) ist unserer Definition nach ja eben \(\iota^{-1}(f_M(\iota))\). Da wir ja immernoch den Parameter \(m\) mitschleppen, hängt er weiterhin einfach nur mit.

\(*6\): Jetzt wird es lustig. In der Definition steht, dass \(\iota(m) = 1^m\) ist. D.h. einfach die Anzahl von Einsen. \(\iota(4)\) wäre z.B. \({} = 1^4 = 1111\). Das dient uns als Eingabe für unsere Funktion \(f_M\). Die Bandmaschinen werden ja mit der unären Darstellung von Dezimalzahlen gefüttert. Daher brauchen wir hierfür \(\iota\) um eine Dezimalzahl in ihre unäre Darstellung umzuwandeln damit wir unsere Maschine damit bedienen können.

\(*7\): Was macht unsere Funktion \(f_M\) wenn man sie mit der Eingabe \(1^m\) startet? Genau: sie gibt uns als Ausgabe auch wieder \(1^m\) zurück.

\(*8\): Und \(\iota^{-1}\) ist die Inverse zu \(\iota\) und macht genau das umgekehrte. Es bekommt als Parameter die unäre Darstellung \(1^m\) der Zahl \(m\) als Parameter und gibt uns die dezimale Darstellung \(m\) zurück.

Damit haben wir auch die Standardnummerierung \(\varphi\) der einstelligen, berechenbaren Funktionen \(P^{(1)}\) abgehakt.

Ich gehe in diesem Abschnitt jetzt nicht strikt den Lernzielen, da zu dieser Aufgabe auch noch die Standardkomplexität \(\Phi\) gehört. Im anderen Beitrag wäre sie nicht wirklich gut aufgehoben. Aus diesem Grund nehme ich das noch hier auf. Aber zunächst die Antwort zum Lernziel.

Antwort zum Lernziel: Die Standardnummerierung \(\varphi\) der einstelligen, berechenbaren Funktionen \(P^{(1)}\) besteht aus den Komponenten:

• Ordnungsfunktion \(a\) mit \(a:\{1,…,8\}\subseteq\Omega\) für die geordnete Nummerierung des Alphabets \(\Omega\)
• \(\nu_\Omega\). Durch die Ordnungsfunktion induzierte Standardnummerierung von von \(\Omega^{*}\).
• \(\nu_P(i):\mathbb{N}\rightarrow BP\). Funktion um zu einer Nummer \(i\) das zugehörige Bandprogramm zu bekommen wenn \(\nu_\Omega(i)\) tatsächlich ein Bandprogramm ist
• \(\nu_M(i):BP\rightarrow BM\). Funktion um zur einem Bandprogramm die zugehörige Bandmaschine zu bekommen.
• \(\xi:BM\rightarrow P^{(1)}\). Funktion um zu einer Maschine die zugehörige Funktion zu erhalten.

Dadurch ist es möglich, ausgehend von einer Zahl \(i\in\mathbb{N}\) eine Funktion aus \(\varphi(i)\in{P^{(1)}}\) zu erhalten:

\(\varphi: \mathbb{N}\rightarrow BP\rightarrow BM\rightarrow P^{(1)}\)

Lernziel 2

Erläuterung des \(\Phi\)-Theorems

Wir starten zunächst mit der Definition der Standardkomplexität selbst:

\(\Phi\) heißt Standardkomplexität zu \(\varphi\) und ist definiert durch:

\(\Phi(i)(x):=\Phi_i(x) := SZ_i(q_{0i}, (\varepsilon, B, 1^x))\)

\(q_{oi}\) ist die Anfangsmarke, \(SZ_i\) die Schrittzahlfunktion der Bandmaschine \(\nu_M(\nu_P(i))\).

Was haben wir hier?

Im Endeffekt bekommen wir mit \(\Phi\) also einfach nur die Anzahl der Schritte, die die Maschine \(\nu_M(\nu_P(i))\) braucht um für eine Eingabe \(x\), ausgehend von Marke \(q_{oi}\) und der Bandbelegung \((\varepsilon, B, 1^x)\) (unter dem Lesekopf steht das Blank \(B\) vor der Eingabe, einer unären Darstellung von \(x\)) die Berechnung durchzuführen und schließlich auf \(HALT\) stehen zu bleiben (oder eben nicht). Dafür brauchen wir die Schrittzahlfunktion \(SZ\), die wir bereits kennen.

\(\nu_M(\nu_P(i))\) schreckt euch doch nach dem Abschnitt zur Standardnummerierung \(\varphi\) von \(P^{(1)}\) doch auch nicht mehr, so dass ich es nicht an einem Beispiel auflösen muss, oder? Nein? Gut. Dann machen wir weiter.

Die Standardkomplexität \(\Phi\) zu \(\varphi\) hat zudem drei schöne Eigenschaften:

1. Die Funktion zur Standardkomplexität \(\Phi\) einer Maschine \(i\) gehört zu den einstelligen, berechenbaren Funktionen \(P^{(1)}\).

Ist auch klar, denn es ist die Rechenzeitfunktion der \(i\)-ten Bandmaschine.

2. Der Definitionsbereich von \(\Phi_i\) ist gleich dem Definitionsbereich von \(\varphi_i\). Beide Funktionen verwenden den selben Parameter \(x\) aus \(\mathbb{N}\) für ihre Eingabe.

Während \(\varphi_i(x)\) uns das Ergebnis \(y\) aus seinem Bildbereich liefert, bekommen wir mit \(\Phi_i(x)\) die zur Berechnung von \(y\) notwendige Schrittanzahl \(z\).

Dass \(y \neq z\) sein kann (mit etwas Zufall ist die Anzahl der Schritte gleich dem Ergebnis, aber das ist dann auch nur Zufall), für das gleiche \(x\), ist auch klar. Aber es bleibt das gleiche \(x\), daher ist

\(Def(\Phi_i) = Def(\varphi_i)\).

3. Die Menge \(\{(i,x,t) \in \mathbb{N}^3\mid \Phi_i(x) \leq t\}\) ist rekursiv/entscheidbar.

Während Punkt Eins und Zwei wahrscheinlich klar sind, wiederholen wir für Punkt 3 noch einmal die Definition einer rekursiven/entscheidbaren Menge aus einem alten Beitrag. Wann ist eine Menge also rekursiv/entscheidbar? Genau dann wenn die charakteristische Funktion berechenbar ist. Die charakteristische Funktion für \(\Phi\) ist:

\(g_\Phi(i,x,t)=\begin{cases} 1, & \mbox{ falls } \Phi_i(x) \leq t \\ 0, & \mbox{ sonst}\end{cases}\)

Was bedeutet das?

Ganz einfach: wir bekommen mit der Funktion \(g_\Phi(i,x,t)\) eine \(1\) zurück wenn die Maschine \(\nu_M(\nu_P(i))\) bei der Eingabe von \(x\) nicht mehr als \(t\) Rechenschritte bis zur \(HALT\)-Marke braucht. Braucht sie mehr, so bekommen wir eine \(0\) zurück.

Als Beweis benutzen wir wieder eine Funktion, die unserem \(h(i,n,t)\) (Erläuterung von \(h\) ist im nächsten Lernziel) sehr ähnlich ist.

\(h(i,n,t) = \begin{cases} 1+\varphi_i(n), & \mbox{ falls } \Phi_i(n) \mbox{ existiert und } \Phi_i(n) \leq t\\ 0, & \mbox{ sonst }\end{cases}\)

Der Beweis, dass diese Funktion berechenbar ist, gehört auch zu den Lernzielen. Wir schieben die Funktion dennoch hier dazwischen und holen den Beweis gleich nach.

Was passiert also bei \(g_\Phi(i,x,t)\)?

1. \(\Phi_i(x)\) ist ja die kleinste Zahl \(t\), bei der \(h(i,n,t) \neq 0\) gilt, da \(\Phi_i(x)\) uns ja die Anzahl der Schritte liefert, die die Maschine \(\nu_M(\nu_P(i))\) braucht um bei der Eingabe  \(x\) zum Ende der Berechnung zu kommen.

2. \(\Phi_i(x)\) gibt es nur wenn es die Schrittzahlfunktion \(SZ(q_{oi},(\varepsilon,B,1^xB))\) und auch die Ausgabe \(\varphi_i(x)\) gibt. Ansonsten wäre sie nicht vorhanden: keine Ausgabe, keine Schritte, keine Standardkomplexität \(\Phi\).

3. Da \(h\) berechenbar ist (weisen wir gleich nach), auch Kompositionen aus den Funktionen berechenbar sind, so ist auch unsere charakteristische Funktion \(g_\Phi(i,x,t) = min(1,h(i,x,t))\) berechenbar.

Was \(min(1,h(i,x,t))\) sollte klar sein, ich schreibe es trotzdem mal auf:

Wir bekommen mit der Funktion \(min\) den kleinsten Wert aus der Auswahl von zwei Werten. Und wir haben die Auswahl zwischen \(1\) und dem Funktionswert von \(h(i,x,t)\).

Unser \(h\) gibt aber nur den Funktionswert zurück wenn die Maschine die Berechnung mit maximal \(t\) Rechenschritten abschließt, denn \(t\) ist die Anzahl der Schritte, die wir maximal rechnen dürfen. Ansonsten gibt es nur den Zonk, ähm, ich meine die \(0\). In diesem Fall hat die Maschine bereits \(t\) Schritte gerechnet und ist noch nicht bei der \(HALT\)-Marke angekommen, d.h. die Berechnung ist nach \(t\) Schritten noch nicht zu Ende.

Wir haben daher immer \(min(1,0) = 0\) wenn \(\Phi_i(x) > t\) oder \(min(1,Funktionwert)=1\) wenn \(\Phi_i(x)\leq t\). Passt.

Damit ist gewiesen, dass die Menge \(\{(i,x,t) \in \mathbb{N}^3\mid \Phi_i(x) \leq t\}\) tatsächlich rekursiv/entscheidbar ist, denn wir können entscheiden ob Maschine \(i\) bei der Eingabe von \(x\) nach \(t\) Schritten hält oder nicht.

Naja, streng genommen müssen wir dazu noch \(h\) als berechenbar nachweisen, aber das tun wir ja gleich im 3. Lernziel.

Und was ist mit der

Beispielaufgabe zu \(\omega_1 = (: R,1)(1:B,11,)\) von Oben?

Die holen wir mit dem Wissen, das wir haben nun nach. Hier noch einmal das Flussdiagramm damit Ihr nicht scrollen müsst:

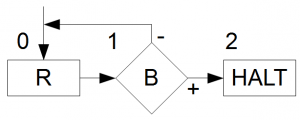
Wie viele Schritte braucht unser Flussdiagramm denn bei der Eingabe von z.B. \(1^3\), d.h. drei Einsen um bis zur \(HALT\)-Marke zu gelangen und wie sieht die Ausgabe dann aus? Spielt das Flussdiagramm einfach mal damit durch und Ihr werden feststellen, dass Ihr genau \(8\) Schritte braucht.

Bei der Eingabekonfiguration von \((0,(\varepsilon,B,1^3))\) kommen wir nach \(8\) Schritten dann bei der Endkonfiguration \((2,(1^3,B,\varepsilon))\) an. Wenn man das Flussdiagramm nun genauer betrachtet kommt man drauf, dass man bis zur Endkonfiguration genau \(2*3+2\) Schritte passiert hat. Bei der Eingabe von \(m\) Einsen muss man die Schleife \(m\) Mal passieren und führt so am Ende \(2m+2\) Schritte durch, was uns zu unserer Übergangsrelation führt:

\((0,(\varepsilon,B,1^m) \vdash^{2m+2} (2,(1^m,B,\varepsilon))\)

Und da \(\Phi_{n_1}(m)\) nun genau die Anzahl der Schritte ist bis die Maschine bei der Eingabe von \(m\) \(HALT\) erreicht, ist

\(\Phi_{n_1}(m) = 2m+2\)

Damit ist die Standardkomplexität \(\Phi_{n_1}\) zu \(\varphi(n_1)\) bei der Eingabe von \(m\) genau \(2m+2\). Würde die Maschine nicht halten, so wäre \(\Phi_{n_1} = div\).

Hiermit ist die Standardnummerierung für \(P^{(1)}\) abgehakt und wir kümmern uns jetzt um den Beweis von \(h\).

Antwort zum Lernziel: das \(\Phi\)-Theorem besagt drei Dinge:

• dass die Schrittzahlfunktion \(\Phi_i=SZ_i\) der Maschine \(i\) zu den einstelligen, berechenbaren Funktionen \(P^{(1)}\) gehört
• der Definitionsbereich von \(\Phi_i\) ist gleich dem Definitionsbereich von \(\varphi_i\), da beide Funktionen den selben Eingabeparameter \(x\) benötigen
• und die Menge \(\{(i,x,t)\in\mathbb{N}^3\mid \Phi_i(x) \leq t\}\) rekursiv/entscheidbar ist, da die charakteristische Funktion berechenbar ist.

Mit dieser Standardkomplexität können wir bestimmen wie viele Berechnungsschritte die Maschine \(i\) bei der Eingabe von \(x\) benötigt (\(\Phi_i(x)\)) oder feststellen ob die Maschine \(i\) bei der Eingabe von \(x\) nach \(t\) Berechnungsschritten hält oder nicht (\(g_\Phi(i,x,t)\)) um die Menge \((i,x,t)\in\mathbb{N}^3\) zu entscheiden.

Lernziel 3

Beweis der Berechenbarkeit von \(h:\mathbb{N}^3\rightarrow\mathbb{N}\)

Für die Formalisierung des utm-Theorems brauchen wir diese hilfreiche Funktion auch, also aufpassen! Definieren wir \(h\) zunäüchst:

\(h:\mathbb{N}^3 \rightarrow \mathbb{N}\)  mit

\(h(i,n,t) = \begin{cases} 1+\varphi_i(n), & \mbox{ falls } \Phi_i(n) \mbox{ existiert und } \Phi_i(n) \leq t\\ 0, & \mbox{ sonst }\end{cases}\)

Okay, dreistellige Funktion auf den natürlichen Zahlen, die ein einstelliges Ergebnis ausgibt. Wir bekommen eine \(1\) und das Ergebnis der Maschine \(\nu_M(\nu_P(i))\) bei der Eingabe von \(n\) wenn die Standardkomplexität \(\Phi_i\) existiert und kleiner/gleich \(t\) ist, d.h. wir kommen zum Ergebnis (\(HALT\)-Marke noch bevor wir \(t\) Rechenschritte absolviert haben). Ansonsten gibt es nur eine Null zurück. Fair.

Um zu beweisen, dass die Funktion \(h\) berechenbar ist wird wie folgt vorgegangen:

Wir zeigen, dass die Wortfunktion zu \(h\) berechenbar ist. Anhand der Standardnummerierung können wir ja Worte in Zahlen und Zahlen in Worte codieren. Unsere Wortfunktion wäre damit: \(\nu_\Sigma h\bar{\nu_\Sigma}^-1\).

Schaut euch die Standardnummerierung noch einmal an, falls euch das nicht mehr viel sagt. Anschließend basteln wir uns eine Turing-Maschine mit \(f_M=\nu_\Sigma h\bar{\nu_\Sigma}^-1\). Diese Funktion sieht dann so aus:

\(f_M(1^i,1^n,1^t) = 1^{h(i,n,t)}\)

\(1^{h(i,n,t)}=\begin{cases} 1^{1+\varphi_i(n)}, & \mbox{ falls } \Phi_i(n) \mbox{ existiert und } \Phi_i(n) \leq t\\ \varepsilon, & \mbox{ sonst }\end{cases}\)

Führen wir uns einfach mal vor Augen, dass die Turing-Maschine nur Eingaben in Form von \(1^x\), also \(x\) Mal die \(1\) entgegen nimmt und auch wieder ausgibt. Für die Funktion \(h\) wandeln wir unsere \(i, n\) und \(t\) daher einfach in die entsprechende Anzahl ein Einsen um (unäre Darstellung einer Dezimalzahl).

Während wir bei der Funktion \(h\) als Ergebnis dann \(1+\) den dezimalen Ausgabewert, also \(\varphi_i(n)\) bekommen hätten, bekommen wir hier einfach die dazu entsprechende Anzahl von Einsen (\(1^{1+\varphi_i(n)}\)); die unäre Darstellung des Ergebnisses. Das der Ausgabewert \(0\) jedoch nicht in unserem vorher definierten Alphabet für die Maschine ist, nutzen wir das leere Wort \(\varepsilon\) zur Codierung von \(0\).

Bevor ich hier den Beweis praktisch abschreibe, wäre es wahrscheinlich sinnig ihn direkt anhand eines Beispiels durchzuspielen. Wir nehmen wieder die Aufgabe aus dem ersten Teil:

Beispiel:  \((1^2:1,,1)(:1,1,1^2)(:B,,)\)

mit der zugehörigen Nummer \(n_1\), der willkürlichen Eingabe \( n=3\) und den maximal durchzuführenden Rechenschritten \(t=9\).

Ein Ergebnis sollten wir auch herausbekommen, da wir aus dem letzten Beitrag ja wissen, dass die Standardkomplexität \(\Phi_{n_1}(3)\) der Funktion ja \(8\) und bekanntlich ist \(8<9\) ist. Unser \(f_M\) sieht mit der willkürlichen Wahl der Eingangsparameter nun so aus:

\(f_M(1^{n_1},1^3,1^9) = 1^{h(n_1,3,9)}\)

\(1^{h(n_1,3,9)}=\begin{cases} 1^{1+\varphi_{n_1}(3)}, & \mbox{ falls } \Phi_{n_1}(3) \mbox{ existiert und } \Phi_{n_1}(3) \leq 9\\ \varepsilon, & \mbox{ sonst }\end{cases}\)

Wir haben folgende Teil-Flussdiagramme mit den entsprechenden Aufgaben:

• \(F_1\): Transformiert die Eingabe auf die einzelnen Bänder (siehe unten).
• \(F_2\): Kopiert die Anfangsmarke auf Band \(4\).
• \(F_3\): Sucht auf Band \(1\) nach dem Befehl mit der Marke von Band \(4\). Wird keine passende Marke auf Band \(1\) gefunden, so muss es eine \(HALT\)-Marke sein.
• \(F_4\): Simuliert den gefundenen Befehl von Band \(1\) auf dem Band \(2\), wo unser Eingabewort steht.
• \(F_5\): Testet ob weitergerechnet werden darf, d.h. ob noch Einsen auf Band \(3\) stehen.
• \(F_6\): Subtrahiert eine Eins von Band \(3\) bei jedem simulierten Rechenschritt von \(F_4\).
• \(F_7\): Kopiert vom Arbeits- und Eingabeband \(2\) am Ende alle Einsen auf Band \(0\) und erzeugt uns so auf dem gewünschten Band \(0\) eine Ausgabe.

Wir transformieren die Eingabecodierung \(EC(1^{n_1},1^3,1^9 )\) und setzen jeden der drei Parameter als ein Eingabewort aus Einsen auf ein eigenes Band. Was jedoch mit \(1^{n_1}\) gemacht wird, ist etwas spannender: Aus \(1^{n_1}\) wird \(\nu_P(n_1)\), unser Bandprogramm aus \(BP\) (zur Auffrischung: siehe Lernziel 1), welches nun auf Band \(1\) unserer Maschine steht.

Auf Band \(2\) (Eingabeband) steht die Eingabe \(1^{3}\) (\(n=3\)). Auf diesem Band werden die einzelnen Berechnungsschritte von Band \(1\) (dem Programmband) simuliert. Band \(3\) (Schrittzahlband) ist der Schrittzähler mit \(1^9\), wo bei jedem Schritt von \(\nu_P(n_1)\) eine \(1\) gelöscht wird. Auf Band \(4\) (Markenband) wird die aktuelle Marke gespeichert. Unsere Bänder sehen nun so aus:

Das hat unser Teil-Flussdiagramm \(F_1\) gemacht. Nun kommt \(F_2\) und kopiert die Anfangsmarke nach Band 4:

Nun sucht Teil-Flussdiagramm \(F_3\) auf Band \(1\), wo unser Programm gespeichert ist das erste Teilwort, wo die gespeicherte Marke von Band \(4\) vorkommt. Wenn es einen passenden Befehl findet, führt Teil-Flussdiagramm \(F_4\) den Befehl auf Band \(2\) aus. Wenn nicht, so ist es eine Endmarke (wir erinnern uns an den ersten Abschnitt: wenn im Programm auf eine Marke referenziert wird, es jedoch keine Beschreibung für diese gibt, so ist es eine \(HALT\)-Marke).

Da die Marke \(1^2\) von \(F_3\) gefunden wird, wird der Befehl auf Band \(2\) von Teil-Flussdiagramm \(F_4\) ausgeführt. Wenn er die Form \((1^k:\beta,1^n)\) hat, wird die Bandoperation \(\beta\) auf Band \(2\) ausgeführt und die gespeicherte Marke auf Band \(4\) mit der Folgemarke \(1^n\) ersetzt. Hat der Befehl die Form \((1^k:\beta,1^j,1^m)\), so testet \(F_4\) ob unter dem Kopf \(\beta\) steht und ersetzt die Marke auf Band \(4\) entsprechend dem Ergebnis durch \(1^j\) (nein, \(\beta\) steht nicht unter dem Lesekopf) oder \(1^m\) (ja, \(\beta\) steht unter dem Lesekopf). Das Teil-Flussdiagramm \(F_5\) prüft ob auf dem Zählerband \(3\) noch Einsen stehen, d.h. ob weitergerechnet werden kann.

In unserem Fall sehen unsere Bänder anschließend so aus, da der Befehl \((1^2:1,,1)\) auf Band \(1\) gefunden und ausgeführt wurde. Auch ist eine \(1\) auf Band \(2\) unter dem Lesekopf, so dass wir nicht in die Marke \(1\), sondern in die „leere“ Folgemarke springen werden und diese Folgemarke auf unser Folgemarkenband \(3\) schreiben. Auch haben wir eine \(1\) von unserem Zählerband, Band \(4\) mit dem Teil-Flussdiagramm \(F_6\) gelöscht.

Da noch Einsen auf dem Zählerband stehen (\(F_5\) hat das geprüft), dürfen wir weiterrechnen. Nun wird nach der „leeren“ Marke auf Band \(1\) gesucht, diese auf Band \(2\) durch \(F_4\) ausgeführt, wieder eine \(1\) vom Zählerband \(3\) durch \(F_6\) gelöscht, die Folgemarke auf Band \(4\) durch \(F_4\) geschrieben, diese wieder auf Band \(1\) durch \(F_3\) gesucht, usw.

Wir wiederholen den Spaß nun die ganze Zeit bis die Maschine letztendlich alle ihre Befehle abgearbeitet (es in einem befehl auf eine Marke referenziert, diese auf das Folgemarkenband geschrieben und gesucht. Sie steht aber nicht auf Band \(1\) – es ist also eine Endmarke) hat. Dann geht es von \(F_3\) zu \(F_7\), welches die Ausgabe von Band \(2\) auf Band \(0\) kopiert. Wäre es keine Endmarke, würde von \(F_5\) noch einmal geprüft werden ob noch Einsen auf dem Zählerband stehen. Wenn das nicht der Fall wäre, so würde die Maschine halten. In unserem Fall sind noch Einsen auf Zählerband, eine Endmarke ist aber erreicht worden, alles ist gut.

Um noch wie gewünscht die \(1\) zur Ausgabe \(1^{\varphi_{n_1}(1^3)}\) zu addieren und den Lesekopf rechts von der Ausgabe zu positionieren werden am Ende noch die Befehle \(0:1\) und \(0:R\) ausgeführt.  Am Ende sehen unsere Bänder wie folgt aus:

Die gesuchte Ausgabe steht auf dem Ausgabeband \(0\).

Damit haben wir die Berechenbarkeit der Funktion \(h\) bewiesen. Und damit wir die ganze Arbeit nicht umsonst gemacht haben, nutzen wir \(h\) gleich für das smn- un das utm-Theorem.

Antwort zum Lernziel: Um die charakteristische Funktion \(g_\Phi\) für das \(\Phi\)-Theorem zu berechnen, ist es notwendig die Maschine mit der Nummer \(i\) auf einer (sog. universellen) Turingmaschine zu simulieren.

Dazu wird das zu simulierende Bandprogramm \(\nu_P(i)\), die Eingabe \(x\), die maximale Anzahl der Schritte \(t\) auf jeweils ein Band der neuen Maschine geschrieben und die einzelnen Befehle des Bandprogramms \(\nu_P(i)\) auf dem Eingabeband, wo \(x\) steht simuliert. Bei jedem Berechnungsschritt wird \(t\) auf dem Schrittzahlband um Eins dekrementiert, während auf dem Markenband sich die Marke des aktuell zu simulierenden Befehls befindet damit die simulierende Maschine immer weiß, wo sie gerade ist.

Endet die Berechnung noch bevor \(t\) auf dem Schrittzahlband zu \(0\) geworden ist, war die Berechnung erfolgreich und es ist \(h\neq 0\). Ist auf dem Schrittzahlband jedoch bereits \(t=0\), so wird die Berechnung abgebrochen und es gilt \(h=0\). Damit braucht die Maschine \(i\) bei der Eingabe von \(x\) mehr Berechnungsschritte als \(t\) um zur Endmarke \(HALT\) zu gelangen.

Diese Funktion ist nicht nur für das \(\Phi\)-Theorem wichtig, sondern bildet auch die Basis einer universellen Turingmaschine.

Weil der Beitrag zu den letzten drei Lernzielen so lang geworden ist, geht der Rest im nächsten Beitrag weiter.