TIA: Turing-Maschinen, Hilfssymbole (Lernziele KE3, Update 3)

Update 3: Nach Olivers Einwand (Danke hier nochmal!) habe ich den Abschnitt über Hilfssymbole erneut überarbeitet.

Update 2: Wow, beim Durchgehen des Eintrags sind mir massive Schnitzer bei den Hilfssymbolen aufgefallen. Hoffentlich sind die jetzt raus. Sorry!

Update: mit dem Eintrag sollten nun alle Lernziele aus KE3 erschlagen worden sein. Ist zwar etwas lang geworden, aber vielleicht hilft es dem ein oder anderen beim Verständnis. Die neuen Erkenntnisse z.B. bzgl. der Hilfssymbole entstammen dem Mentoriat in Hagen mit Herr Dr. Halbach. Ich kann nur ausdrücklich raten diese Mentoriate in Anspruch zu nehmen und auch immer Fragen zu stellen wenn einem etwas nicht klar sein sollte.

Habe bei vielen Mentoriaten gesehen, dass die Leute auf die fragenden Blicke des Mentors 2 Stunden lang immer nur fleißig nicken. Nach dem Mentoriat schaut man trotzdem in die gleichen, ratlosen Gesichter ein stückweit mehr resignierter Komillitonen. Also fragen bis es "Klick!" macht. Auch sind viele Mitstudenten gerne bereit es einem auch mit anderen Worten zu erläutern. Nur keine Scheu, sitzen doch alle im selben Boot 😉

Einleitung

Aber fangen wir an: während in der Literatur zunächst Einband-Maschinen eingeführt werden um sie dann durch Mehrbandmaschinen zu ersetzen wird das in dem Kurs an der FU hier genau anders rum gemacht (wie vieles andere im Skript auch...). Auch werden die Turing-Maschinen oft als 7-Tupel definiert, im Skript haben wir ein 5-Tupel. Solche Dinge machen es - meiner Meinung nach - dem Leser unnötig schwer sich den sehr wichtigen Stoff zu erarbeiten.

Anstatt dass man vielleicht in Zusatzliteratur einen Sachverhalt in anderen Worten verständlicher nachlesen kann, muss man die Definitionen erst in die Definitionen des Skripts überführen. Dafür muss man aber zuerst verstehen, was im Skript denn steht. Hierfür hat man sich aber speziell die Zusatzliteratur besorgt. Da beißt sich die Katze in den Schwanz.

Ich möchte hier versuchen bei der Definition des Skripts zu bleiben und die Parallelen zur "üblichen" Definition zu ziehen damit man auch mit Fremdliteratur arbeiten kann. Ebenso würde ich auch lieber mit Einbandmaschinen starten, statt wie im Skript sofort Mehrbandmaschinen einzuführen um diese dann durch Einbandmaschinen zu ersetzen...

Darstellungsweise: Zunächst jedoch zur Darstellungsweise. Am häufigsten wird die unäre Darstellungsweise für Turingmaschinen verwendet, d.h. eine 5 auf dem Eingabe- oder Ausgabeband besteht aus fünf Einsen $(11111)$. Die binäre Darstellung ist zwar etwas hübscher und in einigen Bereichen durchaus sinnvoll, aber die Formulierung von Algorithmen ist mit der unären Darstellungsweise meist einfacher.

Einbandmaschinen

Im Gegensatz zu Mehrbandmaschinen besitzt diese nur ein einziges Band, welches als Ein- und Ausgabe- sowie Arbeitsband dient. Die Eingabeworte befinden sich hier zu Beginn rechts von Lesekopf und sind nur Trennzeichen getrennt. Links befindet sich die Ausgabe. Während der Berechnung wird die Eingabe dann durch die Ausgabe ersetzt, d.h. gelöscht. Am Ende steht das Ergebnis links vom Kopf.

Im Skript sind die Einbandmaschinen definiert als:

$M=(F,(\Sigma^*)^k,\Sigma^*,EC^{(k)},AC)$

Wir erklären den Spaß hier einfach mal:

• $F$: das Flussdiagramm der Maschine, in der Literatur werden hier oft Zustände und Überführungsfunktionen verwendet
• $(\Sigma^*)^k$: die Menge aller Wörter mit k Elementen über $\Sigma$. k ist hier wieder die Stelligkeit. Statt einem Zeichen, können wir k auch Zeichen lesen. Ist z.B. das Alphabet $\Sigma^* = \{b,a,c\}$, so wäre $(\sum^*)^2 = \{ba,bb,bc,ab,aa,ac,ca,cb,cc\}$ und $"aa" \in (\Sigma^*)^2$.
• $\Sigma^*$: eben das gerade vorgestellte $\sum^*$, d.h. das Alphabet.
• $EC^{(k)}$: die ggf. k-stellige Eingabecodierung auf dem Band, d.h. die Worte, die durch ein Trennzeichen getrennt rechts vom Lesekopf stehen. Dieses Trennzeichen wird in der Literatur oft als ein Teil im Tupel angegeben. In Wikipedia wird z.B. ein Quadrat als Trennzeichen verwendet. Im Skript ist es ein einfaches $B$ für Blank. Sie sieht dann z.B. so aus: $EC^{(3)}(ab,ac,aa) = (\varepsilon,B,abBacBaa)$
• $AC$: die Ausgabecodierung am Ende einer Berechnung, welches links vom Lesekopf ist und nur Symbole aus $\Sigma$ hat. D.h. man ließ meist einfach zurück bis zum ersten Trennzeichen.

Zusätzlich dazu werden die möglichen Operationen definiert:

• gehe ein Feld nach links
• gehe ein Feld nach rechts
• schreibe a direkt unter den Lesekopf
• prüfe ob a unter dem Lesekopf steht

Das $\Gamma$ wird im Skript als Arbeitsalphabet bezeichnet. D.h. es ist $\Gamma := \Sigma \cup \{B\}$, also alle Symbole des Alphabets $\Sigma$ und das Trennzeichen $B$. Diese werden dann auf dem Band verwendet. Zusätzlich dazu werden in der Literatur und in der Wikipedia Zustände (Anfangs- und Endzustand) und Marken, sowie eine Überführungsfunktion definiert.  In unserer Definition ist die Überführungsfunktion das Flussdiagramm, wo auch unsere Zustände (Marken) drin sind. Einfach merken: $\Sigma$ = komplettes Alphabet ohne Trennzeichen, $\Gamma$ = Bandalphabet mit Trennzeichen.

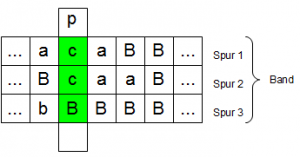
Mit $\beta$ wird im Skript die Funktion bezeichnet, die uns ein Zeichen auf dem Band ausgibt: $\beta(0)$ ist das Zeichen unter dem Lesekopf, $\beta(m)$ das Zeichen auf dem m-ten Feld rechts davon, $\beta(-m)$, auf dem Feld links davon sein. Im folgenden Bild (p ist der Lesekopf) ist z.B. $\beta(0)=t$, $\beta(-2)=f$ und $\beta(1)=b$ auf einem Band.

Die folgenden Ausführungen basieren nicht auf dem Skript, sondern auf dem Buch von Dirk W. Hoffmann. Die Symbole $\Gamma$, $\Gamma^{*}$ sind minimal anders belegt.

Für die Ausführungen zum Hilfssymbollemma unten, geht Ihr bitte wieder von der Definition im Skript aus.

Mehrspurmaschinen

Zwar wird das im Skript nicht so explizit erwähnt, aber wir reden hier auch über Mehrspurmaschinen. D.h. man hat zwar $k$ Spuren, aber nur einen Lese- und Schreibkopf und somit auch nur ein Band und damit eine $k$-stellige Einbandmaschine. Wir können nur, bei z.B. 3 Spuren, das Tripel lesen. Die $k$ Eingabeworte der Einbandmaschine, welche nur durch ein Trennzeichen getrennt sind, finden sich bei der Mehrspurmaschine nun in $k$ Spuren wieder. In jeder Spur befindet sich somit ein Eingabewort.

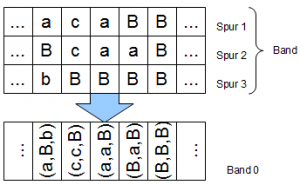
Haben wir z.B. folgende Belegung auf den Spuren mit dem Alphabet $\Sigma = \{a,b,c\}$ und dem Arbeitsalphabet $\Gamma = \{a,b,c,B\}$:

So lesen wir $(c,c,B)$ wenn der Lesekopf über der 3. Spalte steht. Wir haben keine 3 Leseköpfe, die wir justieren könnten und müssen das vollständige Band bewegen. Solche Maschinen lassen sich leicht durch Einbandmaschinen simulieren, indem wir das Alphabet $\Sigma$ auf $\Sigma^3$ erweitern und fortan $(c,c,B)$ ein Element, also ein einzelnes Zeichen, aus unserem neuen Alphabet $\Sigma^3$ auf einem einzigen Band ist, d.h. alle Tripel aus den Zeichen a, b, c und dem Blank B bestehen. Damit blähen wir das Alphabet natürlich deutlich auf. Die Restriktion mit den sich nicht bewegenden Köpfen werden wir in den Mehrbandmaschinen entfernen.

Die Mehrspurmaschine mit $k$ Spuren können wir also durch eine $k$-stellige Einbandmaschine simulieren:

Die Restriktion mit den sich nicht bewegenden Köpfen werden wir in den Mehrbandmaschinen entfernen.

Mehrbandmaschinen

Die Mehrbandmaschine besitzt, ähnlich zu den Registermaschinen, folgende Grundfunktionen (welche mittels eines Flussdiagramms und so auch mittels einer Registermaschine nachgebildet werden können):

• gehe auf Band i ein Feld nach links
• gehe auf Band i ein Feld nach rechts
• schreibe a auf Band i direkt unter den Kopf
• prüfe ob a unter dem Lesekopf auf Band i ist

Ausgabeband ist das Band mit der Nr. 0, Bänder $1-k$ sind Eingabebänder. Auf jedem Eingabeband steht eines der $k$ Worte. Man sieht hier sofort, dass wir nun bewegliche Leseköpfe haben, da sie sich auf den unterschiedlichen Bändern unabhängig voneinander bewegen können. Wir können fortan Operationen auf einem Band unabhängig von den anderen Bändern durchführen.

Merksatz: Einbandmaschinen haben nur ein einziges Band, welches als Ein- und Ausgabeband dient. Dort stehen die $k$ Worte durch ein Trennzeichen getrennt auf dem einzigen Band. $k$-stellige Einbandmaschinen können Mehrspurmaschinen mit $k$ Spuren simulieren. Mehrspurmaschinen haben zwar auch nur ein Band, welches jedoch in $k$ Spuren unterteilt ist. Hier gibt es keine beweglichen Lese-/Schreibköpfe. Mehrbandmaschinen verfügen über mehrere Bänder, die sich unabhängig von einander bewegen können und somit über bewegliche Lese-/Schreibköpfe verfügen. 

Lange Rede, kurzer Sinn: Mehrspurmaschinen mit $k$ Spuren können durch das Aufblähen des Alphabets mit $k$-stelligen Einbandmaschinen simuliert werden. Mehrbandmaschinen können wiederum durch Mehrspurmaschinen simuliert werden und letztendlich in eine $k$-stellige Einbandmaschine überführt werden. Dabei werden Markierungen (in der Literatur sind es oft zusätzliche Spuren) der Zeichen für die Position des virtuellen Lese-/Schreibkopfs pro Spur verwendet. 

Beweis der Berechnungsstärke

Die Mehrband-, Mehrspur- und die Einbandmanschinen haben die gleiche Berechnungsstärke. D.h. wir können Mehrbandmaschinen (mit beweglichen Leseköpfen) mit $k$ Bändern durch Mehrspurmaschinen simulieren. Die Mehrspurmaschinen können als Einbandmaschinen formuliert werden. Den Lernzielen nach sollte man den Beweis nachvollziehen und seine Grundidee erläutern können. Der Beweis im Skript basiert auf der gleichen Grundidee, visualisiert die Darstellung der beweglichen Köpfe jedoch sehr bescheiden. Ich werde die Idee des Skripts am Ende aber dennoch kurz skizzieren. Für das Verständnis halte mich aber erstmal an die Zusatzliteratur.

Falls jemand etwas findet, der den Beweis im Skript verständlicher formuliert als das Skript selbst: bitte melden!

Mehrspurmaschine als Einbandmaschine

Hier wollen wir aus einer $k$-stelligen Einbandmaschine (es ist ja ein einziges Band, die Stelligkeit wird aber in "Spuren" dargestellt. Ggf. gibt es noch ein Ausgabeband 0) eine $k$-stellige Turingmaschine mit einem Band (ohne Spuren) basteln. Ist ja kein Problem, da wir hier einfach nur das Alphabet aufblähen müssen. Die Operationen bleiben fast gleich, nur dass sie jetzt nicht auf Spuren, sondern auf einem $k$-Tupel operieren.

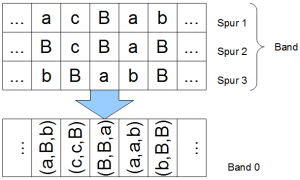
1. Als erstes die Anpassung der Eingabe: man kopiert alle Eingabeworte der $k$ Spuren auf das Ausgabeband der Maschine. Beispiel: siehe folgendes Bild.
2. Die Funktionen "L", "R", "a", "a?" werden dann durch "0:L", "0:R", "o:a" und "0:a?" ersetzt, da sie nun nur auf Ausgabeband 0 durchgeführt werden.

Damit haben wir eine $k$-stellige Bandmaschine (bei $k > 1$ auch Mehrspurmaschine genannt) mit einer $k$-stelligen Turingmaschine und nur einem einzigen Band simuliert. Die unbeweglichen Leseköpfe machen es uns hier einfach.

Mehrbandmaschine als Mehrspurmaschine

Und nun anders herum, was etwas schwieriger ist: die Konstruktion einer $k$-stelligen Einbandmaschine (also nur ein Band, aber $k$ Spuren), welche die selbe Funktion der Mehrbandmaschine mit $k$ Bändern berechnet:

Soweit so unklar. Wir haben hier das Problem der beweglichen Leseköpfe. Während wir bei der Mehrbandmaschine oben die Leseköpfe auf dem 2. Feld in Band 1 (a) und auf dem 3. Feld in Band 2 (a) haben könnten, können wir das auf unserer Einbandmaschine aber nicht darstellen. Was also tun? In der Literatur wird hierfür für jedes Band eine neue Spur erstellt, welche alle unterschiedlichen Positionen der Leseköpfe auf dem Band darstellt. Wir tun also folgendes:

1. wir speichern die Position der Leseköpfe einer Spur (Datenspur) auf einer zusätzlichen Spur (Positionsspur).
2. wir erweitern unser Bandalphabet $\Gamma$ in ein neues: unser $\Gamma^{*}$. Zusätzlich zu den Einzelsymbolen im Bandalphabet $\Gamma$ werden dann alle Kombinationen der Zeichen auf den Bändern hinzugefügt.
3. wir simulieren den Befehl für Band $i$ auf unserer Spur $i$.

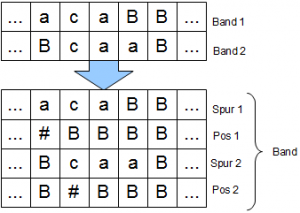
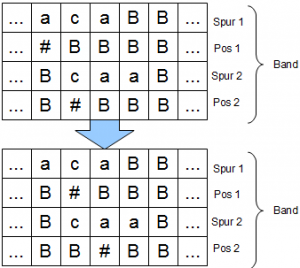
Im oberen Bild sind die Leseköpfe für Band 1 und 2 auf den ersten Eingabeworten positioniert. Wie ist nun der Ablauf? Zunächst befindet sich das Band ganz am Anfang, d.h. es steht ein $B$ auf jeder Spur (auch wenn ich das $B$ in der ersten Spur/im ersten Band im Bild oben unterschlagen habe, zu faul ein neues zu malen). Wir haben nun z.B. einen Befehl, der auf Band 1 das erste $a$ durch den Wert ersetzen soll, der unter dem Lesekopf auf Band 2 steht. Anschließend soll auf beiden Bändern ein Schritt nach rechts gemacht werden.

Da wir die Leseköpfe nicht mehr unabhängig von einander bewegen können, wird das Band nach rechts gespult bis die beiden Positionsmarkierungen für Spur 1 und 2 gefunden wurden. Die Werte merkt sich die Maschine und führt nun den Befehl statt auf Band 1 nun auf Spur 1 aus. Anschließend werden die Positionsmarkierungen wie gewünscht auf beiden Bändern um eins nach rechts verschoben. Das folgende Bild visualisiert diese Operation auf dem Band.

Soll der nächste Befehl durchgeführt werden, so wird das Band wieder nach rechts gespult bis die Positionsmarkierungen gefunden wurden, der Befehl ausgeführt und die Positionsmarkierungen erneut verschoben. Am Ende steht das Ergebnis auf der 1. (oder einer speziell dafür vorgesehenen) Spur links vom Lesekopf und das Band muss nur noch zurückgespult werden.

Skriptbeweis

Der Beweis im Skript verwendet keine zusätzlichen Spuren, sondern markiert das Zeichen, über welchem der Kopf steht mit einem Querstrich, z.B. $\overline{a}$.  Damit werden z.B. aus dem Symbol $(1,0)$ in der Mehrbandmaschine, wo der Kopf auf $1$ oder $0$ stehen kann nun die folgenden Symbole: $(1,0), (\overline{1},0), (1,\overline{0}), (\overline{1},\overline{0})$ für die Positionierung der virtuellen Leseköpfe. Damit haben wir eine massive Vergrößerung unseres Bandalphabets.

Das Gleiche haben wir im Beweis von oben. Überführen wir die Mehrspur- nun in eine Einbandmaschine, so ist unser Alphabet ebenfalls erweitert: aus $(a,B)$ wird dann $(a,B,b,B), (a,\#,b,B), (a,B,b,\#), (a,\#,B,\#)$.

Alles in allem: die Simulation der Mehrband- in einer Einbandmaschine erfolgt auf Basis eines vergrößerten Alphabets für die Darstellung der Position der Leseköpfe auf den simulierten Bändern.

Beweis der Turing-Berechenbarkeit von Funktionen

Um zu beweisen, dass eine Funktion von der Turingmaschine berechnet wird tut man das gleiche, was man bereits bei Registermaschinen getan hat. Man behauptet, dass das aufgestellte Flussdiagramm (oder die Zustandsübergangstabelle) genau das tut und von einer gegebenen Eingabecodierung auf die gewünschte Ausgabecodierung führt.

Anschließend werden mittels vollständiger Induktion Annahme und Behauptung aufgestellt und das Flussdiagramm entsprechend oft durchgespielt. Am Ende muss dann die Behauptung rauskommen. Man sollte nicht vergessen alle Eingabefälle durchzuspielen.

Schaut dazu einfach mal in den Beitrag für die Einzelschrittfunktion und den Beweis der Addition mittels vollständiger Induktion.

Hilfssymbole

Den Lernzielen nach sollte man den Beweis verstehen, dass man auch ohne Hilfssymbole auskommt. Wir wir oben gesehen haben müssen wir das Alphabet massiv erweitern wenn wir eine Mehrbandmaschine durch eine Mehrspur- und dann durch eine Einbandmaschine simulieren wollen. Diese zusätzlichen Symbole, welche nicht in dem ursprünglichen Arbeitsalphabet inkl. dem Trennzeichen $B$ drin sind werden Hilfssymbole genannt.

Verwendet man wie im Skript-Beweis für die Kopfpositionen markierte Zeichen statt $\#$, so müssen wir diese markierten Zeichen ($\overline{1}$ z.B.) mit in das neue Arbeitsalphabet nehmen. Aber nicht die einzelnen Zeichen, sondern Kombinationen davon.

Beispiel

Besteht unser Alphabet nur aus $\Sigma := \{a,b\}$, unser Arbeitsalphabet somit aus  $\Gamma := \{a,b,B\}$ und wir simulieren unsere Mehrbandmaschine mit $2$ Bändern durch eine Einbandmaschine, so haben wir eine massive Erweiterung unseres Arbeitsalphabets: Ds neue Alphabet $\Gamma^{'}$ ist eine Kombination aus $\Gamma^{'}=\Gamma\cup(\Gamma\cup\overline{\Gamma})^l$, wobei $l$ die ursprüngliche Anzahl der Bänder ist.

Konkret

Haben wir unser $\Gamma := \{a,b,B\}$ und $2$ Bänder, die wir zusammenschmelzen müssen, so sieht unser $\Gamma^{'}$ wie folgt aus:

$\begin{array}{ll}\Gamma^{'}&=\{a,b,B\}\cup(\{a,b,B\}\cup\{\overline{a},\overline{b},\overline{B}\})^2\\{}&=\{a,b,B\}\cup(\{a,b,B,\overline{a},\overline{b},\overline{B}\}\times\{a,b,B,\overline{a},\overline{b}\overline{B}\})\\{}&=\{a,b,B,aa,ab,aB,...,\overline{B},\overline{B}\}\end{array}$

Aus $3$ Zeichen unseren Urspungs-Bandalphabets sind nun insg. $39$ neuen Zeichen geworden.

Achtung: seht z.B. $a\overline{B}$ nicht als Kombination von $a$ und $\overline{B}$ an, sondern als einzelnes Zeichen. Wir verwenden $a\overline{B}$ weil es leichter lesbar ist, wir hätten auch ein chinesisches Schriftzeichen dafür verwenden können, denn es ist wirklich nur ein einzelnes Zeichen aus unserem neuen Arbeitsalphabet $\Gamma$.

Anstatt, dass nun Worte mit $\{a,b,B\}$ auf unserem Band stehen, bestehen sie aus $\{a,b,B,aa,ab,aB,...,\overline{B},\overline{B}\}$.

Mit zwei Bändern uns zwei Zeichen haben wir bereits $39$ neue Zeichen. Mit drei Bändern hätten wir $219$, mit vier bereits $1299$. Etwas viel, nicht? Was können wir dagegen tun? Das Hilfssymbollemma anwenden!

Wie werden wir die neuen Zeichen wieder los? Kommen wir denn nicht mit unserem ursprünglichen Arbeitsalphabet aus? Doch! Wir codieren mit den Zeichen aus unserem Ursprungsalphabet einfach unsere insg. $39$ Zeichen des neuen Arbeitsalphabets.  Wie? Wir variieren einfach die Länge!

Wie viele Kombinationen der Zeichen aus dem Alphabet $\Sigma$ bekommen wir mit der Länge $1$ dargestellt? Genau $2^1$: $a,b$. Und Länge 2? Genau $2^2$: $aa,ab,ba,bb$. Welche Länge brauchen wir um unsere $39$ Zeichen darstellen zu können? Für die Darstellung der Zahl $39$ in binär reichen uns $6$ Bit, also $2^6=64$ ($2^5=32$ wäre uns zu klein).

Also wählt euer $m$ für die Länge $n^m$ ($n$ ist die Anzahl der Zeichen im Ursprungs-Zeichensatz) entsprechend, damit ihr mindestens so viele Kombinationen aus den Zeichen aus $\Sigma$ habt um eure alten und neuen Symbole damit zu codieren.

Wir brauchen das riesen Arbeitsalphabet mit den Hilfssymbolen damit nicht mehr und bleiben durch die neue Form der Codierung bei geschmeidigen $\{a,b,B\}$. Nur die Länge ist halt ein Stück größer geworden. Eine willkürliche Codierung der $39$ Symbole unseren ursprünglich aufgeblasenen Bandalphabets würde z.B. so aussehen können:

$a\rightarrow aaaaaa$

$b\rightarrow bbbbbb$

$B\rightarrow aaaaab$

$aa\rightarrow aabbbb$

$ab\rightarrow aaabbb$

$aB\rightarrow aaabba$

$a\overline{a}\rightarrow aabaaa$

$a\overline{b}\rightarrow abbaaa$

$...$

$\overline{B}\overline{B}\overline{B}\rightarrow ababab$

Done.

Wir können also beliebige Zeichen mittels nur zwei Symbolen codieren. Genau das besagt das Hilfssymbollemma:

Zu jeder Bandmaschine $M$ mit Ein/Ausgabealphabet $\Sigma$ gibt es eine Bandmaschine $M^{'}$ mit dem Arbeitsalphabet $\Gamma^{'}=\Sigma\cup\{B\}$, so dass $f_M=f_{M^{'}}$ gilt.

Wahrscheinlich ist euch noch nicht ganz klar, warum das so wichtig ist.

Es ist eig. ganz einfach: Wir haben uns hier auf $a$ und $b$ als Ein/Ausgabealphabet versteift. Wir können aber auch $\Sigma=\{1,0\}$ nehmen. Nun können wir mit dem Lemma beliebige Zeichen eines Arbeitsalphabets auch mittels $1$ und $0$ codieren und uns nur noch darauf beschränken. Ab hier übernehmen dann unsere Computer, denn sie kennen nur Strom an ($1$) und Strom aus ($0$).

Fazit: damit haben wir nun alle Lernziele aus der Kurseinheit durch. Wer noch Fragen hat oder grobe Schnitzer findet: ab in die Kommentare!

Datum: 4. November 2012
Kategorie: Theoretische Informatik
Kommentarfeed: RSS 2.0 • Trackback: Trackback-Url