Autor: Anton

Update 3: Korrektur nach Einwand von Phil. Finde ich super, dass Ihr nach fast 3 Jahren immer noch Fehler aufspürt und in den Kommentaren helft, die zu entfernen. Danke!

Update 2: Bitte Kommentar von Steve beachten. Grafik habe ich nun ersetzt (Marke 9 hinzugefügt), aber die Punkte für die „Endlosigkeit“ der Bänder in den Beispielen müsst Ihr euch noch dazu denken. Auf die habe ich der Übersichtlichkeit halber (ja, nur der Übersichtlichkeit wegen! Gegen den Einwand, dass meine Schreibfaulheit daran Schuld wäre, wehre ich mich entschieden(!)) in den Beispielen verzichtet 😉

Update: Flussdiagramm Lernziel 2 abgeändert. Danke Basti!

Nun kommen wir zu den Turing- und Bandmaschinen.

Wir nähren uns also der Essenz des ersten Teils der theoretischen Informatik. Die folgenden Beiträge wurden für diese Kurseinheit bereits erstellt und sind in den passenden Lernzielen entsprechend verlinkt.

• Turing-Maschinen, Hilfssymbole und Lernziele KE3

Ich empfehle daher sich einfach mal entlang dieses Beitrags zu hangeln und die Details dann entsprechen der Verlinkung aus dem anderen Beitrag zu holen.

Lernziel 1

Erläuterung der Definition einer Turingmaschine

Das, was im oben verlinkten Beitrag steht, fassen wir hier noch einmal kurz zusammen, da wir dort nur die Einbandmaschine im Detail beschrieben haben.

Die Turingmaschine (Mehrbandmaschine) ist definiert als:

\(M=(F,(\Sigma^{*})^k,\Sigma^{*},EC^{(k)},AC)\)

• Das \(F\) der Turingmaschine ist unser Flussdiagramm
• \((\Sigma^{*})^{k}\) sind unsere beliebig langen \(k\) Worte über dem Alphabet \(\Sigma\), welche später auf die \(k\) Bänder geschrieben werden.
• Die Turingmaschine operiert auf unendlichen Folge von Bändern als Datenspeicher mit dem darauf verwendeten Arbeitsalphabet \(\Gamma\).
• Die Turingmaschine hat folgende Eingabecodierung: \(EC^{(k)}:(\Sigma^{*})^k\rightarrow D\), definiert als
  \(EC^{(k)}(x_1,…,x_k):=((\epsilon,B,\epsilon),(\epsilon,B,x_1),…,(\epsilon,B,x_k),(\epsilon,B,\epsilon))\)
  Das bedeutet nichts anderes, als dass wir jedes Eingabewort auf jeweils ein Band schreiben und alle anderen Bänder leer sind.
  Beispiel: \(EC^{(3)}(aaa,b,bba):=((\epsilon,B,\epsilon),(\epsilon,B,aaa),(\epsilon,B,b),(\epsilon,B,bba),…,(\epsilon,B,\epsilon))\)
  Initial steht also der Lesekopf über dem ersten Blank.
• Die Turingmaschine hat folgende Ausgabecodierung \(AC\): das längste Wort auf Band \(0\) , welches direkt links vom Lesekopf steht und nur Zeichen aus dem Alphabet \(\Sigma\) beinhaltet. Lesen wir die Ausgabe also zurück, so stoppen wir beim \(B\); die bis dahin gelesenen Zeichen sind unsere Ausgabe.
• Die Turingmaschine besteht nur aus folgenden Befehlen:
  • \(i:L\) Lesekopf auf Band \(i\) ein Feld nach links
  • \(i:R\) Lesekopf auf Band \(i\) ein Feld nach rechts
  • \(i:a\) Schreibe auf Band \(i\) das Zeichen \(a\) unter den Kopf
  • \(i:a?\) Teste auf Band \(i\), ob das Zeichen \(a\) unter dem Kopf steht

Achtung: sollte bei einer Links- oder Rechtsbewegung dann plötzlich ein \(\epsilon\) unter dem Lesekopf stehen, wird ein Blank \(B\) daraus, da \(\epsilon\) nicht zum Alphabet gehört.

Der Einwand vom Phil in den Kommentaren ist berechtigt. \(\epsilon\) gehört nicht zum Alphabet und wird nur für die Darstellung als Tripel \((u,v,w)\) benutzt (siehe letzter Kommentar).

Ist doch nicht so schwer, oder. Beispiel?

Beispiel: Turingmaschine \(M=(F,(\Sigma^{*})^k,\Sigma^{*},EC^{(k)},AC)\)

Alphabet \(\Sigma=\{1,0\}\), besteht nur aus \(1\) oder \(0\)

Anzahl der Arbeitsbänder und somit auch unserer Worte: \(k=2\)

Arbeitsalphbet \(\Gamma\), dass aus unserem \(\Sigma\) und einem Blank \(\{B\}\) besteht.

Die oben definierte Eingabecodierung \(EC\)

Die oben definierte Ausgabecodierung \(AC\)

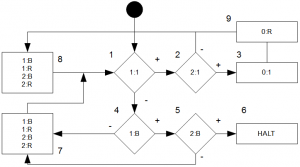
Und unserem Flussdiagramm \(F\):

Download: JFLAP-Datei Turing-Maschine 111.

Sieht etwas kompliziert aus, ist es aber nicht. Sicherlich könnte man das alles auch etwas einfacher gestalten.

Was tut die Maschine? Es zählt die Einsen, die auf den Bändern \(1\) und \(2\) auf gleicher Position stehen und schreibt dann eine \(1\) auf Band \(0\). Bei jedem Schritt werden die Zeichen auf Band \(1\) und \(2\) jedoch auch entfernt.

Würden wir die Maschine also mit \(0100101\) und \(0000100\) starten, so hätten wir am Ende die Ausgabe \(1\) auf Ausgabeband \(0\). Würden wir als Eingabe aber \(0100101\) und \(1010010\) wählen, so wäre das Ausgabeband leer.

Formal ausgedrückt bedeutet es

\((1,(\epsilon,B,\epsilon),(B,0100101,B),(B,000100,B))\) \(\vdash^*(6,(1,B,\epsilon),(\epsilon,B,\epsilon),(\epsilon,B,\epsilon))\)

Ihr kennt die \(\vdash^{*}\)-Notation ja bereits, aber dennoch zur Auffrischung: es bedeutet, dass ausgehend vom Marker \(1\) mit einem leeren Ausgabeband und \(0100101\) auf Band \(1\), sowie \(0000100\) auf Band \(2\), wir am Ende in Marker \(6\) (unsere \(HALT\)-Marke) landen und dabei folgende Bandbelegung haben: auf Band \(0\) steht eine \(1\), Band \(1\) und \(2\) sind leer.

Und so sieht der 2. Fall (\(0100101\) und \(1010010\)) aus:

\((1,(\epsilon,B,\epsilon),(B,0100101,B),(B,1010010,B))\) \(\vdash^*(6,(\epsilon,B,\epsilon),(\epsilon,B,\epsilon),(\epsilon,B,\epsilon))\)

Es befand sich keine \(1\) auf der gleichen Position auf beiden Bändern, so ist Band \(0\) am Ende der Berechnung ebenfalls leer.

Fertig!

Antwort zum Lernziel: das Flussdiagramm einer Turingmaschine besteht aus vier verschiedenen Befehlen (gehe links/rechts, schreibe Zeichen \(a\), prüfe ob Zeichen \(a\) auf dem Band steht), die auf den Bändern ausgeführt werden können. Die initiale Belegung belegt immer nur Band \(1-k\), wobei das Ausgabeband \(0\) leer bleibt und erst während der Berechnung beschrieben wird (oder eben nicht).

Die Worte, die auf den Bändern stehen können, sind über dem Alphabet \(\Sigma\) gebildet. Zusätzlich zu den Zeichen aus \(\Sigma\) wird auch noch das Blank-Zeichen \(B\) im Arbeitsalphabet \(\Gamma\) auf den Bändern verwendet.

Lernziel 2

Nachweis der Berechenbarkeit einfacher Wortfunktionen

Auch ist in diesem Beitrag bereits beschrieben, wie man das nachweisen kann. Das Verfahren ist ähnlich dem Beispiel für die Einzelschrittfunktion und dem Beweis der Addition mit einer Registermaschine, wo man Behauptungen aufstellt und diese durch vollständige Induktion beweist.

Formal ausgedrückt müssen wir zeigen, dass eine Wortfunktion dann berechenbar ist wenn es eine Turingmaschine gibt, die sie berechnet.

Eine Wortfunktion \(f:\subseteq(\Sigma^*)^k\rightarrow\Sigma^*\) heißt berechenbar, gdw. es eine Turingmaschine \(M\) gibt mit \(f=f_M\).

Beispiel: \(f(x)=1^{\#1(x)}\)

Wir haben als Ausgabe der Wortfunktion einfach nur die Anzahl der Einsen aus dem Wort \(x\).

Um zu beweisen, dass die berechenbar ist, müssen wir also eine Turingmaschine angeben, die den gleichen Ausgabewert hat wie unsere Funktion, so dass am Ende eben gilt: \(f=f_M\).

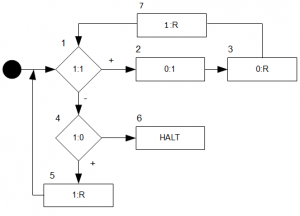
Das ist unser Flussdiagramm für diese äußerst komplizierte Konstruktion:

Und nun stellen wir uns die Frage, was wir beweisen wollen:

Behauptung: Für alle \(x\in\Sigma^{*}\) gilt

\((1,(\epsilon,B,\epsilon),(\epsilon,B,x))\vdash^*(6,(1^{\#1(x)},B,\epsilon),(x,B,\epsilon),(\epsilon,B,\epsilon),…)\)

Wir landen also beider Eingabe von \(x\) nach endlich vielen Schritten in Marker \(6\) und haben auf dem Ausgabeband die Anzahl der Einsen von \(x\), während auf Band \(1\) links vom Kopf unsere Eingabe steht, die wir gelesen haben.

Beweis

\(n=lg(x)\), d.h. wir zeigen die Korrektheit über die Länge unserer Eingabe \(x\).

\(n=0\): dabei ist die Eingabe leer, d.h. \(x=\epsilon\) und wir landen direkt in \((6,(\epsilon,B,\epsilon),(\epsilon,B,\epsilon),(\epsilon,B,\epsilon),…)\)

\(n\rightarrow n+1\): nun nehmen wir an, dass wir für alle Worte der Länge \(n\) über \(\Sigma\), d.h. für alle \(x\in W_n(\Sigma)\) die obige Behauptung gezeigt haben.

Jetzt können wir einen Schritt weiter gehen und \(x\in{W_{n+1}}(\Sigma)\) setzen. Dann gibt es ein \(x^{‚}\in{W_{n}}(\Sigma)\) und ein \(a\) aus \(\Sigma\) mit \(x=x^{‚}a\) mit

\((1,(\epsilon,B,\epsilon),(\epsilon,B,x^{‚}a))\vdash^*(6,(1^{\#1(x^{‚}a)},B,\epsilon),(x^{‚}a,B,\epsilon),(\epsilon,B,\epsilon),…)\)

wenn \(a=1\) und

\((1,(\epsilon,B,\epsilon),(\epsilon,B,x^{‚}a))\vdash^*(6,(1^{\#1(x^{‚})},B,\epsilon),(x^{‚}a,B,\epsilon),(\epsilon,B,\epsilon),…)\)

wenn \(a=0\).

Damit gilt die Behauptung für alle \(x\in{W_{n+1}}(\Sigma)\). Und wir haben \(f=f_M\) bewiesen.

Warum ist das so?

Es sieht zwar etwas kompliziert aus, ist es aber nicht wirklich. Schauen wir uns den ersten Fall doch mal genauer an:

Erklärung:

Wir haben ein \(x\in{W_{n}}(\Sigma)\), d.h. unser \(x\) mit der Länge \(n\) endet entweder mit einer \(1\) oder einer \(0\). Mehr Möglichkeiten haben wir nicht, denn das sind die einzigen Zeichen in unserem Alphabet \(\Sigma\).

Nehmen wir unser \(x\in{W_{n+1}}(\Sigma)\), d.h. es ist um ein Zeichen länger, ändert sich an der Anzahl der Möglichkeiten etwas? Nein, unser „\(+1\)“ endet immer noch entweder mit einer \(1\) oder einer \(0\).

Jetzt kommt unsere Fallunterscheidung ins Spiel mit einem Zeichen aus \(a\in\Sigma\), dass nur \(1\) oder \(0\) sein kann. Damit ist in jedem Fall \(x=x^{‚}a\), denn \(lg(x)=n+1\) und \(lg(x^{‚}a)=n+1\).

Wie sieht denn unsere Ausgabe am Ende aus wenn wir \(a=1\) haben? Auf dem Ausgabeband steht dann die Anzahl der Einsen von \(x^{‚}\) und \(a\), also \(1^{\#1(x^{‚}a)}\). Und bei \(a=0\)? Genau! Nur die Anzahl der Einsen von \(x^{‚}\), genau \(1^{\#1(x^{‚})}\).

Wenn wir es nun genau nehmen, gilt \(f=f_M\) noch nicht, denn

\(f(10111)=1111\), während

\(f_M=(6,(1111,B,\epsilon),(10111,B,\epsilon),(\epsilon,B,\epsilon),…)\)

Was tun? Hier hilft unsere Ausgabecodierung \(AC\) (Definition siehe oben), denn \(AC((6,(1111,B,\epsilon),(10111,B,\epsilon),(\epsilon,B,\epsilon),…))=1111\).

Jetzt erst gilt \(f=f_M\)!

Antwort zum Lernziel: um eine Wortfunktion als berechenbar nachzuweisen, müssen wir eine Turingmaschine angeben, die sie berechnet. Der formale Nachweis wird mittels vollständiger Induktion erbracht, indem man zeigt, dass für alle Eingaben  das passende Ergebnis am Ende der Berechnung (unser geliebtes Zeichen \(\vdash^*\)) auf dem Ausgabeband steht.

Lernziel 3

Erläuterung der Definition einer Bandmaschine

Hier hatten wir auch bereits in diesem Beitrag Vorarbeit geleistet. Der Unterschied zu Turingmaschinen mit \(k\) Arbeitsbändern ist nicht groß. Wir passen die Ein- und Ausgabecodierung an und ändern die Befehle so ab, dass sie nur auf Band \(0\) arbeiten.

Aus der Eingabecodierung für Mehrbandmaschinen mit

• \(EC^{(k)}(x_1,…,x_k):=((\epsilon,B,\epsilon),(\epsilon,B,x_1),…,(\epsilon,B,x_k),(\epsilon,B,\epsilon))\)

wird ganz einfach

• \(EC^{(k)}(x_1,…,x_k):=(\epsilon,B,x_1B…B,x_k)\).

Und nun zu den Befehlen:

• \(i:L\rightarrow L\)
• \(i:R\rightarrow R\)
• \(i:a\rightarrow a\)
• \(i:a?\rightarrow a?\)

Antwort zum Lernziel: die Befehle einer Turingmaschine (Mehrband) behalten auch bei Bandmachinen (Einband) ihre Gültigkeit. Nur arbeiten diese statt auf \(k+1\) (Ausgabeband + \(k\) Arbeitsbänder) Bändern nun auf einem einzigen Band \(0\).

Ebenso verhält es sich mit der Eingabecodierung, die angepasst werden muss. Für die Ausgabecodierung ändert sich nichts, es bleibt auf Band \(0\) als das längste Wort links vom Lesekopf.

Lernziel 4

Erläuterung der Grundidee des Beweises Turing-berechenbar = Band-berechenbar

Das ist Turings ursprüngliche Konstruktion.

Wenn wir doch schon so schön mit Mehrbandmaschinen arbeiten könne, wozu dann Einband? Weil beide Maschinen von der Berechnungsstärke äquivalent sind und letztere weniger kompliziert sind. Persönlich finde ich, dass man mit den Mehrbandmaschinen einfacher hantieren kann, aber sei es drum.

Die Grundidee des Beweises habe ich bereits hier beschrieben, so dass wir uns nur noch um das Lernziel kümmern müssen. Formal ausgedrückt lässt sich festhalten:

Zu jeder Einbandmaschine \(M\) gibt es eine Mehrbandmaschine \(M^{‚}\) mit dem gleichen Bandalphabet wie \(M\), so dass gilt: \(f_M=f_{M^{‚}}\).

Zu jeder Mehrbandmaschine \(M^{‚}\) gibt es eine Einbandmaschine \(M\), so dass gilt: \(f_M=f_{M^{‚}}\).

Damit haben wir uns auch schon enttarnt: wir können die Mehrbandmaschine durch ein vergrößertes Bandaphabet simulieren. Anders herum bleibt das Bandalphabet natürlich gleich, denn es ist ja bereits groß.

Antwort zum Lernziel: die Simulation der Mehrband- in einer Einbandmaschine erfolgt auf Basis eines vergrößerten Alphabets für die Darstellung der Position der Leseköpfe auf den simulierten Bändern.

Damit erhalten wir „Spuren“ auf dem einen Band für die eig. Eingabe und zusätzliche Spuren für die Position der Leseköpfe um die getrennt beweglichen Leseköpfe auf den vormals \(k\) Spuren zu simulieren.

Diese neuen Symbole, die wir für die Markierung der Leseköpfe brauchen werden Hilfssymbole genannt und bereichern unser Arbeitsalphabet \(\Gamma\) wenn wir sie nicht durch eine Codierung eliminiert haben (siehe nächstes Lernziel).

Lernziel 5

Erläuterung der Grundidee des Beweises, dass man bei Bandmaschinen ohne Hilfssymbole auskommt

Auch hier ist im alten Beitrag die Grundidee bereits beschrieben worden. Ich fasse mich daher sehr schmallippig.

Antwort zum Lernziel: die neuen Hilfssymbole für die simulierte Kopfpositionen der Bänder einer Mehrbandmaschine werden anstatt durch Aufblähen des Arbeitsalphabets mit neuen Zeichen einfach durch eine erweiterte Länge der Wörter über dem alten Arbeitsalphabet \(\Gamma\) codiert.

Dadurch ist es möglich, dass das Bandalphabet einer Einbandmaschine bei \(\Gamma=\Sigma\cup\{B\}\) bleibt.

Diesen Beitrag habe ich etwas zügig getippt, es könnten sich also ein paar Fehler eingeschlichen haben. Wer etwas sieht: ab damit in die Kommentare. Danke!

In dieser Kurseinheit gibt es zwar nicht viele Lernziele, aber lasst euch nicht täuschen: sie sind wichtig. Die Beiträge zu diesem Thema, die ich auch im passenden Kontext in diesem Beitrag verlinkt habe sind:

• Primitive Rekursion/LOOP Berechenbarkeit
• Mue-Rekursion und WHILE/LOOP-Berechenbarkeit
• Cantorsche Tupelfunktion

Starten wir aber einfach wieder anhand der Lernziele und kämpfen uns da durch.

Lernziel 1

Angabe und Erläuterung der Definition und der Eigenschaften der Cantorschen Tupelfunktion

Zum Glück habe ich bereits hier einen langen Beitrag zum Thema erstellt und wiederhole mich deswegen nicht, sondern springe sofort zur Antwort.

Antwort zum Lernziel: mit der Cantorschen Tupelfunktion ist es uns möglich einem \(n\)-Tupel mit Elementen aus \(\mathbb{N}\) eine einzige, eindeutige Zahl aus \(\mathbb{N}\) zuzuordnen (Reduktion). Durch diese bijektive Abbildung von \(\mathbb{N}^n\rightarrow\mathbb{N}\) können wir uns auf die Berechnung von einstelligen Funktionen beschränken.

Einen weiteren prominenten Platz hat die Cantorsche Tupelfunktion bei dem Vergleich von Mengen: zwei Mengen sind gleichmächtig wenn man zwischen ihnen eine Bijektion herstellen kann.

Lernziel 2

Erläuterung der Abschlusseigenschaften berechenbarer Zahlenfunktionen

Ich bin mir hier gerade etwas unschlüssig: im Skript ist nicht mehr viel zu dem Thema drin, als der Satz zur Substitution, primitive Rekursion, \(\tilde{\mu}\) und der Umkehrfunktion. Vielleicht dann am besten an ein paar Beispielen?

Substitution

Zunächst haben wir zwei ggf. partielle Funktionen \(g:\subseteq\mathbb{N}^m\rightarrow\mathbb{N}\) und ggf. partielle Funktionen \(h_1\) bis \(h_m\) (d.h. so viele Funktionen wie der Definitionsbereich von \(g\) Parameter hat), mit \(h_1,…,h_m\subseteq\mathbb{N}^k\rightarrow\mathbb{N}\). Alle Funktionen sind berechenbar. Dann ist auch die Substitution \(Sub(g,h_1,…,h_m)\) berechenbar.

\(Sub(g,h_1,…,h_m)\subseteq\mathbb{N}^k\rightarrow\mathbb{N}\) ist definiert durch \(Sub(g,h_1,…,h_m)(x):=g(h_1(x),…,h_m(x))\)

Viel Zeug, oder? Keine Sorge, ist ganz easy.

Beispiel

\(g(x,y)=x+y\)

\(h_1(x,y,z)=x+y\)

\(h_2(x,y,z)=x+z\)

Die Substitution sieht nun so aus:

\(Sub(g,h_1,h_2)(x,y,z)=g(h_1(x,y,z),h_2(x,y,z))\).

Belegen wir unsere Funktion mit Werten: \(x=2,y=3,z=4\)

\(\begin{array} Sub(g,h_1,h_2)(2,3,4)&=g(h_1(2,3,4),h_2(2,3,4))\\&=g(5,h_2(2,3,4))\\&=g(5,6)\\&=11\end{array}\)

War doch trivial, oder (das wollte ich immer schon mal sagen!)?

Primitive Rekursion

Das ist ein klein wenig ekeliger als die Substitution, aber wir bekommen das gleich noch klein.

Auch hier haben wir zwei Funktionen  \(g:\mathbb{N}^k\rightarrow\mathbb{N}\) und  \(h:\mathbb{N}^{k+2}\rightarrow\mathbb{N}\), die berechenbar sind (Achtung: sie müssen auch total sein, denn sonst können wir nicht über diese „rekursivieren“). Wenn das der Fall ist, dann ist auch \(Prk(g,h)\) berechenbar.

\(Prk(g,h)\) ist definiert als:

\(f(x,0) = g(x)\)

\(f(x,y+1)=h(x,y,f(x,y))\)

Für alle \(x\in\mathbb{N}^k\) und \(y\in\mathbb{N}\). Man sieht bereits jetzt, dass wir rekursiv arbeiten. Noch deutlicher wird es an einem Beispiel.

Beispiel

\(g(x,z)=x+z\)

\(h(a,b,x,z)=a+b+x+z\)

Nehmen wir einfach mal \(y=3\) (\(3\)-malige Rekursion) und \(x=2,z=3,a=4,b=5\).

\(\begin{array} Prk(g,h)(2,3)&=f(2,3,3)\\&=h(2,3,2,f(2,3,2))\\&=h(2,3,2,(h(2,3,1,f(2,3,1))))\\&=h(2,3,2,(h(2,3,1,(h(2,3,0,f(2,3,0))))))\\&=h(2,3,2,(h(2,3,1,(h(2,3,0,g(2,3))))))\\&=h(2,3,2,(h(2,3,1,(h(2,3,0,5)))))\\&=h(2,3,2,(h(2,3,1,10)))\\&=h(2,3,2,16)\\&=23\end{array}\)

Versuchen wir das mit \(y=2\):

\(\begin{array} Prk(g,h)(2,2)&=f(2,3,2)\\&=h(2,3,1,f(2,3,1))\\&=h(2,3,1,(h(2,3,0,f(2,3,0))))\\&=h(2,3,1,(h(2,3,0,5)))\\&=h(2,3,1,10)\\&=16\end{array}\)

Viel Text, aber sicherlich gut nachzuvollziehen. Wir loopen und also durch die Funktionen mit einer festen Anzahl an Schleifen! In diesem Beitrag habe ich die primitive Rekursion etwas detaillierter betrachtet.

Und was ist wenn wir keine feste Anzahl an Schleifen haben können? Dann hilft uns unser \(\mu\)-Operator.

\(\tilde{\mu}\)

Ist \(h\) mit \(h:\subseteq\mathbb{N}^{k+1}\rightarrow\mathbb{N}\) berechenbar, so ist es auch \(\tilde{\mu}(h)\). Wie ihr seht, auch hier ist \(h\) total. Was ist \(\tilde{\mu}\)?! \(\tilde{\mu}:\subseteq\mathbb{N}^{k}\rightarrow\mathbb{N}\). Es ist definiert durch:

\(\tilde{\mu}(h)(x)=\mu y[h(x,y)=0]\)

What the… Entspannung, Entspannung! Das ist nichts weiter als unsere \(\mu\)-Rekursion. Ich suche gerade im Skript ob wir das bereits irgendwo auf den vorherigen Seiten hatten… witzig. Hatten wir nicht. Das ist wirklich die erste Erwähnung. Und dann gleich ins kalte Wasser. Nicht schlimm, denn unser \(\tilde{\mu}\) ist nichts weiter, als der Operator, der es uns erlaubt auch Dinge zu berechnen, wo wir die genaue Anzahl an Schleifendurchläufen noch nicht wissen.

Und zwar indem wir unserer zu berechnende Funktion so weit umformen, dass wir beim Ende der Berechnung auf eine Nullstelle stoßen. Ich werde das nicht groß ausführen, sondern verweise ganz frech auf meinen alten Beitrag zum Thema.

Umkehrfunktion \(f^{-1}\)

Das schwerste zum Schluss. Hier gehen wir davon aus, dass \(f\) injektiv ist (wichtig!). Wir beschränken uns auch auf einstellige Funktionen. Warum? Na? Na? Genau: aufgrund der Cantorschen Tupelfunktion können wir das. Wenn diese Funktion also berechenbar ist, so ist es auch ihre Umkehrfunktion. Klingt logisch. Ist es auch.

Während für \(f\) Totalität und Injektivität gefordert ist, können wir bei \(f^{-1}\) bei einer ggf. partiellen Funktion rauskommen. Das liegt daran, dass wir in der Bildmenge von \(f\) evtl. Elemente haben, die wir mit unserer Funktion nicht „treffen“. Diese landen aber für \(f^{-1}\) dennoch in der Definitionmenge, sind aber nicht definiert. Damit ist \(f^{-1}\) eben partiell.

Beispiel

\(f(x) = x+5\) mit der Umkehrfunktion \(f^{-1}(\tilde{x})=\tilde{x}-5\). Setzen wir \(x=10\) und \(\tilde{x}=f(x)\), so haben wir:

\(f(10)=15\)

\(f^{-1}(15)=10\)

Passt.

Damit haben wir die Abschlusseigenschaften für berechenbare Zahlenfunktionen durch.

Antwort zum Lernziel: Funktionen, die sich aus den Funktionen Substitution, primitive Rekursion, \(\mu\)-Rekursion und der inversen Funktion zusammensetzen sind ebenfalls berechenbar.

Für die Substitution können die Funktionen auch partiell sein, für de primitive und \(\mu\)-Rekursion sind wir jedoch auf totale Funktionen angewiesen, da wir sonst nicht durch die Schleifendurchläufe kommen. Während wir bei der primitiven Rekursion zwingend die Anzahl der Schleifendurchläufe kennen müssen, ist es uns bei der \(\mu\)-Rekursion durch das „Nullsetzen“ der Funktion nicht wichtig. Es bricht eben ab wenn die Nullstelle gefunden ist. Wie lange es dauert wissen wir nicht.

Ersteres ist das Äquivalent zur \(LOOP\)-Schleife („tue etwas genau \(x\) Mal“), während die \(\mu\)-rekursion einer \(WHILE\)-Schleife („tue etwas bis…“) entspricht.

Für die inverse Funktion benötigen wir neben einer totalen Funktion \(f\) jedoch auch die Eigenschaft der Injektivität für \(f\), da wir nur auf maximal ein Element aus der Bildmenge abbilden dürfen, da sonst die Umkehrabbildung auf zwei unterschiedliche Elemente abbilden würde.

Lernziel 3

Definition der WHILE-Programme, Erläuterung ihrer Semantik und Angabe des Zusammenhangs zu berechenbaren Funktionen

Letztes Lernziel in dieser Kurseinheit. In diesem Beitrag sind die Details bereits herausgearbeitet, ich kümmere mich daher nur um die Definition und Semantik aus dem Skript. Das Fazit kann man wortwörtlich eig. auch für die Antwort zum Lernziel übernehmen. Also kümmern wir uns um die Syntax und die Semantik.

\(R_i+\) und \(R_i-\) sind \(WHILE\)-Programme

Dabei addiert \(R_i+\) im \(i\)-ten Registereine \(1\), \(R_i-\) subtrahiert eine \(1\) im \(i\)-ten Register.

IF \(R_i=0\) THEN \(P\) ELSE \(Q\)

Wir gehen davon aus, dass \(P\) und \(Q\) selbst \(WHILE\)-Programme sind.

WHILE \(R_i\neq 0\) DO \(P\)

Kennen wir auch schon. Solange das Register \(R_i\) nicht \(0\) ist, wird \(P\) ausgeführt.

Zusätzlich dazu haben wir noch unser kleines Tau \(\tau\). Dadurch weisen wir unseren oben beschriebenen Kommandos tatsächliche Funktionen auf der Datenmenge \(D=\mathbb{N}^{\mathbb{N}}\) zu, die wir bereits verbal beschrieben haben (sie ist die uns bekannte Datenmenge der Registermaschinen). Als Beispiel nehmen wir \(R_i+\) und \(R_i-\):

\(\tau(R_i+)(a_0,a_1,…):=(a_0,a_1,…,a_i+1,…,)\)

\(\tau(R_i-)(a_0,a_1,…):=(a_0,a_1,…,a_i-1,…,)\)

Wir können einem kompletten \(WHILE\)-Programm mittels \(\tau\) ebenfalls eine Ausgabe auf der Datenmenge \(D\) beschaffen: \(\tau(P)\). Und damit haben wir dann die komplette Registerausgabe unserer Maschine, die das Programm \(P\) berechnet. Damit schaffen wir es, dass unser Programm auf der Eingabecodierung einer Registermaschine operieren kann und uns auch eine Ausgabecodierung der Registermaschine liefert (siehe vorheriger Beitrag).

Noch eine kleine Definition für die \(WHILE\)-Berechenbarkeit

Wir nennen eine Funktion \(f:\mathbb{N}^k\rightarrow\mathbb{N}\) \(WHILE\)-berechenbar genau dann wenn gilt: \(f=AC(\tau(P)(EC))\)

Ähnliches Spiel wie im Beitrag zu KE1. Wir haben unterschiedliche Datenmengen für \(\tau\) und für die Flussdiagramme der Registermaschinen. Mit \(EC\) und \(AC\) wandelt wir diese nur ineinander um.

Das führt uns direkt zum Zusammenhang zu den berechenbaren Funktionen.

Beispiel

Funktion \(f(x,y)=x+y\) (operiert auf \(\mathbb{N}^2\rightarrow\mathbb{N}\))

Dazu haben wir ein \(WHILE\)-Programm \(P\), welches uns die Funktion \(f\) berechnet. Es operiert auf \(\mathbb{N}^3\rightarrow\mathbb{N}^3\)

R0=R1;

WHILE R2 NOT 0 DO

  R0+;

  R2-;

END;

Wir können auch ein Flussdiagramm \(F\) einer Registermaschine \(M\) angeben, dass uns die gleiche Funktion raushaut.

Während das Flussdiagramm ebenfalls auf \(\mathbb{N}^3\rightarrow\mathbb{N}^3\) operiert, haben wir bei der Registermaschine jedoch \(\mathbb{N}^3\rightarrow\mathbb{N}\).

Damit gilt \(f=\tau(P)=f_M=f_F\). Oder doch nicht? Spielen wir das doch einfach mal mit \(x=2,y=3\) durch:

\(f(2,3)=5\)

\(\tau(P)(0,2,3)=(5,2,0)\)

\(f_M(0,2,3)=5\)

\(f_F(0,2,3)=(5,2,0)\)

Okay, die Berechnung ist anscheinend in Ordnung. Aber die Ausgabe von z.B. \(\tau(P)(0,2,3)=(5,2,0)\) ist sicher nicht gleich \(f_M(0,2,3)=5\) (siehe die Definition der Eingabe- und Ausgabecodierung von Registermaschinen im Lernziel 4 von Beitrag zu KE1).

Hier kommen unsere Funktionen \(EC\) und \(AC\) bei allen drei Berechnungsarten ins Spiel, die unsere Eingabe und unsere Ausgabe entsprechend umformen, so dass sie passen.

Definieren wir also z.B. \(AC\) für \(\tau(P)\) neu: \(AC(x,y,z)=x\), so haben wir

\(\begin{array}{}AC(\tau(P)(0,2,3))&=AC(5,2,0)\\&=5\end{array}\)

Damit würde \(f_M=AC(\tau(P))\) wieder passen.

Das spannende also daran ist, dass es durchaus vorkommen kann, dass unser Flussdiagramm, unsere Registermaschine oder unser \(WHILE\)-Programm nicht alle auf einer Datenmenge operieren, sondern alle auf unterschiedlichen Mengen (warum auch immer). Um aber zu sagen, dass z.B. \(\tau(P)=f_M\) gilt, müssen wir sie evtl. umgestalten. Für \(\tau(P)=f_F\) brauchen wir das hingegen – wie wir oben gesehen haben – nicht.

Lange Rede, kurzer Sinn:

Zu jedem \(WHILE\)-Programm gibt es ein Flussdiagramm einer Registermaschine mit \(\tau(P)=f_F\)

Zu jedem Flussdiagramm einer Registermaschine gibt es ein \(WHILE\)-Programm mit \(f_F=\tau(P)\) mit einer \(WHILE\)-Schleife.

Damit gilt: die Funktion \(f\) ist \(WHILE\)-berechenbar genau dann wenn sie Register-berechenbar ist.

Antwort zum Lernziel: die \(WHILE\)-Programme bestehen aus bedingten Anweisungen (\(IF\)) und Schleifen (\(WHILE\)), sowie Anweisungen zum Register hoch- oder runterzählen und Hintereinanderausführungen von Anweisungen.

Der Zusammenhang zu berechenbaren Funktionen kommt daher, dass man zu jedem \(WHILE\)-Programm eine Registermaschine angeben kann, die die selbe Funktion berechnet und zu jeder Registermaschine ein \(WHILE\)-Programm existiert.

\(WHILE\)-Programme sind mächtiger als \(LOOP\)-Programme: man kann \(LOOP\)-Schleifen mit \(WHILE\)-Schleifen nachbilden, aber nicht anders herum, da man die Anzahl der Schleifendurchläufe im Vorfeld nicht bei jeder \(WHILE\)-Schleife kennt.

Die \(LOOP\)-Anwendungen sind das Äquivalent zur primitiven Rekursion, während die \(WHILE\)-Programme erst mit dem \(\mu\)-Operator (durch „Nullsetzen“ der Funktion) nachgebildet werden können.