TIA: Flussdiagramme, Maschinen und berechenbare Zahlenfunktionen (Lernziele KE1, Update 2)

Update: Einwand von Felix aufgenommen.

Update: Marion hat einen Fehler bei der Berechnung der $ES$ gefunden. Danke!

Update: Eine Registermaschine kann nicht die Subtraktion, sondern nur die arithmetische Differenz.

Update: Hinweis darauf, dass das erste Register bei der Eingabecodierung $EC$ für eine Maschine belegt werden kann (wir haben keine Einschränkungen), aber nicht durch die Eingabecodierung für eine Registermaschine!

Als ich die ersten Beiträge zur Kurseinheit 1 von Teil A der theoretischen Informatik geschrieben habe, orientierte ich mich an den Themen. Entstanden sind damit die Unterbeiträge:

• Normale und allgemeine Registermaschinen
• Einzelschritt- und Schrittzahlfunktion sowie Übergangsrelationen (Update)
• Beweis der Addition zweier Register mit einer Registermaschine

Irgendwann, gegen Ende der Kurseinheit 5 habe ich gemerkt, dass es vielleicht sinniger ist anhand der Lernziele zu gehen. Das bringt etwas mehr Struktur in die Beiträge und wirft einen roten Faden durch das Skript.

Als ich dann bei Kurseinheit 7 von Teil B angelangt war, hat sich mein Entschluss gefestigt die alten Beiträge ebenfalls zu überarbeiten. Was ich hiermit also tun möchte.

Lernziel 1

Angabe und Erläuterung der Definition des Flussdiagramms

Ich würde vorschlagen, wir definieren wieder und erklären die Definition Zeile für Zeile: das Flussdiagramm ist ein 4-Tupel $F=(Q,D,\sigma,q_o)$

$Q$: Markenmenge

$D$: Datenmenge

$q_0$: Startmarke

$\sigma$: zu jeder Marke gehört entweder eine Zuweisung $(f,p)$ oder eine Verzweigung/Test $(S,p,p^{'})$

Beispiel gefällig?

Beispiel: $F_1=(Q,D,\sigma,q_0)$ mit

$Q=\{1,2,3,4\}$: wir haben nur vier Marken im Flussdiagramm

$D=\mathbb{N}^2$: wir operieren auf max. zweistelligen, natürlichen Zahlen

$q_0=1$: die Anfangsmarke ist $1$

Und nun kommt unsere Funktion, die jeder Marke eine Operation zuweist. Das macht das Flussdiagramm nämlich erst aus.

$\sigma(1)=(y=1,2)$ (Zuweisung)

$\sigma(2)=(y>x,4,3)$ (Verzweigung/Test)

$\sigma(3)=(y=y+1,2)$ (Zuweisung)

$\sigma(4)=HALT$ (Haltemarke)

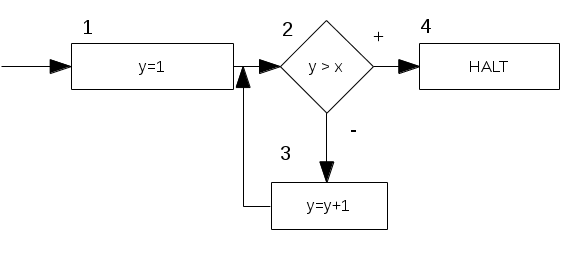
Und wenn wir $F_1$ auf Papier bringen:

Nicht so schwer, oder? Was tut das Flussdiagramm $F_1$? Nichts besonderes: es zählt nur $y$ hoch bis es größer ist als $x$. Nicht besonders sinnvoll, aber kurz (ich bin faul, sorry) und anschaulich.

Antwort zum Lernziel: Ein Flussdiagramm besteht aus einer Marken- und Datenmenge, einer Startmarke und einer Funktion, die jeder Marke aus der Markenmenge eine Zuweisung oder eine Verzweigung zuordnet.

Lernziel 2

Angabe und Erläuterung der Semantik des Flussdiagramms

Semantik? Bedeutung! Das Flussdiagramm $F$ definiert nämlich nichts anderes als eine Funktion $f_F$, die aus den Parametern (oben waren es $x$ und $y$) in einer Endkonfiguration (so denn es eine gibt) ein Ergebnis generiert. Die Semantik eines Flussdiagramms gliedert sich in folgende Begriffe:

• Konfiguration: z.B. Anfangs- und Endkonfiguration sowie Zwischenkonfigurationen
• Einzelschrittfunktion: Übergang in einem Berechnungsschritt von einer Konfiguration in eine andere
• Schrittzahlfunktion: $div$ wenn es zu einer Eingabe keine Endkonfiguration gibt oder die Anzahl der Schritte, die zu einer Eingabe bis zur Endkonfiguration geführt haben
• Gesamtschrittfunktion: Endkonfiguration zu einer Eingabe. Wenn sie existiert. Ansonsten $div$.
• Semantik: Das Ergebnis

Beispiel: $F_1=(Q,D,\sigma,q_0)$ (von oben)

Sagen wir, wir starten $F_1$ mit $x=2$ und $y=0$.

• Anfangskonfiguration: $(1,(2,0))$ und Endkonfiguration: $(4,(2,3))$ (Zwischenkonfigurationen lasse ich mal weg)
• Einzelschrittfunktion: z.B. $ES(1,(2,0)=(2,(2,1))$. Nach einem Schritt befinden wir uns in Marke $2$ und haben nur $y=1$ gesetzt. Würden wir aber z.B. $ES^6(1,(2,0))$ nehmen, so müssten wir fünf Berechnungsschritte im Flussdiagramm ausführen und wären bei

$\begin{align}ES^6(1,(2,0))&=ES^5(2,(2,1))\\&=ES^4(3,(2,1))\\&=ES^3(2,(2,2))\\&=ES^2(3,(2,2))\\&=ES(2,(2,3))\\&=(4,(2,3))\end{align}$

(Update: Nach Einwand von Felix korrigiert. Danke!)

• Schrittzahlfunktion: $SZ(1,(2,0))=7$. Nach $7$ Schritten kommen wir, ausgehend von der Anfangskonfiguration $(1,(2,0))$ in die Endkonfiguration $(4,(2,3))$.
• Gesamtschrittfunktion: $GS(1,(2,0))=(4,(2,3))$. Die Endkonfiguration zur Anfangskonfiguration $(1,(2,0))$ ist eben $(4,(2,3))$ und damit unsere Gesamtschrittfunktion.
• Semantik: $f_{F_1}(2,0)=(2,3)$. Das Ergebnis der harten Arbeit unseres Flussdiagrsmms.

Auch nicht viel schwerer als Lernziel 1.

In einem alten Beitrag habe ich das bereits für Registermaschinen aufgegriffen.

Antwort zum Lernziel: das Flussdiagramm definiert eine Funktion $f_F$ (die Semantik des Flussdiagramms) auf der Datenmenge des Flussdiagramms, welche von einer Anfangskonfiguration (Startmarke, Eingabe) nach endlich vielen Schritten zu einer Endkonfiguration (Endmarke, Ausgabe) führt. Oder auch nicht.

Die Belegung der Variablen im Flussdiagramm ist das Ergebnis der Berechnung, es gilt dann $f_F(Eingabe)=Ausgabe$. Gibt es zu der Eingabe kein Ergebnis, so ist $f_F(Eingabe)=div$.

Lernziel 3

Angabe und Erläuterung der Definition und Semantik einer Maschine

Kommen wir nun zu den Maschinen. Warum reicht uns das Flussdiagramm von oben nicht? Weil die Datenmenge $D$ des Flussdiagramms meistens nicht mit der Definitions- oder Bildmenge unserer durch das Flussdiagramm darzustellenden Funktion übereinstimmen wird. Wir brauchen hier also zusätzlich noch ein paar andere Dinge: eine Maschine ist ein 5-Tupel mit $M=(F,X,Y,EC,AC)$.

$F$ ist ein Flussdiagramm (siehe oben)

$X$ ist eine Eingabe- und $Y$ eine Ausgabemenge.

$EC:X\rightarrow D$: Eingabecodierung. Es ist nichts weiter als eine Funktion, die aus einem Element aus $X$ eine Eingabecodierung aus $D$ für unser Flussdagramm ausgibt. Under Flussdiagramm nimmt nämlich keine Elemente aus $X$, sondern nur aus $D$ entgegen.

$AC:D\rightarrow Y$: Ausgabecodierung. Ebenfalls nur eine Funktion, die hier jedoch zu einem Element aus $D$, der Datenmenge des Flussdiagramms ein Element aus der Ausgabemenge $Y$ zuweist.

Damit berechnet $M$, unsere Maschine also eine Funktion $f_M=AC(f_F(EC))$

Das letztere erschließt sich wahrscheinlich nicht sofort. Aber wie können das an einem Beispiel etwas anschaulicher gestalten.

Achtung (Update): während wir bei der Eingabecodierung bei einer Maschine es zulassen, dass wir das erste Register belegen, tun wir das keinesfalls bei einer Registermaschine! Das ist bei der Initialbelegung durch die Funktion $EC$ nicht zulässig, denn es fungiert als Ergebnisregister und ist initial immer mit $0$ belegt!

Beispiel: Maschine $M$ mit dem Flussdiagramm von oben, $x=2$ und den zusätzlichen Mengen und Funktionen

$X,Y=\mathbb{N}$: die Mengen unserer Eingabe- und Ausgabecodierungen für unsere Maschine sind nicht mehr Tupel ($\mathbb{N}^2$), wie sie das Flussdiagramm brauchst, sondern bestehen nur noch aus einem einzigen Element.

$EC:X\rightarrow D$ mit $EC(x)=(x,0)$.

$AC:D\rightarrow Y$ mit $AC(x,y)=y$

Wir können unsere Maschine $M$ also einfach nur mit $x$ füttern und erhalten durch die Eingabefunktion $EC$ auch unser $y$ für die Eingabe in unser Flussdiagramm. Ähnliches gilt für die Ausgabecodierung: unser Flussdiagramm gibt uns $(x,y)$ als Ausgabe heraus, was wir mit der Funktion $AC$ in $y$ umwandeln.

Setzen wir also $x=2$ mal ein:

$EC(x)=(2,0)$. Damit füttern wir unser Flussdiagramm und bekommen als Ausgabe des Flussdiagramms $f_F=(2,3)$. Das werfen wir in unsere Ausgabecodierung $AC(2,3)=3$ und haben die Ausgabe unserer Maschine $f_M$.

Der letzte Punkt unserer Maschine mit ausgefülltem $x=2$ bedeutet also:

$\begin{align}f_M&=AC(f_F(EC(2)))\\&=AC(f_F(2,0))\\&=AC(2,3)\\&=3\end{align}$

That's it.

Antwort zum Lernziel: eine Maschine tut für uns also nichts anderes, als es uns zu ermöglichen nicht mehr auf der Datenmenge $D$ des Flussdiagramms operieren zu müssen. Durch die "Eingabecodierungs-Funktion" $EC$ können wir aus einer beliebigen Eingabemenge $X$ in die Datenmenge $D$ des Flussdiagramms abbilden und so unser Flussdiagramm mit einer passenden Eingabe füttern.

Mittels der "Ausgabecodierungs-Funktion" $AC$ gelingt uns auch der Rückweg aus der Ausgabe des Flussdiagramms (die ja ein Element aus $D$ ist) in die Ausgabemenge $Y$.

Damit ist die Semantik einer Maschine die Funktion $f_M\subseteq X\rightarrow{Y}$, die mit Hilfe von $EC$ und $AC$ die Mengen $X$ und $Y$ von, bzw. in die Datenmenge $D$ für das Flussdiagramm überführt. Es gilt somit $f_M=AC(f_F(EC))$ wenn wir von einer Anfangskonfiguration zu einer Endkonfiguration kommen. Ansonsten ist $f_M=div$.

Lernziel 4

Angabe und Erläuterung der Definition einer Registermaschine

Kommen wir nun zu den Registermaschinen. Den eig. Stars dieser Kurseinheit. Ich hatte bereits in diesem Beitrag etwas zum Thema geschrieben. Es macht also keinen Sinn das hier noch einmal zu Wiederholen. Daher: bitte dort nachlesen und wiederkommen 😉

Update: nicht vergessen, die Eingabecodierung für eine Registermaschine belegt nicht das erste Register $R_0$!

$EC^{(k)}(x1,...,x_k):=(0,x_1,...,x_k)$

Ebenso ergeht es uns mit der Ausgabecodierung: uns ist egal, was in den anderen Registern steht, wir finden nur das erste Register spannend:

$AC(a_0,a_1,...):=a_0$

Antwort zum Lernziel: die Registermaschinen bestehen aus Registern mit durch die Eingabecodierung induzierten Registerbelegungen und der "Ausgabecodierungs-Funktion", welche uns das 1. Register (Register $R_0$) der Registermaschine als Ausgaberegister festlegt. Dadurch ist es uns nur möglich die Register $R_1-R_m$ mittels Eingabecodierung zu belegen.

Die Registermaschine verfügt nur über drei Grundoperationen: Addition von $1$, Subtraktion arithmetische Differenz und Test auf $0$.

Lernziel 5

Angabe und Erläuterung der Definition einer verallgemeinerten Registermaschine

Auch die Erläuterungen zur verallgemeinerte Registermaschine sind hier zu finden. Daher kümmern wir uns nur um das Lernziel.

Antwort zum Lernziel: Durch die verallgemeinerte Registermaschine ist es uns möglich weitaus mehr Operationen als die Grundoperationen Addition und Subtraktion von $1$, sowie Test auf $0$ durchzuführen.

Diese Operationen werden jedoch aus den Grundoperationen zusammengesetzt und erlauben es uns Registerinhalte miteinander zu vergleichen oder Registern Werte zuzuweisen, die durch Funktionen berechnet wurden (wobei Registerinhalte der Registermaschine selbst als Parameter dieser Funktion fungieren können).

Lernziel 6

Angabe der Definition einer berechenbaren Zahlenfunktion

Ich gebe mal ganz frech die Definition aus dem Skript wieder:

Eine Funktion $f:\subseteq\mathbb{N}^k\rightarrow\mathbb{N}$ heißt berechenbar wenn es eine $k$-stellige Registermaschine $M$ gibt, die sie berechnet, so dass gilt: $f=f_M$.

Das ist eine der zentralen Definitionen im Teil A der theoretischen Informatik und findet sich auch häufig als Frage in den Protokollen der mündlichen Prüfung wieder: diese Definition sagt uns, dass wir eine Funktion dann berechenbar nennen können, wenn wir eine Registermaschine angeben, die sie berechnet und im Endeffekt auf die Grundoperationen Addition und Subtraktion von $1$ sowie Test auf $0$ zurückführt.

Beispiel: $f(x,y)=x+y$

Wollen wir also nachweisen, dass die Funktion $f$ berechenbar ist, so müssen wir eine Registermaschine inkl. Flussdiagramm angeben, dass uns die gleiche Ausgabe in Register $R_0$ liefert, wie die Funktion $f$.

Für Details und den Beweis, dass die Addition zweier Register ($f(x,y)=x+y$) berechenbar ist, empfehle ich euch hier den alten Beitrag zum Thema.

Antwort zum Lernziel: Wir können eine Funktion mit $k$ Parametern also berechenbar nennen wenn wir sie mit einer $k$-stelligen Registermaschine und der Grundoperationen innerhalb eines Flussdiagramms berechnen können., so dass gilt: $f = f_M$.

Lernziel 7

Zeigen, dass eine Funktion berechenbar ist

Das Thema wurde ebenfalls hier detaillierter besprochen und gezeigt wie man eine Funktion (das angesprochene Beispiel mit der Addition zweier Register) als berechenbar nachweist. Ich begnüge mich also hier mit dem letzten Lernziel dieser Kurseinheit.

Antwort zum Lernziel: Um zu beweisen, dass eine Funktion berechenbar ist, muss man diese am Ende nur mit den Grundoperationen Subtraktion und Addition von $1$ und Test auf $0$ abbilden können.

Hat man z.B. die Addition mittels dieser Grundoperationen nachgebildet und mittels vollständiger Induktion bewiesen, dass sie für alle Werte das gewünschte Ergebnis liefert, so kann man diese komplexe Operation nun in seiner verallgemeinerten Registermaschine für weitere Beweise anderer Funktionen nutzen.

Z.B. kann man ausgehend von den Grundoperationen die Addition zweier Register $x+y$ beweisen und anschließend mit der Addition den Beweis der Multiplikation $x\cdot y$ angehen. Mit der Multiplikation gelingt uns dann das Beweisverfahren für die Exponentialfunktion $x^y$, usw.

Die Lernziele von Kurseinheit 1 haben wir damit durch. Noch 6 und der Kurs ist komplett 😉 Bei Fehler wie immer: ASAP in die Kommentare damit falsches Zeug nicht so lange online bleibt!

Datum: 17. Juni 2013
Kategorie: Theoretische Informatik
Kommentarfeed: RSS 2.0 • Trackback: Trackback-Url

Sie können zum Ende springen und ein Kommentar hinterlassen. Pingen ist im Augenblick nicht erlaubt.