In dieser Kurseinheit gibt es zwar nicht viele Lernziele, aber lasst euch nicht täuschen: sie sind wichtig. Die Beiträge zu diesem Thema, die ich auch im passenden Kontext in diesem Beitrag verlinkt habe sind:
- Primitive Rekursion/LOOP Berechenbarkeit
- Mue-Rekursion und WHILE/LOOP-Berechenbarkeit
- Cantorsche Tupelfunktion
Starten wir aber einfach wieder anhand der Lernziele und kämpfen uns da durch.
Lernziel 1
Angabe und Erläuterung der Definition und der Eigenschaften der Cantorschen Tupelfunktion
Zum Glück habe ich bereits hier einen langen Beitrag zum Thema erstellt und wiederhole mich deswegen nicht, sondern springe sofort zur Antwort.
Antwort zum Lernziel: mit der Cantorschen Tupelfunktion ist es uns möglich einem \(n\)-Tupel mit Elementen aus \(\mathbb{N}\) eine einzige, eindeutige Zahl aus \(\mathbb{N}\) zuzuordnen (Reduktion). Durch diese bijektive Abbildung von \(\mathbb{N}^n\rightarrow\mathbb{N}\) können wir uns auf die Berechnung von einstelligen Funktionen beschränken.
Einen weiteren prominenten Platz hat die Cantorsche Tupelfunktion bei dem Vergleich von Mengen: zwei Mengen sind gleichmächtig wenn man zwischen ihnen eine Bijektion herstellen kann.
Lernziel 2
Erläuterung der Abschlusseigenschaften berechenbarer Zahlenfunktionen
Ich bin mir hier gerade etwas unschlüssig: im Skript ist nicht mehr viel zu dem Thema drin, als der Satz zur Substitution, primitive Rekursion, \(\tilde{\mu}\) und der Umkehrfunktion. Vielleicht dann am besten an ein paar Beispielen?
Substitution
Zunächst haben wir zwei ggf. partielle Funktionen \(g:\subseteq\mathbb{N}^m\rightarrow\mathbb{N}\) und ggf. partielle Funktionen \(h_1\) bis \(h_m\) (d.h. so viele Funktionen wie der Definitionsbereich von \(g\) Parameter hat), mit \(h_1,…,h_m\subseteq\mathbb{N}^k\rightarrow\mathbb{N}\). Alle Funktionen sind berechenbar. Dann ist auch die Substitution \(Sub(g,h_1,…,h_m)\) berechenbar.
\(Sub(g,h_1,…,h_m)\subseteq\mathbb{N}^k\rightarrow\mathbb{N}\) ist definiert durch \(Sub(g,h_1,…,h_m)(x):=g(h_1(x),…,h_m(x))\)
Viel Zeug, oder? Keine Sorge, ist ganz easy.
Beispiel
\(g(x,y)=x+y\)
\(h_1(x,y,z)=x+y\)
\(h_2(x,y,z)=x+z\)
Die Substitution sieht nun so aus:
\(Sub(g,h_1,h_2)(x,y,z)=g(h_1(x,y,z),h_2(x,y,z))\).
Belegen wir unsere Funktion mit Werten: \(x=2,y=3,z=4\)
\(\begin{array} Sub(g,h_1,h_2)(2,3,4)&=g(h_1(2,3,4),h_2(2,3,4))\\&=g(5,h_2(2,3,4))\\&=g(5,6)\\&=11\end{array}\)
War doch trivial, oder (das wollte ich immer schon mal sagen!)?
Primitive Rekursion
Das ist ein klein wenig ekeliger als die Substitution, aber wir bekommen das gleich noch klein.
Auch hier haben wir zwei Funktionen \(g:\mathbb{N}^k\rightarrow\mathbb{N}\) und \(h:\mathbb{N}^{k+2}\rightarrow\mathbb{N}\), die berechenbar sind (Achtung: sie müssen auch total sein, denn sonst können wir nicht über diese „rekursivieren“). Wenn das der Fall ist, dann ist auch \(Prk(g,h)\) berechenbar.
\(Prk(g,h)\) ist definiert als:
\(f(x,0) = g(x)\)
\(f(x,y+1)=h(x,y,f(x,y))\)
Für alle \(x\in\mathbb{N}^k\) und \(y\in\mathbb{N}\). Man sieht bereits jetzt, dass wir rekursiv arbeiten. Noch deutlicher wird es an einem Beispiel.
Beispiel
\(g(x,z)=x+z\)
\(h(a,b,x,z)=a+b+x+z\)
Nehmen wir einfach mal \(y=3\) (\(3\)-malige Rekursion) und \(x=2,z=3,a=4,b=5\).
\(\begin{array} Prk(g,h)(2,3)&=f(2,3,3)\\&=h(2,3,2,f(2,3,2))\\&=h(2,3,2,(h(2,3,1,f(2,3,1))))\\&=h(2,3,2,(h(2,3,1,(h(2,3,0,f(2,3,0))))))\\&=h(2,3,2,(h(2,3,1,(h(2,3,0,g(2,3))))))\\&=h(2,3,2,(h(2,3,1,(h(2,3,0,5)))))\\&=h(2,3,2,(h(2,3,1,10)))\\&=h(2,3,2,16)\\&=23\end{array}\)
Versuchen wir das mit \(y=2\):
\(\begin{array} Prk(g,h)(2,2)&=f(2,3,2)\\&=h(2,3,1,f(2,3,1))\\&=h(2,3,1,(h(2,3,0,f(2,3,0))))\\&=h(2,3,1,(h(2,3,0,5)))\\&=h(2,3,1,10)\\&=16\end{array}\)
Viel Text, aber sicherlich gut nachzuvollziehen. Wir loopen und also durch die Funktionen mit einer festen Anzahl an Schleifen! In diesem Beitrag habe ich die primitive Rekursion etwas detaillierter betrachtet.
Und was ist wenn wir keine feste Anzahl an Schleifen haben können? Dann hilft uns unser \(\mu\)-Operator.
\(\tilde{\mu}\)Ist \(h\) mit \(h:\subseteq\mathbb{N}^{k+1}\rightarrow\mathbb{N}\) berechenbar, so ist es auch \(\tilde{\mu}(h)\). Wie ihr seht, auch hier ist \(h\) total. Was ist \(\tilde{\mu}\)?! \(\tilde{\mu}:\subseteq\mathbb{N}^{k}\rightarrow\mathbb{N}\). Es ist definiert durch:
\(\tilde{\mu}(h)(x)=\mu y[h(x,y)=0]\)
What the… Entspannung, Entspannung! Das ist nichts weiter als unsere \(\mu\)-Rekursion. Ich suche gerade im Skript ob wir das bereits irgendwo auf den vorherigen Seiten hatten… witzig. Hatten wir nicht. Das ist wirklich die erste Erwähnung. Und dann gleich ins kalte Wasser. Nicht schlimm, denn unser \(\tilde{\mu}\) ist nichts weiter, als der Operator, der es uns erlaubt auch Dinge zu berechnen, wo wir die genaue Anzahl an Schleifendurchläufen noch nicht wissen.
Und zwar indem wir unserer zu berechnende Funktion so weit umformen, dass wir beim Ende der Berechnung auf eine Nullstelle stoßen. Ich werde das nicht groß ausführen, sondern verweise ganz frech auf meinen alten Beitrag zum Thema.
Umkehrfunktion \(f^{-1}\)
Das schwerste zum Schluss. Hier gehen wir davon aus, dass \(f\) injektiv ist (wichtig!). Wir beschränken uns auch auf einstellige Funktionen. Warum? Na? Na? Genau: aufgrund der Cantorschen Tupelfunktion können wir das. Wenn diese Funktion also berechenbar ist, so ist es auch ihre Umkehrfunktion. Klingt logisch. Ist es auch.
Während für \(f\) Totalität und Injektivität gefordert ist, können wir bei \(f^{-1}\) bei einer ggf. partiellen Funktion rauskommen. Das liegt daran, dass wir in der Bildmenge von \(f\) evtl. Elemente haben, die wir mit unserer Funktion nicht „treffen“. Diese landen aber für \(f^{-1}\) dennoch in der Definitionmenge, sind aber nicht definiert. Damit ist \(f^{-1}\) eben partiell.
Beispiel
\(f(x) = x+5\) mit der Umkehrfunktion \(f^{-1}(\tilde{x})=\tilde{x}-5\). Setzen wir \(x=10\) und \(\tilde{x}=f(x)\), so haben wir:
\(f(10)=15\)
\(f^{-1}(15)=10\)
Passt.
Damit haben wir die Abschlusseigenschaften für berechenbare Zahlenfunktionen durch.
Antwort zum Lernziel: Funktionen, die sich aus den Funktionen Substitution, primitive Rekursion, \(\mu\)-Rekursion und der inversen Funktion zusammensetzen sind ebenfalls berechenbar.
Für die Substitution können die Funktionen auch partiell sein, für de primitive und \(\mu\)-Rekursion sind wir jedoch auf totale Funktionen angewiesen, da wir sonst nicht durch die Schleifendurchläufe kommen. Während wir bei der primitiven Rekursion zwingend die Anzahl der Schleifendurchläufe kennen müssen, ist es uns bei der \(\mu\)-Rekursion durch das „Nullsetzen“ der Funktion nicht wichtig. Es bricht eben ab wenn die Nullstelle gefunden ist. Wie lange es dauert wissen wir nicht.
Ersteres ist das Äquivalent zur \(LOOP\)-Schleife („tue etwas genau \(x\) Mal“), während die \(\mu\)-rekursion einer \(WHILE\)-Schleife („tue etwas bis…“) entspricht.
Für die inverse Funktion benötigen wir neben einer totalen Funktion \(f\) jedoch auch die Eigenschaft der Injektivität für \(f\), da wir nur auf maximal ein Element aus der Bildmenge abbilden dürfen, da sonst die Umkehrabbildung auf zwei unterschiedliche Elemente abbilden würde.
Lernziel 3
Definition der WHILE-Programme, Erläuterung ihrer Semantik und Angabe des Zusammenhangs zu berechenbaren Funktionen
Letztes Lernziel in dieser Kurseinheit. In diesem Beitrag sind die Details bereits herausgearbeitet, ich kümmere mich daher nur um die Definition und Semantik aus dem Skript. Das Fazit kann man wortwörtlich eig. auch für die Antwort zum Lernziel übernehmen. Also kümmern wir uns um die Syntax und die Semantik.
\(R_i+\) und \(R_i-\) sind \(WHILE\)-Programme
Dabei addiert \(R_i+\) im \(i\)-ten Registereine \(1\), \(R_i-\) subtrahiert eine \(1\) im \(i\)-ten Register.
IF \(R_i=0\) THEN \(P\) ELSE \(Q\)
Wir gehen davon aus, dass \(P\) und \(Q\) selbst \(WHILE\)-Programme sind.
WHILE \(R_i\neq 0\) DO \(P\)
Kennen wir auch schon. Solange das Register \(R_i\) nicht \(0\) ist, wird \(P\) ausgeführt.
Zusätzlich dazu haben wir noch unser kleines Tau \(\tau\). Dadurch weisen wir unseren oben beschriebenen Kommandos tatsächliche Funktionen auf der Datenmenge \(D=\mathbb{N}^{\mathbb{N}}\) zu, die wir bereits verbal beschrieben haben (sie ist die uns bekannte Datenmenge der Registermaschinen). Als Beispiel nehmen wir \(R_i+\) und \(R_i-\):
\(\tau(R_i+)(a_0,a_1,…):=(a_0,a_1,…,a_i+1,…,)\)
\(\tau(R_i-)(a_0,a_1,…):=(a_0,a_1,…,a_i-1,…,)\)
Wir können einem kompletten \(WHILE\)-Programm mittels \(\tau\) ebenfalls eine Ausgabe auf der Datenmenge \(D\) beschaffen: \(\tau(P)\). Und damit haben wir dann die komplette Registerausgabe unserer Maschine, die das Programm \(P\) berechnet. Damit schaffen wir es, dass unser Programm auf der Eingabecodierung einer Registermaschine operieren kann und uns auch eine Ausgabecodierung der Registermaschine liefert (siehe vorheriger Beitrag).
Noch eine kleine Definition für die \(WHILE\)-Berechenbarkeit
Wir nennen eine Funktion \(f:\mathbb{N}^k\rightarrow\mathbb{N}\) \(WHILE\)-berechenbar genau dann wenn gilt: \(f=AC(\tau(P)(EC))\)
Ähnliches Spiel wie im Beitrag zu KE1. Wir haben unterschiedliche Datenmengen für \(\tau\) und für die Flussdiagramme der Registermaschinen. Mit \(EC\) und \(AC\) wandelt wir diese nur ineinander um.
Das führt uns direkt zum Zusammenhang zu den berechenbaren Funktionen.
Beispiel
Funktion \(f(x,y)=x+y\) (operiert auf \(\mathbb{N}^2\rightarrow\mathbb{N}\))
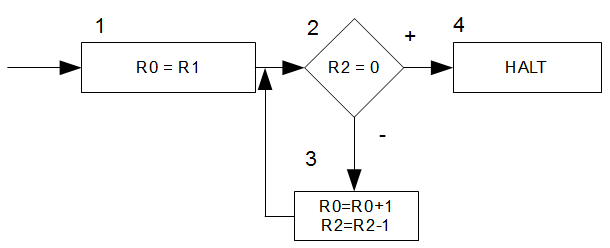
Dazu haben wir ein \(WHILE\)-Programm \(P\), welches uns die Funktion \(f\) berechnet. Es operiert auf \(\mathbb{N}^3\rightarrow\mathbb{N}^3\)
R0=R1;
WHILE R2 NOT 0 DO
R0+;
R2-;
END;
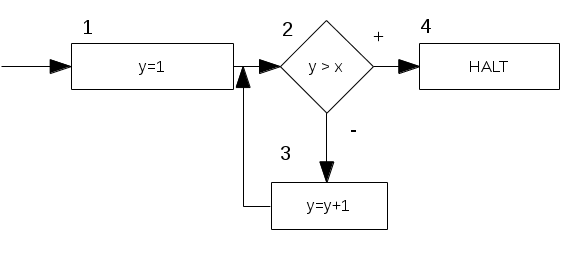
Wir können auch ein Flussdiagramm \(F\) einer Registermaschine \(M\) angeben, dass uns die gleiche Funktion raushaut.
Während das Flussdiagramm ebenfalls auf \(\mathbb{N}^3\rightarrow\mathbb{N}^3\) operiert, haben wir bei der Registermaschine jedoch \(\mathbb{N}^3\rightarrow\mathbb{N}\).
Damit gilt \(f=\tau(P)=f_M=f_F\). Oder doch nicht? Spielen wir das doch einfach mal mit \(x=2,y=3\) durch:
\(f(2,3)=5\)
\(\tau(P)(0,2,3)=(5,2,0)\)
\(f_M(0,2,3)=5\)
\(f_F(0,2,3)=(5,2,0)\)
Okay, die Berechnung ist anscheinend in Ordnung. Aber die Ausgabe von z.B. \(\tau(P)(0,2,3)=(5,2,0)\) ist sicher nicht gleich \(f_M(0,2,3)=5\) (siehe die Definition der Eingabe- und Ausgabecodierung von Registermaschinen im Lernziel 4 von Beitrag zu KE1).
Hier kommen unsere Funktionen \(EC\) und \(AC\) bei allen drei Berechnungsarten ins Spiel, die unsere Eingabe und unsere Ausgabe entsprechend umformen, so dass sie passen.
Definieren wir also z.B. \(AC\) für \(\tau(P)\) neu: \(AC(x,y,z)=x\), so haben wir
\(\begin{array}{}AC(\tau(P)(0,2,3))&=AC(5,2,0)\\&=5\end{array}\)
Damit würde \(f_M=AC(\tau(P))\) wieder passen.
Das spannende also daran ist, dass es durchaus vorkommen kann, dass unser Flussdiagramm, unsere Registermaschine oder unser \(WHILE\)-Programm nicht alle auf einer Datenmenge operieren, sondern alle auf unterschiedlichen Mengen (warum auch immer). Um aber zu sagen, dass z.B. \(\tau(P)=f_M\) gilt, müssen wir sie evtl. umgestalten. Für \(\tau(P)=f_F\) brauchen wir das hingegen – wie wir oben gesehen haben – nicht.
Lange Rede, kurzer Sinn:
Zu jedem \(WHILE\)-Programm gibt es ein Flussdiagramm einer Registermaschine mit \(\tau(P)=f_F\)
Zu jedem Flussdiagramm einer Registermaschine gibt es ein \(WHILE\)-Programm mit \(f_F=\tau(P)\) mit einer \(WHILE\)-Schleife.
Damit gilt: die Funktion \(f\) ist \(WHILE\)-berechenbar genau dann wenn sie Register-berechenbar ist.
Antwort zum Lernziel: die \(WHILE\)-Programme bestehen aus bedingten Anweisungen (\(IF\)) und Schleifen (\(WHILE\)), sowie Anweisungen zum Register hoch- oder runterzählen und Hintereinanderausführungen von Anweisungen.
Der Zusammenhang zu berechenbaren Funktionen kommt daher, dass man zu jedem \(WHILE\)-Programm eine Registermaschine angeben kann, die die selbe Funktion berechnet und zu jeder Registermaschine ein \(WHILE\)-Programm existiert.
\(WHILE\)-Programme sind mächtiger als \(LOOP\)-Programme: man kann \(LOOP\)-Schleifen mit \(WHILE\)-Schleifen nachbilden, aber nicht anders herum, da man die Anzahl der Schleifendurchläufe im Vorfeld nicht bei jeder \(WHILE\)-Schleife kennt.
Die \(LOOP\)-Anwendungen sind das Äquivalent zur primitiven Rekursion, während die \(WHILE\)-Programme erst mit dem \(\mu\)-Operator (durch „Nullsetzen“ der Funktion) nachgebildet werden können.