Inhaltsverzeichnis
- Berechenbarkeit von Zahlen- und Wortfunktionen
- Entscheidbarkeit (rekursiv) und Semi-Entscheidbarkeit (rekursiv aufzählbar)
- Erstes und zweites Diagonalargument von Cantor
Im Skript wird dieses Thema schnell durchgekauft. Persönlich halte ich es jedoch für sehr wichtig, sich diese Begrifflichkeiten unbedingt zu merken. Also fangen wir auch direkt an:
Berechenbarkeit
Noch einmal kurz als Wiederholung bzgl. Berechenbarkeit: dem Begriff selbst liegen Berechnungsmodelle zugrunde. Wir haben hier die LOOP-Berechenbarkeit (primitiv rekursive Funktionen) und die WHILE-Berechenbarkeit ($$\mu$$-rekursive Funktionen). Während jedes LOOP-Programm durch ein WHILE-Programm ersetzt werden kann, kann nicht jedes WHILE-Programm durch ein LOOP-Programm ersetzt werden, d.h. die LOOP-Programme sind eine echte Untermenge der WHILE-Programme. Wann ist eine Funktion denn nun berechenbar? Genau dann:
Eine (ggf. partielle) Zahlenfunktion $$f : \subseteq \mathbb{N}^k \rightarrow \mathbb{N}$$ ist genau dann berechenbar, wenn es eine Registermaschine $$M$$ gibt, die die Funktion berechnet. Wenn also $$f = f_M$$ gilt.
Und was ist mit Wortfunktionen für Turing-Maschinen?
Eine (ggf. partielle) Wortfunktion $$g : \subseteq (\Sigma^*)^k \rightarrow \Sigma^*$$ ist genau dann berechenbar, wenn es eine Turing-Maschine $$T$$ gibt, die die Funktion berechnet. Wenn also $$g =g_T$$ gilt.
Aber eig. brauchen wir die Turing-Maschinen garnicht. Warum? Zauberwort: Standardnummerierung. Wir können dadurch die Berechenbarkeit von Worten auf die Berechenbarkeit von Zahlen zurückführen indem wir die Wortfunktionen mittels Standardnummerierung in Zahlen codieren und diese mit Registermaschinen berechnen. Da die Standardnummerierung bijektiv ist, können wir den Spaß auch anders herum aufziehen und unsere Zahlenfunktionen durch Turing-Maschinen berechnen lassen nachdem wir die Zahlenfunktionen in Worte codiert haben.
Schaut dazu in den entsprechenden Beitrag für die Kurseinheit 4. Dort wird das Thema dann etwas genauer behandelt. Wichtig ist, dass man sich den Zusammenhang zwischen Wort- und Zahlenfunktionen und das Bindeglied (Standardnummerierung) zwischen diesen merkt.
(Semi-) Entscheidbarkeit
Wir unterscheiden hier die Entscheidbarkeit und die Semi-Entscheidbarkeit. Ihr Kern ist die charakteristische Funktion. Wozu brauchen wir sie? Der Begriff „Entscheidbarkeit“ ist auf Mengen fokusiert, für uns sind aber eher Funktionen spannend, wo nur der Begriff „Berechenbarkeit“ verwendet wird. Die charakteristische Funktion ist das Bindelglied zwischen diesen Mengen und der Funktionen (den Satz habe ich aus dem Buch von Dirk W. Hoffmann geklaut). Formalisieren wir das:
Eine Menge $$ T \subseteq M$$ ist entscheidbar/rekursiv wenn die charakteristische Funktion $$\chi_T: M \rightarrow \{0,1\}$$ definiert durch
$$\chi_T(t)=\begin{cases} 1, & \mbox{ falls } t \in T \\ 0, & \mbox{ sonst}\end{cases}$$
berechenbar ist (Achtung: sie muss berechenbar sein!)
Was ist damit gemeint? Damit ist gemeint, dass man hier eindeutig entscheiden kann ob ein Element $$t$$ aus der Menge $$M$$ in der Menge $$T$$ sind. Es wird nach endlicher Zeit also eindeutig entschieden ob JA oder NEIN.
Beispiel: ob eine Zahl gerade ist oder eine Primzahl ist, ist entscheidbar/rekursiv (Wikipedia). Diese Zahlen sind auch rekursiv aufzählbar (denn ich kann sie ja aufzählen).
Und nun zur Semi-Entscheidbarkeit/rekursiver Aufzählbarkeit.
Eine Menge $$T$$ ist semi-entscheidbar/rekursiv aufzählbar wenn die partielle charakteristische Funktion $$\chi^{‚}_T: M \rightarrow \{1\}$$ definiert durch
$$\chi^{‚}_T(t)=\begin{cases} 1, & \mbox{ falls } t \in T \\ \perp, & \mbox{ sonst}\end{cases}$$
Diesen Spaß nennt man also semi-entscheidbar. D.h. wenn das Element $$t$$ aus $$M$$ in $$T$$ liegt, so wird nach endlicher Zeit ein JA (oder auch NEIN wenn man anders herum testen möchte) ausgegeben. Wenn nicht, so hängen wir ggf. in einer Endlosschleife. Der Unterschied hier ist, dass wir nicht wissen ob wir einfach noch länger warten müssen bis wir (irgendwann) ein JA/NEIN bekommen oder wir tatsächlich in einer Endlosschleife sind.
Beispiel: Das Halteproblem (ob alle Paare (Turingmaschine, Eingabe)) für alle Eingaben und Turingmaschinen halten ist semi-entscheidbar/rekursiv aufzählbar, aber nicht entscheidbar/rekursiv. Denn für einige Eingaben kann eine Turingmaschine in eine Endlosschleife laufen und wir können nicht mit Sicherheit sagen ob sie nicht doch vielleicht irgendwann hält. Damit ist das Halteproblem eben nur rekursiv aufzählbar, denn wir können die Menge der Paare mit der Eigenschaft ja aufzählen.
Achtung: jede rekursiv aufzählbare/semi-entscheidbare Menge ist abzählbar. Aber nicht jede abzählbare Menge ist rekursiv aufzählbar/semi-entscheidbar. Z.B. ist die Menge der falschen Formeln einer PL1-Sprache (dazu in einem späteren Beitrag mehr) abzählbar, jedoch nicht entscheidbar/rekursiv aufzählbar. Ebenso ergeht es uns mit dem Busy Beaver Problem (auch hierzu folgt später ein Beitrag). Das Halteproblem, wie im Abschnitt vorher angegeben, ist ein Beispiel für die andere Richtung.
Abzählbarkeit: erstes und zweites Diagonalargument (Cantor)
Wir bezeichnen Mengen als abzählbar wenn diese die gleiche Mächtigkeit hat, wie $$\mathbb{N}$$. In dem Eintrag für die Cantorsche Tupelfunktion wir beschrieben, wie man prüft ob zwei Mengen gleichmächtig sind. Wir prüfen also den Fall $$\left| M \right| = \left| \mathbb{N} \right|$$? Um das zu tun müssen wir eine bijektive Abbildung $$f: M \rightarrow \mathbb{N}$$ aufzeigen, die jedem Element aus $$M$$ eindeutig ein Element aus $$\mathbb{N}$$ zuordnet. Durch die Bijektivität ist diese Funktion natürlich umkehrbar und wir können zu einem Element aus $$\mathbb{N}$$ wieder eindeutig ein Element aus $$M$$ zuordnen. Das nennt man das erste Diagonalisierungsargument von Cantor.
Wie in dem oben verlinkten Beitrag können wir z.B. eine bijektive Abbildung $$f: \mathbb{Z} \rightarrow \mathbb{N}$$ angeben und so zeigen, dass die ganzen Zahlen ($$\mathbb{Z}$$) genauso mächtig sind wie die natürlichen Zahlen ($$\mathbb{N}$$) obwohl die ganzen Zahlen gefühlt mehr Zahlen enthalten als die natürlichen Zahlen. Ebenso können wir durch diese Cantorsche Tupelfunktion $$n$$-Tupel aus $$\mathbb{N}^n$$, z.B. $$(1,5)$$ aus $$\mathbb{N}^2$$ auf eine einzige Zahl aus $$\mathbb{N}$$ abbilden. Das gleiche geht für Tripel usw. Damit ist bewiesen, dass der $$n$$-dimensionale Raum $$\mathbb{N}^n$$ gleichmächtig zu $$\mathbb{N}$$ ist, egal welches $$n$$ wir wählen.
Gibt es ein Beispiel für nicht abzählbare Mengen? Ja: die reellen Zahlen sind nicht gleichmächtig zu $$\mathbb{N}$$ und damit auch nicht abzählbar. Es gibt also keine bijektive Abbildung $$f: \mathbb{R} \rightarrow \mathbb{N}$$. Cantor bewies dies 2x. Sein letzter Beweis ist einfacher, deswegen möchte ich diesen hier kurz skizzieren: es ist sein zweites Diagonalisierungsargument.
Beispiel: zweites Diagonalisierungsargument von Cantor
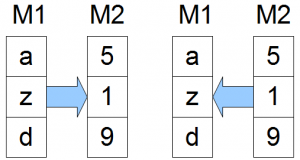
Zunächst einmal sollten wir uns klar machen, was wir mit einer bijektiven Abbildung denn eigentlich machen. Eine bijektive Abbildung kann es nur zwischen zwei gleichmächtigen Mengen geben. Im vorherigen Beitrag hatten wir z.B. $$M_1 = \{a,z,d\}$$ und $$M_2 = \{5,1,9\}$$. Wir geben eine bijektive Abbildung für diese Mengen an: $$f: M_1 \rightarrow M_2$$ definiert durch $$a=5, z=1, d=9$$ (Umkehrabbilung $$f^{-1}$$ ist dann genau umgekehrt).
Wir wir sehen können wir zu einem Element aus $$M_1$$ eindeutig ein Element aus $$M_2$$ zuordnen und aufgrund der Eindeutigkeit geht es auch anders herum und wir bekommen ein eindutiges Element aus $$M_1$$ zu einem Element aus $$M_2$$. Damit sind die beiden Mengen gleichmächtig.
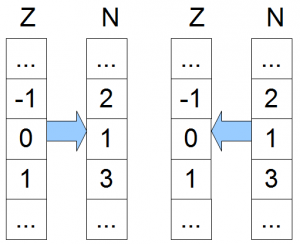
Eine bijektive Abbildung können wir auch für $$\mathbb{Z}$$ und $$\mathbb{N}$$ angeben und zeigen, dass diese Mengen ebenfalls gleichmächtig sind. Wir verwenden wieder das Beispiel aus dem Beitrag für die Cantorsche Tupelfunktion: $$ f:\mathbb{Z} \rightarrow \mathbb{N}$$ definiert durch:
$$f(x) = \begin{cases} -2x, & \mbox{ falls } x<0\\ 2x+1, & \mbox{ falls } x\geq 0\end{cases}$$+
Die Umkehrabbildung ist:
$$f^{-1}(x) = \begin{cases} -x/2, & \mbox{ wenn x gerade }\\ (x-1)/2, & \mbox{ wenn x ungerade}\end{cases}$$
Unsere Abbildung sieht nun für ein paar Zahlen so aus:
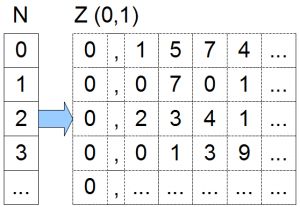
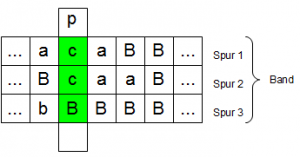
Wie wir sehen, sind auch diese Mengen gleichmächtig. Wir haben wieder eine eindeutige Zuordnung zwischen den Elementen aus $$\mathbb{R}$$ und $$\mathbb{N}$$. Probieren wir das gleiche doch für $$\mathbb{N} \rightarrow \mathbb{R}$$. Es reicht uns sogar einfach nur alle reellen Zahlen zwischen 0 und 1 anzuschauen (also: 0,72636…, 0,12238383…., …). Für eine bijektive Abbildung müssen wir allen diesen Zahlen dann natürliche Zahlen zuordnen. Dazu basteln wir uns eine Matrix und eine willkürliche Abbildungsfunktion, die allen Zahlen aus $$\mathbb{N}$$ eine Zahl aus dem Intervall $$(0,1)$$ aus $$\mathbb{R}$$ zuordnet.
Wir weisen z.B. dem Definitionswert $$0$$ aus $$N$$ den Funktionswert $$0,1574…$$, dem Definitionswert $$1$$ die $$0,0701…$$ usw. zu. Mit $$…$$ haben wir angedeutet, dass die Matrix aus unendlich vielen Zeilen und die Dezimalbruchdarstellung aus unendlich vielen Nachkommastellen besteht. Lasst euch von den Kästchen nicht verwirren, $$0,1574…$$ ist ein Element, die Kästchen dienen nur dem, was wir gleich vor haben: wir zeigen jetzt mit dem Diagonalisierungsargument, dass die Matrix nie vollständig sein kann, dass es also einen Wert zwischen $$0$$ und $$1$$ aus $$\mathbb{R}$$ gibt, auf den wir nicht abbilden.
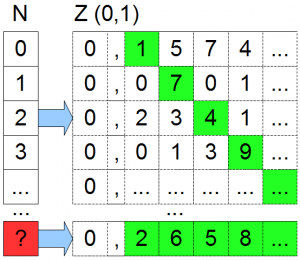
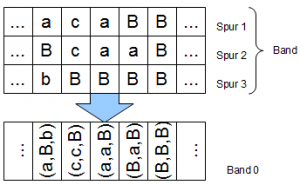
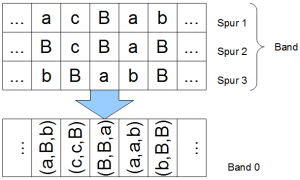
Wir führen einen Widerspruchsbeweis: nehmen wir an die Matrix sein vollständig und wir haben alle Zahlen aus $$\mathbb{R}$$ zwischen 0 und 1 in Dezimaldarstellung durchnumemriert. Wir basteln uns einen neuen Funktionswert, der von allen anderen Funktionswerten verschieden ist: wir verwenden die diagonalen Elemente der Matrix (grüne Markierung) und erhöhen oder erniedrigen sie um 1 ($$<5$$: neue Zahl wird erhöht, $$\geq 5 $$: neue Zahl wird erniedrigt) und verwenden diese Zahlen als Nachkommastellen unseres neuen Eintrags. Damit ist sichergestellt, dass wir diesen Eintrag noch nicht als Funktionswert in unserer Matrix haben, denn die reelle Zahl in der $$i$$-ten Zeile unserer Matrix unterscheidet sich min. in der $$i$$-ten Stelle von unserer neuen Zahl (wir haben sie ja erniedrigt oder erhöht).
Damit ist $$0,2658…$$ unser neuer Eintrag, der definitiv noch nicht un unserer Matrix ist. Soweit so gut, nur wie wird er jetzt mit einer Zahl aus $$\mathbb{N}$$ nummeriert?! Wir sind doch von der Vollständigkeit unserer Matrix ausgegangen und haben damit doch alle unsere Elemente aus $$\mathbb{N}$$ ausgeschöpft, haben aber trotzdem ein neues aus $$\mathbb{R}$$, dass wir nummerrieren müssen! Also: Widerspruch! Damit sind $$\mathbb{R}$$ und $$\mathbb{N}$$ nicht gleich mächtig, $$\mathbb{R}$$ ist sogar deutlich größer, da wir ja nicht einmal das Intervall $$(0,1)$$ mit allen Elementen aus $$\mathbb{N}$$ nummerrieren konnten. $$\mathbb{R}$$ und $$\mathbb{N}$$ stehen also für zwei unterschiedliche Unendlichkeiten. Ein sehr cooler Beitrag auf youtube zeigt das nochmal in bewegten Bildern.
So schließt sich auch der Kreis zu den Funktionen: die Menge aller berechenbaren mehrstelligen Wortfunktionen ist ebenfalls abzählbar. Warum? Weil wir die Menge der mehrstelligen Wortfunktionen in einstellige Wortfunktionen überführen können, diese durch die Standardnummerierung in einstellige Zahlenfunktionen überführt wird und wir diese anschließend durchnummerieren können.