Kategorie: Theoretische Informatik

Update: mir sind einige Schnitzer beim Halteproblem aufgefallen, die ich mittlerweile ausgeräumt haben sollte. Hoffe ich. Auch habe ich den Beitrag um den Beweis zum Bild- und Projektionssatz erweitert (der nun in einem eigenen Beitrag steht), was ihn leider um ein paar Seiten verlängert hat.

Es gibt insg. drei vier Beiträge zur KE6.

• TIA: Rekursive und rekursiv-aufzählbare Mengen (Lernziele KE6, 1/4)
• TIA: Bild- und Projektionssatz (Lernziele KE6 2/4)
• TIA: Halte- Äquivalenz- und Korrektheitsproblem, Reduzierbarkeit, Satz von Rice (Lernziele KE6, 3/4)
• TIA: Gödel’scher Unvollständigkeitssatz (Lernziele KE6, 4/4)

Es sind nur noch ein paar Lernziele übrig, halten wir uns also ran.

Lernziel 7a

Halte- und Selbstanwendbarkeitsproblem

Die beiden Probleme sind definiert als die Mengen:

\(K_\varphi := \{i \in \mathbb{N} \mid \varphi_i(i) \mbox{ existiert}\}\) \({K_{\varphi}}^0 := \{(i,x) \in \mathbb{N}^2 \mid \varphi_i(x) \mbox{ existiert}\}\)

Wichtig: Komplemente \(\mathbb{N}\setminus{}K_\varphi\) und \(\mathbb{N}^2\setminus{K_{\varphi}}^0\) sind nicht r.a.

In den meisten Fällen wird zunächst gezeigt, dass das spezielle Halteproblem nicht entscheidbar ist. Anschließend wird das spezielle Problem auf das allgemeine zurückgeführt („Wenn schon nicht entscheidbar ist, ob eine Maschine auf ihrem eigenen Wort hält, wie kann man dann entscheiden ob es das für alle Eingabeworte tut?“).

Fangen wir daher auch zunächst mit dem speziellen Halteproblem an.

Spezielles Halteproblem

Das ist die Fragestellung ob Die Maschine mit der Nr. \(i\) bei der Eingabe von \(i\) (die Maschine können wir ja als Eingabewort codieren, wie wir ja durch die Standardnummerierung und das utm-Theorem wissen) hält oder nicht.

Diese Problem wird auch das Selbstanwendbarkeitsproblem genannt. Im Skript steht dazu:

„Das Selbstanwendbarkeitsproblem für \(\varphi\) ist rekursiv unlösbar“.

Es bedeutet nichts anderes, als dass die Menge \(K_\varphi\) zwar r.a. ist, aber nicht rekursiv/entscheidbar. Wir können nämlich nicht entscheiden ob eine Maschine existiert, die bei der Eingabe ihrer eigenen Gödelnummer hält oder nicht. Warum?

Es gibt hier, nehmen wir es genau, zwei Möglichkeiten. Beide funktionieren durch Widerspruch, indem gezeigt wird, dass es so eine Maschine nicht geben kann, die dieses Problem entscheidet. Ihr könnt euch also entscheiden welche Art von Darstellung euch eher zusagt.

Da ich einen anschaulichen Beweis für das allgemeine Problem brauchte, habe ich mir die graphische Variante dafür aufgespart und vertröste euch auf hübsche Bildchen im nächsten Abschnitt.

Zunächst ein sehr schöner (wie ich finde) Widerspruchsbeweis für das spezielle Halteproblem.

Klassischer Widerspruchsbeweis für das spezielle Halteproblem

Es gibt also noch eine Methode, die weniger graphischen Umgang mit Open Office Produkten erfordert, wir damit aber dennoch eine schöne, logische Kette von Schlüssen ziehen können und dabei zu einem Widerspruch gelangen.

Dazu bemühe ich das Barbier-Paradoxon wie Socher in seinem Buch (siehe oben rechts) und zitiere ihn:

Dieser klassische Widerspruchsbeweis hat große Ähnlichkeit mit dem Barbier-Problem, der sog. Russelschen Antinomie:

Man kann einen Barbier als einen definieren, der all jene und nur jene rasiert, die sich nicht selbst rasieren.

Die Frage ist: Rasiert der Barbier sich selbst?

Wenn man versucht die Frage zu beantworten, landet man stets in einem Widerspruch. Wie bei der folgenden Überlegung für das spezielle Halteproblem:

• Nehmen wir an die Männer, die sich selbst rasieren sind unsere Turing-Maschinen \(M_i\), die sich selbst, also \(i\), akzeptieren. Sie halten bei der Eingabe ihrer eigenen Gödelnummer. Formal:

\(M_i(i)\) existiert.

Annahme: es gibt eine Maschine \(H\), die \(1\) ausgibt wenn die Maschine \(M_i\) bei ihrer Gödelnummer hält und ansonsten in eine Endlosschleife gerät. Formal:

\(H(i)=\begin{cases} 1, & \mbox{ falls } M_i(i)\mbox{ existiert} \\ \perp, & \mbox{ sonst}\end{cases}\)

• Nun konstruieren wir die Maschine \(B\) (den Barbier), diese sagt uns ob die Maschine \(M_i\) bei der Eingabe ihrer Gödelnummer \(i\) hält oder nicht indem er die Maschine \(H\) mit einer Gödelnummer startet. Gibt uns \(H\) eine \(1\) zurück, so gerät \(B\) in eine Endlosschleife. Gerät \(H\) in eine Endlosschleife, akzeptiert \(B\) die Ausgabe. Formal:

\(B(i)=\begin{cases} 1, & \mbox{ falls } H(i)=\perp \\ \perp, & \mbox{ falls }H(i)=1\end{cases}\)

In anderen Worten:

\(B\) akzeptiert \(M\) genau dann wenn \(M\) sich nicht selbst akzeptiert

Da wir im Endeffekt ja \(M=B\) haben wenn wir \(B\) auf sich selbst ausführen, so ist das Dilemma, in welches wir laufen genau das Barbier-Paradoxon von Russel:

\(B\) akzeptiert \(B\) genau dann wenn \(B\) sich nicht selbst akzeptiert

Fall 1: \(B\) hält, wir starten \(B\) mit seiner eigenen Nr. \(i\)

\(B(i)=1\Rightarrow H(i)=\perp\Rightarrow M_i(i)=\perp\Rightarrow B(i)=\perp\). Widerspruch!

Fall 2: \(B\) hält nicht, wir starten \(B\) also mit seiner eigenen Nr. \(i\)

\(B(i)=\perp\Rightarrow H(i)=\perp\Rightarrow M_i(i)=1\Rightarrow B(i)=1\). Widerspruch!

Denn in beiden Fällen ist ja \(B=M\)

Damit kann es keine Maschine geben, die das spezielle Halteproblem entscheidet.

Obwohl wir den Regeln der Logik gefolgt sind, stießen wir auf einen Widerspruch. Das bedeutet, dass unsere Grundannahme, so eine Maschine \(B\) könne existieren, falsch war.

Kommen wir nun zum allgemeinen Halteproblem.

Allgemeines Halteproblem

Zum speziellen Halteproblem, also der Frage ob eine Maschine \(M_i\) angewendet auf sich selbst hält oder nicht gibt es noch die allgemeine Version mit folgender, formalen Definition (Wiederholung von oben):

\({K_{\varphi}}^0 := \{(i,x) \in \mathbb{N}^2 \mid \varphi_i(x) \mbox{ existiert}\}\)

Anders ausgedrückt:

Hält die Maschine \(M_i\) bei der Eingabe von \(x\)?

Zuerst nochmal die Wiederholung: wann ist eine Menge \(A\subseteq{B}\) entscheidbar? Genau dann wenn neben \(A\) auch das Komplement \(B\setminus{A}\) semi-entscheidbar ist.

Die Menge \({K_{\varphi}}^0\) ist selbst r.a.. Warum? Wenn eine Maschine \(i\) bei der Eingabe \(x\) hält, dann hält sie. Wir haben in jedem Fall bei einem positiven Entscheid eine Ausgabe und damit einen positiven Entscheid (sofern es den gibt). Ansonsten rechnet die Maschine ewig weiter.

Wir können die Elemente der positiven Menge \((i,x)\) („Hält Maschine \(i\) bei Eingabe von \(x\)„) also „aufzählen“. Wenn sie denn wirklich hält. Die Elemente der anderen Menge, die Menge der Kombinationen von \((i,x)\), wo eine Maschine \(M_i\) bei der Eingabe von \(x\) nicht hält aber eben nicht (im ungünstigsten Fall rechnet die Maschine \(i\) bei der Eingabe von \(x\) nämlich ewig).

Diese positive Menge nennen wir eben

\({K_{\varphi}}^0\)

Die negative Menge ist das Komplement davon, nämlich:

\(\mathbb{N}^2\setminus{K_{\varphi}}^0\)

Während die obere, wie erwähnt, semi-entscheidbar/rekursiv-aufzählbar ist, ist es das Komplement leider nicht. Wäre sie das, so wären alle unsere Probleme gelöst und die Menge \({K_{\varphi}}^0\) wäre entscheidbar/rekursiv.

Formal ausgedrückt müsste für die Semi-Entscheidbarkeit von \(\mathbb{N}^2\setminus{K_{\varphi}}^0\) die „halbe“ charakteristische Funktion berechenbar sein:

\(\chi^{‚}_{{{K_{\varphi}}^0}(i,x)}=\begin{cases} 1, & \mbox{ falls }i\text{ bei der Eingabe von }x\text{ haelt}\\ \perp, & \mbox{sonst}\end{cases}\)

\(\chi^{‚}_{{K_{\varphi}}^0}\) ist, wie wir gemerkt haben berechenbar. Damit ist unsere Menge \({K_{\varphi}}^0\) aber leider nur r.a.

Wäre aber nicht schlimm: Wenn wir zeigen können, dass \(\mathbb{N}\setminus{K_{\varphi}}^0\) auch r.a. ist, so wäre \({K_{\varphi}}^0\) der Definition nach entscheidbar. Warum das nicht geht, zeigen wir jetzt.

\(\chi^{“}_{{{\mathbb{N}^2\setminus K_{\varphi}}}^0(i,x)}=\begin{cases} 1, & \mbox{ falls }i\text{ bei der Eingabe von }x\text{ nicht haelt}\\ \perp, & \mbox{sonst}\end{cases}\)

Da wir nicht wissen, ob die Maschine \(i\) bei der Eingabe von \(x\) niemals hält oder einfach nur noch nicht gehalten hat weil sie noch rechnet, können wir die Funktion \(\chi^{“}_{{{\mathbb{N}^2\setminus K_{\varphi}}}^0(i,x)}\) nicht berechnen. Das leuchtet eig. schon direkt ein.

Aber um das alles noch komplett ad absurdum zu führen tun wir folgendes:

Beweis anhand des speziellen Halteproblems

Wie wir gesehen haben, ist das spezielle Halteproblem nicht lösbar. Daraus folgt auch ganz simpel, dass es keine Maschine \(H(i,x)\) geben kann, die für jedes \(x\) entscheidet ob Maschine \(M_i\) bei der Eingabe von \(x\) hält oder nicht.

Warum? Weil eines der \(x\) auch die Nummer der Maschine \(M_i\) selbst ist, d.h. \(x=i\). Und wir wir haben im letzten Abschnitt gesehen, dass genau das nicht geht.

Einfach, nicht? Und wenn wir die Unlösbarkeit des allgemeinen Halteproblems beweisen wollen, ohne zuerst die Unlösbarkeit des speziellen Halteproblems bewiesen zu haben? Dann machen wir das mit einem klassischen, graphischen Widerspruchsbeweis durch Diagonalisierung.

Graphischer Widerspruchsbeweis mittels Diagonalisierung

Dieser Beweis ist dem Diagonalverfahren von Cantor sehr ähnlich und ist im Grunde auch ein Beweis für das spezielle Halteproblem.

Was haben wir vor? Wir machen hier einfach eine Annahme, dass es eine best. Maschine gibt und zeigen, dass es sie nicht geben kann. Wir führen unsere Annahme also zu einem Widerspruch. Ganz einfach.

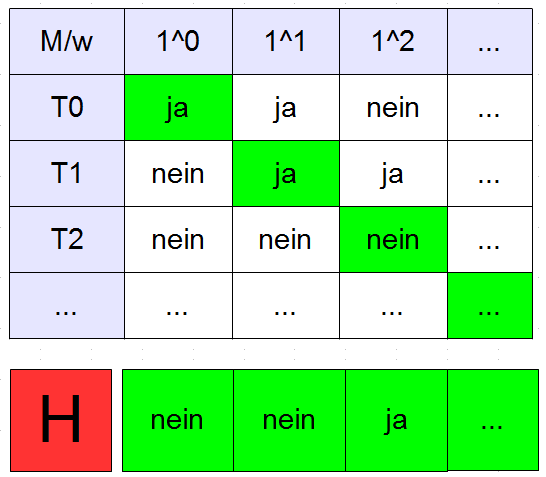
Konstruieren wir zunächst eine Matrix, wo wir auf der \(y\)-Achse alle unsere Maschinen aufsteigend ihrer Gödelnummer \(0,…,n\) auflisten. Auf der \(x\)-Achse stehen alle Eingabeworte \(1^0, …, 1^x\). In den Zellen steht dann drin ob die Maschine für die Eingabe des Wortes hält oder nicht:

Gäbe es eine Maschine, die entscheiden könnte ob eine andere Maschine bei der Eingabe hält, so würde sie uns genau diese Matrix konstruieren.

In dieser Matrix stehen alle Maschinen und alle Worte drin. Nun basteln wir uns eine neue Maschine \(H\), welche zum Eingabewort \(1^i\) das Matrixelement \((i,i)\) berechnet und sich genau entgegengesetzt zur Maschine \(T_i\) verhält (sie hält wenn dort \(T_i\) bei der Eingabe von \(i\) nicht halten würde und läuft in eine Endlosschleife wenn dort \(T_i\) halten würde).

Diese neue Maschine \(H\) ist ja selbst eine Turing-Maschine. Damit müssten wir sie ja in unserer Matrix vorfinden. Tun wir aber nicht, denn egal wo wir nachschauen: unsere neue Maschine hat bei seinen Berechnungen immer mindestens einen unterschiedlichen Ergebniswert als Maschine \(T_i\) beim Wort \(i\) und ist daher tatsächlich neu. Was aber nicht sein kann, denn wir haben in der Matrix nach Definition alle Turingmaschinen bereits drin.

Widerspruch!

Etwas abstrakt, aber durchaus logisch nachvollziehbar. Das ist das schöne an Widerspruchsbeweisen. Falls Ihr das nicht direkt beim Lesen nachvollziehen konntet: schreibt euch das einfach auf’s Papier. Dann kommt der „Aha-Effekt“, versprochen.

Wem das zu abstrakt war, der schaue sich nochmal folgenden Beitrag an. Dort wird die Überabzählbarkeit von \(\mathbb{R}\) mit dem gleichen Verfahren bewiesen.

Zusammenfassend wird die Beweisführung häufig nach folgendem Muster geführt:

• spezielles Halteproblem (auch Diagonalsprache genannt), wo die Maschine auf sich selbst angewendet wird, ist nicht entscheidbar. Gezeigt wird es meist durch Diagonalisierung. 
• Komplement dieser Menge ist nicht einmal semi-entscheidbar, da wir dazu diese „Diagonalisierungsmaschine“ bräuchten. Und diese kann es ja nicht geben.
• Daraus folgt, dass das allgemeine Halteproblem auch nicht entscheidbar ist. Denn sonst wäre sein Komplement semi-entscheidbar. Das geht aber nicht, da eine Eingabe das eigene Wort der Maschine ist. Und wie wir bewiesen haben, kann es keine Maschine geben, die entscheidet ob eine Maschine angewendet auf sich selbst hält oder nicht.

Antwort zum Lernziel: das Halteproblem bezeichnet die Fragestellung ob eine Maschine bei der Eingabe eines Eingabewertes hält oder nicht. Es ist nur semi-entscheidbar/rekursiv-aufzählbar.

Bei dem speziellen Halteproblem ist die Fragestellung ob eine Maschine angewendet auf seine eigene Gödelnummer hält oder nicht. Diese Menge ist ebenfalls nur semi-entscheidbar/rekursiv-aufzählbar.

Die Komplemente dieser Fragestellungen sind nicht semi-entscheidbar/rekursiv-aufzählbar (wir können nicht wissen ob die Maschine nie hält oder nur noch rechnet und doch noch halten wird). Wären sie das, so wären auch die Halteprobleme entscheidbar/rekursiv.

Lernziel 8

Erklärung der Reduzierbarkeit und Methode der Reduktion

Reduzierbarkeit, formal definiert heißt:

\(A \leq B : \Longleftrightarrow \exists f \in R^{(1)}. A = f^{-1}[B]\)

\(A\) ist reduzierbar auf \(B\) genau dann wenn die Menge \(A\) eine Urbildmenge von \(B\) unter \(f\) ist.

Schon wieder sowas komisches. Das bekommen wir aber auch noch klein. Zunächst einmal haben wir eine wunderschöne, einstellige, rekursive Funktion \(f\), welches uns zu einem \(x\) aus \(A\) ein Bild liefert, welches selbst in \(B\) liegt. Damit ist \(A\) die Urbildmenge von \(B\).

Etwas formaler ausgedrückt und wortwörtlich aus dem Skript:

\((x \in A \Rightarrow f(x) \in B)\) und \((x \notin A \Rightarrow f(x) \notin B)\).

Liegt ein \(x\) in \(A\), so liegt auch sein Bild (Funktionswert) \(f(x)\) in \(B\). Liegt ein \(x\) nicht in \(A\), so liegt auch sein Bild nicht in \(B\).

Die Abschlusseigenschaften der Reduzierbarkeit sind (wir haben als Annahme 3 Mengen \(A,B,C \subseteq \mathbb{N}\)) sind ähnlich denen aus Abschlusseigenschaften rekursiver Mengen:

1. \(A \leq B\) und \(B \leq C \Rightarrow A \leq C\)

Erläuterung: Ist \(A\) reduzierbar auf \(B\) und \(B\) reduzierbar auf \(C\), so ist auch \(A\) reduzierbar auf \(C\). Simple Transitivität.

2. \(A \leq B\Longleftrightarrow\mathbb{N}\setminus{A}\leq\mathbb{N}\setminus{B}\)

Erläuterung: Die Transitivität gilt auch für Komplemente von \(A\) und \(B\).

3. \(A \leq B\) und \(B\) rekursiv \(\Rightarrow A\) rekursiv

4. \(A \leq B\) und \(B\) rekursiv aufzählbar \(\Rightarrow A\) rekursiv aufzählbar

Erläuterung: Auch übernimmt die reduzierte Menge \(A\) die Eigenschaften der Menge \(B\). Ist Menge \(B\) r.a. oder rekursiv, so ist es auch die Menge \(A\) wenn man sie erfolgreich auf \(B\) reduzieren konnte.

Die Reduktion ist ein wichtiges Hilfsmittel. Nicht nur jetzt, sondern – wie gesagt – auch für die Reduktion in den Komplexitätsklassen \(P\), \(NP\), usw. Dazu aber in den nächsten Beiträgen mehr.

Was können wir derweil damit tun?

Beispiel: Reduktion des spezielle Halteproblem auf das allgemeinen Halteproblems

Ist doch ein nettes Beispiel für eine Reduktion, oder?

Formal suchen wir daher eine totale Funktion \(f:\mathbb{N}\rightarrow\mathbb{N}^2\), die unser spezielles Halteproblem auf das allgemeine reduziert. Es muss gelten:

\(B(i)=H(f(i))\)

Erinnerungshilfe: \(B\) ist unsere Maschine (der Barbier), die unser spezielles Halteproblem entscheiden sollte. Und \(H\) die Maschine, die unser allgemeines Halteproblem entscheiden durfte.

Wir definieren nun \(f\) mit

\(f(i)=(i,i)\)

Damit gilt auch: \(B(i)=H(i,i)\) und wir haben damit das spezielle Halteproblem auf das allgemeine reduziert.

Nicht vergessen: die Reduktion ist transitiv, reflexiv aber nicht antisymmetrisch.

Antwort zum Lernziel: Die Reduktion ist ein mächtiges Werkzeug um Probleme auf ein anderes zurückzuführen. Gibt es einen Algorithmus, der das Problem entscheidet, worauf reduziert wurde, so kann auch das reduzierte Problem entschieden werden.

Aber nicht nur für die Berechenbarkeit hat es Auswirkungen, sondern auch auf die Eigenschaften der reduzierten Mengen und ihre Komplemente.  Ist die Menge, auf die reduziert wurde rekursiv oder rekursiv-aufzählbar, so ist die reduzierte Menge ebenfalls rekursiv oder rekursiv-aufzählbar.

War die Reduzierung der Mengen möglich, so ist auch die Reduzierung ihrer Komplemente möglich.

Lernziel 9

Satz von Rice

Kommen wir nun zu einem der wichtigsten Sätze der theoretischen Informatik, den Hr. Gordon Rice im Jahre 1953 aussprach.

Im Skript ist er formal definiert als:

Für jede Menge \(F\subseteq P^{(1)}\)  mit \(F\neq\emptyset\) und \(F\neq P^{(1)}\) ist die Menge \(\varphi^{-1}[F]\) nicht rekursiv/entscheidbar.

In der Wikipedia ist der Satz in einer anderen Form zu lesen.

Zunächst: was ist unser Wunsch? Wir würden gerne wissen, ob eine Funktion eine Eigenschaft hat oder nicht. Was wäre so eine Eigenschaft? Zum Beispiel:

• Programm \(P\) berechnet die Identitätsfunktion
• Die Ausgabe des Programms \(P\) ist maximal \(n\) Zeichen lang
• …

Denkt euch einfach was nicht triviales (was nicht trivial genau bedeutet erkläre ich auch gleich) aus.

Es kann durchaus mehrere Programme (und damit auch mehrere Maschinen) geben, die Funktionen berechnen. Sagen wir einfach mal, wir betrachten

\(F:=\{f\in{P^{(1)}}\mid{f(x)=x}\}\).

Da die Identitätsfunktion berechenbar ist, gibt es eine Programm, die sie berechnet. Sagen wie auch: Es ist das kleinste Programm \(P_f\), das sie berechnet.

Nun konstruieren wir ein weiteres Programm \(P_{f_2}\), das zusätzlich zum Programmcode von \(P_f\) noch eine sinnlose Schleife besitzt, die eine ungenutzte Variable bis \(5\) hochzählt. Offensichtlich berechnet auch \(P_{f_2}\) die Identitätsfunktion. Programm \(P_{f_2}\) ist von \(P_f\) aber verschieden und beide haben auch verschiedene Gödelnummern.

Wir reden aber nicht explizit von Programmen, sondern von den Funktionen, die sie berechnen. Obwohl die Programme \(P_{f}\) und \(P_{f_2}\) verschieden sind, berechnen sie ein und die selbe Funktion: \(f_P=f_{P_2}=Id\). Damit erfüllen sie unsere „Eigenschaft“ \(F\) und wir haben schon mindestens zwei Programme, bzw. ihre Gödelnummern in unserer Menge

\(\varphi^{-1}[F]\) bzw.

\(\{i\mid{\varphi_i\in{F}}\}\)

Was \(\varphi\) ist, wisst Ihr noch? Im Beitrag zur Standardnummerierung hatten wir das bereits. Damit hatten wir alle Funktionen aus \(P^{(1)}\), der Menge der einstelligen, berechenbaren, evtl. partiellen Funktionen nummeriert. Die Gödelnummern \(i\) und \(i_2\) von \(P_{f}\) und \(P_{f_2}\) befinden sich daher in dieser Menge \(\varphi^{-1}[F]\). Und auch noch viele weitere Gödelnummern von Programmen, die unsere Identitätsfunktion \(f(x)=x\) berechnen.

Das Problem ist: diese Menge von Gödelnummern, die die Eigenschaft \(F\) besitzt, ist nach dem Satz von Rice nicht entscheidbar!

Das ist die Kernaussage des Satzes. Nach diesen Erläuterungen können wir die Definition von oben Stück für Stück auseinander nehmen:

Sei \(F\) eine nicht leere (\(F\neq\emptyset\)) echte Teilmenge (\(F\neq P^{(1)}\) und gleichzeitig \(F\subseteq P^{(1)}\)) der Turing-berechenbaren, einstelligen Funktionen. Es ist nicht entscheidbar welche Funktionen, die durch das Programm \(i\) gegeben ist, die Eigenschaft \(F\) hat und welche nicht (\(\varphi^{-1}[F]\) ist nicht rekursiv).

Diese beiden Eigenschaften der Menge \(F=\emptyset\) (es ist die leere Menge) oder \(F=P^{(1)}\) (das ist die komplette Menge der berechenbare, einstelligen Funktionen) werden auch triviale Eigenschaften genannt. Es bedeutet, dass es min. ein Programm geben muss, die diese Funktion berechnet und eines, das sie nicht berechnet.

Wann ist der Satz von Rice also anwendbar? Wenn es um die Eigenschaften von Funktionen (und nicht um die konkreten Maschinen selbst) geht und wenn die Menge der Programme, die diese Funktion berechnen nicht leer ist oder die Klasse der betrachteten Funktionen nicht komplett alle berechenbaren, einstelligen Funktionen umfasst.

Exkurs: Maschine/Programm?!

Warum wird manchmal auch von den Eigenschaften von Turingmaschinen und nicht von Funktionen gesprochen? Erinnert Ihr euch noch an die Church’sche These? Die Klasse der intuitiv berechenbaren Funktionen stimmt der der Klasse der Turing-berechenbaren Funktionen überein.

Damit können alle intuitiv berechenbaren Funktionen von Turingmaschinen berechnet werden und so die Eigenschaften von Funktionen auch die Eigenschaften der Turingmaschinen sein.

Da die Programme, die eine Funktion aus \(P^{(1)}\) berechnen im Endeffekt also bloß Turingmaschinen sind, die die Funktion aus \(P^{(1)}\) berechnen, sind die Gödelnummern der Programme auch die Gödelnummern der zugehörigen Bandmaschinen.

Lasst euch also von den Worten Funktion, Programm, Maschine nicht verwirren 😉

Noch nicht so recht greifbar, oder? Macht nichts. Versuchen wir es mit ein paar Negativbeispielen:

Negativbeispiele

\(F_1=\{i\mid{M_i}\text{ haelt bei der Eingabe von }x\text{ in }5\text{ Schritten }\}\)

\(F_2=\{i\mid{M_i}\text{ hat 20 Zustaende}\}\)

Diese Mengen \(F_1\) und \(F_2\) sind entscheidbar.

In beiden Fällen ist der Satz von Rice nicht anwendbar, da sich die Aussage nicht auf die Funktionen, d.h. die Maschinenmenge, die sie berechnet, sondern auf die konkreten Eigenschaften einer Maschinen bezieht.

Und nun ein paar Positivbeispiele:

Positivbeispiele

\(F_3=\{i\mid{M_i}\text{ haelt nur bei endlich vielen Eingaben}\}\)

\(F_4=\{i\mid{M_i}\text{ berechnet }0\text{ bei Eingabe von }1\}\)

Hier lässt sich der Satz von Rice anwenden.

• Wir prüfen Voraussetzungen \(F\subseteq{P^{(1)}}\) und \(F\neq{P^{(1)}}\):

In \(P^{(1)}\) liegt z.B. \(f(x)=x^2\), damit gilt \(F_3\subseteq{P^{(1)}}\) und \(F_3\neq{P^{(1)}}\).

• Wir prüfen Voraussetzung \(F_3\neq\emptyset\):

Zudem gilt auch \(F_3\neq\emptyset\), denn es gibt min. eine Maschine, die nur bei endlich vielen Eingaben hält, z.B. \(M(x)=1\text{ falls } x<5,\text{ sonst }\perp\). Damit hält Maschine \(M\) nur für \(x<5\).

Die Menge \(F_3\) ist nach Rice somit nicht entscheidbar.

Für \(F_4\) gilt das ebenfalls. Die Prüfung der Voraussetzungen geht analog zu \(F_3\). Auch diese Menge ist nach Rice nicht entscheidbar.

Fazit: Wann können wir den Satz von Rice anwenden? Wenn mindestens eine Maschine (ein Programm) gibt, die die Funktionen aus der zu untersuchenden Menge \(F\) berechnet und es Maschinen (Programme) gibt, die die Funktionen aus \(F\) nicht berechnen.

Genau das ist es, was uns vor Augen führt, dass das Halteproblem unentscheidbar ist. Es ist nämlich eine nicht triviale Eigenschaft und wir können sie nach dem Satz von Rice nicht entscheiden. Damit ist die Menge \(K_{\varphi}^0\) nicht rekursiv/entscheidbar.

Der Satz hat auch weitreichende Folgen im realen Leben. Denn er bedeutet z.B., dass es kein Verifikationswerkzeug in der Softwareentwicklung geben kann, welches alle Programme algorithmisch auf Korrektheit bzgl. ihrer Spezifikation prüft. Es kann welche geben, die bestimmte, ggf. auch alle praktisch relevanten Programme testen können, aber alle? Das geht nach dem Satz von Rice eben nicht.

Aber Achtung: für Teilmengen von \(F\) ist es evtl. möglich, diese zu entscheiden. Daher auch das Beispiel mit der Verifikationssoftware: wir können nicht für jedes Programm entscheiden ob es der Spezifikation entspricht, aber evtl. durchaus für eine Teilmenge davon. Vielleicht ist das gerade die für uns relevante (praxisrelevante) Teilmenge.

Auch wenn die soeben genannte Eigenschaft „Das Programm arbeitet bzgl. seiner Spezifikation korrekt“ bereits praxistauglich ist, so gibt es eine weitere nicht triviale Eigenschaft von Programmen, mit der wir es tagtäglich zu tun haben: die Frage ob ein Programm eine schädliche Funktion hat oder nicht!

Genau diese Fragestellung hat auch weitreichende Folgen für die Antiviren-Hersteller. Aus dem Satz von Rice lässt sich schließen, dass es kein Antiviren-Programm geben kann, dass für alle Programme entscheiden kann ob sie schädlich sind oder nicht.

Antwort zum Lernziel:  Der Satz von Rice hat weitreichende Auswirkungen auf die Praxis. Er besagt, dass nicht triviale Aussagen über eine von einer Turingmaschine berechnete Funktion (ein Programm) nicht entscheidbar sind.

Diese nicht trivialen Aussagen sind Aussagen der Form \(F\neq{P^{(1)}}\) und \(F\neq\emptyset\). Es muss also min. eine Maschine geben, die die Eigenschaft besitzt und min. eine, die sie nicht besitzt.

Um den Satz anwenden zu können, muss man die zu überprüfende Eigenschaft auf diese Voraussetzungen zunächst testen. Werden die Voraussetzungen bzg. der Nicht-Trivialität erfüllt und bezieht sich die Aussage auf eine Funktion und nicht auf die konkrete Maschine, so kann der Satz angewandt werden.

Vielleicht nochmal in anderen Worten (diese habe ich aus irgendeiner Vorlesung, ich weiß aber nicht mehr welcher):

Geben ist eine nicht-triviale Eigenschaft \(F\). Die Menge der Programme, die diese Eigenschaft erfüllen ist unentscheidbar.

Aber Achtung: für eine Teilmenge könnte die Eigenschaft durchaus entscheiden werden, jedoch eben nicht für alle!

Lernziel 7b

Äquivalenz- und Korrektheitsproblem

Kommen wir nun zum Äquivalenz- und Korrektheitsproblem. Das sind beides nicht triviale Eigenschaften von Programmen und damit nicht für alle entscheidbar.

Aber zunächst wieder die Definition, dann die Erklärung:

Es sei \(d:\subseteq \mathbb{N} \rightarrow \mathbb{N}\) definiert durch \(d(i) = div\) für alle \(i \in \mathbb{N}\)

1. Für jedes \(f \in P^{(1)}\setminus \{d\}\) sind die Mengen \(M_f := \{i\mid\varphi_i = f\}\) und \(\mathbb{N}\setminus M_f = \{i\mid\varphi_i \neq f\}\) nicht rekursiv aufzählbar.

2. Die Mengen Äq \(:= \{(i,j)\mid\varphi_i = \varphi_j\}\) und \(\mathbb{N}^2\setminus\) Äq = \(\{(i,j)\mid\varphi_i \neq \varphi_j\}\) nicht rekursiv aufzählbar.

Als erstes haben wir eine Funktion \(d\), welche für jedes Argument divergent ist.

Punkt 1, Korrektheitsproblem: für jede Funktion \(f\) aus den einstelligen, evtl. partiellen, berechenbaren Funktionen \(P^{(1)}\) ohne die überall undefinierten Funktionen \(d\), sind die Mengen \(M_f\), welche aus den Gödelnummern der Programme/Maschinen bestehen, welche die Funktion \(f\) berechnen und der Menge \(\mathbb{N}\setminus M_f = \{i\mid\varphi_i \neq f\}\), der Menge aus den Gödelnummern, welche die Funktion nicht berechnen nicht rekursiv aufzählbar.

Diese Menge ist also nicht einmal semi-entscheidbar, d.h. wir haben keinen Algorithmus, der uns zu einem gegebenen \(f\) für alle \(\varphi_i\) entscheidet ob \(\varphi_i\) die Funktion \(f\) korrekt berechnet. Auch das Komplement davon, die Menge der Programme die die Funktion \(f\) nicht berechnen ist nicht semi-entscheidbar.

In der Praxis würde man das Beispiel aus dem Skript bemühen, wo eine Korrektor ein Testprogramm  entwerfen möchte, welches entscheidet ob ein gegebenes Programm die Funktion \(f\) berechnet.

Punkt 2, Äquivalenzproblem: Die Menge Äq, welche aus Tupel \((i,j)\) der Gödelnummern von Maschinen besteht, welche die gleiche Funktion berechnen (\(\varphi_i=\varphi_j\), sie sind äquivalent zueinander) und der Menge \(\mathbb{N}^2\setminus\)Äq, die aus Tupeln besteht, welche nicht die gleiche Funktion berechnen sind nicht semi-entscheidbar/rekursiv aufzählbar.

Das Äquivalenzproblem kann auf das Halteproblem zurückgeführt werden. Eine Maschine, die uns eine \(1\) ausgibt, wenn zwei Maschinen die gleiche Funktion berechnen, kann uns auch das Halteproblem lösen. Da die Korrektheit und die Äquivalenz eine nichttriviale Eigenschaft eines (oder mehrerer) Maschinen sind, gilt mit dem Satz von Rice (siehe oben), dass man beides nicht entscheiden kann (nur für reguläre Sprachen geht das, aber das wird später noch durchgekaut).

Antwort zum Lernziel: Das Korrektheitsproblem besagt, dass die Menge der Programme, die eine Funktion berechnen nicht einmal semi-entscheidbar ist. Diese Feststellung gilt ebenfalls für die Menge der Programme, welche die gleiche Funktion berechnen (Äquivalenzproblem).

Man kann das Korrektheitsproblem auf das Äquivalenzproblem durch \(f(i)=(i,j)\) reduzieren.

Lernziel 10

Gödel’scher Unvollständigkeitssatz

Der Unvollständigkeitssatz von Gödel besteht aus zwei Teilen (zitiert nach Wikipedia).

Der Erste Unvollständigkeitssatz besagt, dass es in hinreichend starken widerspruchsfreien Systemen immer unbeweisbare Aussagen gibt.

Der Zweite Unvollständigkeitssatz besagt, dass hinreichend starke widerspruchsfreie Systeme ihre eigene Widerspruchsfreiheit nicht beweisen können

Der Teil ist im Skript wirklich gut beschrieben. Es ist einer der wichtigsten Sätze der Logik (Formulierung geklaut aus Wikipedia). Daher würde diesem Lernziel gerne einen eigenen Beitrag widmen.

Also: bitte dort lesen und dann hierher zurück um den Beitrag mit der Antwort zum letzten Lernziel von Kurseinheit 6 abzuschließen 😉

Antwort zum Lernziel: Mit dem Unvollständigkeitssatz kann man sagen, dass nicht jeder mathematische Satz aus den Axiomen formal abgeleitet oder widerlegt werden kann. Kurz gesagt:

Jedes hinreichend mächtige formale System ist entweder widersprüchlich oder unvollständig.

Durch ein Paradoxon können selbst in so einfachen Systemen, wie z.B. Peano, Widersprüche konstruiert und bewiesen werden, so dass es unvollständig bzw. widersprüchlich ist.

Wir haben im Endeffekt also entweder ein widersprüchliches oder ein unvollständiges System (mit letzterem können wir jedoch besser leben).

Und damit haben wie die Kurseinheit 6 auch schon durch. Wer Fehler findet, sofort melden bevor sie sich in den Köpfen einnisten 😉

Buchempfehlung

Update: Index-Fehler zu \(I_1\) (Danke, Martin!)

Update: auch hier habe mich mich noch strikter an die Lernziele gehalten. Zusätzlich dazu wurden noch ein paar Beispiele zu entscheidbaren und semi-entscheidbaren Funktionen eingepflegt um das Verständnis zu erleichtern, was mir hoffentlich gelungen ist 😉

Update 2: ich merke gerade, dass die Einträge zu lang sind. Selbst die Ladezeiten vom Chrome sind bei den Mathe-Symbolen für 10 Seiten exorbitant hoch. Ich habe daher beschlossen die Beiträge daher zu trennen.

Es gibt insg. drei vier Beiträge zur KE6.

• TIA: Rekursive und rekursiv-aufzählbare Mengen (Lernziele KE6, 1/4)
• TIA: Bild- und Projektionssatz (Lernziele KE6 2/4)
• TIA: Halte- Äquivalenz- und Korrektheitsproblem, Reduzierbarkeit, Satz von Rice (Lernziele KE6, 3/4)
• TIA: Gödel’scher Unvollständigkeitssatz (Lernziele KE6, 4/4)

Da die Lernziele im Skript etwas verstreut sind, kann es sein, dass ich etwas springen muss und nicht alles der Reihe nach abhake. Lasst euch davon nicht verwirren.

Dieser Eintrag befasst sich mit rekursiven und rekursiv-aufzählbaren Mengen und ihren Eigenschaften. Wir hatten bereits in den anderen Beiträgen viel mit Mengen zu tun. Ich werde die Erklärungen hier einfach Copy&Pasten, falls sie passen.

Lernziel 1 und 3

Definition rekursiver und rekursiv aufzählbarer Mengen von Zahlen und Wörtern

Zunächst einmal hilft es sich wie Bart bei den Simpsons 100x „Rekursiv = entscheidbar. Rekursiv aufzählbar = Semi entscheidbar“ wahlweise in das Parkett zu kratzen, die Wand zu tapezieren oder sich auf die Stirn tätowieren zu lassen. Nachdem das erledigt ist, wiederholt man das Gleiche dann noch mit der Definition (welche ich aus diesem Beitrag zur Entscheidbarkeit einfach Copy&Paste):

Eine Menge \( T \subseteq M\) ist entscheidbar/rekursiv wenn die charakteristische Funktion \(\chi_T: M \rightarrow \{0,1\}\) definiert durch

\(\chi_T(t)=\begin{cases} 1, & \mbox{ falls } t \in T \\ 0, & \mbox{ sonst}\end{cases}\)

berechenbar ist (Achtung: sie muss berechenbar sein und nicht einfach nur existieren!).

Achtung: die charakteristische Funktion existiert immer und ist im Falle der Entscheidbarkeit auch immer total!

Dann nochmal für r.a.:

Eine Menge \(T\) ist semi-entscheidbar/rekursiv aufzählbar wenn die partielle charakteristische Funktion \(\chi^{‚}_T: M \rightarrow \{1\}\) definiert durch

\(\chi^{‚}_T(t)=\begin{cases} 1, & \mbox{ falls } t \in T \\ \perp, & \mbox{ sonst}\end{cases}\)

berechenbar ist.

Achtung: hier existiert die charakteristische Funktion ebenfalls, sie ist aber nicht mehr total!

Manchmal sagt man auch, dass die „halbe“ charakteristische Funktion berechenbar ist. Oder wie im Skript ausgedrückt:

Eine Menge \(T\subseteq\mathbb{N}^k\) ist semi-entscheidbar/rekursiv aufzählbar wenn es eine partielle berechenbare Funktion \(f:\subseteq\mathbb{N}^k\rightarrow\mathbb{N}\) gibt mit \(T=Def(f)\).

Während sich die Definition für r.a. Mengen über die charakteristische Funktion noch erschließen mag, ist es bei dieser hier ein bisschen abstrakter.

Denkt euch eine Menge \(T\), wo Ihr nur entscheiden könnt ob ein Element zu dieser Menge gehört, aber nicht ob es nicht dazu gehört (sie ist also offensichtlich nur semi-entscheidbar). Und nun lasst Ihr die charakteristische Funktion \(f\) aus der 2. Definition auf jedem Element \(x\) dieser Menge \(A\) laufen.

Gehört das Element \(x\) zu dieser Menge \(T\), so ist die Ausgabe der Funktion \(f(x)=1\). Und das für jedes \(x\in{A}\), dass zur Menge \(T\) gehört. Gehört es nicht zur Menge \(T\), so rechnet die Funktion unendlich lange weiter. Damit sind alle positiv entschiedenen Elemente \(x\in A\) in der Menge \(T\) und ganz \(T\) damit der Definitionsbereich der Funktion \(f\), eben \(T=Def(f)\).

Wenn wir also entscheiden können ob ein Element in einer Menge ist oder nicht, ist die Menge rekursiv (z.B. bei der Entscheidung auf Primzahlen). Können wir nur positive (oder nur negative, aber nie beides) Entscheidungen treffen ob sich das Element in der Menge befindet (z.B. bei dem Halteproblem), dann ist die Menge nur rekursiv aufzählbar. Nicht vergessen: eine rekursive Menge ist auch rekursiv aufzählbar, aber eine rekursiv aufzählbare Menge nicht zwingend rekursiv.

Später kommen wir noch zu ein paar Beispielen für diese Mengen.

Eine weitere, wichtige Eigenschaft für rekursive Funktionen ist die folgende:

Eine unendliche Menge \(A\subseteq\mathbb{N}\) ist rekursiv, gwd. es eine wachsende, totale Funktion \(f\) gibt mit \(A = Bild(f)\). Wachsend bedeutet: \(f(n) < f(n+1)\)

Höre ich euch die Augenbrauen zusammenziehen? Müsst Ihr nicht. Es ist nicht schwer: was eine wachsende Funktion ist, wisst Ihr sicherlich: es ist eine Funktion, dessen Funktionswert bei der Eingabe vom Parameter \(n\) stets kleiner ist als bei der Eingabe von \(n+1\).

Beispiel: \(f(n)=n^2\)

Stellen wir für \(1\leq{n}\leq{5}\) mal die Funktionswerte zusammen:

\(f(1)=1,f(2)=4,f,(3)=9,f(4)=16,f(5)=25\)

Kein Funktionswert von \(f(n+1)\) ist kleiner als \(f(n)\). Damit ist sie wachsend.

Schaffen wir es also so eine Funktion \(f\) anzugeben, wo die Ausgabe (sog. Bildmenge) von \(f\) unsere komplette Menge \(A\) ist, so ist die Menge \(A\) entscheidbar/rekursiv.

Exkurs Nr. 2: weiterhin sind alle endlichen Mengen rekursiv/entscheidbar. Warum? Nehmen wir einfach eine beliebige, endliche Menge \(A\subseteq\mathbb{N}\). Egal welche Eigenschaften wir dieser Menge zuordnen, so können wir (theoretisch) einfach eine riesige charakteristische Funktion angeben, die für jedes Element entscheidet ob es zu \(A\) gehört oder nicht. Denn die Menge ist endlich.

Nun solltet Ihr einen kleinen Eindruck davon bekommen haben was entscheidbar/rekursiv und was semi-entscheidbar/rekursiv-aufzählbar ist.

Exkurs Nr. 3: Zusammenhang zu Wörtern

Der Zusammenhang zwischen Zahlen und Wörtern sollte nach der Standardnummerierung \(\sigma\) der Wörter über \(\Sigma^*\) sollte euch bereits klar sein. Denn alles, was wir über Mengen auf \(\mathbb{N}^k\) oder \(\mathbb{N}\) aufzählen, gilt selbstverständlich auch für Mengen über einem Alphabet \(\Sigma^{*}\).

Mittels Standardnummerierung können wir Worte aus einem Alphabet \(\Sigma\) nummerieren und umgekehrt. Das haben wir im Beitrag über \(\nu_\Sigma\) bereits erfolgreich getan.

Ebenfalls konnten wir Bandprogramme \(BP\) erfolgreich mit \(\nu_P\) nummerieren und entscheiden ob ein Wort über dem „Programmiersprachenalphabet“ \(\Omega^{*}\) ein Bandprogramm ist oder nicht. Damit ist die Menge der Bandprogramme \(BP\), der PASCAL-Programme und die Menge der \(WHILE\)-Programme entscheidbar/rekursiv.

 

Antwort zum Lernziel: eine Menge ist rekursiv/entscheidbar wenn ihre (volle) charakteristische Funktion berechenbar ist. Für eine nur semi-entscheidbare/rekursiv-aufzählbare Menge muss nur die „halbe“ charakteristische Funktion berechenbar sein.

Im ersten Fall können wir damit die vollständige Menge \(A\) entscheiden, d.h. ob ein Element zu dieser gehört oder nicht (formal ausgedrückt: \(x\in{A}\) und \(x\notin{A}\)). Im letzten Fall können wir nur positiv oder negativ entscheiden, aber nie beides gleichzeitig (formal ausgedrückt: \(x\in{A}\) oder \(x\notin{A}\), aber nicht beides gleichzeitig).

Eine Art Ausnahme bildet das Komplement einer semi-entscheidbaren Menge: können wir dieses ebenfalls semi-entscheiden, so ist die komplette Menge entscheidbar. Denn damit haben wir im Endeffekt die positive und negative Antwort, d.h. die „volle“ charakteristische Funktion berechnet.

Lernziel 4

Abschlusseigenschaften rekursiver und rekursiv aufzählbarer Mengen

Im Skript werden die folgenden, abschließenden Eigenschaften von rekursiven/entscheidbaren Mengen genannt:

1. \(A_1, A_2 \subseteq \mathbb{N}^k\) rekursiv. Damit ist auch \(\mathbb{N}^k\setminus A_1, A_1 \cup A_2\) und \(A_1 \cap A_2\) rekursiv.

2. Sei \(A \subseteq \mathbb{N}\) rekursiv, sei \(f \in R^{(1)}\). Dann ist \(f^{-1}[A]\) rekursiv.

3. Sei \(A \subseteq \mathbb{N}^k\), dann gilt: \(A\) rekursiv \(\Longleftrightarrow \pi^{(k)}[A]\) rekursiv.

Die 1. Eigenschaft ist soweit deutlich: \(A_1\) und \(A_2\) sind Teilmengen aus \(\mathbb{N}^k\) mit eben der Stelligkeit \(k\). Restmenge, Vereinigungsmenge und Schnittmenge sind damit auch rekursiv.

Eigenschaft Nr. 2 ist etwas aufwändiger wenn Ihr mit der Schreibweise nicht vertraut seid und (wie ich) Abschnitt 1.3 überlesen habt. Daher hier zur Auffrischung nochmal. Einer Korrespondenz wird eine Funktion \(f\) zugeordnet, die Mengen transformiert. Die Umkehrfunktion davon \(f^{-1}[A]\). Wenn die Menge \(A\) nun rekursiv ist und es eine totale Funktion \(f\) gibt, so ist auch die Umkehrfunktion rekursiv.

Durch die Cantorfunktion aus Eigenschaft Nr. 3 können wir uns bei unseren Untersuchungen auf die rekursiven Teilmengen von \(\mathbb{N}\) beschränken. Wir erinnern uns: wie können mit dieser Funktion \(\pi\) beliebige \(k\)-stellige Tupel auf eine natürliche Zahl aus \(\mathbb{N}\) abbilden. Wer sich nicht dran erinnert, sollte sich nochmal den Beitrag zu Gemüte führen.

Wir haben damit sichergestellt, dass Operatoren die rekursiven Mengen auch wieder in rekursive Mengen transformieren.

Anschließend folgen die Abschlusseigenschaften der rekursiv aufzählbaren/semi-entscheidbaren (r.a.) Mengen:

1. \(A_1, A_2 \subseteq \mathbb{N}^k\) r.a. Damit ist auch \(A_1\cup A_2\) und \(A_1 \cap A_2\) r.a.

2. Sei \(A \subseteq \mathbb{N}\) r.a., sei \(f \in P^{(k)}\). Dann ist \(f^{-1}[A]\) r.a.

3. Sei \(A \subseteq \mathbb{N}^k\), dann gilt: \(A\) r.a. \(\Longleftrightarrow \pi^{(k)}[A]\) r.a.

Die Erläuterung erfolgt analog zu rekursiven Mengen. Bitte aber beachten, dass wir nun auf den partiellen, mehrstelligen, berechenbaren Funktionen \(P^{(k)}\) arbeiten und nicht mehr auf den totalen \(R^{k}\).

Zusammenfassend zitiere ich aus der Wikipedia für die rekursiven/entscheidbaren und rekursiv-aufzählbare/semi-entscheidbare Mengen:

• Jede entscheidbare Menge ist rekursiv aufzählbar, aber es gibt rekursiv aufzählbare Mengen, die nicht entscheidbar sind.
• Eine Menge ist genau dann entscheidbar, wenn sie und ihr Komplement rekursiv aufzählbar sind.
• Jede endliche Menge ist rekursiv aufzählbar.
• Jede rekursiv aufzählbare Menge ist abzählbar, aber nicht alle abzählbaren Mengen sind rekursiv aufzählbar.
• Jede unendliche rekursiv aufzählbare Menge besitzt Teilmengen, die nicht rekursiv aufzählbar sind.
• Der Schnitt von endlich vielen rekursiv aufzählbaren Mengen ist rekursiv aufzählbar; die Vereinigung einer rekursiv aufzählbaren Menge von rekursiv aufzählbaren Mengen ist rekursiv aufzählbar. Es gibt rekursiv aufzählbaren Mengen, deren Komplement nicht rekursiv aufzählbar ist.

Antwort zum Lernziel: die entscheidbaren Mengen sind abgeschlossen bzgl. Komplement, Schnitt und Vereinigung. Die semi-entscheidbaren mengen jedoch nur bzgl. Schnitt und Vereinigung, das Komplement ist nicht semi-entscheidbar (wäre es das, so wäre die Menge vollständig entscheidbar. Siehe vorheriges Lernziel).

Lernziel 2a

Nachweis der Rekursivität/Entscheidbarkeit von Mengen

Was tun wir um die Rekursivität von Mengen zu beweisen? Wir geben ein Flussdiagramm einer verallgemeinerten Registermaschine an, welches die charakteristische Funktion für die zu untersuchende Menge berechnet. Wir entscheiden nun wirklich ob ein Element in der rekursiven Menge ist oder nicht. Dazu verwenden wir alle bereits als berechenbar bewiesenen Funktionen. Mehr nicht.

Hilfreich ist hierfür die Auflistung der berechenbaren Funktionen aus Satz 3.2.5:

• Nullfunktion
• Nachfolger- und Vorgängerfunktion
• Projektion
• konstante Funktion
• Summe
• arithmetische Differenz
• Produkt
• Quotient und Rest
• Exponentation
• Wurzel
• max/min
• Primzahltest und \(x\)-te Primzahl

Könnt ihr alle für euer Flussdiagramm benutzen 😉

Beispiel? Sicher: \(T=\{x\in\mathbb{N}\mid x\text{ ist Primzahl}\}\)

Die dazu notwendige, charakteristische Funktion ist:

\(\chi_T(x)=\begin{cases} 1, & \mbox{ falls } x\text{ Primzahl} \\ 0, & \mbox{ sonst}\end{cases}\)

Test auf Primzahl: Für alle \(y\) mit \(1<y<x\) wird getestet ob es bei der Division von \(x\) durch \(y\) einen Rest gibt. Gibt es bei einem \(y\) keinen Rest, so ist es keine Primzahl (dann ist \(y\) nämlich ein legitimer Teiler von \(x\)).

Damit können wir für jedes \(x\in\mathbb{N}\) entscheiden ob es eine Primzahl ist oder nicht. Das Flussdiagramm für den Test dürft Ihr selbst angeben 😉

Ein weiteres Beispiel wäre z.B. der Test auf die Goldbach-Eigenschaft einer Zahl.

Antwort zum Lernziel: um zu zeigen, dass eine Menge entscheidbar/rekursiv ist, muss die (volle) charakteristische Funktion berechenbar sein.

Dazu gibt man das Flussdiagramm einer verallgemeinerten Maschine (wenn man streng ist, muss man für jeden verallgemeinerten Test seine Berechenbarkeit ebenfalls nachweisen und letztendlich seine Maschine auf die drei Grundoperationen Addition/Subtraktion von \(1\) und Test auf \(0\) zurückführen) an, die diese berechnet und in jedem Fall mit einem Ergebnis hält.

Lernziel 2b

Nachweis der rekursiven Aufzählbarkeit/Semi-entscheidbarkeit von Mengen

Auch hier ist es nicht allzu schwierig. Jede rekursiv aufzählbare (semi entscheidbare) Menge ist auch gleichzeitig aufzählbar und jede aufzählbare Menge ist auch rekursiv aufzählbar (semi entscheidbar). Daher müssen wir es nur schaffen, die Elemente der Menge irgendwie  aufzuzählen. Man macht sich leicht klar, dass der Definitionsbereich und Wertebereich von berechenbaren Funktionen rekursiv aufzählbar ist.

Aber was ist mit \(n\)-Tupeln? Die sind dank Cantor’schen Tupelfunktion auf ein Element reduzierbar, d.h. wir können \(n\)-Tupel auf einelementige Mengen reduzieren und unseren Schabernack mit ihnen treiben.

Wird also gefragt, ob eine Menge rekursiv aufzählbar ist, so geben wir einfach eine charakteristische Funktion an, die die Eigenschaft der Menge nur positiv (oder nur negativ) beantwortet. Für die gegensätzliche Antwort muss unsere charakteristische Funktion (im Gegensatz zur vollen charakteristischen Funktion für entscheidbare Mengen) nicht halten, Hauptsache sie sagt uns zuverlässig eine der beiden Antworten. Ein gutes Beispiel ist das Post’sche Korrespondenzproblem.

Beispiel: Post’sches Korrespondenzproblem

Das Post’sche Korrespondenzproblem beschreibt das Problem bei Wortpaaren \((x_1,y_1),…,(x_n,y_n)\) eine Folge \(i_1,…,i_k\) mit der Eigenschaft: \(x_{i_1}x_{i_2}…x_{i_k} = y_{i_1}y_{i_2}…y_{i_k}\) zu finden. Ist natürlich wieder etwas abstrakt, aber probieren wir das mal an einem Beispielproblem:

Beispielproblem \(P=((01,1),(0,000),(01000,01))\)

\(P\) nennt man Problemfall oder Instanz.

Fragestellung: gibt es eine Lösung (d.h. eine Folge von Indices) \(I\) zum Problemfall \(P\)? Wenn ja, ist die Folge eine Lösung von \(P\).

Wir müssen hier also eine Kombination von zwei Wortkombinationen \(\omega_1 = \omega_2\) finden und die folgenden Regeln einhalten:

• \(\omega_1\) darf nur aus den 1. Elementen der 3 Wortpaare bestehen: \(01,0\) und \(01000\).
• Das Wort \(\omega_2\) darf nur aus den 2. Elementen der 3 Wortpaare bestehen: \(1,000\) und \(01\).
• Die Wortkombinationen \(\omega_1\) und \(\omega_2\) dürfen beliebig lang sein.

Was Indices sind, ist euch klar? Nein, keine Sorge. Kommt gleich. Es liegt also an unserer Kombinationsgabe eine passende Index-Kombination zu finden, so dass am Ende gilt: \(\omega_1=\omega_2\).

Eine mögliche Lösung wäre \(\omega_1 = 01000\mid{0}\mid{0}\mid{01}\) und \(\omega_2=01\mid{000}\mid{000}\mid{1}\). (die \(\mid\) sind nur optische Trennzeichen damit Ihr die Elemente identifizieren könnt aus denen die Worte bestehen).

Die zugehörigen Indices wären: \(I_1=(3,2,2,1)\). Damit ist \(I_1\) eine Lösung für \(P\) und \(P\) damit gelöst.

Die Indices sind nichts weiter als die Nummer des Tupels, dass zur Bildung herangezogen wird. Da wir für das erste Wort \(\omega_1\) nur die ersten und für das zweite Wort \(\omega_2\) nur die zweiten Elemente aus den Tupeln benutzen dürfen, reicht uns als Angabe einfach nur die Nummer des Tupels.

Würden wir z.B. die folgende Lösung austesten wollen: \(I_2=(2,3,1,1)\), so wären die Worte \(\omega_1\) und \(\omega_2\):

\(\omega_1=0\mid{01000}\mid{01}\mid{01}\) und

\(\omega_2=000\mid{01}\mid{1}\mid{1}\)

Da \(\omega_1\neq\omega_2\), ist die mögliche Lösung \(I_2\) falsch und \(P\) noch nicht gelöst. Aber was nicht ist, kann ja noch werden!

Um zu zeigen, dass die Menge dieser Worttupel rekursiv aufzählbar/semi entscheidbar ist brauchen wir nur zu zeigen, dass die Menge der Definitionsbereich einer partiellen Funktion ist und die dazugehörige Maschine anzugeben, welche die charakteristische Funktion für diese Menge berechnet und in jedem Fall mit einer \(1\) terminiert wenn das Element in der Menge ist oder nicht terminiert, wenn es das nicht ist.

Die charakteristische Funktion für dieses Problem wäre:

\(\chi^{‚}_P(I)=\begin{cases} 1, & \mbox{ falls }\omega_1=\omega_2 \\ \perp, & \mbox{ sonst}\end{cases}\)

Das Flussdiagramm beschreibe ich hier ebenfalls am besten in Pseudocode:

1. Setze \(n=1\)
2. Fange mit einer Indexfolge \(I\) der Länge \(n\) an
3. Erstelle durch den Index \(I\) die Worte \(\omega_1\) und \(\omega_2\) mit Länge \(n\)
4. Prüfe ob \(\omega_1=\omega_2\).

   Wenn ja, so ist eine Lösung für \(P\) gefunden: HALT!

   Wenn nein, setze \(n=n+1\) und gehe zu Punkt 2.

Wie man am Pseudocode gut erkennen kann, kann man zu einer gegebenen Probleminstanz \(P\) eine Lösung durch systematisches ausprobieren finden.

Es ist damit sichergestellt, dass wir so tatsächlich eine korrekte Lösung finden wenn es eine gibt. Und wenn nicht? Da die Länge der Indexfolge unendlich ist und unsere Worte somit unendlich lang werden, kann es sein, dass wir niemals anhalten. Im ungünstigsten Fall läuft unser Programm für eine Kombination also ewig.

So können wir nur schlussfolgern ob eine konkrete Belegung von \(I\) eine Lösung darstellt oder nicht. Aber wir werden nie wissen ob \(P\) nicht doch vielleicht eine Lösung hat.

Kleiner Exkurs: Tatsächlich können wir das Problem für eine kleine Anzahl an Paaren wirklich entscheiden (für ein oder zwei Paare ist das Problem nach Ehrenfeucht und Rozenberg (1981) entscheidbar)! Für die Anzahl zwischen zwei und drei Paaren ist es noch nicht ganz geklärt, während die Anzahl von sieben paaren bereits ausreicht um von Unentscheidbarkeit zu sprechen (Matiyasevich, 1996).

Noch ein Exkurs: Eine weitere Möglichkeit zu zeigen, dass das Post’sche Korrespondenzproblem nicht entscheidbar ist die Reduktion einer nicht entscheidbaren Menge auf dieses. Aber zum Thema Reduktion kommen wir noch in Teil B der theoretischen Informatik.

Antwort zum Lernziel: Um zu zeigen, dass eine Menge semi-entscheidbar/rekursiv-aufzählbar ist, muss die „halbe“ charakteristische Funktion berechenbar sein. Wir müssen also mit Gewissheit sagen können, ob ein Element zur Menge gehört. Das Gegenteil ist uns hier aber vergönnt und wir nehmen es in Kauf, dass unsere Testmaschine für eine Eingabe im ungünstigsten Fall ewig rechnet.

Dazu gibt muss man ebenfalls man das Flussdiagramm einer verallgemeinerten Maschine angeben, aus der ersichtlich ist, dass sie eine Eingabe in jedem Fall positiv bewertet wenn es denn eine Lösung zum gestellten Problem ist und so lange weiterrechnet bis eine Lösung gefunden ist. Im schlimmsten Fall eben ewig.

Lernziel 6

Erläuterung des Zusammenhangs zwischen rekursiven und rekursiv-aufzählbaren Mengen

Eine spannende, aber offensichtliche Beziehung zwischen entscheidbaren und semi-entscheidbaren Mengen ist: eine Menge ist entscheidbar wenn die Menge selbst und ihr Komplement semi-entscheidbar sind. Formal ausgedrückt:

Eine Menge \(A \subseteq \mathbb{N}^k\) ist rekursiv, gdw. \(A\) und \(\mathbb{N}^k\setminus A\) r.a. sind.

Nehmen wir also an, wir haben eine semi-entscheidbare Menge \(A\subseteq\mathbb{N}\). Wie wir wissen, ist sie semi-entscheidbar, d.h. wir können entscheiden ob ein Element zu dieser Menge gehört. Aber nicht das Gegenteil.

Und was wäre dann die Menge \(\mathbb{N}\setminus{A}\)? In dieser Menge wären genau die Elemente, die zwar aus \(\mathbb{N}\) sind, sich aber nicht in \(A\) befinden.

Im Endeffekt haben wir so quasi zwei „halbe“ charakteristische Funktionen, die jeweils einen Teil entscheiden, welchen die andere charakteristische Funktion nicht entschieden hat. Beide zusammen bilden dann eine „volle“ charakteristische Funktion für \(A\).

Beispiel: \(A\subseteq{B}\)

Wir können also die Menge \(A=\{a,b,c,d,e\}\) semi-entscheiden. Ob ein Element nicht in der Menge \(A\) ist hingegen nicht.

Und was wäre wenn wir das Komplement \({B\setminus{A}}\) entscheiden könnten? Also nur die Elemente \({B\setminus{A}}=\{f,g,h,i,j\}\)? Dann könnten wir für alle Elemente aus \(A\) sagen, ob sie zu Menge \(A\) gehören und für den Rest bestimmen ob sie zu \({B\setminus{A}}\) gehören. Damit würde für jedes Element eine positive und negative Entscheidung gefällt werden könne.

Und wenn das der Fall ist, ist \(A\) was? Genau! Komplett entscheidbar/rekursiv.

Die charakteristische Funktion \(cf_A\) für \(A\) wäre also:

\(\chi_A(x)=\begin{cases} 1, & \mbox{ falls } x \in A \\ 0, & \mbox{ wenn } x\in B\end{cases}\)

Fertig. Damit ist die Menge \(A\) (und natürlich auch \(B\)) rekursiv/entscheidbar.

Antwort zum Lernziel: Ist es uns möglich die Teilmenge einer anderen Menge \(A\subseteq{B}\) positiv (aber nicht negativ) zu entscheiden, so ist diese semi-entscheidbar. Können wir für den Rest, d.h. die Menge ohne die bereits positiv entschiedene Menge \(B\setminus A\) ebenfalls entscheiden, so ist die gesamte Menge \(A\) damit rekursiv/entscheidbar.

Weiter geht es mit den nächsten Lernzielen im Beitrag zum Bild- und Projektionssatz.

Bei Fehlern gilt wie immer: ASAP in die Kommentare damit.