Theoretische Informatik – Seite 11 – Informatik an der Fernuni

7. April 201325. November 2025

TIB: Maschinenmodelle und Komplexitätsklassen (Lernziele KE1, Update 4)

Update 6: Große Fehlerkorrektur. Finde ich super, dass Ihr euch die Mühe macht, die Fehler aufzuschreiben. Das hilft dem nachfolgenden Leser ungemein! Danke Walter.

Update 5: Fehlende Marke 4 im Flussdiagramm hinzugefügt. Die Berechnung musste daher geringfügig geändert werden (Danke, Alex).

Update 4: Tippfehler beseitigt in Lernziel 3 nach Kommentar von Carina.

Update 3: Nach dem Einwand von Philipp habe ich das Flussdiagramm abgeändert. Im Skript wird als Ausgabeband 0 verwendet, Band 1 ist das Eingabeband und der Rest sind Arbeitsbänder. Ich habe mich hier nicht so ganz daran gehalten, da es für das Beispiel unwesentlich ist.

Ist aber natürlich nicht schön wenn ich mich nah am Skript bewegen und Details vernachlässige, die das Verständnis erschweren. Daher: Danke für das aufmerksame Lesen 😉 Band 0 ist nun das Ausgabeband.

Update: Mittlerweile ist KE7 von TIA bereits fertig.

Update: Hier habe ich bei der Überarbeitung einige Fehler entfernt, die evtl. zu Verständnisproblemen geführt hätten.

Lernziel 1

Definition der Komplexitätsmaße Zeit und Band für Turing-Maschinen

Bevor wir die Komplexitätsmaße definieren können, müssen wir zunächst wissen was Komplexität ist. Hierzu ist im Skript ein schönes Beispiel gegeben: mit der Schrittzahlfunktion haben wir die Güte einer Maschine, bzw. eines konkreten Programms. Wir haben jedoch ein gesteigertes Interesse an der Komplexität des effizientesten Programms für einen Algorithmus. D.h. wir suchen obere (jede Schranke, die über der Schranke eines bereits bekannten Programms für unseren Algorithmus liegt) und untere Schranken (die minimalste Schranke für alle Programme zu unserem Algorithmus).

Zusätzlich dazu wird im Skript der Begriff Sprache definiert:

Sei $M$ eine $TM$ über dem Ein-/Ausgabealphaber $\Sigma$. Dann ist

$L_M := \{x\in\Sigma^{*}\mid f_M(x) = \varepsilon\}$ die von $M$ erkannte Sprache.

Ist $f_M$ total, so sagen wir: $M$ entscheidet die Sprache $L_M$.

Wie wir wissen beinhaltet $\Sigma^{*}$ alle Wörter über dem Eingabealphabet $\Sigma$. Hält die Maschine $TM$ in einem Endzustand wenn ein Wort $x$ aus $\Sigma^{*}$ in diese eingegeben wird, so wird das Wort $x$ von der Maschine $TM$ akzeptiert. Alle von $TM$ akzeptierten Worte aus $\Sigma^{*}$ werden die von $TM$ akzeptierte Sprache $L_M$ genannt.

Erkannte/Akzeptierte Sprachen sind die rekursiv aufzählbaren Sprachen, d.h. sie terminieren ggf. nicht für jede aber in jedem Fall für jede akzeptierte Eingabe. Wir haben also eine Positiv- oder Negativentscheidung für eine akzeptierte Eingabe (aber nicht beides). D. h. die Maschine hält nur bei akzeptierten Eingaben. Bei anderen Eingaben läuft sie ewig weiter. Das Problem dabei ist, dass wir letztendlich nicht wissen, ob eine Eingabe nun tatsächlich erkannt / akzeptiert wird. Evtl. rechnet die Maschine ja noch für die Eingabe…

Die entscheidbaren Sprachen – also bei den Eingaben, wo die Maschine in jedem Fall mit einer Positiv- oder Negativentscheidung terminiert, $f_M$ ist als überall definiert, d.h. total – nennen wir rekursiv. Hier haben wir für jede Eingabe (irgendwann) einen finalen Zustand der Maschine, der uns für eine EIngabe $X$ die Entscheidung mitteilt.

Was sind aber nun Komplexitätsmaße Zeit/Band für $TM$? Eine $TM$ ist ein abstraktes Modell eines Rechners. Mit der Schrittzahlfunktion $t_M$ haben wir unsere Rechenzeit für die Maschine $M$, d.h. $t_M$ ist unsere Zeitkomplexität. Der Bandbedarf ist unser $s_M$, d.h. unsere Bandkomplexität. Sie gibt an wie viele der Felder beim erreichen der Endkonfiguration (d.h. das Ergebnis steht auf dem Ausgabeband) auf den Arbeitsbändern benutzt wurden. Durch die im Skript gemachten Einschränkungen des Befehlssatzes (Ein- und Ausgabeband kann nicht als Arbeitsband missbraucht werden) für die Maschine, brauchen Ein- und Ausgabeband nicht in die Berechnung einbezogen zu werden. Versuchen wir es an einem einfachen Beispiel zur Verdeutlichung.

Beispiel für Band- und Zeitkomplexität

Wir nehmen eine simple Maschine $M$, die uns $f(n) := n+1$ ausgibt.

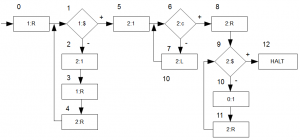
Funktionsweise: die Maschine tut nichts anderes als die Eingabe von Band 1 (Eingabeband) auf Band 2 (Arbeitsband) zu schreiben, eine 1 hinzuzufügen, dann den Lesekopf wieder an den Anfang von Band 2 zu setzen und seinen Inhalt auf Band 0 (Ausgabeband) zu schreiben. Beachtet: $c$ ist das Anfangs- und $\\$$ das Endzeichen. So können wir auf den Bändern von Wortanfang bis Wortende navigieren. Nachdem wir ein Zeichen auf ein Band geschrieben haben müssen wir den Schreibkopf auf Band $0$ auch nicht eine Stelle weiter rücken, da wir im Skript die $TM$ dahingehend erweitert haben, dass das automatisch passiert.

Analysieren wir zunächst die Zeit und nehmen als Eingabe ein $n=2=11$. Nehmt euch am besten Stift und Paper und spielt die Maschine nach. Wir gehen davon aus, dass sich der Lesekopf zu Beginn auf Band 0 bei $c$ befindet, bei Band 1 und 2 jedoch direkt auf dem ersten leeren Feld nach dem Anfangszeichen $c$. Am Ende sollten die Folge der besuchten Marken so aussehen:

0,1,2,3,4,1,2,3,4,1,5,6,7,6,7,6,7,6,8,9,10,11,9,10,11,9,10,11,9,12.

Wenn ich mich nicht verzählt habe sind es genau 30 besuchte Marken.

Fangen wir also mit der Abschätzung an:

Marke 0 wird immer 1x besucht (1)
Marken 1, 2, 3 und 4 werden genau $2$ mal besucht und zum Abschluss noch einmal Marke 1 um dann zu Marke 5 zu kommen $(4*2+1) = 9$
Marke 5 wird immer 1x besucht (1)
Marken 6 und 7 werden $2*(2+1) = 6$ besucht. Wir haben am Ende unseren Lesekopf auf dem Anfangszeichen $c$ bei Band $2$, wo ja am Ende „$c111\\$$“ steht. Also laufen wir insgesamt 3 Mal zurück bis wir wieder auf dem Anfangsmarker $c$ landen. Anschließend wird noch einmal Marke 6 abgefragt und wir kommen auf $7$ Schritte
Marke 8 wird immer 1x besucht (1)
Marken 9, 10, und 11 werden $3*(2+1) = 9$ Mal besucht, da wir uns ja auf dem Band 2 3 Mal nach vorne bewegen müssen um den Endmarker $\\$$ zu erreichen. Dann wird Marke 9 noch einmal abgefragt und wir sind bei $10$ Schritten
Marke 12 ist die Abschlussmarke, welche natürlich nur $1$ Mal besucht wird.

Insgesamt sind wir dann also bei 32 Marken, was unserem manuellen Durchlauf entspricht. Hier sieht man direkt ein, dass die Schleifendurchläufe von der Eingabe $n$ abhängen. Ersetzen wir unsere $2$ nun mit $n$, so kommen wir auf die Gleichung:

$1+4n+1+1+2(n+1)+1+1+3(n+1)+1+1=9n+12$.

Das ist unsere – aufgrund der Einfachheit der Maschine ziemlich genaue – Abschätzung der Zeitkomplexität: $t_M(n) = 9n+12$.

Da uns aber in der Laufzeitberechnung die Konstanten kaum interessieren (sie hängen nicht von der Eingabe, sondern nur von der Rechengeschwindigkeit ab), können wir sie streichen. Für uns spielt nur die Komplexität eine Rolle, die von der Eingabe abhängt (zwar bei beliebigen Rechenleistungen vielleicht schneller ist, aber trotzdem gleiche von der Eingabe abhängige Wachstum hat), so dass die Laufzeit unseres einfachen Programmes in die Komplexitätsklasse $O(n)$ fällt und damit ein lineares Wachstum aufweist.

Was ist aber nun mit der Bandkomplexität? Die ist noch einfacher abzuschätzen. Wie sieht denn die bei der Eingabe von $n$ erreichte Endkonfiguration aus? Die Anfangskonfiguration wäre z. B. bei der Eingabe von $n = 2 = 11$: $(0,(c,c11\$,c))$. Die von da aus erreiche Endkonfiguration wäre: $(12,(c111$,c11$,c111$))$. Da wir uns um das Ein- und Ausgabeband nicht kümmern, sondern nur die Arbeitsbänder (davon haben wir nur eines: Band 2) zählen, landen wir bei einem Speicherplatzverbrauch von $n+1$. $s_M(n) = n+1$, was unsere Bandkomplexität in die selbe Komplexitätsklasse befördert wie unsere Laufzeit: $O(n)$.

Fertig!

Antwort zum Lernziel: bei den Komplexitätsmaßen für Turing-Maschinen unterscheiden wir zwischen Band- und Zeitkomplexität. Ersteres ist der Bandverbrauch, der mit $s_M(n)$ bezeichnet wird und die Auslastung der Arbeitsbänder (Eingabe- und Ausgabeband begutachten wir nicht) angibt. Letzteres ist $t_M(n)$ und gibt die Anzahl der Schritte an, die bei der Eingabe von $n$ zur Endkonfiguration führt.

Lernziel 2

Definition der Komplxitätsklassen

Damit sind wir auch schon bei den Klassen angekommen. Oben haben wir die konkrete Komplexität einer Maschine berechnet. Aber was ist wenn wir noch ein paar unsinnige Schleifen in die obige Maschine einbauen, die von der Eingabe $n$ abhängen ? Wir könnten die Berechnung der simplen Funktion $f(n) = n+1$ durch diese Schleifen dann so verlangsamen, dass die Berechnung erst in exponentieller Zeit abgeschlossen wäre. Selbst wenn es totaler Unfug ist.

Ihr ahnt es wahrscheinlich schon: wir haben keinerlei Interesse an der Komplexität einer konkreten Maschine, die unsere Funktion berechnet. Denn davon kann es viele geben. Für uns ist diese Aussage nur in Bezug auf die Funktion selbst spannend: wie komplex (schnell) ist der schnellste Algorithmus, der unsere Funktion berechnet?

Ein Beispiel gefällig? Gerne: Rucksack-Problem

Eine rekursive Implementierung des Algorithmus hat eine Zeitkomplexität aus der Klasse $O(m^n)$ (polynomielles Wachstum) und den Speicherplatzverbrauch von $O(n)$ (lineares Wachstum). Mittels dynamische Programmierung ist es jedoch möglich die Laufzeit auf $O(m*n)$ zu drücken (hierzu bitte den Wikipedia-Artikel studieren, ggf. schreibe ich später auch mal was dazu). Zunächst hatte also unsere Funktion $f_{Rucksack}$ die Komplexität $O(m^n)$. Dann haben wir es geschafft einen Algorithmus (anhand einer Maschine) zu entwerfen, die unsere Funktion $f_{Rucksack}$ in die Komplexitätsklasse $O(m*n)$ brachte. Und wenn wir keinen anderen, effizienteren Algorithmus finden, bleibt sie auch erstmal dort.

Ist nun klar warum wir uns für die maximale/minimale Komplexität der Algorithmen und nicht konkreter Maschinen interessieren?

Antwort zum Lernziel: die Komplexitätsklassen geben an, welche obere Schranke für einen Algorithmus zu erwarten ist und nicht von der konkreten Maschine, vom der der Algorithmus umgesetzt wird. Es interessiert uns also nur der Worst Case. Dieser wird mittels Landau-Notation, auch O-Notation genannt ausgedrückt. In den meisten Fällen ist die Zeit- von höherem Interesse als die Bandkomplexität.

Durch diese Abgrenzung können wir eine Hierarchie auf den Komplexitätsklassen bilden.

Lernziel 3

Zusammenhang zwischen Band- und Zeitkomplexität

Das im Skript beschriebene Phänomen ist der Space Time Trade off. In der technischen Informatik durften wir mit Assembler programmieren und konnten so den Speicher- und Rechenzeitverbrauch unserer Programme konkret nachvollziehen. Der Zusammenhang müsste den meisten daher klar sein: um Speicherplatz zu sparen kann ich z. B. Schleifen ausschreiben. Der Code wird größer aber das Sprungziel der Schleife muss nicht gespeichert werden. Ebenso ergeht es uns mit komprimierten Daten (angelehnt an den Artikel aus der Wikipedia): wir sparen Speicherplatz, vergeuden aber zum Packen und Entpacken Rechenzeit.

Im Skript sind einige Zusammenhänge zwischen Rechenzeit und Speicherbedarf aufgestellt. Es gibt ein Mindestmaß an Speicherplatz, was ein Algorithmus verbraucht und auch ein Maximum.

$s_M(x) \leq t_M(x) + k$

Da wir Eingabe- und Ausgabeband nicht berücksichtigen ist der Bandbedarf bei der Eingabecodierung festgelegt. Er beträgt die Anzahl der Bänder $k$. Damit ist der Speicherplatzbedarf $S(K_0)$, der Anfangskonfiguration $K_0$ genau gleich $k$. Auch kann er sich in einem Schritt maximal um eines erhöhen, denn wir können ja nur etwas anfügen. Damit sagt der obere Satz nichts weiter aus als: „Der Bandbedarf $s_M$ bei der Eingabe von $x$ ist ${}\leq{}$ der Anzahl der Schritte $t_M$ bei der Eingabe von $x$ plus $k$, eben der Anzahl der Bänder.

$t_M(x) \leq (lg(x)+1)\cdot {c^{s_M(x)+1}}$

„Die Anzahl der Schritte bis zur Endkonfiguration bei der Eingabe von $x$ ist ${}\leq{}$ der Länge der Eingabe + 1 $\cdot {c^{s_M(x)+1}}$„. Wie kommen wir auf $(lg(x)+1)\cdot {c^{s_M(x)+1}}$? Hier müssen wir etwas ausholen:

– $q$ ist die Anzahl der Zustände der Maschine, $g$ die Größe des Arbeitsalphabets + 1. Da wir $q$ Marker haben, haben wir $q$ Zustände.

– Auf dem Eingabeband kann es $lg(x) +2$ Werte für die Kopfposition haben (Länge des Eingabewortes $x$ plus Anfangs- und Endmarker $c$ und $\$$).

– Auf einem Arbeitsband ist die Länge des darauf stehenden Wortes sicher ${}\leq s_M(x)$, d.h. definitiv kleiner/gleich dem kompletten Speicherplatzbedarf am Ende der Berechnung. Damit kann es maximal $s$ Felder auf dem Arbeitsband geben und damit auch $s$ Kopfpositionen. Jedes der Felder kann entweder beschriftet sein oder nicht (wir schauen nach oben: $g$ ist die Größe des Arbeitsalphabets). Diese sind damit durch $s\cdot g^s$ beschränkt.

– Die Möglichkeiten für die Belegung aller Arbeitsbänder ist daher höchstens: ${(s\cdot g^s)}^k$.

Und damit haben wir maximal $q\cdot(lg(x)+2)\cdot{(s\cdot g^s)}^k$ Äquivalenzklassen, was uns zu der obigen Abschätzung bringt: $c := 2q\cdot(2g)^k$.

$t_M(x) \leq c^{s_M(lg(x))}$

Hier muss ich erstmal passen. Der Beweis erschließt sich mir nicht auf Anhieb. Sobald ich die Zusammenfassung von TIA, KE7 fertig habe werde ich hier nochmal reinschauen. Wer jedoch bis dahin den 3. Teil des Zusammenhangs in klaren Worten ausdrücken kann, kann es bitte in die Kommentare schreiben. Ich pflege das dann sofort ein.

Antwort zum Lernziel: der Zusammenhang zwischen Zweit- und Bandkomplexität begründet sich in dem sog. Time-Space-Tradeoff. Häufig gelingt es uns einen Algorithmus schneller ausführen zu können, was jedoch oft zum Nachteil des Speicherplatzverbrauchs geschieht. Anders herum können wir mit einen höheren Speicherplatzverbrauch durchaus Geschwindigkeitsvorteile erzielen.

Ein prominentes Beispiel ist z.B. der Einsatz von Packern, die Daten komprimieren um Speicherplatz zu sparen, aber Rechenzeit aufwenden, da diese Daten wieder entkomprimiert werden müssen.

Auch gibt es Untergrenzen, z.B. für die Geschwindigkeit: um eine Eingabe der Länge $n$ zu lesen, brauchen wir mindestens $n$ Rechenschritte. Ebenso ergeht es uns mit dem Speicherplatz, denn wir können in jedem Schritt nur ein Feld auf dem Band schreiben. D.h. wir können bei $m$ Schritten bis zur Endkonfiguration nicht mehr als $m$ Felder des Bandes beschrieben haben.

Lernziel 4

Darstellung der Aussage der Bandreduktionssätze und Beweisidee

Bei der Normierung werden (ähnlich wie beim Entfernen der Hilfssymbole) die alten Befehle durch Befehlsfolgen ersetzt. Dabei werden auch die Worte wie gehabt verschlüsselt. Ebenso erhöht sich der Bandbedarf (er wird durch die Mächtigkeit des Arbeitsalphabets der ursprünglichen Maschine bestimmt). Ähnlich verhält es sich mit den Arbeitsbändern: wir können durch Erhöhung des Bandbedarfs die Arbeitsbänder auf Eines reduzieren indem wir die Kopfpositionen durch Markierungen auf dem Band (Spuren) simulieren.

Der Zeit- und Bandbedarf der neuen Maschine kann dann abgeschätzt werden durch:

${t_M}^{‚}\leq c\cdot(t_M(x))^2 + c$ ${s_M}^{‚}\leq c\cdot s_M(x) + c$

Eine Effizienzsteigerung im Bereich Zeit erzielt man hier nur noch mit zwei Arbeitsbändern statt nur einem zur Simulation von $k$ Arbeitsbändern

${t_M}^{‚}\leq c\cdot t_M(x)\cdot log\text{ }t_M(x) + c$

${s_M}^{‚}\leq c\cdot s_M(x) + c$

Antwort zum Lernziel: Bei der Normierung einer Turing-Maschine, so dass diese nur ein Arbeitsband hat werden alle anderen Arbeitsbänder auf das einzig verbliebene Arbeitsband codiert. Das geschieht in ähnlicher Weise wie bei den Hilfssymbolen: die Symbole aus dem Arbeitsalphabet werden durch Worte verschlüsselt. Bei den Kopfpositionen arbeiten wir mit $+$ und $–$ auf dem Band. Das bringt uns zur oberen Abschätzung wenn wir nur ein Arbeitsband verwenden.

Verwenden wir zwei Arbeitsbänder können wir zumindest im Bereich Zeit die Effizient erhöhen und kommen so zur unteren Abschätzung. Hier werden zusätzlich Teile der Spuren mit dem zweiten Arbeitsband so verschoben, dass die Kopfmarkierungen auf den versch. Spuren stets an der selben Position sind (im Skript ist dazu kein detaillierter Beweis angegeben).

~~Die Band- und Zeitkomplexität wird durch die Normierung nur durch eine Konstante $c$ erhöht, so dass sie nicht groß ins Gewicht fällt.~~

10. Dezember 201225. November 2025

TIA: Gödel’scher Unvollständigkeitssatz (Lernziele KE6, 4/4)

Update: inhaltlich (noch) nichts, aber als Aufbau zu KE6 entsprechend verwurstelt.

Alle weiteren Beiträge findet Ihr hier:

Zwar sind dem Thema im Skript knapp vier Seiten gewidmet, ich finde aber dieser Satz hat einen eigenen Betrag verdient um nicht in den Lernzielen einfach so unterzugehen. Zunächst: was ist ein Beweissystem? Ein Beweissystem besteht aus Axiomen (Menge von Wörtern) und Schlussregeln, so dass man aus den Axiomen immer neue Wörter (Sätze) ableiten kann.

Ein Beispiel davon ist die Peano Arithmentik. Axiome sind in der Regel selbstverständlich und bedürfen keiner weiteren Begründung. Vor allem in der Peano Arithmetik (PA) sind diese aufgrund ihrer Einfachheit sofort einleuchtend (was diese Arithmetik vor dem 2. Unvollständigkeitssatz von Gödel rettet, aber dazu gleich mehr). Wir können aus diesen unsere Beweise ableiten.

Peano Axiome

Es gibt 5 Peano Axiome, die für sich genommen -wie gesagt- selbstverständlich sind:

1. $1$ ist eine natürliche Zahl

2. Jede natürliche Zahl $n$ hat genau einen Nachfolger $succ(n)$

3. $1$ ist kein Nachfolger einer natürlichen Zahl

4. Die Nachfolger zweier verschiedener natürlicher Zahlen sind verschieden

5. Enthält eine Teilmenge $M \subseteq \mathbb{n}$ die Zahl $1$ und zu jedem Element $n$ auch ihren Nachfolger $succ(n)$, so gilt $M = \mathbb{n}$.

Schlussregeln

Zu den Axiomen benötigen wir auch noch die Schlussregeln. Diese sind:

1. Modus ponens: $A , (A\Rightarrow B) \vdash B$. Wenn aus der Wahrheit von $A$ $B$ folgt und $A$ liegt vor, so gilt auch $B$.

2. Generalisierung: $A \Rightarrow C(x) \vdash A \Rightarrow\forall x_i C(x_i)$. Wenn aus $A$ folgt, dass $C$ für ein beliebiges $x$, dann gilt das auch für alle $x$.

Aus diesen Axiomen und Schlussregeln lassen sich dann Beweise und Operationen ableiten.

Beispiel: Addition $n+1$

Die Addition von $1$ zu einem Wert $n$ ist in der Peano Arithmetik nichts weiter als unsere Nachfolgefunktion: $n+1 = Succ(n)$.

Beispiel: Addition $m+n$, $n=4, m=5$

Auch das können wir uns mit den Peano Axiomen problemlos herleiten, der Ansatz ist aber rekursiver Natur: $(n+Succ(m)) = Succ(n+m)$

$\begin{array}{lcl}4+5&=&Suc(4+4)&\mbox{rekursiv}\\{4+4}&=&Suc(4+3)&\mbox{rekursiv}\\{4+3}&=&Suc(4+2)&\mbox{rekursiv}\\{4+2}&=&Suc(4+1)&\mbox{rekursiv}\\{4+1}&=&Suc(4)&\mbox{dank oben bewiesener Addition von } n+1\\{Suc(4)}&=&5&\mbox{Teilergebnis der letzten rekursion}\end{array}$

Nun setzen wir das rückwärts ein. Denn $4+1 = Suc(4) = 5$. Dass wissen wir ja, da wir das im vorherigen Beispiel bewiesen haben. Also können wir die $4+1$ durch $Suc(4) = 5$ oben in $Suc(4+1)$ ersetzen. Das führen wir dann weiter so fort. Unsere Gleichung sieht am Ende also so aus:

$4+5 = Suc(Suc(Suc(Suc(Suc(4)))))$

Das aufgelöst ergibt offensichtlich (das wollte ich immer schon einmal sagen):

$4+5 = Suc(8) = 9$.

Zusammenhang zum Unvollständigkeitssatz

Nun stellen sich bei so einem Beweissystem ja zwangsläufig folgende Fragen:

1. Widerspruchsfreiheit des Systems: ist es unmöglich einen Widerspruch abzuleiten?

2. Vollständigkeit des Systems: kann jeder wahre Satz der Zahlentheorie abgeleitet werden?

Das damals betrachtete System war die Principia Mathematica von Russel und Whitehead. Hilbert hatte den Wunsch diese beiden Punkte in diesem System zu beweisen. Dass dieser Wunsch nur ein Wunsch bleibt, bewies Hr. Gödel 1931 in seinem Unvollständigkeitssatz, einem der wichtigsten Sätze der Mathematik.

Wir definieren wieder zunächst den Unvollständigkeitssatz wortgetreu aus dem Skript:

1. Kein Beweissystem $V_i$ ist $n$-korrekt und $n$-vollständig.

2. Es gibt eine berechenbare Funktion $h:\subseteq \mathbb{N} \Rightarrow \mathbb{N}$, so dass für jedes $n$-korrekte Beweissystem $V_i$ gilt: $h(i) \notin K_\varphi$ und $„1^{h(i)} \notin K_\varphi“ \notin V_i$.

Was bedeutet $n$-korrekt? $n$-korrekt heißt soviel wie, dass wenn der Satz „Eine Maschine mit der Gödelnummer $1 ^n$ auf sich selbst angewendet hält nicht, die Nummer liegt also nicht in $K_\varphi$“ sich in dem Beweissystem $V_i$ befindet und wahr ist, das auch wirklich stimmt. Die Möglichkeit unwahre Sätze in unserem Beweissystem zu haben, wäre ja nicht unbedingt Sinn der Sache.

Was heißt nun $n$-vollständig? $n$-vollständig bedeutet, dass wenn sich $n$ wirklich nicht in $K_\varphi$ befindet, wir den Satz „Eine Maschine mit der Gödelnummer $1 ^n$ auf sich selbst angewendet hält nicht, die Nummer liegt also nicht in $K_\varphi$“ in unserem Beweissystem haben. Also genau die umgekehrte Richtung.

Dass beides gilt, wäre unsere Wunschvorstellung für unser Beweissystem. Durch die Codierung der Sätze mittels $1^n$ können zudem nun auch unsere Turingmaschinen drauf arbeiten und uns sagen ob sich ein Beweis $\omega$ in einem Satz $v$ unseres Beweissystems wiederfinden kann oder nicht. Man kann somit entscheiden ob ein Wort $\omega$ ein beweis eines Satzes $v$ ist oder nicht.

Damit gibt es auch eine Turing-Maschine, die das entscheiden kann. Die Kontrolle erfolgt rein syntaktisch, da hier die Bedeutung keine Rolle spielt. Formal ausgedrückt wird gefordert:

$U_X := \{(v,w) \in \Sigma^* \times \Sigma^*\mid \omega$ ist ein Beweis für den Satz $v\}$ ist rekursiv.

Damit ist mit dem Projektionssatz die Menge der im System $X$ beweisbaren Sätze $T_X$ rekursiv aufzählbar:

$T_X := \{v \in \Sigma^* \mid (\exists \omega)(v,\omega) \in U_X$\} ist rekursiv aufzählbar.

Was hat uns nun Gödel mit seinem Unvollständigkeitssatz zu dem ganzen Thema genau gesagt? Er hat uns den mathematischen Stinkefinger gezeigt. Ich bringe die umgangssprachliche Formulierung mit der Wortwahl im Skript in Verbindung um es deutlicher zu machen:

1. Jedes Beweissystem ist widersprüchlich oder unvollständig (umgangssprachlich) $\Rightarrow$ Kein Beweissystem $V_i$ ist $n$-korrekt und $n$-vollständig (Skript)

2. Jedes konsistente Beweissystem kann die eigene Konsistenz nicht beweisen (umgangssprachlich) $\Rightarrow$ Es gibt eine berechenbare Funktion $h:\subseteq \mathbb{N} \Rightarrow \mathbb{N}$, so dass für jedes $n$-korrekte Beweissystem $V_i$ gilt: $h(i) \notin K_\varphi$ und $„1^{h(i)} \notin K_\varphi“ \notin V_i$

Wie beweisen wir Punkt 1? Angelehnt an den Artikel aus der Wikipedia zum Thema folgt nun die Skizzierung der Beweise beider Sätze.

Beweisidee zur Widersprüchlichkeit/Unvollständigkeit:

Wenn ein Beweissystem also nicht Widersprüchlich ist (es ist konsistent), dann ist es unvollständig.

Um die Idee nachzuvollziehen, kann man Parallelen zum Paradox des Lügners ziehen. Aber fangen wir mal an:

a) Jedem Satz im System wird eine Gödelnummer zugeordnet, ähnlich unserer Nummerierung in $P^{(1)}$. Diese repräsentiert einen Satz. Aus der Gödelnummer lässt sich auch der Satz wieder ableiten.

b) Konstruktion der Formel $Beweis(x,y)$ (seht Ihr den Zusammenhang mit der oberen Menge $U_x$?). Diese Formel ist dann wahr wenn $x$ die Gödelnummer des Beweises von $S$ ist und $y$ Gödelnummer des Satzes $S$ ist. Damit ist entweder $Beweis(x,y)$ ($x$ ist ein Beweis von $y$) oder seine Negation $\neg(Beweis(x,y))$ ($x$ ist kein Beweis von $y$) wahr.

c) Konstruktion der Formel $Beweisbar(y) = \exists x(Beweis(x,y)$ (es gibt ein $x$, welches ein Beweis von $y$ ist, damit ist $y$ beweisbar). Die Formel „$y$ ist beweisbar“ ist also entweder wahr oder nicht.

d) Anwendung des Diagonallemmas (das arithmetische Konstrukt für die Selbstreferenz) für der Aussage „Ich habe die Eigenschaft F„, wobei man für $F$ die Negation von $Beweisbar(y)$, nämlich $\neg(Beweisbar(y))$ einsetzt. Damit bekommt man die Aussage: „Meine Gödelnummer ist die Gödelnummer einer unbeweisbaren Formel“ bzw. „Ich bin nicht beweisbar„. Das ist der sogenannte Gödelsatz.

Wir sehen schon, wo das hinführt. Nehmen wir an, $y$ sei die gerade konstruierte Aussage „Ich bin nicht beweisbar„. Wenn die Aussage beweisbar wäre, so wäre $Beweisbar(y)$ beweisbar. Gleichzeitig ist die Aussage $Beweisbar(y)$ jedoch auch die Negation von sich selbst. Diese Aussage ist also nicht entscheidbar und das Beweissystem damit oder unvollständig oder widersprüchlich. Widerspruchsfreiheit bedeutet nämlich, dass für einen im System ableitbaren Satz seine Negation nicht ableitbar ist.

Beweisidee zur eigenen Inkonsistenz:

Wenn das Beweissystem konsistent ist, dann ist der Beweis der Konsistenz nicht innerhalb des Systems zu erbringen.

Für den 2. Satz über die Inkonsistenz eines Systems benutzt Gödel seinen ersten Satz und zeigt, dass ein System seine eigene Konsistenz nicht beweisen kann. Das geht wie folgt:

a) da das System lt. dem ersten Unvollständigkeitssatz den Gödelsatz $Gs$ „Ich bin nicht beweisbar“ nicht beweisen kann, ist dieser wahr.

b) daraus lässt sich ableiten: $Konsistent(V) \Rightarrow Gs$. Da dieser Satz aber ebenfalls seine Negation ist, wird das System $V$ dadurch inkonsistent.

Konsistenz schließt Widersprüchlichkeit aus, d.h. wir brauchen ein System, wo wir unser konstruiertes $Beweisbar(y)$ von oben nicht beweisen können. Da $Beweisbar(y)$ ja auch die eigene Negation ist, stecken wir wieder bei seinem Beweis in der Klemme und können die Konsistenz eines Systems (mit den mitteln des Systems) nicht beweisen. Der zweite Unvollständigkeitssatz kann also nur dazu genutzt werden die Widersprüchlichkeit, aber nicht die Widerspruchsfreiheit zu belegen.

Im Endeffekt bedeutet es für uns, dass wir mit den Möglichkeiten eines Systems die Konsistenz dieses Systems nicht darstellen können. Die Frage ist hier: und wozu taugen diese Systeme nun? Wir können mit den Mitteln der Peano Arithmetik (oder eines ausdrucksschwächeren Systems) nicht beweisen, dass die Peano Arithmetik konsistent ist. Obwohl das vielleicht erschreckend klingt, ist es nicht so tragisch wie es sich anhört. Den wir wissen anhand der beiden Sätze, dass die Peano Arithmetik vielleicht unvollständig ist, sie ist aber dennoch durch sich selbst unbewiesen widerspruchsfrei. Warum wird das ohne einen konkreten Beweis akzeptiert? Die Axiome der PA sind zu einfach zu einfach, als dass man sie in Frage stellen könnte.

Das ganze schießt aber nicht aus, dass die Widerspruchsfreiheit eines Systems von einem ausdrucksstärkeren System bewiesen werden könnte. Z.B. würde die Widerspruchsfreiheit von PA innerhalb von ZF-Mengenlehre gezeigt werden können. Was Gerhard Gentzen 1936 auch getan hat, indem er die Hilfe der transfiniten Induktion in Anspruch nahm.

Ein Resultat daraus war, dass man z.B. den Satz von Goodstein in PA zwar formulieren, aber mit den Mitteln der Peano Arithmetik nicht beweisen kann, was Kriby und Paris 1982 zeigten.

Damit haben wir mit der Peano Arithmetik ein widerspruchsfreies, aber unvollständiges System. Womit wir anscheinend ganz gut leben können.

Bei Fehlern: per Mail oder in die Kommentare. Je schneller die aus den Beiträgen raus sind, desto weniger Schaden richten sie evtl. an. Ein Danke auch wieder an die NG vom WS12/13 mit den vielen konstruktiven Beiträgen.

Nun könnt Ihr zurück zum Beitrag 3/4 und die formulierte Antwort zum Lernziel sicher etwas besser nachvollziehen.