Anton – Seite 20 – Informatik an der Fernuni

15. April 201325. November 2025

TIA: Berechenbarkeit auf anderen Mengen (Lernziele KE7, 1/2)

Update: auch diesen Beitrag habe ich auf die Lernziele gemünzt und ein paar Fehler behoben.

Bei dieser KE fühlt es sich leicht an wie ein kleiner Bruch. Es ist ein komplett neues Thema und so erschließt sich auf den ersten Seiten nicht unbedingt der Sinn dahinter. Zumindest mir nicht. Erst gegen Ende der Kurseinheit sieht man, wo die Reise hingegangen ist: zu der Berechenbarkeit der reellen Zahlen. Denn vorher haben wir nur die Berechenbarkeit von Wort- und Zahlenfunktionen betrachtet.

Ich werde daher immer ein Stück vorgreifen wenn ich denke, dass es dem Verständnis förderlich ist und mir nicht die Pointe für den Schluss aufheben.

Lernziel 1

Definition der Berechenbarkeitskonzepte, welche durch eien Nummerierung auf einer Menge $M$induziert werden: $\nu$-rekursiv, $\nu$-r.a, $(\nu,{\nu}^{‚})$-berechenbar

Wir erinnern uns noch an die Churchsche These? Wenn nicht, bitte nochmal nachlesen. Wird hier noch einmal wichtig werden. Im Grunde geht es hier wieder um die Verschlüsselung von Elementen aus abzählbaren Mengen (hier sei nochmal erwähnt: eine Menge ist abzählbar wenn sie die gleiche Mächtigkeit wie $\mathbb{N}$ hat) durch Zahlen oder Wörter, da wir Zahlen mit Register- und Wörter mit Turingmaschinen berechnen können.

Wir erinnern uns auch an unsere Standardnummerierung $\nu_\Sigma$ oder die Nummerierung der einstelligen berechenbaren Zahlenfunktionen $\varphi$. Diese sind total (überall definiert) und sogar bijektiv (bis auf $\varphi$). Nun führen wir ein weiteres Berechenbarkeitskonzept ein, dass nicht weit weg von dem ist, was wir schon haben. Nehmen wir die Definition also Stück für Stück auseinander.

Es seien $\nu: \subseteq \mathbb{N} \rightarrow M$ und $\nu: \subseteq \mathbb{N} \rightarrow M_1$ Nummerierungen.

Eine Menge $X \subseteq M$ heißt $\nu$–rekursiv, gdw. es eine berechenbare Funktion $g: \subseteq \mathbb{N} \rightarrow \mathbb{N}$ gibt mit:
$g(i)=\begin{cases}1&\text{falls } \nu(i) \in X \\0&\text{sonst }\end{cases}$
für alle $i \in Def(\nu)$.

Das ist das Äquivalent zu unserer Entscheidbarkeit/Rekursivität für Zahlen- und Wortfunktionen. Durch die Nummerierung $\nu$ nummerieren wir alle Elemente aus der Menge $M_1$ und die Funktion $g$ entscheidet für uns ob die gegebene Nummer eines Elements aus $M_1$ uns zu einem Element bringt, dass in der Menge $X$ liegt oder nicht.

Es geht uns also im Endeffekt nur darum die Elemente aus der Menge $X$ zu entscheiden.

Machen wir erst einmal weiter im Text. Anschließend folgt ein Beispiel um es etwas „greifbarer“ zu machen.

Eine Menge $X \subseteq M$ heißt $\nu$–rekursiv-aufzählbar, gdw. es eine berechenbare Funktion $g: \subseteq \mathbb{N} \rightarrow \mathbb{N}$ gibt mit:
$g(i)=\begin{cases}existiert&\text{falls } \nu(i) \in X \\div&\text{sonst }\end{cases}$
für alle $i \in Def(\nu)$.

Und hier haben wir das Äquivalent zu unserer Semi-Entscheidbarkeit/rekursiver Aufzählbarkeit.

Wir können zwar immer sagen, ob ein Element zu einer Menge $X$ gehört, haben aber bei der gegenteiligen Aussage ein Problem. Denn hier divergiert die Funktion, sie gibt uns also kein Ergebnis und kann unendlich laufen. Es ist also festgelegt, dass wir im positiven Fall (irgendwann) eine Antwort erhalten, im negativen Fall aber nicht. Prominente Beispiele für die Semi-Entscheidbarkeit sind – wie im verlinkten Beitrag erwähnt – das Halteproblem und der Busy Beaver.

Und nun die letzte Definition für diesen Abschnitt. Hier geht es nicht um eine Menge, sondern um eine Funktion:

Eine Funktion $f \subseteq M_1 \rightarrow M$ heißt $(\nu_1,\nu)$-berechenbar, gdw. es eine berechenbare Funktion $g: \subseteq \mathbb{N} \rightarrow \mathbb{N}$ gibt mit:

$f \circ \nu_1(i) = \nu \circ g(i)$ für alle $i$ mit $\nu_1(i) \in Def(f)$.

Wenn man es ausklammert, hat man vielleicht einen besseren Blick auf die Funktion: $f(\nu_1(i)) = \nu(g(i))$ für alle $i$ mit $\nu_1(i)\in Def(f)$. Okay, das hat nicht unbedingt super geklappt. Diese definition bedeutet, dass eine Menge $(\nu_1,\nu)$-berechenbar ist wenn es ein Verfahren gibt, dass uns zu jeder $\nu_1$-Nummer eines Elements der Definitionsmenge von $f$ eine $\nu$-Nummer der Bildmenge von $f$ berechnet.

Während also die Funktion $f$ auf ihren Mengen (zu einem Definitionswert aus $M_1$ gibt es durch die Funktion einen Funktionswert aus $M$) herumrechnet, kümmern wir uns mit der Funktion $g$ um die Umrechnung der „Nummerierungsnummern“ $\nu$ und $\nu_1$ der beiden Mengen $M_1$ und $M$.

Okay, das ist wahrscheinlich nicht sonderlich einleuchtend. Ich würde sagen, wir suchen uns ein nettes Beispiel.

Was wir zum Durchspielen der Definition brauchen sind

zwei Nummerierungen $\nu$ und $\nu_1$,
zwei Funktionen $f: \subseteq M_1 \rightarrow M$ (diese Funktion nimmt als Argument ein Element aus der Menge $M_1$ entgegen und gibt uns als Ergebnis ein Element aus der Menge $M$) und
$g: \subseteq \mathbb{N} \rightarrow \mathbb{N}$ (diese jedoch bekommt als Argument ein Element aus den natürlichen Zahlen $\mathbb{N}$ und gibt uns auch eins als Ergebnis zurück) und
unsere beiden Mengen $M$ und $M_1$.

Fangen wir einfach mal mit dem Beispiel an und belegen wir unsere Mengen, Funktionen und Nummerierungen mit konkreten Werten:

$M=\{2,4,6\}$: einfach willkürlich gewählt
$M_1=\{1,2,3\}$: ebenfalls willkürlich
$f \subseteq M_1 \rightarrow M: f(x) = 2x$. Willkürlich gewählt. Einzige Bedingung war, dass wir als Definition- und Bildwerte Elemente aus den Mengen $M_1$ und $M$ benutzen müssen. Also habe ich eine Funktion genommen, die Argumente aus $M_1$ auf Ergebnisse aus $M$ abbildet. Ihr könnt einfach mal andere Mengen wählen und die Funktion an diese anpassen. Das Ergebnis ist am Ende gleich.

Wenn wir die Funktion mit unseren Werten aus $M_1$ füttern, so bekommen wir: $f(1) = 2$, $f(2) = 4$ und $f(3) = 6$. Unsere Definitionsmenge $Def(f)$ ist also $\{1,2,3\}$ und entspricht wie gewünscht unserem $M_1$ (die Funktion $f$ ist hier sogar total, denn $Def(f) = M_1$, wie man sieht). Die Bildmenge, unsere Ergebniswerte der Funktion sind $Bild(f) = \{2,4,6\}$ und entsprechen also komplett unserer Menge $M$. Sie ist hier sogar surjektiv (auch rechtstotal genannt), denn $Bild(f) = M$ (jedes Element aus der Menge $M$ wird „getroffen“). Da wir auch noch injektiv (auch linkstotal genannt) sind, ist die Funktion bijektiv. Aber das nur nebenbei.

$g: \subseteq \mathbb{N} \rightarrow \mathbb{N}: g(x) = 2x$. Diese Funktion muss $f \circ \nu_1(i) = \nu \circ g(i)$ für alle $i$ mit $\nu_1(i) \in Def(f)$ erfüllen. Der Kreis $\circ$ ist ja bekanntlich einfach nur eine Komposition. Es muss also gelten: $f (\nu_1(i)) = \nu(g(i))$. Testen wir das doch gleich mit konkreten Werten. Aber vorher müssen wir unsere Nummerierungen wählen:
$\nu: \subseteq \mathbb{N} \rightarrow M$. Die Nummerierung von $M$ ist willkürlich gewählt, aber Hauptsache eindeutig und von $\nu_1$ verschieden. Wir nehmen einfach $-12$ für $\nu$, d.h. $\nu(14) = 2$, $\nu(16) = 4$ und $\nu(18) = 6$. Jetzt noch die Nummerierung der Elemente aus der Menge $M_1$.
$\nu_1: \subseteq \mathbb{N} \rightarrow M_1$. Hier nehmen wir $-6$ für $\nu_1$, d.h. $\nu_1(7) = 1$, $\nu(8) = 2$ und $\nu(9) = 3$. Damit ist auch die Menge $M_1$ nummeriert.

Jetzt können wir mal schauen, ob unsere Funktion $g$ die Bedingung $f \circ \nu_1(i) = \nu \circ g(i)$ erfüllt und probieren alle unsere Werte aus den Mengen $M$ und $M_1$ mal aus:

$\begin{array}{lcl}f(\nu_1(7))&=&f(1)\\{}&=&2\end{array}$

Und nun $g$:

$\begin{array}{lcl}\nu(g(7))&=&\nu(14)\\{}&=&2\end{array}$

Damit ist $f \circ \nu_1(7) = \nu \circ g(7)$ erfüllt. Probiert das doch mal mit den restlichen Werten $8$ und $9$ aus.

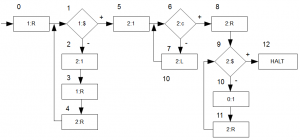
Mit dem Beispiel können wir auch die beiden Grafiken nachvollziehen, die im Skript drin stehen (ich habe beide Diagramme ein Stück weiter unten als Textform inkl. Beispiel beschrieben). Diese durch $f \circ \nu_1(i) = \nu \circ g(i)$ induzierte Beziehung bringt uns zu dem im Skript beschriebenen Ausdruck: Das Diagramm kommutiert.

Eine Funktion $f: \subseteq M_1 \rightarrow M$ ist $(\nu_1,\nu)$-berechenbar wenn es ein Verfahren gibt, welches zu jeder $\nu_1$-Nummer eines Elementes $x \in Def(f)$ eine $\nu$-Nummer von $f(x)$ berechnet.

Am obigen Beispiel angelehnt bedeutet es nichts weiter, dass unsere Funktion $f$ dann $(\nu_1,\nu)$-berechenbar ist wenn wir ein Verfahren zeigen können, dass zu jeder $\nu_1$-Nummer (also $,7,8,9$) eines $x \in Def(f)$ (also $1,2,3$) eine $\nu$-Nummer (also $14,16,18$) von $f(x)$ (also $2,4,6$) berechnet. Um es nochmal in Deutsch zu formulieren: wir müssen ein Verfahren angeben, welches uns zu einer gegebenen Zahl $v_1$-Nummer eine $v$-Nummer ausgibt.

Wählen wir z.B. als $\nu_1$-Nummer wieder die $7$, so müssen wir am Ende eine $14$ als $\nu$-Nummer herausbekommen: $\nu_1(7) = 1, f(1) = 2, \nu(2) = 14$. Anhand der Definitionen können wir so einfach ein Verfahren herleiten: $(2(i-6))+12 = 2i$. Damit bekommen wir zu jeder gegebenen $\nu_1$ eines $x \in Def(f)$ die zugehörige $\nu$-Nummer von $f(x)$. Das haben wir in dem Beispiel getan und gezeigt, dass unsere Funktion $f$ $(\nu_1,\nu)$-berechenbar ist.

Diese beiden Vierecke aus dem Skript sehen in Linie dargestellt wie folgt (inkl. Beispiel) aus:

Diagramm: $\mathbb{N}\rightarrow (g)\rightarrow \mathbb{N}\rightarrow (\nu)\rightarrow{M}\leftarrow (f)\leftarrow M_1\leftarrow (\nu_1)\leftarrow \mathbb{N}$

Beispiel: ${7}\rightarrow g(7)\rightarrow 14\rightarrow \nu(14)\rightarrow{2}\leftarrow f(1)\leftarrow 1\leftarrow \nu_1(7)\leftarrow 7$

Diagramm: $i\rightarrow (g)\rightarrow g(i)\rightarrow (\nu)\rightarrow{f(x)}\leftarrow (f)\leftarrow x\leftarrow (\nu_1)\leftarrow i$

Beispiel: $7\rightarrow g(7)\rightarrow 14\rightarrow \nu(14)\rightarrow{2}\leftarrow f(1)\leftarrow 1\leftarrow \nu_1(7)\leftarrow 7$

Beachtet hier bitte die Einschränkung aus dem Skript. Die Funktion $g$ arbeitet nur vernünftig für alle $i$ mit $\nu_1(i) \in Def(f)$. D.h. Das Ergebnis von $\nu_1(i)$ muss im Definitionsbereich unserer Funktion $f$ liegen. Dieser ist wie wir oben gesehen haben ja $Def(f) = M_1$ und $M_1=\{1,2,3\}$. Also muss das Ergebnis von $\nu_1(i)$ $1,2$ oder $3$ sein. Und das geht nur wenn $i \in \{7,8,9\}$ ist. Für alle anderen Werte für $i$ geht das natürlich nicht.

Antwort zum Lernziel: In den vergangenen Kurseinheiten haben wir uns um die Berechenbarkeit auf Zahlen- und Wortfunktionen gekümmert. In dieser Kurseinheit interessieren wir uns auf die Berechenbarkeitsmodelle auf beliebigen Mengen.

Um jedoch eine Berechenbarkeit auf diesen beliebigen Mengen zu induzieren, denn wir können mittels Register- und Turingmaschinen nur auf Zahlen oder Worten rechnen, brauchen wir Nummerierungen dieser Elemente und angepasste charakteristische Funktionen um unsere Definition für Rekursivität und rekursive Aufzählbarkeit auf diese Mengen zu übertragen.

Wir sind auch nicht nur auf eine einzige Nummerierung beschränkt, die uns Definitions- und Wertemenge nummeriert. Durch eine „Übersetzungsfunktionen“ können wir diese Nummerierungen ineinander „überführen“ und es uns so ermöglichen auf den unterschiedlichen Nummerierungen zweier Mengen rechnen zu können.

Lernziel 2

Nachweis der $\nu$-Rekursivität und $(\nu,{\nu}^{‚})$-Berechenbarkeit

Nun haben wie die $\nu$-Rekursivität, -rekursive-Aufzählbarkeit und $(\nu,{\nu}^{‚})$-Berechenbarkeit definiert, jetzt wollen wir auch etwas mit unserem Wissen anstellen.

Wollen wir doch mal versuchen das für zwei Beispiele aus dem Skript nachzuweisen.

Aufgabe 1: Nachweis der $(id_{\mathbb{N}},\nu)$-Berechenbarkeit einer Nummerierung $\nu: \subseteq \mathbb{N} \rightarrow M$.

Wir machen uns wieder klar, was wir hier zeigen müssen. Wir müssen zeigen, dass es ein Verfahren gibt, welches zu jeder $id_{\mathbb{N}}$-Nummer eines Elementes $x\in Def(\nu)$ eine $\nu$-Nummer von $\nu(x)$ berechnet. Etwas verwirrend, da die Definition noch ein $f$ verlangt, aber das $f$ ist in diesem Fall einfach nur die Nummerierung $\nu$.

Formal ausgedrückt:

$\nu \circ id_{\mathbb{N}}(i) = \nu \circ g(i)$ für alle $i$ mit $id_{\mathbb{N}}(i) \in Def(\nu)$

(nochmal zur Erinnerung $id_{\mathbb{N}}(k) = k$ für alle $k \in \mathbb{N}$, d.h. $id_{\mathbb{N}}(5) = 5$)

Wir suchen also ein $g$, dass die obige Gleichung erfüllt. Wenn Ihr die Komposition klammert sehr Ihr vielleicht auch schon, was für ein $g$ wir suchen:

$\nu (id_{\mathbb{N}}(i)) = \nu(g(i))$ für alle $i$ mit $id_{\mathbb{N}}(i) \in Def(\nu)$

Schon erkannt, was für ein $g$ wir suchen? Wir wählen als Beispiel wieder unsere Nummerierung $\nu$ von oben ($\nu(14) = 2, \nu(16) = 4,\nu(18) = 6$) und haben bei z.B. $i = 14$ folgende Gleichung (zunächst die linke Seite):

$\begin{array}{lcl}\nu (id_{\mathbb{N}}(14))&=&\nu(14)\\{}&=&2\end{array}$

Wir brauchen die Gleichung hier nur aufzulösen:

Wir müssen also $\nu(g(14)) = 2$ setzen. Was nummeriert mit der $2$ unser $\nu(?)=2$? Genau! Die $14$ wird durch $\nu$ mit der $2$ nummeriert (siehe oben): $\nu(14)=2$. Daher muss unser $g$ die $1$ auf die $14$ abbilden: $g(14)=14$ um die Gleichung zu erfüllen.

Aber jetzt habt Ihr sicher schon gemerkt, welches $g$ wir suchen.

Wir wählen $g=id_{\mathbb{N}}$ und rechnen die rechte Seite aus:

$\begin{array}{lcl}\nu (id_{\mathbb{N}}(14))&=&\nu(g(14))\\{}&=&\nu(14)\\{}&=&2\end{array}$

Passt! Damit ist unser $g$ richtig gefunden und es gilt:

$\nu (id_{\mathbb{N}}(i)) = \nu(id_{\mathbb{N}}(i))$

Die Nummerierung $\nu: \subseteq \mathbb{N} \rightarrow M$ ist damit $(id_{\mathbb{N}},\nu)$-berechenbar.

Aufgabe 2: zeigen, dass $\mathbb{Z}^+ := \{z\in\mathbb{Z} \mid z > 0\}$ $\nu_{\mathbb{Z}}$-rekursiv ist

Wir schauen nochmal nach oben auf die Definition der $\nu$-Rekursivität und sehen, dass wir eine Funktion $g$ angeben müssen, die für alle $i \in Def(\nu_{\mathbb{Z}})$ entscheidet ob das Element in $\mathbb{Z}^+$ liegt oder nicht.

Die Definition von $\nu_{\mathbb{Z}}$ ist: $\nu_{\mathbb{Z}} : \mathbb{N} \rightarrow \mathbb{Z}$, $\nu_{\mathbb{Z}}<i,j> := i-j$ $\forall i,j \in \mathbb{N}$.

Noch nicht so ganz klar? Kein Problem: schaut euch nochmal den Beitrag zur Cantorschen Tupelfunktion an, insbesondere die Inverse dazu.

Es gilt $\nu_\mathbb{Z}(500)=<27,4>$. Da $(i-j)>0$ gilt, gilt auch $i>j$. Wir geben nun unsere Funktion $g$ an:

$g<i,j>=\begin{cases}1&\text{falls } i > j \\0&\text{sonst }\end{cases}$

Die Funktion ist berechenbar (Ihr könnt ja mal eine Registermaschine angeben, die sie berechnet) und für alle $k \in \mathbb{N}$ gilt: $\nu_\mathbb{Z}(k) > 0\Longleftrightarrow g(k) = 1$. Die Menge ist also $\nu_\mathbb{Z}$-rekursiv.

Damit hätten wir schon fast die Hälfte abgehakt. Ich hoffe es war alles verständlich. Beitrag 2/2 folgt alsbald.

Und wieder ganz wichtig: wer Fehler findet, bitte sofort in die Kommentare damit niemand auf eine ungenaue Fährte gelockt wird.

Antwort zum Lernziel: Für den Nachweis der $\nu$-Rekursivität einer Menge $X$ muss man eine volle charakteristische Funktion $g$ angeben, die zu der Nummerierung $i$ angibt ob das nummerierte Element $\nu(i)$ in der Menge $X$ liegt oder nicht. Der Nachweis der rekursiven Aufzählbarkeit gelingt durch die „halbe“ charakteristische Funktion.

Für den Nachweis der Berechenbarkeit benötigen wir ein Verfahren, eine Funktion $g$, dass uns die unterschiedlichen Nummerierungen der beiden Mengen „umrechnet“, auf denen die Funktion $f$ eigentlich rechnet (ihre Definitions- und Wertemenge).

Noch ein paar wichtige Definitionen außerhalb der Lernziele, aber nicht weniger wichtig:

Eine weitere, naheliegende Eigenschaft der Nummerierungenen ist auch ihre Transitivität:

Sei $f\subseteq M_1\rightarrow M_2$ $(\nu_1,\nu_2)$-berechenbar und $g\subseteq M_2\rightarrow M_3$ $(\nu_2,\nu_3)$-berechenbar, so ist die Komposition von $g$ und $f$ $g\circ f$ $(\nu_1,\nu_3)$-berechenbar.

Konnte man sich schon fast denken. Braucht sicherlich nicht viele Erklärungen. Man kann direkt sehen, dass wir die Menge $M_2$ als Bindeglied zwischen $f$ und $g$ durch ihre Nummerierung $\nu_2$ haben.

Und nun noch etwas zur Notation:

Eine Notation der Menge $M$ ist eine ggf. partielle, surjektive Funktion $\nu:\subseteq\Sigma^{*}\rightarrow{M}$, wobei $\Sigma$ ein Alphabet ist.

Leuchtet ein. Wir können die Menge $M$ nicht nur nummerieren, wie wir das vorher getan haben und mit Registermaschinen berechnen, sondern wir können diese Menge auch mit Worten über einem Alphabet $\Sigma$ „nummerieren“. Nur nennt man das nicht mehr eine Nummerierung, sondern eine Notation!

Weiter geht es im folgenden Beitrag.

Buchempfehlung

7. April 201325. November 2025

TIB: Maschinenmodelle und Komplexitätsklassen (Lernziele KE1, Update 4)

Update 6: Große Fehlerkorrektur. Finde ich super, dass Ihr euch die Mühe macht, die Fehler aufzuschreiben. Das hilft dem nachfolgenden Leser ungemein! Danke Walter.

Update 5: Fehlende Marke 4 im Flussdiagramm hinzugefügt. Die Berechnung musste daher geringfügig geändert werden (Danke, Alex).

Update 4: Tippfehler beseitigt in Lernziel 3 nach Kommentar von Carina.

Update 3: Nach dem Einwand von Philipp habe ich das Flussdiagramm abgeändert. Im Skript wird als Ausgabeband 0 verwendet, Band 1 ist das Eingabeband und der Rest sind Arbeitsbänder. Ich habe mich hier nicht so ganz daran gehalten, da es für das Beispiel unwesentlich ist.

Ist aber natürlich nicht schön wenn ich mich nah am Skript bewegen und Details vernachlässige, die das Verständnis erschweren. Daher: Danke für das aufmerksame Lesen 😉 Band 0 ist nun das Ausgabeband.

Update: Mittlerweile ist KE7 von TIA bereits fertig.

Update: Hier habe ich bei der Überarbeitung einige Fehler entfernt, die evtl. zu Verständnisproblemen geführt hätten.

Lernziel 1

Definition der Komplexitätsmaße Zeit und Band für Turing-Maschinen

Bevor wir die Komplexitätsmaße definieren können, müssen wir zunächst wissen was Komplexität ist. Hierzu ist im Skript ein schönes Beispiel gegeben: mit der Schrittzahlfunktion haben wir die Güte einer Maschine, bzw. eines konkreten Programms. Wir haben jedoch ein gesteigertes Interesse an der Komplexität des effizientesten Programms für einen Algorithmus. D.h. wir suchen obere (jede Schranke, die über der Schranke eines bereits bekannten Programms für unseren Algorithmus liegt) und untere Schranken (die minimalste Schranke für alle Programme zu unserem Algorithmus).

Zusätzlich dazu wird im Skript der Begriff Sprache definiert:

Sei $M$ eine $TM$ über dem Ein-/Ausgabealphaber $\Sigma$. Dann ist

$L_M := \{x\in\Sigma^{*}\mid f_M(x) = \varepsilon\}$ die von $M$ erkannte Sprache.

Ist $f_M$ total, so sagen wir: $M$ entscheidet die Sprache $L_M$.

Wie wir wissen beinhaltet $\Sigma^{*}$ alle Wörter über dem Eingabealphabet $\Sigma$. Hält die Maschine $TM$ in einem Endzustand wenn ein Wort $x$ aus $\Sigma^{*}$ in diese eingegeben wird, so wird das Wort $x$ von der Maschine $TM$ akzeptiert. Alle von $TM$ akzeptierten Worte aus $\Sigma^{*}$ werden die von $TM$ akzeptierte Sprache $L_M$ genannt.

Erkannte/Akzeptierte Sprachen sind die rekursiv aufzählbaren Sprachen, d.h. sie terminieren ggf. nicht für jede aber in jedem Fall für jede akzeptierte Eingabe. Wir haben also eine Positiv- oder Negativentscheidung für eine akzeptierte Eingabe (aber nicht beides). D. h. die Maschine hält nur bei akzeptierten Eingaben. Bei anderen Eingaben läuft sie ewig weiter. Das Problem dabei ist, dass wir letztendlich nicht wissen, ob eine Eingabe nun tatsächlich erkannt / akzeptiert wird. Evtl. rechnet die Maschine ja noch für die Eingabe…

Die entscheidbaren Sprachen – also bei den Eingaben, wo die Maschine in jedem Fall mit einer Positiv- oder Negativentscheidung terminiert, $f_M$ ist als überall definiert, d.h. total – nennen wir rekursiv. Hier haben wir für jede Eingabe (irgendwann) einen finalen Zustand der Maschine, der uns für eine EIngabe $X$ die Entscheidung mitteilt.

Was sind aber nun Komplexitätsmaße Zeit/Band für $TM$? Eine $TM$ ist ein abstraktes Modell eines Rechners. Mit der Schrittzahlfunktion $t_M$ haben wir unsere Rechenzeit für die Maschine $M$, d.h. $t_M$ ist unsere Zeitkomplexität. Der Bandbedarf ist unser $s_M$, d.h. unsere Bandkomplexität. Sie gibt an wie viele der Felder beim erreichen der Endkonfiguration (d.h. das Ergebnis steht auf dem Ausgabeband) auf den Arbeitsbändern benutzt wurden. Durch die im Skript gemachten Einschränkungen des Befehlssatzes (Ein- und Ausgabeband kann nicht als Arbeitsband missbraucht werden) für die Maschine, brauchen Ein- und Ausgabeband nicht in die Berechnung einbezogen zu werden. Versuchen wir es an einem einfachen Beispiel zur Verdeutlichung.

Beispiel für Band- und Zeitkomplexität

Wir nehmen eine simple Maschine $M$, die uns $f(n) := n+1$ ausgibt.

Funktionsweise: die Maschine tut nichts anderes als die Eingabe von Band 1 (Eingabeband) auf Band 2 (Arbeitsband) zu schreiben, eine 1 hinzuzufügen, dann den Lesekopf wieder an den Anfang von Band 2 zu setzen und seinen Inhalt auf Band 0 (Ausgabeband) zu schreiben. Beachtet: $c$ ist das Anfangs- und $\\$$ das Endzeichen. So können wir auf den Bändern von Wortanfang bis Wortende navigieren. Nachdem wir ein Zeichen auf ein Band geschrieben haben müssen wir den Schreibkopf auf Band $0$ auch nicht eine Stelle weiter rücken, da wir im Skript die $TM$ dahingehend erweitert haben, dass das automatisch passiert.

Analysieren wir zunächst die Zeit und nehmen als Eingabe ein $n=2=11$. Nehmt euch am besten Stift und Paper und spielt die Maschine nach. Wir gehen davon aus, dass sich der Lesekopf zu Beginn auf Band 0 bei $c$ befindet, bei Band 1 und 2 jedoch direkt auf dem ersten leeren Feld nach dem Anfangszeichen $c$. Am Ende sollten die Folge der besuchten Marken so aussehen:

0,1,2,3,4,1,2,3,4,1,5,6,7,6,7,6,7,6,8,9,10,11,9,10,11,9,10,11,9,12.

Wenn ich mich nicht verzählt habe sind es genau 30 besuchte Marken.

Fangen wir also mit der Abschätzung an:

Marke 0 wird immer 1x besucht (1)
Marken 1, 2, 3 und 4 werden genau $2$ mal besucht und zum Abschluss noch einmal Marke 1 um dann zu Marke 5 zu kommen $(4*2+1) = 9$
Marke 5 wird immer 1x besucht (1)
Marken 6 und 7 werden $2*(2+1) = 6$ besucht. Wir haben am Ende unseren Lesekopf auf dem Anfangszeichen $c$ bei Band $2$, wo ja am Ende „$c111\\$$“ steht. Also laufen wir insgesamt 3 Mal zurück bis wir wieder auf dem Anfangsmarker $c$ landen. Anschließend wird noch einmal Marke 6 abgefragt und wir kommen auf $7$ Schritte
Marke 8 wird immer 1x besucht (1)
Marken 9, 10, und 11 werden $3*(2+1) = 9$ Mal besucht, da wir uns ja auf dem Band 2 3 Mal nach vorne bewegen müssen um den Endmarker $\\$$ zu erreichen. Dann wird Marke 9 noch einmal abgefragt und wir sind bei $10$ Schritten
Marke 12 ist die Abschlussmarke, welche natürlich nur $1$ Mal besucht wird.

Insgesamt sind wir dann also bei 32 Marken, was unserem manuellen Durchlauf entspricht. Hier sieht man direkt ein, dass die Schleifendurchläufe von der Eingabe $n$ abhängen. Ersetzen wir unsere $2$ nun mit $n$, so kommen wir auf die Gleichung:

$1+4n+1+1+2(n+1)+1+1+3(n+1)+1+1=9n+12$.

Das ist unsere – aufgrund der Einfachheit der Maschine ziemlich genaue – Abschätzung der Zeitkomplexität: $t_M(n) = 9n+12$.

Da uns aber in der Laufzeitberechnung die Konstanten kaum interessieren (sie hängen nicht von der Eingabe, sondern nur von der Rechengeschwindigkeit ab), können wir sie streichen. Für uns spielt nur die Komplexität eine Rolle, die von der Eingabe abhängt (zwar bei beliebigen Rechenleistungen vielleicht schneller ist, aber trotzdem gleiche von der Eingabe abhängige Wachstum hat), so dass die Laufzeit unseres einfachen Programmes in die Komplexitätsklasse $O(n)$ fällt und damit ein lineares Wachstum aufweist.

Was ist aber nun mit der Bandkomplexität? Die ist noch einfacher abzuschätzen. Wie sieht denn die bei der Eingabe von $n$ erreichte Endkonfiguration aus? Die Anfangskonfiguration wäre z. B. bei der Eingabe von $n = 2 = 11$: $(0,(c,c11\$,c))$. Die von da aus erreiche Endkonfiguration wäre: $(12,(c111$,c11$,c111$))$. Da wir uns um das Ein- und Ausgabeband nicht kümmern, sondern nur die Arbeitsbänder (davon haben wir nur eines: Band 2) zählen, landen wir bei einem Speicherplatzverbrauch von $n+1$. $s_M(n) = n+1$, was unsere Bandkomplexität in die selbe Komplexitätsklasse befördert wie unsere Laufzeit: $O(n)$.

Fertig!

Antwort zum Lernziel: bei den Komplexitätsmaßen für Turing-Maschinen unterscheiden wir zwischen Band- und Zeitkomplexität. Ersteres ist der Bandverbrauch, der mit $s_M(n)$ bezeichnet wird und die Auslastung der Arbeitsbänder (Eingabe- und Ausgabeband begutachten wir nicht) angibt. Letzteres ist $t_M(n)$ und gibt die Anzahl der Schritte an, die bei der Eingabe von $n$ zur Endkonfiguration führt.

Lernziel 2

Definition der Komplxitätsklassen

Damit sind wir auch schon bei den Klassen angekommen. Oben haben wir die konkrete Komplexität einer Maschine berechnet. Aber was ist wenn wir noch ein paar unsinnige Schleifen in die obige Maschine einbauen, die von der Eingabe $n$ abhängen ? Wir könnten die Berechnung der simplen Funktion $f(n) = n+1$ durch diese Schleifen dann so verlangsamen, dass die Berechnung erst in exponentieller Zeit abgeschlossen wäre. Selbst wenn es totaler Unfug ist.

Ihr ahnt es wahrscheinlich schon: wir haben keinerlei Interesse an der Komplexität einer konkreten Maschine, die unsere Funktion berechnet. Denn davon kann es viele geben. Für uns ist diese Aussage nur in Bezug auf die Funktion selbst spannend: wie komplex (schnell) ist der schnellste Algorithmus, der unsere Funktion berechnet?

Ein Beispiel gefällig? Gerne: Rucksack-Problem

Eine rekursive Implementierung des Algorithmus hat eine Zeitkomplexität aus der Klasse $O(m^n)$ (polynomielles Wachstum) und den Speicherplatzverbrauch von $O(n)$ (lineares Wachstum). Mittels dynamische Programmierung ist es jedoch möglich die Laufzeit auf $O(m*n)$ zu drücken (hierzu bitte den Wikipedia-Artikel studieren, ggf. schreibe ich später auch mal was dazu). Zunächst hatte also unsere Funktion $f_{Rucksack}$ die Komplexität $O(m^n)$. Dann haben wir es geschafft einen Algorithmus (anhand einer Maschine) zu entwerfen, die unsere Funktion $f_{Rucksack}$ in die Komplexitätsklasse $O(m*n)$ brachte. Und wenn wir keinen anderen, effizienteren Algorithmus finden, bleibt sie auch erstmal dort.

Ist nun klar warum wir uns für die maximale/minimale Komplexität der Algorithmen und nicht konkreter Maschinen interessieren?

Antwort zum Lernziel: die Komplexitätsklassen geben an, welche obere Schranke für einen Algorithmus zu erwarten ist und nicht von der konkreten Maschine, vom der der Algorithmus umgesetzt wird. Es interessiert uns also nur der Worst Case. Dieser wird mittels Landau-Notation, auch O-Notation genannt ausgedrückt. In den meisten Fällen ist die Zeit- von höherem Interesse als die Bandkomplexität.

Durch diese Abgrenzung können wir eine Hierarchie auf den Komplexitätsklassen bilden.

Lernziel 3

Zusammenhang zwischen Band- und Zeitkomplexität

Das im Skript beschriebene Phänomen ist der Space Time Trade off. In der technischen Informatik durften wir mit Assembler programmieren und konnten so den Speicher- und Rechenzeitverbrauch unserer Programme konkret nachvollziehen. Der Zusammenhang müsste den meisten daher klar sein: um Speicherplatz zu sparen kann ich z. B. Schleifen ausschreiben. Der Code wird größer aber das Sprungziel der Schleife muss nicht gespeichert werden. Ebenso ergeht es uns mit komprimierten Daten (angelehnt an den Artikel aus der Wikipedia): wir sparen Speicherplatz, vergeuden aber zum Packen und Entpacken Rechenzeit.

Im Skript sind einige Zusammenhänge zwischen Rechenzeit und Speicherbedarf aufgestellt. Es gibt ein Mindestmaß an Speicherplatz, was ein Algorithmus verbraucht und auch ein Maximum.

$s_M(x) \leq t_M(x) + k$

Da wir Eingabe- und Ausgabeband nicht berücksichtigen ist der Bandbedarf bei der Eingabecodierung festgelegt. Er beträgt die Anzahl der Bänder $k$. Damit ist der Speicherplatzbedarf $S(K_0)$, der Anfangskonfiguration $K_0$ genau gleich $k$. Auch kann er sich in einem Schritt maximal um eines erhöhen, denn wir können ja nur etwas anfügen. Damit sagt der obere Satz nichts weiter aus als: „Der Bandbedarf $s_M$ bei der Eingabe von $x$ ist ${}\leq{}$ der Anzahl der Schritte $t_M$ bei der Eingabe von $x$ plus $k$, eben der Anzahl der Bänder.

$t_M(x) \leq (lg(x)+1)\cdot {c^{s_M(x)+1}}$

„Die Anzahl der Schritte bis zur Endkonfiguration bei der Eingabe von $x$ ist ${}\leq{}$ der Länge der Eingabe + 1 $\cdot {c^{s_M(x)+1}}$„. Wie kommen wir auf $(lg(x)+1)\cdot {c^{s_M(x)+1}}$? Hier müssen wir etwas ausholen:

– $q$ ist die Anzahl der Zustände der Maschine, $g$ die Größe des Arbeitsalphabets + 1. Da wir $q$ Marker haben, haben wir $q$ Zustände.

– Auf dem Eingabeband kann es $lg(x) +2$ Werte für die Kopfposition haben (Länge des Eingabewortes $x$ plus Anfangs- und Endmarker $c$ und $\$$).

– Auf einem Arbeitsband ist die Länge des darauf stehenden Wortes sicher ${}\leq s_M(x)$, d.h. definitiv kleiner/gleich dem kompletten Speicherplatzbedarf am Ende der Berechnung. Damit kann es maximal $s$ Felder auf dem Arbeitsband geben und damit auch $s$ Kopfpositionen. Jedes der Felder kann entweder beschriftet sein oder nicht (wir schauen nach oben: $g$ ist die Größe des Arbeitsalphabets). Diese sind damit durch $s\cdot g^s$ beschränkt.

– Die Möglichkeiten für die Belegung aller Arbeitsbänder ist daher höchstens: ${(s\cdot g^s)}^k$.

Und damit haben wir maximal $q\cdot(lg(x)+2)\cdot{(s\cdot g^s)}^k$ Äquivalenzklassen, was uns zu der obigen Abschätzung bringt: $c := 2q\cdot(2g)^k$.

$t_M(x) \leq c^{s_M(lg(x))}$

Hier muss ich erstmal passen. Der Beweis erschließt sich mir nicht auf Anhieb. Sobald ich die Zusammenfassung von TIA, KE7 fertig habe werde ich hier nochmal reinschauen. Wer jedoch bis dahin den 3. Teil des Zusammenhangs in klaren Worten ausdrücken kann, kann es bitte in die Kommentare schreiben. Ich pflege das dann sofort ein.

Antwort zum Lernziel: der Zusammenhang zwischen Zweit- und Bandkomplexität begründet sich in dem sog. Time-Space-Tradeoff. Häufig gelingt es uns einen Algorithmus schneller ausführen zu können, was jedoch oft zum Nachteil des Speicherplatzverbrauchs geschieht. Anders herum können wir mit einen höheren Speicherplatzverbrauch durchaus Geschwindigkeitsvorteile erzielen.

Ein prominentes Beispiel ist z.B. der Einsatz von Packern, die Daten komprimieren um Speicherplatz zu sparen, aber Rechenzeit aufwenden, da diese Daten wieder entkomprimiert werden müssen.

Auch gibt es Untergrenzen, z.B. für die Geschwindigkeit: um eine Eingabe der Länge $n$ zu lesen, brauchen wir mindestens $n$ Rechenschritte. Ebenso ergeht es uns mit dem Speicherplatz, denn wir können in jedem Schritt nur ein Feld auf dem Band schreiben. D.h. wir können bei $m$ Schritten bis zur Endkonfiguration nicht mehr als $m$ Felder des Bandes beschrieben haben.

Lernziel 4

Darstellung der Aussage der Bandreduktionssätze und Beweisidee

Bei der Normierung werden (ähnlich wie beim Entfernen der Hilfssymbole) die alten Befehle durch Befehlsfolgen ersetzt. Dabei werden auch die Worte wie gehabt verschlüsselt. Ebenso erhöht sich der Bandbedarf (er wird durch die Mächtigkeit des Arbeitsalphabets der ursprünglichen Maschine bestimmt). Ähnlich verhält es sich mit den Arbeitsbändern: wir können durch Erhöhung des Bandbedarfs die Arbeitsbänder auf Eines reduzieren indem wir die Kopfpositionen durch Markierungen auf dem Band (Spuren) simulieren.

Der Zeit- und Bandbedarf der neuen Maschine kann dann abgeschätzt werden durch:

${t_M}^{‚}\leq c\cdot(t_M(x))^2 + c$ ${s_M}^{‚}\leq c\cdot s_M(x) + c$

Eine Effizienzsteigerung im Bereich Zeit erzielt man hier nur noch mit zwei Arbeitsbändern statt nur einem zur Simulation von $k$ Arbeitsbändern

${t_M}^{‚}\leq c\cdot t_M(x)\cdot log\text{ }t_M(x) + c$

${s_M}^{‚}\leq c\cdot s_M(x) + c$

Antwort zum Lernziel: Bei der Normierung einer Turing-Maschine, so dass diese nur ein Arbeitsband hat werden alle anderen Arbeitsbänder auf das einzig verbliebene Arbeitsband codiert. Das geschieht in ähnlicher Weise wie bei den Hilfssymbolen: die Symbole aus dem Arbeitsalphabet werden durch Worte verschlüsselt. Bei den Kopfpositionen arbeiten wir mit $+$ und $–$ auf dem Band. Das bringt uns zur oberen Abschätzung wenn wir nur ein Arbeitsband verwenden.

Verwenden wir zwei Arbeitsbänder können wir zumindest im Bereich Zeit die Effizient erhöhen und kommen so zur unteren Abschätzung. Hier werden zusätzlich Teile der Spuren mit dem zweiten Arbeitsband so verschoben, dass die Kopfmarkierungen auf den versch. Spuren stets an der selben Position sind (im Skript ist dazu kein detaillierter Beweis angegeben).

~~Die Band- und Zeitkomplexität wird durch die Normierung nur durch eine Konstante $c$ erhöht, so dass sie nicht groß ins Gewicht fällt.~~