Anton – Seite 16 – Informatik an der Fernuni

1. Juni 201325. November 2025

TIB: Endliche Automaten und kontextfreie Grammatiken (Lernziele KE6 2/3), Update 3

Update 3: Korrektur der Beweisidee für Durchschnitt, nicht Vereinigung. Danke Phil.

Update 2: Korrektur Aufgabe aus Lernziel 3. Danke Mike.

Update: Aufgabe mit Lösung hinzugefügt um aus einem Automaten eine Regelmenge abzuleiten.

Ohne viele Worte: weiter in KE6.

Lernziel 3

Wie konstruiert man zu einem endlichen Automaten $A$ einen regulären Ausdruck $\alpha$ mit $L(A)=L(\alpha)$?

Hier kommt einiges an Schreibarbeit auf uns zu. Wie wir aus dem Beitrag zu KE5 wissen, können wir reguläre Sprachen mit einem regulären Ausdruck beschreiben. Um zu beweisen, dass eine Sprache regulär ist, muss man sie auf eine reguläre Grammatik, einen endlichen Automaten, einen regulären Ausdruck oder auf bereits bekannte reguläre Sprachen zurückführen.

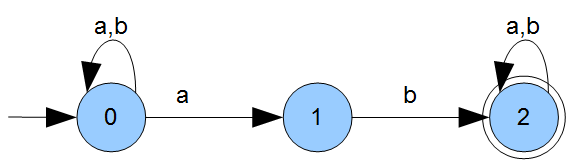
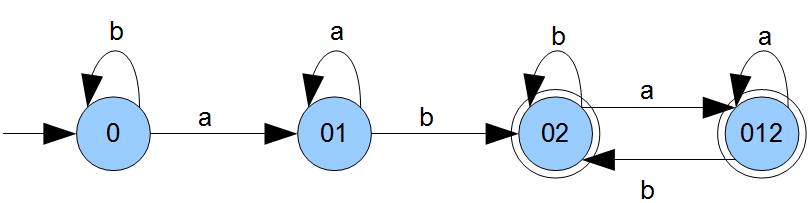
Hier haben wir einen Automaten $A$ zu einer Sprache $L$ bereits gegeben (die Sprache ist also als regulär bewiesen) und suchen nun auch noch einen regulären Ausdruck, der uns dieselbe Sprache beschreibt. Wir verwenden als beispiel wieder den Automaten $A$ aus dem vorherigen Beitrag:

Beispiel: $A=(\{a,b\},\{0,1,2\},0,2,\delta)$ mit

$\delta=\{(1,a,1),(1,b,1),(1,a,2),(2,b,3),(3,a,3),(3,b,3)\}$

Hier nochmal der Graph damit Ihr nicht zwischen den Beiträgen wechseln müsst:

Der Ansatz im Beweis ist ein geringfügig anderer, ich will sagen etwas formaler aus die Vorgehensweise, die ich gleich vorstelle. Das Ergebnis ist aber dasselbe. Wenn jemand eine schöne Erklärung für den formalen Beweis im Skript hat, der die folgenden zwei Formeln verwendet, immer her damit.

${L_{ij}}^{0}=\{a\in\Sigma\mid (i,a,j)\in\delta\}$ ${L_{ij}}^{k}={L_{ij}}^{k-1}\cup{L_{ik}}^{k-1}\cdot({L_{kk}}^{k-1})^*\cdot{L_{kj}}^{k-1}$

Wir machen das etwas weniger formal. Die Schritte sind wie folgt:

Wir führen einen neuen Startzustand $S$ ein, der mit einem leeren Wort $\epsilon$ bereits in unseren ehemaligen Startzustand übergeht. Ebenfalls wird ein neuer Endzustand $E$ eingesetzt, zu dem ein Pfeil von jedem ehemaligen Endzustand gezogen wird. Auch hier wird das leere Wort als Übergang verwendet. Unser neuer Graph sieht wie folgt aus:

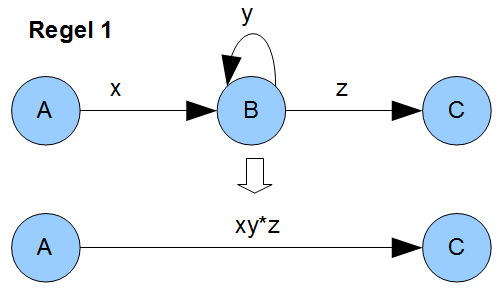
Wenn wir uns den Übergang von Zustand $0$ zu Zustand $1$ anschauen, fällt auf, dass wir in jedem Fall ein $a$ als Abschluss der Zeichenkette brauchen um zu Zustand $1$ zu kommen. Beliebig lange Worte, die aus $a$ oder $b$ zusammengesetzt sind, spielen für den Übergang aufgrund der Schleife im Zustand $0$ keine Rolle solange das $a$ als Suffix im Wort vorhanden ist. Das führt uns auch zu den beiden Überführungsregeln, die wir brauchen. Ein Bild sagt mehr als tausend Worte:

Klammern wir die Ausdrücke bei Regel 1, wird es evtl. deutlicher: $\{x\}\cdot\{y\}^*\cdot\{z\}$ ist dann der gesuchte, reguläre Ausdruck um von Zustand $A$ zu Zustand $C$ zu kommen nachdem man Zustand $B$ entfernt hat. Ein Wort, dass den regulären Ausdruck erfüllen würde, wäre z.B. $xyyyyyyyz$ oder $xz$. Eines, dass ihn nicht erfüllt ist $xy$.

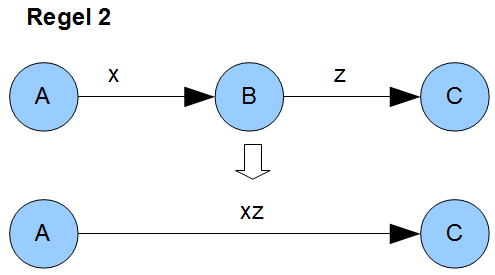
Regel 2 ist noch einfacher: Von Zustand $A$ zu Zustand $C$ kommt man durch die Konkatenation von $x$ und $z$. That’s it.

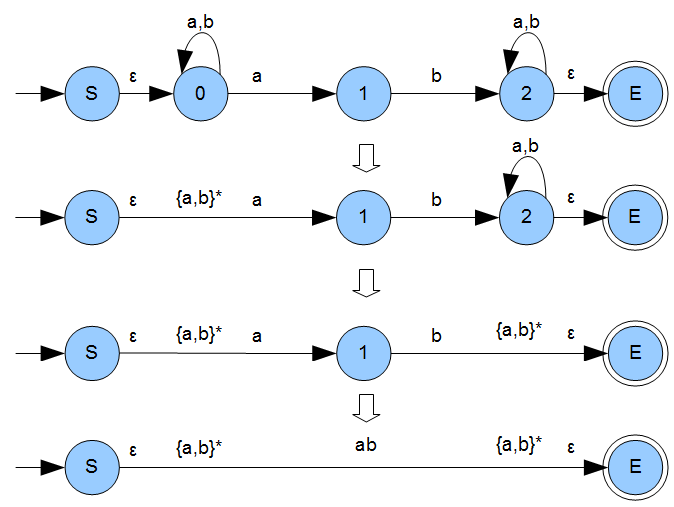
Das alles angewendet auf unseren Graphen führt uns zu folgendem:

Die leeren Worte $\epsilon$ brauchen wir nun nicht mehr und können sie streichen. Korrekt geklammert haben wir den gesuchten, regulären Ausdruck $\alpha=\{a,b\}^{*}\cdot\{ab\}\cdot\{a,b\}^{*}$ und damit gilt: $L(A) = L(\alpha)$. Wir können auch problemlos eine reguläre Grammatik $G$ zum Automaten $A$ angeben um $L(A) = L(\alpha) = L(G)$ zu bekommen. Könnt Ihr mal selbst probieren.

Aufgabe: findet zum Automaten $A$ die Regelmenge der passenden Grammatik

Lösung zeigen

Lernziel 4

Wie zeigt man, dass die regulären Sprache unter den in Satz 8.4.1 genannten Operationen abgeschlossen sind (Beweisidee)?

Was waren nochmal die Operationen in Satz 8.4.1? Ach ja:

Vereinigung, Komplexprodukt, Stern
Durchschnitt, Mengendifferenz, Komplement
Spiegelung

Und was Abgeschlossenheit ist, wisst Ihr doch noch, oder? Die Anwendung der Operationen auf zwei Mengen der selben Klasse führt nicht aus dieser Klasse heraus. Ein einleuchtendes Beispiel sind die ganzen Zahlen $\mathbb{Z}$, die bzgl. Subtraktion, Addition und Multiplikation abgeschlossen sind. Aber nicht bzgl. der Division: $1:3=\frac{1}{3}$ und es gilt $\frac{1}{3}\in\mathbb{Q}$ und $\frac{1}{3}\notin\mathbb{Z}$.

Wie beweisen wir denn nun, dass die regulären Sprachen bzgl. der Operationen abgeschlossen sind? Fangen wir mit dem Komplement an:

Beweisidee zur Abgeschlossenheit bzgl. des Komplements

$B\setminus A=\{x\in B\mid x\notin A\}$, wobei $B\subseteq A$

Was müssen wir zeigen? Es muss gelten $L(A)=L$ und $L(\overline{A})=\Sigma^{*}\setminus L=\overline{L}$. D.h. in $\overline{L}$ liegen alle Worte aus $\Sigma^{*}$, die nicht in $L$ liegen. Das wäre dann unser Komplement.

Es werden zwei vollständige und determinierte Automaten $A$ und $\overline{A}$ konstruiert, die sich nur in ihren Endzuständen unterscheiden. Wir erinnern uns, dass ein Wort $x\in\Sigma^{*}$ nur dann zu einer Sprache $L(A)$ gehört, wenn es ausgehend vom Startzustand den Automaten $A$ in einen Endzustand überführt.

Der Unterschied zwischen den Automaten sind nur ihre Endzustände: für Automat $A$ sind die Endzustände in $F$ und für Automat $\overline{A}$ sind die Endzustände in $Q\setminus F$, d.h. alle Zustände außer den Endzuständen $F$ des Automaten $A$. Die Überführungsfunktionen aus $\delta$ bleiben erhalten. Ein kleines Beispiel um es greifbarer zu machen:

Beispiel: Sei $A$ der Automat von oben mit $A=(\{a,b\},\{0,1,2\},0,2,\delta)$, so wäre $\overline{A}$ der andere Automat mit $\overline{A}=(\{a,b\},\{0,1,2\},0,\{0,1\},\delta)$. Beachtet die Endzustände des Automaten $\overline{A}$.

Ist also ein Wort $x\in\Sigma^{*}$ in der Sprache $L$, so führt es die Maschine $A$ in den Endzustand $2$. Ist es nicht in $L$, so sind wir notgedrungen immer noch in Zustand $0$ oder $1$ unterwegs. Und das sind ja genau die Endzustände unserer Maschine $\overline{A}$, was bedeutet, dass wenn ein Wort nicht in Sprache $L$ ist, so ist es gezwungenermaßen in Sprache $\overline{L}$. Die umgekehrte Richtung gilt ebenfalls, wie man sich leicht vorstellen kann.

Achtung: kontextfreie Grammatiken (Typ-2) sind nicht abgeschlossen bzgl. des Komplement!

Beweisidee zur Abgeschlossenheit bzgl. Vereinigung, Produkt und Stern:

Diese sind bereits nach der Definition der regulären Mengen ebenfalls regulär. Hier müssen wir also nichts mehr tun. Im Skript ist noch eine Beweisidee für die Vereinigung drin, aber vielleicht macht es Sinn diese hier anhand von Beispielen (aus dem Buch von Dirk W. Hoffmann) zu illustrieren.

Beispiel: Nehmen wir zunächst zwei Grammatiken (wir sind wieder bei Grammatiken, nicht mehr bei Automaten) über einem Alphabet $\Sigma$.

$G_1=\{\Pi_1,\Sigma,R_1,S_1\}$ (zur Erinnerung: Nonterminale, Alphabet, Regeln, Start) mit den Regeln

$S_1\rightarrow A_1 B_1$

$A_1\rightarrow ab\mid aA_{1}b$

$B_1\rightarrow c\mid cB_1$

$G_2=\{\Pi_2,\Sigma,R_2,S_2\}$ mit den Regeln

$S_2\rightarrow A_2 B_2$

$A_1\rightarrow a\mid aA_2$

$B_1\rightarrow bc\mid bB_{2}c$

Wichtig: Wie Ihr unschwer erkennen könnt, sind die Grammatiken nur kontextfrei (Typ-2) und nicht regulär. Das ist jedoch für die Beispiele zur Vereinigung, Produkt und Stern nicht schlimm, dafür sind sie abgeschlossen. Sie sind jedoch nicht abgeschlossen für Durchschnitt und Komplement.

Wir gehen davon aus, dass die Nonterminalmengen $\Pi_1$ und $\Pi_2$ keine gemeinsamen Mengen haben.

Vereinigung

Wir müssen also eine Grammatik erzeugen, die uns $L(G_1)\cup L(G_2)$ erzeugt. Dazu werden die Mengen $\Pi_1$ und $\Pi_2$ (Nonterminale), sowie $R_1$ und $R_2$ (Regeln) zu neuen Mengen zusammengefasst. Auch kümmern wir uns um das Startsymbol, welches beide Startsymbole $S_1$ und $S_2$ zusammenfasst. Auch müssen wir eine neue Produktion einführen und wir erhalten:

$G_{1\cup 2}=\{\Pi_1\cup\Pi_2,\Sigma,R_1\cup R_2\cup\{S\rightarrow S_1\mid S_2\},S\}$

Die Regelmenge sieht im Ergebnis wie folgt aus:

$S\rightarrow S_1\mid S_2$

$S_1\rightarrow A_1\mid B_1$

$A_1\rightarrow ab\mid aA_{1}b$

$B_1\rightarrow c\mid cB_1$

$S_2\rightarrow A_{2}B_2$

$A_2\rightarrow a\mid aA_2$

$B_2\rightarrow bc\mid bB_{2}c$

Und diese Grammatik erzeugt uns $L(G_1)\cup L(G_2)$. Sie ist zwar nicht regulär, aber wir können sie durch Einführung von neuen Regeln und Zuständen zu einer regulären Grammatik transformieren.

Die Beweisidee für den Durchschnitt sollten wir aber auch nicht unerwähnt lassen: Ausgehend von zwei Automaten, die unsere Mengen $L$ und $M$ berechnen, werden weitere Automaten für $\overline{L}$ und $\overline{M}$ erzeugt. Zu diesen Mengen werden zwei reguläre Ausdrücke $\alpha$ und $\beta$ konstruiert und diese mittels $\cup$ zu $(\alpha\cup\beta)$ verbunden, was nichts anderes als ${L}\cap{M}$ ist.

Zu diesem Ausdruck wird eine Grammatik $G$ konstruiert, zur Grammatik ein vollständiger Automat $C$, welcher anschließend zu $\overline{C}$ umgeformt wird. Alles zusammengenommen ist dann $L(\overline{C})=\overline{L(C)}=\overline{\overline{L}\cup\overline{M}}=L\cap M$. Ich fand die Darstellung aus dem Buch von Dirk. W. Hoffmann mit dem Beispiel einfacher nachzuvollziehen.

Komplexprodukt

Hier brauchen wir eine Grammatik für $L(G_1)L(G_2)$. Dazu werden wieder die Nonterminale und Regeln zusammengeführt und die Startsymbole durch ein neues ersetzt.

$G_{1\cdot 2}=\{\Pi_1\cup\Pi_2,\Sigma,R_1\cup R_2\cup\{S\rightarrow S_{1}S_2\},S\}$

Und das ist unsere neue Regelmenge:

$S\rightarrow S_{1}S_2$

$S_1\rightarrow A_1B_1$

$A_1\rightarrow ab\mid aA_{1}b$

$B_1\rightarrow c\mid cB_1$

$S_2\rightarrow A_{2}B_2$

$A_2\rightarrow a\mid aA_2$

$B_2\rightarrow bc\mid bB_{2}c$

Auch das sieht gut aus. Nun zum Stern.

Sternoperator: Kleene’sche Hülle

Was brauchen wir? $L(G_1)^{*}$! Wir brauchen hierzu einfach nur neue Ableitungsregeln, die es uns ermöglichen aus dem neuen Startsymbol eine beliebige Anzahl des ursprünglichen Startsymbols zu erzeugen. Die neue Grammatik sieht wie folgt aus:

$G_{1^{*}}=\{\Pi_1,\Sigma,R_1\cup\{S\rightarrow\epsilon\mid SS_1\},S\}$

Und das ist unsere neue Regelmenge:

$S\rightarrow \epsilon\mid SS_{1}$

$S_1\rightarrow A_1B_1$

$A_1\rightarrow ab\mid aA_{1}b$

$B_1\rightarrow c\mid cB_1$

Und fertig!

Weiter geht es mit dem Durchschnitt für reguläre Sprachen.

Beweisidee zur Abgeschlossenheit bzgl. des Durchschnitts:

$B\cap A=\{x\in B\mid x\in A\}$

Mittels der de Morgan’schen Regel gilt: $L\cap M = \overline{\overline{L}\cup\overline{M}}$. Und die Vereinigung haben wir ja bereits in der Definition als regulär drin.

Achtung: kontextfreie Grammatiken (Typ-2) sind nicht abgeschlossen bzgl. des Durchschnitts!

Beweisidee zur Abgeschlossenheit bzgl. der Differenz

$B\setminus A=\{x\in B\mid x\notin A\}$, wobei hier $B$ nicht unbedingt eine Teilmenge von $A$ sein muss.

Es gilt: $L\setminus M=L\cap\overline{M}$

Achtung: kontextfreie Grammatiken (Typ-2) sind nicht abgeschlossen bzgl. des Durchschnitts und somit auch nicht bzgl. der Differenz!

Beweisidee zur Abgeschlossenheit bzgl. der Spiegelung

Es muss also gelten $L$ ist regulär $\Rightarrow L^R = \{a_n,…,a_1\mid a_1,…,a_n\}$ ist regulär.

Ich finde hier den Beweis mittels Automat einfacher. Dazu wird einfach ein neuer Automat, der Umkehrautomat wie folgt gebildet:

$(b,x,a)$ gdw. $(a,x,b)$ (Umkehrung der Zustandsübergänge)
Startzustand $q_0$ wird zum neuen Endzustand
Neuer Startzustand mit $\epsilon$-Übergängen zu allen alten Endzuständen

Damit haben wir unser gespiegeltes Wort. Und da sich ansonsten nichts am Automaten geändert hat, ist die Ergebnismenge weiterhin regulär.

Antwort zum Lernziel: man zeigt die Abgeschlossenheit der regulären Sprachen bzgl. der Operationen, indem man Automaten erstellt, die die Operationen auf den beiden Mengen durchführen. Nach Definition aus dem Beitrag zu KE5 sind die regulären Sprachen, auf denen die Operationen $\cup$, $\cdot$ und $*$ ausgeführt werden ebenfalls regulär. Können wir also die oben genannten Operationen damit „nachbilden“, ist uns der Nachweis gelungen (siehe Beweis zum Durchschnitt).

Lernziel 5

Welche „Probleme“ sind für reguläre Sprachen entscheidbar?

Der Abschnitt ist kurz, aber wichtig! Es gibt bestimmte Probleme auf den regulären Mengen, die entscheidbar sind. Dazu gehören:

$x\in L_1$? (Sprachproblem, gehört das Wort $x$ zur Sprache $L_1$?)

$L_1\subseteq L_2$? (Inkklusionsproblem, ist $L_1$ eine Teilmenge der Sprache $L_2$?)

$L_1=L_2$? (Äquivalenzproblem, ist die Sprache $L_1$ äquivalent zur Sprache $L_2$?)

$L_1=\emptyset$? (Leerheitsproblem, ist die Sprache $L_1$ leer?)

$L_1$ endlich? (Endlichkeitsproblem, ist die Sprache $L_1$ endlich? D.h. $\#L_1\leq\infty$)

Für Typ-2-Sprachen können wir z.B. das Äquivalenzproblem nicht entscheiden.

Antwort zum Lernziel: Das Sprachproblem, das Inklusionsproblem, das Äquivalenzproblem, das Leerheitsproblem und das Endlichkeitsproblem sind für reguläre Sprachen entscheidbar.

Lernziel 6

Wie lautet das Pumping-Lemma für reguläre Sprachen? Wie kann man es verwenden um nachzuweisen, dass eine Sprache nicht regulär ist?

Die Definition im Skript lasse ich mal für zuletzt. Erst einmal: mit dem Pumping Lemma für reguläre Sprachen (für Typ-2-Sprachen gibt es auch eins) haben wir ein Werkzeug an der Hand, mit dem wir nachweisen können, dass eine Sprache nicht regulär ist. Das liegt an der festgelegten Struktur der Produktionen (Regeln) unserer Sprachtypen.

Sieht man sich z.B. die festgelegten Regeln für unsere regulären Sprachen an, so sieht man, dass wir in jedem Schritt ein Terminal und ein Nonterminal erzeugen, wobei das Nonterminal immer an letzter Stelle steht. Abgesehen von der Abschlussregel mit dem leeren Wort $\epsilon$ haben wir hier ein festgelegtes Erzeugungsmuster. Das Nonterminal an letzter Stelle begrenzt die Anzahl der Regeln, die im nächsten Schritt anzuwenden sind und erlaubt uns Rückschlüsse auf die bisher erzeugten Zeichen.

Haben wir bei der Erzeugung eines Wortes mehr Schritte getan, als Nonterminale zur Verfügung stehen, so muss min. ein Nonterminal irgendwo mehrfach aufgetaucht sein. Bildlich gesprochen sind wir also über einen Zyklus im Automaten gestolpert. Denn jeder Automat zu einer regulären Sprache hat auch eine endliche Anzahl an Zuständen.

Beispiel: nehmen wir einfach $G_1$ aus dem vorherigen Beitrag: $G_1=(\Pi,\Sigma,R,S)$ mit $\Pi=\{S,B,C\}$, $\Sigma=\{a,b\}$, Startsymbol $S$ und den Regeln $R$:

$S\rightarrow aB$

$B\rightarrow bC$

$C\rightarrow\epsilon\mid aB$

Damit ist $L(G_1)=\{ab\}*$, also alle Worte über $ab$, d.h. z.B. $ab$, $ababab$ oder $ababababa$. Hier habt Ihr auch euren Zyklus. Wir haben z.B. das Wort $abab$: die Anzahl der Terminale ist größer als die Anzahl der Zustände im Automaten. Damit müssen wir min. einen Zyklus durchlaufen haben.

Jetzt ist der richtige Zeitpunkt für die Definition des Pumping Lemma:

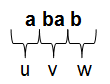
Für jede reguläre Sprache $L$ existiert ein $j\in\mathbb{N}$, so dass sich alle Wörter $\omega\in L$ mit $\mid\omega\mid\geq j$ in der folgenden Form darstellen lassen:

$\omega=uvw$ mit $\mid v\mid\geq 1$ und $\mid uv\mid\leq j$

Dann ist mit $\omega$ auch das Wort $uv^{i}w$ für alle $i\in\mathbb{N}_0$ enthalten.

$j$ wird Pumping-Zahl genannt. Wenden wir die Definition von oben also auf unser Beispiel an, so hat das kleinste Wort mit einem Zyklus die Länge $j=4$ ($abab$). Dann muss das Anfangsstück $u$ mindestens die Länge $1$ aufweisen und in Kombination mit dem Mittelteil maximal $4$ Zeichen lang sein. Wichtig ist, dass $j$ nicht die kleinste Länge haben muss, auf die die Kriterien zutreffen. Es genügt irgendein $j$, das passt und man eine Zerlegung $uvw$ für das Wort zeigen kann.

In unserem Beispiel mit dem Wort $$a ba b$ und $j=4$ haben wir eine:

Es lässt sich der Mittelteil $v$ also beliebig oft wiederholen und das daraus entstandene Wort ist immer noch noch in $L$. Ist das nicht der Fall, so ist die Sprache nicht regulär. Wie man oben am Automaten sehen kann, ist die Kombination $ba$ auch genau unser Zyklus! Wir haben in unserem Wort immer ein $a$ am Anfang und ein $b$ am Ende (unsere $u$ und $w$), während wir den Mittelteil $v$ beliebig oft (oder auch gar nicht) wiederholen können.

Kommen wir nun zu einer kleinen Abweichung von der obigen Grammatik.

Beispiel: $G_2=(\Pi,\Sigma,R,S)$ mit $\Pi=\{S,B,C\}$, $\Sigma=\{a,b\}$, Startsymbol $S$ und den Regeln $R$:

$S\rightarrow aB$

$B\rightarrow bC$

$C\rightarrow\epsilon$

Der einzige Unterschied von $G_1$ zu $G_2$ ist, dass der Zustandsübergang von $C$ keinen Zyklus mehr hat. Der Automat sieht nun wie folgt aus:

Die Sprache $L(G_2)$ besteht also nur aus dem Wort $ab$. Fällt euch was auf? Wir haben keinen Zyklus. Die Sprache ist trotzdem regulär. Was machen wir hier mit unserem Pumping-Lemma? Nichts! Das Pumping-Lemma ist sinnvoll für unendliche Sprachen, endliche Sprachen sind der Definition nach bereits regulär. Das heißt aber nicht, dass das Pumping-Lemma hier nicht auch funktioniert.

Nicht vergessen: wir können mit dem Pumping-Lemma nicht zeigen, dass eine Sprache regulär ist (die Erfüllung des Pumping Lemma ist nicht hinreichend), wir können aber zeigen, dass sie das nicht ist, indem wir uns eine Pumping Lemma Zahl $j$ suchen, für Wörter, die größer sind als $j$ die Zerlegungen durchgehen und sie prüfen. Hat keine unserer unserer Zerlegungen die gewünschte Form, so ist die Sprache nicht regulär (kontextfrei). Warum größer als $j$?

Ganz einfach: für eine reguläre Sprache brauchen wir nur einen endlichen Automaten anzugeben, der für jedes Wort aus der Sprache einen akzeptierenden Zustand hat.

Setzen wir $j$ in unserem Beispiel z.B. auf $\geq 3$, bedeutet es, dass wir für alle anderen Worte $\leq 2$ bereits einen Automaten im Kopf haben, der für alle Wörter keiner als $3$ akzeptierende Zustände hat. Damit ist sind bzgl. der Worte die Sprache bereits als regulär entlarvt. Fehlt uns nur noch der Beweis der Regularität aller anderen Worte der Sprache.

Tja, wie viele Worte haben wir nun mit der Länge $\geq 3$? Keine! Wir haben also nichts mehr zu prüfen, da eine leere Menge ist der Definition nach regulär ist. Also ist die Sprache $L(G_2)$ nicht nur nicht nicht regulär (sorry für das komische Wortkonstrukt), sondern sogar durch die Angabe eines endlichen Automaten regulär. Das ist der Grund für die Regularität von endlichen Sprachen.

Merksatz: Endliche Sprachen sind immer regulär. Wir basteln uns hierzu einfach einen Automaten, der für jedes Wort, dass wir haben (denn die Menge unserer Worte ist endlich) einen akzeptierenden Zustand hat. Auch wenn die Länge der Worte $2^100$ ist, und der Automat Milliarden an akzeptierenden Zuständen hat. Hauptsache sie sind endlich. That’s it.

In der Regel kennen wir das $j$ jedoch nicht, so dass wir nur eine Sprachdefinition, wie z.B. $L=\{(ab)^*\}$ haben und prüfen müssen ob die Sprache regulär ist. Bei Gelegenheit bringe ich hier ein paar explizite Beispiele. Bis dahin begnüge ich mich mit der Antwort zum Lernziel.

Antwort zum Lernziel: Mit dem Pumping Lemma lässt sich nachweisen, dass eine Sprache nicht regulär ist. Der Umkehrschluss gilt nicht, es gibt Sprachen, die nicht regulär sind aber das Pumping Lemma erfüllen. Dazu wird eine Pumping Lemma Zahl $j$ gesucht und für alle Worte, die länger sind als $j$ eine Zerlegung $uvw$ angegeben, so dass man das Midfix $v$ beliebig oft wiederholen kann und sich das Wort immer noch in der Sprache befindet. Tut es das nicht, so ist die Sprache nicht regulär. Wir weisen mit der Angabe von $v$ also quasi einen Zyklus im Automaten nach, mit dem man unendliche Worte durch Wiederholung von $v$ erstellen kann ohne die Sprache zu verlassen. Für endliche Sprachen gilt er Merksatz von oben.

Weiter geht es dann mit den letzten beiden Lernzielen im nächsten Beitrag. Fehler, Ergänzungen, Bermerkungen wie immer bitte ASAP in die Kommentare.

27. Mai 201325. November 2025

TIB: Endliche Automaten und kontextfreie Grammatiken (Lernziele KE6 1/3)

Vorletzte Kurseinheit. Und dazu noch ein eig. sehr schönes Thema. Die letzte KE und diese hier gehören ganz eng zusammen; ich kämpfe noch mit mir nicht einen einzigen Eintrag aus beiden Kurseinheiten zu gießen. Ich empfehle euch beide in einem Tab/Fenster aufzumachen damit Ihr beide Einträge vor der Nase habt und zwischen ihnen blättern könnt wenn in diesem Eintrag auf Sätze aus KE5 Bezug genommen wird.

Leider sind die letzten Kurseinheiten etwas dicker 😉 Kämpfen wir uns also wieder direkt durch die Lernziele.

Lernziel 1

Wie definiert man die von einem endlichen Automaten erkannte Sprache?

In dieser Kurseinheit sind Turingmaschinen mit einem Einweg-Ausgabeband ohne Arbeitsbänder im Fokus. Auch wenn man sie als Turingmaschinen notieren kann, wird eine andere Notation verwendet. Die der endlichen Automaten. Starten wir mit der Definition und einem Beispiel:

Endlicher (nichtdeterministischer) Automat

Quintupel $A=(\Sigma,Q,q_0,F,\delta)$ mit

$\Sigma$ als Eingabealphabet

$Q$ als endliche Menge der Zustände

$q_0\in Q$ als Anfangszustand

$F\subseteq Q$ als Menge der Endzustände

$\delta\subseteq Q\times\Sigma\times Q$ als Überführungsrelation

Dieser Teil der Definition macht euch sicher kaum Probleme, haben wir doch bereits Turingmaschinen in ähnlicher Weise definiert. Die Überführungsrelation führt einfach nur von einem Zustand aus $Q$ zu einem anderen Zustand aus $Q$ bei der Eingabe von einem Element aus dem Eingabealphabet $\Sigma$.

Nun definieren wir noch $\delta$:

$\delta^0=\{(q,\epsilon,q)\mid q\in{Q}\}$ $\delta^{n+1}=\{(p,xa,q)\mid x\in{\Sigma}^{*},a\in{\Sigma},\exists r\in{Q}.(p,x,r)\in\delta^{n}\wedge(r,a,q)\in\delta\}$
$\delta^{*} = \bigcup_{n\geq 0}\delta^n$ ist die transitive Hülle von $\delta$

Oha. Die induktive Definition der Überführungsrelation ist nicht so einfach. Aber warten wir das folgende Beispiel gleich ab, dann wird es klarer. In der transitiven Hülle sind auch indirekte Relationen drin, d.h. erreichen wir z.B. den Zustand $q_2$ bei der Eingabe von $a$ nur über $q_1$ ausgehend vom Startzustand $q_0$, so hätten wir eig. nur die Relationen $(q_0,a,q_1)$ und $(q_1,a,q_2)$. In der transitiven Hülle $\delta^{*}$ haben wir jedoch auch noch das indirekte Tripel $(q_0,a,q_2)$ drin.

Diese Tripel in $\delta^{*}$ können nicht nur einzelne Zeichen aus $\Sigma$ beinhalten, sondern können der Definition nach auch Worte sein. Führt uns z.B. die Eingabe $aaabbb$ zu einem Endzustand, so ist in der transitiven Hülle $\delta^{*}$ auch $(q_0,aaabbb,q)$ drin (wobei $q_0$ ein Anfangs- und $q$ ein Endzustand ist). Wird gleich im folgenden beispiel etwas verständlicher, versprochen.

Kommen wir nun zur akzeptierten Sprache $L(A)$:

$L(A):=\{x\in\Sigma^{*}\mid\exists q\in F.(q_0,x,q)\in\delta^{*}\}$ $L(A):=\{x\in\Sigma^{*}\mid\delta^{*}\cap(\{q_0\}\times\{x\}\times F)\neq\emptyset\}$

Es gilt also $x\in L(A)$ genau dann wenn $x$ den Anfangszustand in einen Endzustand überführt. Damit ist genau das die von dem endlichen Automaten $A$ erkannte Sprache $L(A)$. Nun kümmern wir uns um die Worte determiniert und vollständig.

determiniert, gdw. $\#\{q\in Q\mid(p,a,q)\in\delta\}\leq 1$ für alle $p\in Q,a\in\Sigma$

vollständig, gdw. $\#\{q\in Q\mid(p,a,q)\in\delta\}\geq 1$ für alle $p\in Q,a\in\Sigma$

Gar nicht so schwer: determiniert bedeutet, dass wir ausgehend vom Startzustand $q_0$ das Wort $x$ von links nach rechts ableiten und immer einen Folgezustand haben. Wenn es mal keinen Folgezustand gibt, so ist der Automat nicht vollständig und es gilt $x\notin L(A)$. Gibt es einen Zustand $p_n$ für die Eingabe $x$, wobei $n=lg(x)$ (Länge von $x$), so gilt: $x\in L(A)\Leftrightarrow p_n\in F$. D.h. soviel wie wenn die Länge von $x$ $n$ ist, so muss nach $n$ Schritten der Endzustand $p_n$ erreicht worden sein. Damit ist dann auch $x\in L(A)$. Landet man nach $n$ Berechnungsschritten nicht im Endzustand, so ist $x\notin L(A)$.

Nichtdeterminierte Automaten sind – genauso wie $NTM$ – reine Gedankenmodelle. Hierzu gibt es ein Beispiel im Skript, dass ich auch gerne anführen würde:

Beispiel: $A=(\Sigma,Q,q_0,F,\delta)$ mit

$\Sigma=\{a,b\}$ (Eingabealphabet)

$Q=\{0,1,2\}$ (Zustände)

$q_0=0$ (Startzustand)

$F=\{2\}$ (Endzustand)

$\delta=\{(0,a,0),(0,b,0),(0,a,1),(1,b,2),(2,a,2),(2,b,2)\}$

Wir zeichnen die Zustände als Kreise, weisen Start- und Endzustand entsprechend aus und jeder Übergang von einem Zustand zum anderen wird eine gerichtete und gekennzeichnete Kante zwischen diesen. Gibt es bereits einen Übergang, so müssen wir die Kante mit dem zusätzlichen Zeichen nur noch kennzeichnen.

Dieser ist nicht determiniert. Warum? Weil es für für eine Eingabe und einen Zustand zwei Folgezustände gibt: $(0,a,1)$ und $(0,a,0)$.

Auch ist er nicht vollständig: Warum? Weil wir im Zustand $1$ für die Eingabe $a$ keinen Folgezustand haben.

Wie sieht unsere transitive Hülle $\delta^{*}$ aus? Sie hat z.B. auch noch zusätzlich das indirekten Tripel $(0,b,2)$ drin. Und was ist mit dem $\delta^n$? Dazu kommen wir auch gleich. Ersteinmal stellen wir uns die Frage: Welche Sprache entscheidet der Automat?

Zunächst einmal können wir eine absolut beliebige Kombination aus $a$ und $b$ haben und verweilen im Zustand $0$: ${\{a,b\}}^{*}$. Erst wenn wir zum Zustand $2$ wollen, benötigen wir als Abschluss des ersten Teils der Zeichenkette ein $\{ab\}$. Und dort angekommen sind wir entweder fertig oder können im Zustand $2$ so verweilen, wie wir auch in Zustand $0$ verweilt haben: mit einer beliebigen Kombination aus $1$ und $b$: ${\{a,b\}}^{*}$.

Damit ist die von $A$ erkannte Sprache $L$, d.h. $L(A)={\{a,b\}}^{*}\{ab\}{\{a,b\}}^{*}$

Und nun kümmern wir uns um $\delta^n$ am versprochenen Beispiel (ebenfalls aus dem Skript geklaut).

Beispiel $a^4b^2\in L(A)$?

Wir müssen also schauen ob die Eingabe $x=aaaabb$ uns zu einem Endzustand (ein Zustand aus $F$) bringt oder nicht. In jedem Schritt bringt uns ein Zeichen aus dem Wort zu einem Folgezustand. Und wenn es mal keinen gibt oder wir nach $lg(x)=6$ Schritten noch keinen Endzustand erreicht haben, so ist das Wort nicht Teil unserer Sprache $L(A)$. Versuchen wir es also:

$(0,\epsilon,0)\in\delta^0$

$(0,a,0)\in\delta^1$ da $(0,a,0)\in\delta$

$(0,aa,0)\in\delta^2$ da $(0,a,0)\in\delta$

$(0,aaaa,0)\in\delta^3$ da $(0,a,0)\in\delta$

$(0,aaaaa,1)\in\delta^4$ da $(0,a,1)\in\delta$

$(0,aaaab,2)\in\delta^5$ da $(1,b,2)\in\delta$

$(0,aaaabb,2)\in\delta^6$ da $(2,b,2)\in\delta$

Wir sehen also, dass wir Ausgehend vom Startzustand $0$ zum Zustand $2$ gelangen, welcher ein Endzustand ist. Es liegt daher $(0,aaaabb,2)\in\delta^{*}$, woraus folgt, dass $a^4b^2\in L(A)$! Um zu zeigen, dass ein Wort zur Sprache gehört, müssen wir also einfach nur eine Zustandsfolge angeben, die die zu prüfende Eingabe in den Endzustand überführt. Braucht Ihr noch ein Beispiel um zu zeigen, dass eine Zeichenfolge nicht in $L(A)$ ist? Gerne.

Beispiel: $a^4\in L(A)$?

Spielen wir den Graphen mit der Eingabe $aaaa$ durch, so sehen wir, dass wir nie in im Endzustand $2$ landen. Wir bleiben immer nur in $0$ oder $1$. Damit ist $a^4\notin L(A)$? Probiert die nächsten beiden mal selbst.

Übung: $a^2 b^2\in L(A)$ $(aabb)$?

Lösung zeigen

Übung: $(ba)^3\in L(A)$ $(bababa)$?

Lösung zeigen

Übung: $(ba)\in L(A)$ $(ba)$?

Lösung zeigen

Antwort zum Lernziel: Damit ist die von einem endlichen Automaten $A$ erkannte Sprache $L$ die Menge der Worte über dem Alphabet $\Sigma$, die ausgehend von einem Startzustand $q_0$ den Automaten in einen Endzustand $q$ überführt und dabei nicht mehr Berechnungsschritte braucht als die Eingabe lang ist.

Lernziel 2

Wie kann man zu einem nichtdeterminierten endlichen Automaten einen determinierten konstruieren, der dieselbe Sprache erkennt?

Im Beitrag zu KE5 haben wir es bereits angedeutet: die Regeln aus den Grammatiken sind nichts weiter als Überführungsrelationen in Maschinen von einem Zustand zum anderen. Aus diesem Grund können wir rechtslineare Normalformgrammatiken in Automaten überführen. Dazu brauchen wir folgendes:

Transformation $T$ mit $T((\Pi,\Sigma,R,S)):=(\Sigma,\Pi,S,F,\delta)$ mit

$F=\{A\in\Pi\mid (A\rightarrow\epsilon)\in R\}$ und
$\delta=\{(A,a,B)\in\Pi\times\Sigma\times\Pi\mid (A\rightarrow aB)\in R\}$

Wir transformieren damit eine rechtslineare Normalformgrammatik in einen Automaten, so dass $L(G)=L(T(G))$ gilt. Die Definition von $F$ (unseren Endzuständen im Automaten) besagt lediglich, dass in die Menge der Endzustände unseres Automaten das Nonterminal reingehört. was auch als Regel für ein Nonterminal in den Regeln der Grammatik vorhanden ist und auf $\epsilon$ zeigt.

Mit $\delta$ ist es ähnlich. In die Überführungsrelationen gehören alle Regeln rein, die auf ein Terminal (unsere Eingabe im Automaten) und ein Nonterminal (unser Zustand im Automaten) zeigen. Das ist dann unser Zustandsübergang. Am besten ein Beispiel, oder? Nehmen wir dazu doch einfach die Grammatik, die wir im vorherigen Beitrag verwendet haben.

Beispiel: $G_1=(\Pi,\Sigma,R,S)$ mit $\Pi=\{S,B,C\}$, $\Sigma=\{a,b\}$, Startsymbol $S$ und den Regeln $R$:

$S\rightarrow aB$

$B\rightarrow bC$

$C\rightarrow\epsilon\mid aB$

Wir müssen also aus der rechtslinearen Normalformgrammatik $G_1$ einen endlichen Automaten basteln. Weder am Alphabet $\Sigma$, noch an den Zuständen (Nonterminalen) $\Pi$ oder am Startzustand $S$ haben wir was zu kamellen. Wir brauchen die Menge der Endzustände $F$ und unsere Überführungsrelationen $\delta$.

Fangen wir mit dem Endzustand $F$ an. Schaut noch einmal die Definition von $F$ oben an. Wir suchen also in den Regeln $R$ unserer Grammatik $G_1$ nach der Regel von der Form $(A\rightarrow\epsilon)$. Die einzige Regel, die so aussieht ist die Regel für $C\rightarrow\epsilon\mid aB$. Damit haben wir den Endzustand der Grammatik $C$ nun in unserer Automaten-Menge $F$. Hätten wir mehr Regeln, die auf ein $\epsilon$ zeigen, so hätten wir auch mehr Endzustände.

Jetzt die Überführungsrelationen $\delta$: wir transformieren alle Regeln der Grammatik mit der Form $(A\rightarrow aB)$ in die Überführungsrelation für dem Automaten mit der Form $(A,a,B)$:

$S\rightarrow aB\Rightarrow(S,a,B)$

$B\rightarrow bC\Rightarrow(B,b,C)$

$C\rightarrow aB\Rightarrow(C,a,B)$

That’s it. Wie sieht der Automat nun aus? So:

Fertig! Wir sehen auch hier, dass er nicht vollständig ist: es fehlt im Zustand $S$ der Folgezustand für die Eingabe eines $b$. Aber er ist determiniert, da wir nicht mehrere Folgezustände für eine Eingabe haben.

Nachdem das nun geklärt ist, kümmern wir uns um die Überführung von nichtdeterminierten Automaten in determinierte. Der Vorteil von letzteren liegt darin, dass diese sich mittels Boole’schen Schaltwerken realisieren lassen. Wäre doch schön wenn wir dazu die nichtdeterminierten Automaten in determinierte überführen könnten…

Beispiel: der Automat aus dem ersten Beispiel mit $A=(\Sigma,Q,q_0,F,\delta)$ mit

$\Sigma=\{a,b\}$ (Eingabealphabet)

$Q=\{0,1,2\}$ (Zustände)

$q_0=0$ (Startzustand)

$F=\{2\}$ (Endzustand)

$\delta=\{(0,a,0),(0,b,0),(0,a,1),(1,b,2),(2,a,2),(2,b,2)\}$

und dem zugehörogen Graphen

Die Menge der neuen Zustände ist maximal $2^Q = 2^3 = 8$. Wobei wir nicht alle benötigen werden. Dazu stellen wir eine Tabelle auf, die uns am Ende zeigt welche Übergänge und welche Zustände wir haben. Wir fangen einfach mal an, die Inhalte der Spalten erschließen sich dann direkt:

V	W		W\V
P	a	b
{0}	{0,1}	{0}	{0,1}

In der ersten Zeile, in Spalte $P$ steht der Startzustand. In Spalte $a$ und $b$ stehen die jeweils erreichbaren Zustände bei der jeweiligen Eingabe, ausgehend vom Zustand in Spalte $P$. D.h. ausgehend von Startzustand $0$ erreichen wir bei der Eingabe von $a$ Folgezustand $0$ und $1$ und bei der Eingabe von $b$ nur Zustand $0$. In der Spalte $W\setminus{V}$ befindet sich die Elemente der Menge $W=\{\{0,1\},\{0\}\}$ ohne die Elemente der Menge $V=\{\{0\}\}$, also nur $W\setminus{V}=\{\{0,1\}\}$. Damit haben wir die erste Zeile aufgebaut.

Für die Spalte $P$ in der zweite Zeile nehmen wir ein Element aus der Menge $W\setminus{V}=\{\{0,1\}\}$. Viel Auswahl haben wir hier nicht (hätten wir eine, so wäre die Auswahl willkürlich, sie würde nur die Reihenfolge der Zeilen beeinflussen). Nun werden wieder die erreichbaren Folgezustände, ausgehend von Startzustand $0$ und $1$ bei der Eingabe von $a$ und $b$ in den folgenden Spalten notiert und in der letzten Spalte wieder $W\setminus{V}$ eingetragen. Das machen wir solange, bis die Menge $W\setminus{V}$ leer ($W\setminus{V}=\emptyset$) ist. Am Ende haben wir die folgende Tabelle:

V	W		W\V
P	a	b
{0}	{0,1}	{0}	{0,1}
{0,1}	{0,1}	{0,2}	{0,2}
{0,2}	{0,1,2}	{0,2}	{0,1,2}
{0,1,2}	{0,1,2}	{0,2}

Aus dieser können wir nun alle notwendigen Zustände (Spalte $P$) und die Folgezustände (Spalten $a$ und $b$) ableiten. Alle Zustände aus Spalte $P$, die die Zahl eines Endzustandes ($2$) des ursprünglichen Automaten beinhalten, werden ebenfalls zu Endzuständen. Am Ende kommt daher folgender Graph raus:

Wenn wir die Wertetabelle dazu aufstellen sehen wir auch, dass wir einen Zustand wegkürzen können (wie in Computersysteme 1 und 2).

Zustand	Folgezustand bei Eingabe von „a“	Folgezustand bei Eingabe von „b“
0	01	0
01	01	02
02	012	02
012	012	02

Zustand $02$ und $012$ sind äquivalent und damit kürzbar (wenn man zur $b$-Kante von $02$ noch $a$ hinzufügt).

Antwort zum Lernziel: zu einem nichtdeterminierten Automaten kann man einen determinierten Automaten konstruieren, der dieselbe Sprache erkennt, indem man eine neue Zustandsmenge definiert, die maximal aus der Potenzmenge $2^Q$ der ursprünglichen Zustände $Q$ führt. Die Menge der benötigten Zustände ergibt sich aus allen erreichbaren Zuständen.

Diese neuen Automaten werden Potenzautomaten genannt. Damit lässt sich festhalten, dass man zu jedem endlichen, nicht-deterministischen Automaten einen deterministischen Automaten angeben kann, der die selbe Sprache erkennt.

Da die Namen der neuen Zustände aus den Namen der Ursprungszustände bestehen, können die gerichteten Kanten auch zu den neuen Zuständen problemlos gezogen und so die Zustandsübergänge im neuen Graphen modelliert werden. Durch die Benennung lassen sich auch die Endzustände im neuen, deterministischen Graphen identifizieren: jeder neue Zustand, der in seinem neuen Namen den Namen eines ursprünglichen Endzustands beinhaltet, wird ebenfalls ein Endzustand.

Das war der erste Teil von KE6. Wer Fehler findet: ab in die Kommentare.