TIB: Grammatiken und reguläre Sprachen (Lernziele KE5, Update 6)

Update 2: Markus hat eine Ungenauigkeit im Lernziel 8 gefunden. Ist korrigiert, Danke.

Update: Beispiel für die regulären Ausdrücke, sowie Gleichungen für die Funktion $L$ aus Lernziel 5 hinzugefügt. Ebenfalls Antworten zu allen Lernzielen verfasst.

Noch drei Kurseinheiten, dann ist TIB auch schon vorbei. In dieser Kurseinheit geht es um Grammatiken. Häufig wird in der Literatur zunächst die Grammatik eingeführt und anschließend die Komplexität, aber das soll uns hier nicht weiter stören. Also wieder entlang der Lernziele.

Lernziel 1

Was ist eine Grammatik $G$, wie definiert man die Sprache $L(G)$?

Eine Grammatik ist ein Modell zur Definition konkreter Sprachen. Die erste Definition im Skript ist die der formalen Sprache (letzter Punkt ist der aus dem Skript, alle anderen sind geklaut aus dem Buch von Dirk. W. Hoffmann).

Automat: Maschine zum Erkennen von Sprachen.

Alphabet $\Sigma$, endliche Menge von Symbolen.

Jedes Element $a$ ist ein Zeichen des Alphabets.

Jedes Element $\omega$ ist ein Wort über $\Sigma$.

Jede Teilmenge $L\subseteq\Sigma^{*}$ ist eine formale Sprache über $\Sigma$.

$\Sigma^{*}$ nennt man auch Kleen'sche Hülle. Dort sind alle endlichen Symbolsequenzen drin, die wir mit den Symbolen aus $\Sigma$ basteln können. Auch ist dort das leere Wort $\epsilon$ enthalten (im $\Sigma^{+}$ jedoch nicht). Sagen wir z.B., dass $L$ über dem Alphabet $\Sigma=\{0,1,2,...,9\}$ die Menge der Ziffernfolgen ist, die einer Primzahl entsprechen, so wäre z.B. $2,3,5,7,...\in L$, während $1,4,6,8,...\notin L$ ist.

Uns geht es aber nicht um die Bedeutung der Worte, sondern um die syntaktischen Anteile.

Überabzählbarkeit

Ein wichtiger Aspekt ist, dass die Menge der formalen Sprachen über $\Sigma$ (also $L_{\Sigma}$) überabzählbar unendlich ist. Für eine Abzählbarkeit brauchen wir eine Bijektion zwischen den natürlichen Zahlen $\mathbb{N}$ und der abzuzählenden Menge. Da jedoch die menge aller Sprachen über einem Alphabet $L_{\Sigma}$ gleich der Mächtigkeit aller Teilmengen von $\Sigma^{*}$ ist, gilt $L_{\Sigma}=P(\Sigma^{*})$. Das $P$ steht für Potenzmenge. Und da Potenzmengen einer beliebigen Menge eine größere Mächtigkeit haben, als die menge selbst ist $L_{\Sigma}$ überabzählbar. Das Beweisverfahren vom zweiten Cantor'schen Diagonalargument findet hier Anwendung.

Kommen wir aber nun zu dem Kerl, der das ganze verbrochen hat: Noam Chomsky. Von ihm stammen auch ein paar spannende Bücher. Der Kerl lebt, wie Stephen A. Cook aus dem vorherigen Beitrag zu KE4, auch noch und lehr am MIT. Mit etwas Kleingeld für die Studiengebühren oder genügend Gehirnschmalz für das Doc-Program des MIT kommt Ihr also noch in den Genuss seiner Lehren.

Der Typ hat also ein einfaches, formales Modell einer Grammatik eingeführt, mit dem man Grundstrukturen einer Sprache beschreiben kann. Im Skript ist die Grammatik als Virertupel definiert, wie in den meisten anderen Büchern auch. Hier lässt es sich also sehr gut auch mit Zusatzliteratur arbeiten. Allgemein halte ich Teil B der theoretischen Informatik für "gelungener". Ob das nun daran liegt, dass es wirklich besser ist oder ich mich mittlerweile von TIA habe abstumpfen lassen, möchte ich an dieser Stelle nicht weiter analysieren.

Definieren wir also die Grammatik als Vierertupel $G=(\Pi,\Sigma,R,S)$:

$\Pi$ Nichtterminalalphabet, endliche Variablenmenge (Platzhalter, auch Nonterminalsymbole genannt. Lassen sich ersetzen)

$\Sigma$ Terminalalphabet, $\Pi\cap\Sigma=\emptyset$ (nicht weiter ersetzbare Sprachberstandteile, auch Terminale genannt).

$R$ Regelmenge/Produktion mit $R\subseteq((\Sigma\cup\Pi)^{*}\setminus{\Sigma^*})\times(\Sigma\cup\Pi)^{*}$ (nicht erschrecken, Erklärung kommt gleich)

$S\in\Pi$ Startsymbol (damit beginnt immer die Ableitung)

Das ist auch gleichzeitig die Definition der Typ-0-Grammatik. Wahrscheinlich hängt Ihr gerade an der Definition der Regelmenge, oder? Wir definieren hier eine Ableitungsrelation. Es gilt zudem $x\Rightarrow^{*}y$ gdw. das Wort $y$ aus dem Wort $x$ in endlich vielen Schritten anhand der Regeln aus $R$ abgeleitet werden kann.

Beispiel: $G=(\Pi,\Sigma,R,S)$ mit $\Pi=\{S,L,R\}$, $\Sigma=\{\#,a\}$ und Regeln $R$ (KE5, S. 9)

$S\rightarrow\#aL\#$

$aL\rightarrow La$

$\#L\rightarrow\#R$

$Ra\rightarrow aaR$

$R\#\rightarrow L\#$

$R\#\rightarrow\#$

Aus diesen Regeln können wir nun Zeichenfolgen ableiten, die zur Sprache $L$ mit der Grammatik $G$ gehören, d.h. Fragen beantworten, wie z.B. $\#aa\#\in L(G)$? Wir müssen nur aus $\#aL\#$ nach endlich vielen Schritten $\#aa\#$ anhand dieser Regeln erzeugen können. Ist das der Fall, so haben wir $\#aa\#\in L(G)$ bewiesen (und ja, es ist tatsächlich $\#aa\#\in L(G)$, probiert es mal selbst).

Übung: $\#aa\#\in L(G)$?

Lösung zeigen

Eine weitere, spannende Definition ist, dass die

von Typ-0-Grammatiken erzeugten Sprachen genau die rekursiv aufzählbaren (semi-entscheidbaren) Wortmengen sind.

Beweisidee: Hierzu wird für eine Bandmaschine eine Grammatik konstruiert, wobei die Regeln der Grammatik die Einzelschrittrelationen der Maschine sind. Die Sprache ist dann genau die Menge der von der Maschine erzeugten Worte. In umgekehrter Richtung wird eine $NTM$ erstellt, die vom Startsymbol ausgeht die Regeln als Einzelschrittrelationen anwendet und anhält wenn das Eingabewort abgeleitet wurde. Nehmen wir also an, dass unsere Maschine aus der Eingabe $aa$ in einem Schritt eine Ausgabe $aaaa$ erzeugt. Das entspräche dann eine Regel in unserer Grammatik: $aa\rightarrow{aaaa}$.

Achtung: Die Menge der rekursiv aufzählbaren (semi-entscheidbaren) Sprachen ist gegenüber

• Kleene'scher Hüllenbildung,
• Konkatenation,
• Schnitt und
• Vereinigung

abgeschlossen, nicht jedoch gegenüber dem Komplement (geklaut aus der Wikipedia). Da das aber nicht so deutlich im Skript raus kam, wollte ich das hier etwas hervorheben.

Antwort zum Lernziel: eine Grammatik $G$ ist ein Modell zur Definition konkreter Sprachen. Sie ist ein 4-Tupel mit Terminalen, Nonterminalen, dem Alphabet und dem, was eine Grammatik erst ausmacht: den Regeln. Mittels diesen Regeln, auch Produktionen genannt, wird eine Sprache $L(G)$ erzeugt, d.h. eine Sprache $L$ über der Grammatik $G$.

Lernziel 2 (Update)

Welche Sprachklasse wird durch Grammatiken definiert?

Hier schwimme ich gerade etwas, da ich nichts mit der Frage anzufangen weiß. Grammatiken definieren unterschiedliche Sprachklassen. Je nach gewählter Grammatik werden unterschiedliche Sprachklassen (entscheidbare oder semi-entscheidbare Sprachen) definiert. Wer die Frage anders interpretiert und eine andere Antwort hat, bitte in die Kommentare damit.

Wieder mal ein großer Dank an Barbara, mit der die Antwort zum Lernziel erarbeitet wurde.

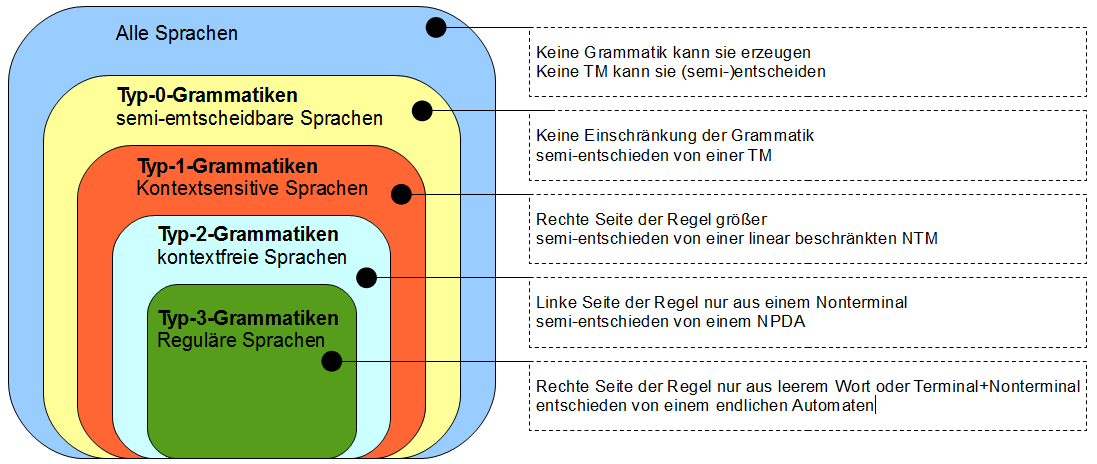
Zunächst einmal noch zur Erinnerung: Die Sprachklassen sind unsere Sprachen, die durch Typ-X-Grammatiken definiert werden. Wir fangen ab Typ-0 an zu zählen, hierzu gehört jede Grammatik, d.h. die absolute Ober-Sprachklasse, die durch Grammatiken definiert wird ist die Typ-0-Sprachklasse. Erst durch Einschränkung unserer Grammatiken zu Typ-1-, -2-, und -3-Grammatiken werden weitere Sprachklassen, eben die Typ-1-, -2-, und -3-Sprachen, definiert, die aber alle eine echte Teilmenge der Typ-0-Sprachklasse sind (diese Inklusionsberziehung ist wichtig, daher merken!).

Nicht falsch verstehen: es gibt auch Sprachen, die nicht von Grammatiken erzeugt werden können (Überabzählbarkeit der Potenzmenge, aber dazu kommen wir später noch). Die Typ-0-Sprachen sind eine echte Teilmenge dieser. In den folgenden Beiträgen wird die Beziehung zwischen den einzelnen Sprachklassen noch deutlicher hervorgehoben, also noch etwas Geduld 😉

Durch was ist die Oberklasse Typ-0, die von Grammatiken erzeugt werden kann, also definiert? Durch eine Turingmaschine, die hält wenn es ein Wort der Typ-0-Sprachklasse akzeptiert und nicht hält (oder sich in einem anderen Zustand befindet) wenn das Wort nicht aus der Typ-0-Sprachklasse ist. Das ist genau die Definition von semi entscheidbaren/rekursiv aufzählbaren Wortmengen: die Typ-0-Sprachen sind genau die von Turingmaschinen akzeptierten Sprachen.

Beweisidee

$TM\rightarrow Grammatik$

Das ist die eine Richtung. Zu einer Turingmaschine $M$ wird eine Grammatik $G$ erzeugt, deren Regeln im wesentlichen die Einzelschrittrelationen sind. Die von der Grammatik $G$ erzeugte Sprache $L(G)$ ist dann genau die Menge der Worte, die $M$ erzeugt.

Vorgehensweise: die Grammatik simuliert mit ihren Ableitungsregeln die Einzelschrittrelationen (Konfigurationsübergänge) der TM. Dabei werden alle möglichen Eingabewörter, Anfangskonfigurationen und die Konfigurationsübergänge als Regeln konstruiert (Nonterminal als Zustand und Folgezustand, Terminal als Eingabezeichen). Dabei wird die Akzeptanz eines Wortes durch das Löschen von Nonterminalen ($C\rightarrow\epsilon$) simuliert und der Ableitungsvorgang so gestoppt.

Damit erzeugt die Grammatik $G$ genau die Worte, die von der TM $M$ akzeptiert werden.

$Grammatik\rightarrow TM$

Für die umgekehrte Richtung wird eine NTM $T$ zu einer Typ-0-Grammatik $G$ erzeugt, welche vom Startsymbol der Grammatik ausgehend die Regeln der Grammatik anwendet und anhält wenn das Wort abgeleitet wurde. Anschließend wir die NTM durch eine TM simuliert.

Vorgehensweise: Die TM simuliert die Ableitungsregeln. Dabei werden ableitbare Worte von der TM schrittweise auf das Hilfsband (man könnte auch ohne Hilfsband arbeiten) geschrieben und mit der Eingabe verglichen. Die Maschine akzeptiert das Wort, bzw. terminiert im Endzustand genau dann wenn $\omega\in L(G)$.

Damit akzeptiert die TM genau die Worte, die von der Grammatik erzeugt werden.

Beispiel: kontextsensitive Grammatik $G_0=(\Pi,\Sigma,R,S)$ mit $\Pi=\{S,B,C\}$, $\Sigma=\{a,b\}$ und Regeln $R$

$S\rightarrow aSBC\mid aBC$

$aB\rightarrow ab$

$bB\rightarrow bb$

$bC\rightarrow bc$

$cC\rightarrow cc$

$CB\rightarrow BC$

Diese Grammatik $G_0$ erzeugt die fiese, kontextsensitive Typ-0-Sprache $L_0=\{a^n b^n c^n\mid n\in\mathbb{N}\}\Rightarrow(abc,aabbcc,...)$. Nun müssen wir zu der Grammatik eine Turingmaschine angeben, die  ein Wort aus dieser Sprache durch erreichen des Endzustands akzeptiert und ansonsten in einem anderen Zustand hält oder nicht terminiert.

Exkurs:

Es stellt sich die Frage, warum müssen wir eine Turingmaschine angeben? Warum geht nichts anderes? Leider haben wir noch nicht die einzelnen Sprachklassen charakterisiert, evtl. wäre es dann bereits jetzt klar. Die Turingmaschine ist das mächtigste Werkzeug das wir haben, sie ist genauso mächtig wie Registermaschinen. Nur, dass Registermaschinen auf Zahlen operieren und Turingmaschinen auf Worten.

Und selbst mit den Turingmaschinen können wir nicht alle Sprachen angeben, denn die Anzahl der Turingmaschinen ist, wie wir wissen, abzählbar unendlich (zweites Diagonalrgument von Cantor). Die Menge aller Sprachen über $\Sigma^{*}$ ist es jedoch nicht (Potenzmenge, siehe oben). Damit können wir, wie erwähnt, nicht alle Sprachen mit Turingmaschinen akzeptieren. Wenn wir die Turingmaschine einschränken, können wir eine immer kleinere Menge innerhalb dieser Obersprachklasse (Typ-0) abdecken, bis wir irgendwann bei den regulären Sprachen (Typ-3) angelangt sind, die von einem endlichen Automaten akzeptiert wird, was im Prinzip nichts weiter ist, als eine maximal eingeschränkte TM.

Aber weiter im Text: Was wir nun tun müssen, ist es die Ableitungssequenz umzukehren. Denn unsere TM nimmt ein Wort entgegen anstatt es zu produzieren. Dazu muss es das Wort in das Startsymbol zurückführen. Wenn es der TM gelungen ist, gilt das Wort als akzeptiert. Können mehrere Regeln angewandt werden, so müssen wir unsere TM als NTM konstruieren.

Wir haben uns zwar darauf beschränkt Einband-TM zu betrachten, aber für die Grammatik $G_0$ war ich etwas faul und habe auf ein Arbeitsband zurückgegriffen. Mit etwas mehr Zuständen schaffen wir das ganze Spiel auch auf einer Einband-TM. In der folgenden Grafik wird die TM aufgezeigt, die unsere Sprache akzeptiert (ich habe mein neues Spielzeug benutzt, kann ich nur empfehlen). Das JFLOP-File könnt Ihr hier downloaden.

Erklärung der Grafik: $a;a,R\mid B;A.R$ bedeutet z.B. Lese auf dem Eingabeband ein $a$ und gehe auf diesem nach rechts. Lese gleichzeitig auf dem Hilfsband ein $B$ (Blank), schreibe ein $A$ und gehe auf dem Hilfsband nach rechts.

Funktionsweise: wir laufen das Wort ab und schreiben so viele $A's$ auf das Hilfsband, wie wir $a's$ auf dem Eingabeband haben. Anschließend gehen wir die $b's$ durch und ersetzen die gleiche Anzahl an $A's$ auf dem Hilfsband, wie $b's$ auf dem Eingabeband vorhanden sind durch $C's$. Nun werden die $c's$ auf dem Eingabeband eingelesen und die gleiche Anzahl der $C's$ auf dem Hilfsband gelöscht.

Jetzt wandern wir auf beiden Bändern so weit zurück, wie unser Eingabewort lang ist. Finden wir dann nur noch Blanks auf dem Hilfsband und sind wir am Anfang unseres Eingabewortes angelangt, wird das Wort akzeptiert.

Ladet euch die Datei für das JFLOP herunter und probiert es selbst aus (Links zu JFLOP und der Datei oberhalb der Grafik).

Antwort zum Lernziel: die Typ-0-Grammatiken definieren die Typ-0-Sprachklasse. Diese Sprachen sind genau die von Turingmaschinen akzeptierten/semi entscheidbaren/rekursiv aufzählbaren Wortmengen.

Sie bilden die Oberklasse aller Sprachen, jedoch kann es auch Sprachen geben, die nicht von Grammatiken erzeugt werden können. Dies wird mit dem gleichen Verfahren bewiesen, wie es auch im zweiten Diagonalargument von Cantor angewandt wurde: es gibt einfach mehr Sprachen (Produktmenge über $\Sigma$), als es Turingmaschinen geben kann (Stichwort: Überabzählbarkeit).

Lernziel 3

Was sind Typ-1-, Typ-2-, Typ-3-Grammatiken?

Neben den Typ-0-Grammatiken gibt es auch noch weitere. Das ist dann die Chomsky-Hierarchie. Der werte Herr - Sprachwissenschaftler - hat 1957 ein Regelwerk erstellt um die Grammatiken in vier Klassen einzuteilen. Diese sind wie folgt:

• Typ-0-Grammatiken: Phrasenstrukturgrammatiken
  Die haben wir eben kennengelernt. Jede Grammatik ist auch immer eine Typ-0-Grammatik. Es gibt keine weiteren Einschränkungen als die erste Definition zum Vierertupel $G=(\Pi,\Sigma,R,S)$ in diesem Beitrag.
  Automat: Zu jeder Typ-0-Sprache existiert eine TM, die diese Sprache akzeptiert (eine TM ist unser stärkstes Berechnungsinstrument). Da wir eine NTM durch eine TM simulieren können (die TM simuliert einfach alle Berechnungspfade der NTM, können wir hier uns auf eine TM beschränken).

 

• Typ-1-Grammatiken: Kontextsensitive Grammatiken (kontextsensitive Sprache)
  Für die Produktionsbeziehungen $l\rightarrow r$ gilt die Beziehung $\mid r\mid\geq\mid l\mid$. D.h. die Anwendung der Produktion führt nie zu einer Verkürzung der Zeichenkette. Ganz einfach, oder?
  Beispiel: $aA\rightarrow aBb$
  Automat: Zu jeder Typ-1-Sprache existiert eine linearbeschränkte TM, die diese Sprache akzeptiert. Die lineare Beschränkung ist der Tatsache geschuldet, dass wir die Grammatik eingeschränkt haben. Die rechte Seite der Produktion wird nie kleiner. Weil wir in der TM die Berechnung umkehren (wir leiten in der Maschine ein gegebenes ein Wort zu seinem Ursprung, statt wie in der Grammatik den Ursprung zum Wort), können wir nie mehr Zeichen auf dem Band bekommen als die Eingabe initial lang war.

 

• Typ-2-Grammatiken: Kontextfreie Grammatiken (kontextfreie Sprache)
  Die linke Seite der Produktionsregeln besteht immer nur aus einer einzigen Variable, es gilt also: $l\rightarrow r\Rightarrow l\in\Pi$. Auch nicht viel schwerer als Typ-1.
  Beispiel: $A\rightarrow aBb$.
  Automat: Zu jeder Typ-2-Sprache existiert ein nichtdeterministischer Kellerautomat, der diese akzeptiert. Der Kellerautomat ist weniger mächtig als die TM (zumindest mit nur einem Speicher), wir können uns also auf ein weniger mächtiges Konstrukt stützen. Warum? Weil das wieder der noch mehr eingeschränkten Grammatik geschuldet ist. Aber normale Automaten reichen nicht aus, da hier beliebig viele Nonterminale auftreten können. Wir brauchen also noch einen Speicher. Da wir uns auf Linksableitungen beschränken (das am links stehende Nonterminal wird ersetzt) können und somit immer nur auf das erste Zeichen im Kellerspeicher zugreifen, können wir diese Linksableitungen einer kontextfreien Grammatik mit unserem Kellerautomaten (NTM mit einem Einweig-Eigabeband und einem Kellerspeicher) simulieren.

 

• Typ-3-Grammatiken: Reguläre Grammatiken (rechtslineare Sprache)
  Sie sind zunächst kontextfrei und die rechte Seite der Produktion besteht entweder aus einem leeren Wort $\epsilon$ oder einem Terminalsymbol, dem ein Nichtterminalsymbol folgt. Formal: $l\rightarrow r$ mit $l\in\Pi$ und $r\in\{\epsilon\}\cup\Sigma\cdot\Pi$ (Danke Gerald, vorher stand da $r\in\{\epsilon\}\cup\Sigma\cup\Pi$, blödes CopyPaste). Das war jetzt etwas schwieriger. Wenn man die Definition langsam liest, erschließt sich einem der Satz etwas besser.
  Beispiel: $A\rightarrow aB$
  Automat: Zu jeder Typ-3-Sprache existiert ein endlicher Automat, der diese akzeptiert. Noch eine weitere Einschränkung. Hier brauchen wir nicht einmal einen Speicher, sondern kommen mit Zuständen aus.

 

Nochmal zur Erinnerung: ein Terminalsymbol ist ein Symbol, dass nicht weiter ersetzt werden kann. Ein Nichtterminalsymbol jedoch ist ein Platzhalter, den man durchaus ersetzen kann.

Zwischen den Sprachen gilt die folgende echte Inklusionsbeziehung: $L(Typ-0)\supset L(Typ-1)\supset L(Typ-2)\supset L(Typ-3)$. Grafisch dargestellt sieht der ganze Spaß so aus:

Im Skript wird ebenfalls eine Verbindung zwischen den Komplexitätsklassen und den Sprachen in der Chomsky-Hierarchie konstruiert, so dass folgende Aussagen äquivalent sind:

$L$ ist eine Typ-1-Sprache (kontextsensitiv).

$L\in NBAND(n)$

Das liegt an folgenden Dingen: keine Regel kann das Wort verkürzen, außer $S\rightarrow\epsilon$. Damit haben wir $lg(x)\leq lg(y)$ (wir leiten von $x$ auf $y$ ab) wenn wir nicht auf ein leeres Wort ableiten. Haben wir zudem z.B. eine Eingabe $x$ von der wir prüfen wollen ob sie zu der Sprache $L(G)$ gehört oder nicht, leiten wir ausgehend vom Startsymbol ab. Da die Länge des abgeleiteten Wortes aufgrund der Einschränkung für Typ-1-Sprachen sich nie verkürzen kann, können wir die Berechnung verwerfen wenn wir ein Wort ableiten, dass länger als unsere Eingabe ist.

Noch eine Kleinigkeit: wegen dem Satz von Savitch ist auch jede kontextsensitive Sprache in Exponentialzeit und $BAND(n^2)$ entscheidbar.

Antwort zum Lernziel: die Grammatiken werden, ausgehend von Typ-0, immer restriktiveren Einschränkungen für die Produktionsregeln unterworfen. Dadurch wird es möglich die Obermenge der Typ-0-Sprachen (semi-Entscheidbarkeit) immer weiter einzuschränken, bis man letztlich zu den Typ-3-Sprachen (reguläre Sprachen, vollständig entscheidbar durch einen endlichen Automaten) kommt. Es ergibt sich so eine echte Inklusionsbeziehung zwischen den Sprachklassen und eine Hierarchiebeziehung, auch Chomsky Hierarchie genannt.

Diese Sprachen spielen eine große Rolle bei den Programmiersprachen: Typ-2-Sprachen (kontextfrei) erlauben z.B. eine Interpretation von Ausdrücken dieser Sprache, so dass entschieden werden kann ob ein Ausdruck den Regeln der Grammatik entspricht (Parser) oder nicht.

Lernziel 4

Wie definiert man reguläre Mengen?

Im Skript steht, dass jeder Informatiker die regulären Sprachen und ihre Eigenschaften kennen muss. Dem wollen wir uns also nicht verschließen. Die Menge der regulären Sprachen ist die kleinste Sprachklasse in der Chomsky-Hierarchie. Sie sind rechtslinear (der Syntaxbaum neigt sich nach unten rechts weg) und werden von determinierten und nichtdeterminierten Automaten erkannt. Automaten werden leider in der nächsten Kurseinheit besprochen, was ich schade finde. Das würde zum Verständnis dieser KE sicherlich beitragen. Aber sei es drum: wenn euch etwas noch nicht zu 100% klar ist, schaut in die nächste KE.

Aber weiter im Text: Die herausgehobene Position der regulären Sprachen in der Informatik basiert auf deren Verwendung, z.B. als reguläre Ausdrücke in Suchmustern. Bevor wir darauf näher eingehen, definieren wir zunächst die Operationen auf den Sprachen über einem festen Alphabet, die auf Wortmengen zugeschnitten sind:

$X\cdot Y := \{xy\mid x\in X, y\in Y\}$. Komplexprodukt von $X$ und $Y$.

$X^n(n\geq0)$ als $X^0=\{\epsilon\}$ und $X^{n+1}=X^n\cdot X$

$X^{*}=\bigcup_{n\geq 0} X^n$. Sternoperation.

$X^{+}=\bigcup_{n\geq 0} X^n$ ($X^*\cdot X$)

$\overline{X}=\Sigma^{*}\setminus X$ (Komplement bzgl. $\Sigma^{*}$)

$X^{R}=\{x^R\mid x\in X\}$ (Spiegelung)

Definieren wir mal die reguläre Menge/reguläre Sprache wie im Skript:

$\emptyset$ ist eine reguläre Menge über $\Sigma$. Wenn $a$ ein Element von $\Sigma$ ist, so ist die Wortmenge $\{a\}$ eine reguläre Menge über $\Sigma$.

Sind $X$ und $Y$ reguläre Mengen, so ist es auch $X\cup Y, X\cdot Y$ und $Y^{*}$. Die regulären Mengen sind also bzgl. der genannten Operationen abgeschlossen.

Eine Menge nennt man regulär wenn sie in endlich vielen Schritten mit den genannten Operationen in der letzten Definition erzeugt werden kann. Mit $REG_n$ werden im Skript die regulären Mengen über $\Sigma$ genannt, die man in $n$ Schritten erzeugen kann. Da wir bereits die rekursiv aufzählbaren (semi-entscheidbaren) Sprachen hatten, haben die regulären Sprachen einen weiteren Vorteil:

 

Jede reguläre Menge/Sprache ist rekursiv (entscheidbar)

Jede endliche Menge $M\subseteq\Sigma^{*}$ ist regulär

 

Achtung: Damit bilden sie eine echte Teilmenge in den Typ-0-Sprachen (die Menge der rekursiven (entscheidbaren) Sprachen ist eine Teilmenge der rekursiv aufzählbaren Sprachen). Die regulären Sprachen erweisen sich als abgeschlossen unter

• Komplementbildung,
• Konkatenation,
• Schnitt,
• Vereinigung und
• Bildung des Kleeneschen Abschlusses.

Bei Gelegenheit werde ich ein paar Beispiele zu den vorgestellten Operationen in diesen Beitrag einbauen.

Noch ein Nachtrag aus der Wikipedia zum Thema: Möchte man zeigen, dass eine Sprache regulär ist, so muss man sie auf eine reguläre Grammatik, einen endlichen Automaten (z. B. einen Moore-Automaten) oder einen regulären Ausdruck oder auf bereits bekannte reguläre Sprachen zurückführen. Für einen Nachweis, dass eine Sprache  nicht regulär ist, kann man das Pumping-Lemma verwenden (dazu stand leider in dieser KE nichts, aber im Buch von Hoffmann schon. Wenn auch in KE6 und 7 nichts dazu steht, schreibe ich das hier ausführlich hin).

Antwort zum Lernziel: am Anfang stehen die einzelnen Zeichen $a$ unseres Alphabets $\Sigma$. Diese nennen wir regulär. Alles, was wir aus diesen Zeichen mittels Vereinigung, Verkettung und Sternoperation (Kleen'sche Hülle) und der leeren Menge $\emptyset$ (welche der Definition nach ebenfalls regulär ist) basteln können ist ebenfalls regulär.

Haben wir reguläre Mengen $X$ und $Y$, so ist die Menge, die durch die genannten Operationen auf diesen Mengen entsteht... ja, genau: auch regulär.

Lernziel 5

Welche Sprache wird durch einen regulären Ausdruck definiert?

Kommen wir nun zu den regulären Ausdrücken. Mit ihnen können wir reguläre Sprachen beschreiben. Damit kann jede Erzeugungsvorschrift durch einen regulären Ausdruck verschlüsselt werden, so dass wir durch die Syntax (regulärer Ausdruck) die reguläre Sprache (Semantik) bekommen.

Damit ist $L$ unsere Semantikfunktion, die zu jedem regulären Ausdruck $\alpha$ eine Sprache aus $\Sigma^{*}$ zuordnet, sie fungieren als eine Art "Name" für die regulären Mengen (der Satz ist aus dem Skript. Ich finde ihn aber sehr anschaulich und habe ihn deswegen für den Beitrag geklaut).

Definieren wir sie wieder zunächst:

Sei $\Sigma$ ein beliebiges Alphabet, $Reg(\Sigma)$ die Menge der regulären Ausdrücke, die induktiv aus folgenden Regeln gebildet wird:

$\emptyset,\epsilon\in Reg(\Sigma)$

$\Sigma\subset Reg(\Sigma)$

Wenn $r\in{Reg(\Sigma)}$ und $s\in{Reg(\Sigma)}$, dann sind auch $rs$ und $(r\mid s)\in{Reg(\Sigma)}$

Wenn $r\in{Reg(\Sigma)}$, dann sind auch $(r)$ und $r^*\in{Reg(\Sigma)}$

Es gelten die Rechenregeln:

Kommutativgesetz: $r\mid s = s\mid r$

Idempotenzgesetz: $r\mid r = r$

Distributivgesetz: $r(s\mid t) = rs\mid rt$ und $(s\mid t)r=sr\mid tr$

Neutrale Elemente: $r\mid\emptyset =\emptyset\mid r=r$ und $r\epsilon=\epsilon r=r$

Wir können hiermit zu jeder Grammatik einen regulären Ausdruck finden, der die gleiche Sprache erzeugt: eine Sprache aus der Sprachklasse Typ-3. reguläre Ausdrücke und reguläre Grammatiken können auf endliche Automaten reduziert werden.

Wie bereits erwähnt, werden diese regulären Ausdrücke für Suchmuster verwendet. D.h. Werkzeuge wie sed oder grep unter UNIX greifen genau auf dieses Modell zu. Die Konkatenation ($ab$), Auswahl ($a\mid b$) oder der Kleene-Stern ($*$) sind unverändert vorhanden. Alle anderen Erweiterungen dienen der Verkürzung der Schreibweise und lassen sich auf diese Kernkonstrukte zurückführen.

Die Funktion $L$, die unserem regulären Ausdruck $\alpha$ eine Sprache zuordnet wird durch folgende Gleichungen definiert, die wir auch gleich in einem Beispiel anwenden werden:

$L(\emptyset) = \emptyset$

Die vom regulären Ausdruck $\emptyset$ erzeugte Sprache ist leer (es ist das leere Wort $\epsilon$). Nicht vergessen: leere Mengen sind von Definition aus regulär.

$L(a) = \{a\}$

Die vom regulären Ausdruck $a$ erzeugte Sprache ist das Zeichen $a$.

$L(\alpha\cup\beta) = L(\alpha)\cup L(\beta)$

Die Sprache, die aus der Vereinigung von zwei regulären Ausdrücken $\alpha$ und $\beta$ beschrieben wird, kann man auch auch durch die Vereinigung der Sprachen, die nur durch $\alpha$ und $\beta$ beschrieben werden, erzeugen.

$L(\alpha\beta) = L(\alpha)\cdot L(\beta)$

Die Sprache, die aus der Konkatenation von zwei regulären Ausdrücken $\alpha$ und $\beta$ beschrieben wird, kann man auch auch durch die Konkatenation der Sprachen, die nur durch $\alpha$ und $\beta$ beschrieben werden erzeugen.

$L(\alpha^{*}) = (L(\alpha))^{*}$

Die Sprache, die durch den Sternoperator, angewandt auf den regulären Ausdruck $\alpha$ erzeugt wird, kann auch durch Anwendung des Sternoperators auf die nur durch $\alpha$ beschriebene Sprache erzeugt werden.

Am einfachsten zeigt man die Anwendung sicher an einem kleinen Beispiel (aus dem Skript).

Beispiel: regulärer Ausdruck $\beta=(\emptyset^{*}\cup(a^{*}b))$

Wir suchen also die durch den Ausdruck beschriebene Sprache $L(\beta)$. Das geht ganz simpel durch Auflösen:

$\begin{align}L(\beta)&=L((\emptyset^{*}\cup(a^{*}b)))\\&=L(\emptyset^{*})\cup L(a^{*}b)\\&=L(\emptyset^{*})\cup(L(a^{*})\cdot\{b\})\\&=\{\epsilon\}\cup(\{a\}^{*}\cdot\{b\})\\&=\{\epsilon\}\cup\{a\}^{*}\cdot\{b\}\end{align}$

Damit ist die zum regulären Ausdruck $\beta$ gesuchte Sprache $L(\beta)=\{\epsilon\}\cup\{a\}^{*}\cdot\{b\}$.

Was haben wir gemacht?

$(1)$ Auflösung von $\beta$

$(2)$ wir können nicht nur Elemente, sondern auch Mengen mit den oben genannten Operationen verbinden, was wir hier der Übersichtlichkeit halber getan haben.

$(3)$ $\{b\}$ ist nur ein einzelnes Zeichen, dass können wir ebenfalls für die Übersichtlichkeit rausnehmen und mit der Konkatenation wieder verbinden

$(4)$ welche Sprache beschreibt $L(\emptyset)$? Keine große, es besteht nur aus dem leeren Wort $\epsilon$. Gesagt, getan! Was beschreibt $L(a^*)$? Nur einen beliebig langen String aus $a's$. Also auflösen.

$(5)$ und nun das Verbliebene nur noch mit den Operatoren verbinden und wir haben unsere Sprache gefunden.

Antwort zum Lernziel: mit regulären Ausdrücken (d.h. die Verwendung von Zeichen aus dem Alphabet mit den auf regulären Mengen definierten Operationen Vereinigung, Konkatenation und Kleene Stern) beschreiben wir Erzeugungsvorschriften für reguläre Sprachen. Sie fungierten so als eine Art "Name" für eine reguläre Menge.

Lernziel 6

Was ist eine rechtslineare Grammatik?

Wie wir oben bereits geschrieben haben ist jede reguläre Grammatik auch eine rechtslineare Grammatik. Aufgrund der Struktur der Produktion neigt sich der Syntaxbaum nach rechts unten weg. Die Regeln haben folgende Form:

$A\rightarrow\omega B$ oder

$A\rightarrow\omega$

Das heißt soviel, dass die rechte Seite der Produktion aus einem Wort (mehrere Zeichen) über $\Sigma$ und einem Nonterminal oder nur einem Wort über $\Sigma$ besteht. Merkt euch die Definition, der Unterschied zur rechtslinearen Normalformgrammatik ist nur ganz klein, aber wichtig. Mit dem leeren Wort $\epsilon$ können wir ein Nonterminal verschwinden lassen und so den Ableitungsprozess stoppen.

Ein Beispiel aus dem Buch von Dirk. W. Hoffmann (auf die Definition Skript gemünzt): $G_1=(\Pi,\Sigma,R,S)$ mit $\Pi=\{S,B,C\}$, $\Sigma=\{a,b\}$, Startsymbol $S$ und den Regeln $R$:

$S\rightarrow aB$

$B\rightarrow bC$

$C\rightarrow\epsilon\mid aB$

Wollen wir z.B. $abab$ ableiten, also schauen ob $abab\in L(G_1)$ ist, so haben wir folgende Sequenz: $S\rightarrow aB\rightarrow abC\rightarrow abaB\rightarrow ababC\rightarrow abab$. Der Syntaxbaum hierzu sieht wie folgt aus:

Schaut nochmal zur Definition der Typ-3-Sprachen (erzeugt von regulären Grammatiken, damit ist jede reguläre Sprache auch rechtslinear) hoch. Unsere Grammatik $G_1$ erfüllt genau die dort gemachten Einschränkungen und erzeugt unsere Sprache. Sie ist außerdem auch noch in einer (rechtslinearen) Normalform, aber dazu gleich mehr.

Antwort zum Lernziel: eine rechtslineare Grammatik hat eine bestimmte Form der Produktionsregeln (auf der rechten Seite der Produktion steht entweder ein Wort oder ein Wort, gefolgt von einem Nonterminal). Da nur am äußersten, rechten Rand ein Nonterminal steht, dass ersetzt werden kann, neigt sich der Ableitungsbaum nach rechts.

Diese Regeln entsprechen denen für die Typ-3 Grammatiken, so dass jede reguläre Sprache auch rechtslinear ist.

Lernziel 7

Wie zeigt man, dass die reguläre Sprache von rechtslinearen Grammatiken erzeugt wird?

Eine von einer regulären Grammatik erzeugte Sprache nennt man reguläre Sprache. Für jede reguläre Sprache existiert auch immer mindestens eine reguläre Grammatik. Wir müssen also zeigen, dass wir aus einer rechtslinearen Grammatik mit den bei Typ-3-Definition gemachten Einschränkungen eine reguläre Sprache erzeugen können.

Die Beweisidee im Skript folgt der Induktion über den Aufbau regulärer Mengen mittels der Operationen Vereinigung, Produkt und Stern aus den Mengen $\emptyset$ und $\{a\}$ über einem Alphabet $\Sigma$. Es wird gezeigt, dass es zu diesen Mengen rechtslineare Grammatiken gibt. Wenn das der Fall ist, so gibt es auch (aufgrund der Abgeschlossenheit) auch rechtslineare Grammatiken zu den Ergebnissen wenn man Vereinigung, Produkt und Stern auf $\emptyset$ und $\{a\}$ anwendet.

Ohne auf Details einzugehen:

1. Wir zeigen, dass wir die Sprachen $L_1=\emptyset$ und $L_2=\{a\}$ durch entsprechende Grammatiken $G_1$ und $G_2$ erzeugen können

2. Anschließend zeigen wir, dass wir durch die Vereinigung $L_1\cup{L_2}$ eine neue Sprache $L$ bekommen, die wir wiederum durch eine entsprechende Grammatik $G$ erzeugen können

3. Nun kümmern wir uns um das Produkt $L_1\cdot{L_2}$ und zeigen ebenfalls, dass wir zu der erzeugten Sprache $L$ eine Grammatik $G$ angeben können, die $G$ erzeugt

4. Und als letztes das Gleiche mit dem Sternoperator: $L={L_1}^{*}$

Damit erzeugen rechtslineare Grammatiken mindestens alle regulären Sprachen.

Antwort zum Lernziel: mittels der Operationen Kleene Stern, Vereinigung und Konkatenation können wir aus den Mengen $\emptyset$ und $\{a\}$ weitere reguläre Mengen erzeugen. Diese werden anschließend mittels passender Grammatik, die den "rechtslinearen Einschränkungen" unterliegt erzeugt.

Da wir mit den drei Operationen alle regulären Mengen abbilden können und für alle dadurch erzeugten, neuen Mengen rechtslineare Grammatiken angegeben haben, können wir so sagen, dass alle regulären Sprachen von rechtslinearen Grammatiken erzeugt werden.

Lernziel 8

Wie transformiert man eine rechtslineare Grammatik in eine rechtslineare Normalform?

Zunächst: was ist eine Normalform? Im Prinzip ist es eine Vereinfachung durch Umformung. In einer rechtslinearen Normalformgrammatik haben alle Regeln die Form:

$A\rightarrow aB$ oder

$A\rightarrow\epsilon$

D.h. dass einem Terminalsymbol (kann nicht weiter ersetzt werden, hier $a$) immer ein Nonterminalsymbol (kann weiter ersetzt werden, hier $A$ und $B$) folgt. Die Nonterminale können also nur ersetzt werden durch ein leeres Wort $\epsilon$ oder durch die Kombination eines Terminalsymbols mit einem Nonterminalsymbol.

Und jetzt schaut einmal kurz hoch zur Definition der rechtslinearen Grammatik: ist euch der Unterschied aufgefallen? Anstatt, dass die rechte Seite der Produktion auch Wort $\omega$ erlaubt, erlaubt uns die Normalform nur ein einziges Terminalzeichen, d.h. nur noch ein Symbol $a$ auf rechten Seite. Damit werden alle Wörter in regulären Grammatiken in Normalform immer nach dem selben Prinzip erzeugt: ausgehend vom Startsymbol wird jede Produktion immer ein Zeichen anfügen und ein Nichtterminal ersetzen. Wir verlängern die Zeichenkette in einem Ableitungsschritt immer nur um ein Zeichen und begrenzen es durch ein immer wechselndes Nonterminal.

Um also eine rechtslineare Grammatik in eine rechtslineare Normalform zu transformieren werden die Terminalregeln so angepasst, dass die Grammatik terminiert, die Regeln verkürzt und so alle Regeln eliminiert, die nicht der Normalform entsprechen (d.h. es kommt keine Regel der Forml $A\rightarrow B$ (Nonterminal zu Nonterminal, Platzhalter zu Platzhalter) vor).

Und jetzt kommt der Grund, warum ich die Kurseinheit 5 so gerne mag: ein sehr ausführliches Beispiel dieser einer Transformation, dass ich hier auch gerne ausführen würde:

Beispiel: $G=(\Pi,\Sigma,R,S)$ mit

$\Pi=\{S,A,B,C\}$ (unsere Nonterminale)

$\Sigma=\{a,b\}$ (unsere Terminale)

und folgenden Regeln $R$:

$S\rightarrow A$

$S\rightarrow B$

$A\rightarrow C$

$A\rightarrow aB$

$A\rightarrow baaB$

$B\rightarrow A$

$B\rightarrow bbC$

$C\rightarrow a$

Man sieht gleich, dass das wir hier einige Regeln haben, die nicht der Normalform entsprechen. Die müssen wir nun loswerden.

1. Der Übersicht halber wird mit $\mid$ abgekürzt:

$S\rightarrow A\mid B$

$A\rightarrow C\mid aB\mid baaB$

$B\rightarrow A\mid bbC$

$C\rightarrow a$

2. Nun kümmern wir uns um die korrekte Terminierung, d.h. $G$ muss die Möglichkeit bieten ein Nichtterminal durch ein leeres Wort  $\epsilon$ zu ersetzen. Wie man sieht, ist das bei unseren Regeln nicht der Fall. Wir fügen also eine neue Regel ein und passen die letzte Regel an damit die Terminierung auch erreichbar ist:

$S\rightarrow A\mid B$

$A\rightarrow C\mid aB\mid baaB$

$B\rightarrow A\mid bbC$

$C\rightarrow aE$

$E\rightarrow\epsilon$

3. Nun werden die Regellängen verkürzt. Wir haben einige Regeln, die bestehen aus mehr Terminalen als für die Normalform notwendig. Wir verkürzen also die Regeln $A\rightarrow baaB$ und $B\rightarrow bbC$ in jedem Schritt um ein Terminalsymbol indem wir ein neues Nonterminal einführen. Das wird solange fortgeführt bis wir in unserer Normalform landen:

$A\rightarrow baaB$ wird zu

$A\rightarrow bX$ und

$X\rightarrow aaB$

Letzteres wird dann weiter transformiert zu

$X\rightarrow aY$ und

$Y\rightarrow aB$

Länge erreicht. Das Gleiche wird mit $B\rightarrow bbC$ durchgeführt und wir kommen insg. zu:

$S\rightarrow A\mid B$

$A\rightarrow C\mid aB\mid bX$

$X\rightarrow aY$

$Y\rightarrow aB$

$B\rightarrow A\mid bZ$

$Z\rightarrow bC$

$C\rightarrow aE$

$E\rightarrow\epsilon$

4. Jetzt werden nur noch die Regeln eliminiert, die auf Nonterminale zeigen (d.h. in der Form $S\rightarrow A$). Dazu ersetzen wir einfach das zu eliminierende Nonterminal durch seine "Ersatzzeichenkette". Auf der rechten Seite der Produktionen haben wir die Nonterminale $A,B$ und $C$, die wir ersetzen müssen. Wir fangen zunächst mit $A$ an und ersetzen es durch seine "Ersatzzeichenkette" $C\mid aB\mid bX$ in den Regeln $S$ und $B$.

$S\rightarrow C\mid aB\mid bX\mid B$

$A\rightarrow C\mid aB\mid bX$

$X\rightarrow aY$

$Y\rightarrow aB$

$B\rightarrow C\mid aB\mid bX\mid bZ$

$Z\rightarrow bC$

$C\rightarrow aE$

$E\rightarrow\epsilon$

Nun kümmern wir uns um $B$ und ersetzen es durch seine "Ersatzzeichenkette" $C\mid aB\mid bX\mid bZ$ in seinem einzigen Vorkommen in $S$:

$S\rightarrow{C\mid aB\mid bX\mid C\mid bZ}$

$A\rightarrow C\mid aB\mid bX$

$X\rightarrow aY$

$Y\rightarrow aB$

$B\rightarrow{C\mid aB\mid bX\mid bZ}$

$Z\rightarrow bC$

$C\rightarrow aE$

$E\rightarrow\epsilon$

Fehlt nur noch $C$, dass überall auf der rechten Seite der Produktionen durch $aE$ ersetzt wird und wir haben am Ende eine rechtslineare Normalform:

$S\rightarrow aE\mid aB\mid bX\mid bZ$

$A\rightarrow aE\mid aB\mid bX$

$X\rightarrow aY$

$Y\rightarrow aB$

$B\rightarrow aE\mid aB\mid bX\mid bZ$

$Z\rightarrow bC$

$C\rightarrow aE$

$E\rightarrow\epsilon$

Antwort zum Lernziel: bei einer rechtslinearen Grammatik gilt nur die Einschränkungen $A\rightarrow\omega B$ oder $A\rightarrow\omega$. D.h. die rechte Seite der Produktion muss aus einem Wort, welches mit einem Nonterminal abschließt oder nur durch ein Wort bestehen. Bei der zugehörigen Normalform ist das nicht mehr erlaubt. Dort gelten nur noch die Regeln $A\rightarrow aB$ sowie die Abschlussregel $B\rightarrow\epsilon$.

Durch Verkürzung der Produktionen, eine korrekte Terminierung mit $\epsilon$, Eliminierung der Regeln, die nicht dem genannten Schema für die Normalform entsprechen können wir so eine rechtslineare Grammatik in eine Normalform überführen.

Und das war auch schon KE5. Wie immer gilt: Wer Fehler oder Ungenauigkeiten findet, ab in die Kommentare oder per Mail.

 

Datum: 23. Mai 2013
Kategorie: Theoretische Informatik
Kommentarfeed: RSS 2.0 • Trackback: Trackback-Url

Sie können zum Ende springen und ein Kommentar hinterlassen. Pingen ist im Augenblick nicht erlaubt.