Vorletzte Kurseinheit. Und dazu noch ein eig. sehr schönes Thema. Die letzte KE und diese hier gehören ganz eng zusammen; ich kämpfe noch mit mir nicht einen einzigen Eintrag aus beiden Kurseinheiten zu gießen. Ich empfehle euch beide in einem Tab/Fenster aufzumachen damit Ihr beide Einträge vor der Nase habt und zwischen ihnen blättern könnt wenn in diesem Eintrag auf Sätze aus KE5 Bezug genommen wird.
Leider sind die letzten Kurseinheiten etwas dicker 😉 Kämpfen wir uns also wieder direkt durch die Lernziele.
Lernziel 1
Wie definiert man die von einem endlichen Automaten erkannte Sprache?
In dieser Kurseinheit sind Turingmaschinen mit einem Einweg-Ausgabeband ohne Arbeitsbänder im Fokus. Auch wenn man sie als Turingmaschinen notieren kann, wird eine andere Notation verwendet. Die der endlichen Automaten. Starten wir mit der Definition und einem Beispiel:
Endlicher (nichtdeterministischer) Automat
Quintupel \(A=(\Sigma,Q,q_0,F,\delta)\) mit
\(\Sigma\) als Eingabealphabet
\(Q\) als endliche Menge der Zustände
\(q_0\in Q\) als Anfangszustand
\(F\subseteq Q\) als Menge der Endzustände
\(\delta\subseteq Q\times\Sigma\times Q\) als Überführungsrelation
Dieser Teil der Definition macht euch sicher kaum Probleme, haben wir doch bereits Turingmaschinen in ähnlicher Weise definiert. Die Überführungsrelation führt einfach nur von einem Zustand aus \(Q\) zu einem anderen Zustand aus \(Q\) bei der Eingabe von einem Element aus dem Eingabealphabet \(\Sigma\).
Nun definieren wir noch \(\delta\):
\(\delta^0=\{(q,\epsilon,q)\mid q\in{Q}\}\) \(\delta^{n+1}=\{(p,xa,q)\mid x\in{\Sigma}^{*},a\in{\Sigma},\exists r\in{Q}.(p,x,r)\in\delta^{n}\wedge(r,a,q)\in\delta\}\)\(\delta^{*} = \bigcup_{n\geq 0}\delta^n\) ist die transitive Hülle von \(\delta\)
Oha. Die induktive Definition der Überführungsrelation ist nicht so einfach. Aber warten wir das folgende Beispiel gleich ab, dann wird es klarer. In der transitiven Hülle sind auch indirekte Relationen drin, d.h. erreichen wir z.B. den Zustand \(q_2\) bei der Eingabe von \(a\) nur über \(q_1\) ausgehend vom Startzustand \(q_0\), so hätten wir eig. nur die Relationen \((q_0,a,q_1)\) und \((q_1,a,q_2)\). In der transitiven Hülle \(\delta^{*}\) haben wir jedoch auch noch das indirekte Tripel \((q_0,a,q_2)\) drin.
Diese Tripel in \(\delta^{*}\) können nicht nur einzelne Zeichen aus \(\Sigma\) beinhalten, sondern können der Definition nach auch Worte sein. Führt uns z.B. die Eingabe \(aaabbb\) zu einem Endzustand, so ist in der transitiven Hülle \(\delta^{*}\) auch \((q_0,aaabbb,q)\) drin (wobei \(q_0\) ein Anfangs- und \(q\) ein Endzustand ist). Wird gleich im folgenden beispiel etwas verständlicher, versprochen.
Kommen wir nun zur akzeptierten Sprache \(L(A)\):
\(L(A):=\{x\in\Sigma^{*}\mid\exists q\in F.(q_0,x,q)\in\delta^{*}\}\) \(L(A):=\{x\in\Sigma^{*}\mid\delta^{*}\cap(\{q_0\}\times\{x\}\times F)\neq\emptyset\}\)
Es gilt also \(x\in L(A)\) genau dann wenn \(x\) den Anfangszustand in einen Endzustand überführt. Damit ist genau das die von dem endlichen Automaten \(A\) erkannte Sprache \(L(A)\). Nun kümmern wir uns um die Worte determiniert und vollständig.
determiniert, gdw. \(\#\{q\in Q\mid(p,a,q)\in\delta\}\leq 1\) für alle \(p\in Q,a\in\Sigma\)
vollständig, gdw. \(\#\{q\in Q\mid(p,a,q)\in\delta\}\geq 1\) für alle \(p\in Q,a\in\Sigma\)
Gar nicht so schwer: determiniert bedeutet, dass wir ausgehend vom Startzustand \(q_0\) das Wort \(x\) von links nach rechts ableiten und immer einen Folgezustand haben. Wenn es mal keinen Folgezustand gibt, so ist der Automat nicht vollständig und es gilt \(x\notin L(A)\). Gibt es einen Zustand \(p_n\) für die Eingabe \(x\), wobei \(n=lg(x)\) (Länge von \(x\)), so gilt: \(x\in L(A)\Leftrightarrow p_n\in F\). D.h. soviel wie wenn die Länge von \(x\) \(n\) ist, so muss nach \(n\) Schritten der Endzustand \(p_n\) erreicht worden sein. Damit ist dann auch \(x\in L(A)\). Landet man nach \(n\) Berechnungsschritten nicht im Endzustand, so ist \(x\notin L(A)\).
Nichtdeterminierte Automaten sind – genauso wie \(NTM\) – reine Gedankenmodelle. Hierzu gibt es ein Beispiel im Skript, dass ich auch gerne anführen würde:
Beispiel: \(A=(\Sigma,Q,q_0,F,\delta)\) mit
\(\Sigma=\{a,b\}\) (Eingabealphabet)
\(Q=\{0,1,2\}\) (Zustände)
\(q_0=0\) (Startzustand)
\(F=\{2\}\) (Endzustand)
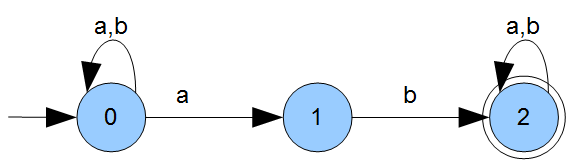
\(\delta=\{(0,a,0),(0,b,0),(0,a,1),(1,b,2),(2,a,2),(2,b,2)\}\)
Wir zeichnen die Zustände als Kreise, weisen Start- und Endzustand entsprechend aus und jeder Übergang von einem Zustand zum anderen wird eine gerichtete und gekennzeichnete Kante zwischen diesen. Gibt es bereits einen Übergang, so müssen wir die Kante mit dem zusätzlichen Zeichen nur noch kennzeichnen.
Dieser ist nicht determiniert. Warum? Weil es für für eine Eingabe und einen Zustand zwei Folgezustände gibt: \((0,a,1)\) und \((0,a,0)\).
Auch ist er nicht vollständig: Warum? Weil wir im Zustand \(1\) für die Eingabe \(a\) keinen Folgezustand haben.
Wie sieht unsere transitive Hülle \(\delta^{*}\) aus? Sie hat z.B. auch noch zusätzlich das indirekten Tripel \((0,b,2)\) drin. Und was ist mit dem \(\delta^n\)? Dazu kommen wir auch gleich. Ersteinmal stellen wir uns die Frage: Welche Sprache entscheidet der Automat?
Zunächst einmal können wir eine absolut beliebige Kombination aus \(a\) und \(b\) haben und verweilen im Zustand \(0\): \({\{a,b\}}^{*}\). Erst wenn wir zum Zustand \(2\) wollen, benötigen wir als Abschluss des ersten Teils der Zeichenkette ein \(\{ab\}\). Und dort angekommen sind wir entweder fertig oder können im Zustand \(2\) so verweilen, wie wir auch in Zustand \(0\) verweilt haben: mit einer beliebigen Kombination aus \(1\) und \(b\): \({\{a,b\}}^{*}\).
Damit ist die von \(A\) erkannte Sprache \(L\), d.h. \(L(A)={\{a,b\}}^{*}\{ab\}{\{a,b\}}^{*}\)
Und nun kümmern wir uns um \(\delta^n\) am versprochenen Beispiel (ebenfalls aus dem Skript geklaut).
Beispiel \(a^4b^2\in L(A)\)?
Wir müssen also schauen ob die Eingabe \(x=aaaabb\) uns zu einem Endzustand (ein Zustand aus \(F\)) bringt oder nicht. In jedem Schritt bringt uns ein Zeichen aus dem Wort zu einem Folgezustand. Und wenn es mal keinen gibt oder wir nach \(lg(x)=6\) Schritten noch keinen Endzustand erreicht haben, so ist das Wort nicht Teil unserer Sprache \(L(A)\). Versuchen wir es also:
\((0,\epsilon,0)\in\delta^0\)
\((0,a,0)\in\delta^1\) da \((0,a,0)\in\delta\)
\((0,aa,0)\in\delta^2\) da \((0,a,0)\in\delta\)
\((0,aaaa,0)\in\delta^3\) da \((0,a,0)\in\delta\)
\((0,aaaaa,1)\in\delta^4\) da \((0,a,1)\in\delta\)
\((0,aaaab,2)\in\delta^5\) da \((1,b,2)\in\delta\)
\((0,aaaabb,2)\in\delta^6\) da \((2,b,2)\in\delta\)
Wir sehen also, dass wir Ausgehend vom Startzustand \(0\) zum Zustand \(2\) gelangen, welcher ein Endzustand ist. Es liegt daher \((0,aaaabb,2)\in\delta^{*}\), woraus folgt, dass \(a^4b^2\in L(A)\)! Um zu zeigen, dass ein Wort zur Sprache gehört, müssen wir also einfach nur eine Zustandsfolge angeben, die die zu prüfende Eingabe in den Endzustand überführt. Braucht Ihr noch ein Beispiel um zu zeigen, dass eine Zeichenfolge nicht in \(L(A)\) ist? Gerne.
Beispiel: \(a^4\in L(A)\)?
Spielen wir den Graphen mit der Eingabe \(aaaa\) durch, so sehen wir, dass wir nie in im Endzustand \(2\) landen. Wir bleiben immer nur in \(0\) oder \(1\). Damit ist \(a^4\notin L(A)\)? Probiert die nächsten beiden mal selbst.
Übung: \(a^2 b^2\in L(A)\) \((aabb)\)?
Übung: \((ba)^3\in L(A)\) \((bababa)\)?
Übung: \((ba)\in L(A)\) \((ba)\)?
Antwort zum Lernziel: Damit ist die von einem endlichen Automaten \(A\) erkannte Sprache \(L\) die Menge der Worte über dem Alphabet \(\Sigma\), die ausgehend von einem Startzustand \(q_0\) den Automaten in einen Endzustand \(q\) überführt und dabei nicht mehr Berechnungsschritte braucht als die Eingabe lang ist.
Lernziel 2
Wie kann man zu einem nichtdeterminierten endlichen Automaten einen determinierten konstruieren, der dieselbe Sprache erkennt?
Im Beitrag zu KE5 haben wir es bereits angedeutet: die Regeln aus den Grammatiken sind nichts weiter als Überführungsrelationen in Maschinen von einem Zustand zum anderen. Aus diesem Grund können wir rechtslineare Normalformgrammatiken in Automaten überführen. Dazu brauchen wir folgendes:
Transformation \(T\) mit \(T((\Pi,\Sigma,R,S)):=(\Sigma,\Pi,S,F,\delta)\) mit
\(F=\{A\in\Pi\mid (A\rightarrow\epsilon)\in R\}\) und
\(\delta=\{(A,a,B)\in\Pi\times\Sigma\times\Pi\mid (A\rightarrow aB)\in R\}\)
Wir transformieren damit eine rechtslineare Normalformgrammatik in einen Automaten, so dass \(L(G)=L(T(G))\) gilt. Die Definition von \(F\) (unseren Endzuständen im Automaten) besagt lediglich, dass in die Menge der Endzustände unseres Automaten das Nonterminal reingehört. was auch als Regel für ein Nonterminal in den Regeln der Grammatik vorhanden ist und auf \(\epsilon\) zeigt.
Mit \(\delta\) ist es ähnlich. In die Überführungsrelationen gehören alle Regeln rein, die auf ein Terminal (unsere Eingabe im Automaten) und ein Nonterminal (unser Zustand im Automaten) zeigen. Das ist dann unser Zustandsübergang. Am besten ein Beispiel, oder? Nehmen wir dazu doch einfach die Grammatik, die wir im vorherigen Beitrag verwendet haben.
Beispiel: \(G_1=(\Pi,\Sigma,R,S)\) mit \(\Pi=\{S,B,C\}\), \(\Sigma=\{a,b\}\), Startsymbol \(S\) und den Regeln \(R\):
\(S\rightarrow aB\)
\(B\rightarrow bC\)
\(C\rightarrow\epsilon\mid aB\)
Wir müssen also aus der rechtslinearen Normalformgrammatik \(G_1\) einen endlichen Automaten basteln. Weder am Alphabet \(\Sigma\), noch an den Zuständen (Nonterminalen) \(\Pi\) oder am Startzustand \(S\) haben wir was zu kamellen. Wir brauchen die Menge der Endzustände \(F\) und unsere Überführungsrelationen \(\delta\).
Fangen wir mit dem Endzustand \(F\) an. Schaut noch einmal die Definition von \(F\) oben an. Wir suchen also in den Regeln \(R\) unserer Grammatik \(G_1\) nach der Regel von der Form \((A\rightarrow\epsilon)\). Die einzige Regel, die so aussieht ist die Regel für \(C\rightarrow\epsilon\mid aB\). Damit haben wir den Endzustand der Grammatik \(C\) nun in unserer Automaten-Menge \(F\). Hätten wir mehr Regeln, die auf ein \(\epsilon\) zeigen, so hätten wir auch mehr Endzustände.
Jetzt die Überführungsrelationen \(\delta\): wir transformieren alle Regeln der Grammatik mit der Form \((A\rightarrow aB)\) in die Überführungsrelation für dem Automaten mit der Form \((A,a,B)\):
\(S\rightarrow aB\Rightarrow(S,a,B)\)
\(B\rightarrow bC\Rightarrow(B,b,C)\)
\(C\rightarrow aB\Rightarrow(C,a,B)\)
That’s it. Wie sieht der Automat nun aus? So:
Fertig! Wir sehen auch hier, dass er nicht vollständig ist: es fehlt im Zustand \(S\) der Folgezustand für die Eingabe eines \(b\). Aber er ist determiniert, da wir nicht mehrere Folgezustände für eine Eingabe haben.
Nachdem das nun geklärt ist, kümmern wir uns um die Überführung von nichtdeterminierten Automaten in determinierte. Der Vorteil von letzteren liegt darin, dass diese sich mittels Boole’schen Schaltwerken realisieren lassen. Wäre doch schön wenn wir dazu die nichtdeterminierten Automaten in determinierte überführen könnten…
Beispiel: der Automat aus dem ersten Beispiel mit \(A=(\Sigma,Q,q_0,F,\delta)\) mit
\(\Sigma=\{a,b\}\) (Eingabealphabet)
\(Q=\{0,1,2\}\) (Zustände)
\(q_0=0\) (Startzustand)
\(F=\{2\}\) (Endzustand)
\(\delta=\{(0,a,0),(0,b,0),(0,a,1),(1,b,2),(2,a,2),(2,b,2)\}\)
und dem zugehörogen Graphen
Die Menge der neuen Zustände ist maximal \(2^Q = 2^3 = 8\). Wobei wir nicht alle benötigen werden. Dazu stellen wir eine Tabelle auf, die uns am Ende zeigt welche Übergänge und welche Zustände wir haben. Wir fangen einfach mal an, die Inhalte der Spalten erschließen sich dann direkt:
| V | W | W\V | |
| P | a | b | |
| {0} | {0,1} | {0} | {0,1} |
In der ersten Zeile, in Spalte \(P\) steht der Startzustand. In Spalte \(a\) und \(b\) stehen die jeweils erreichbaren Zustände bei der jeweiligen Eingabe, ausgehend vom Zustand in Spalte \(P\). D.h. ausgehend von Startzustand \(0\) erreichen wir bei der Eingabe von \(a\) Folgezustand \(0\) und \(1\) und bei der Eingabe von \(b\) nur Zustand \(0\). In der Spalte \(W\setminus{V}\) befindet sich die Elemente der Menge \(W=\{\{0,1\},\{0\}\}\) ohne die Elemente der Menge \(V=\{\{0\}\}\), also nur \(W\setminus{V}=\{\{0,1\}\}\). Damit haben wir die erste Zeile aufgebaut.
Für die Spalte \(P\) in der zweite Zeile nehmen wir ein Element aus der Menge \(W\setminus{V}=\{\{0,1\}\}\). Viel Auswahl haben wir hier nicht (hätten wir eine, so wäre die Auswahl willkürlich, sie würde nur die Reihenfolge der Zeilen beeinflussen). Nun werden wieder die erreichbaren Folgezustände, ausgehend von Startzustand \(0\) und \(1\) bei der Eingabe von \(a\) und \(b\) in den folgenden Spalten notiert und in der letzten Spalte wieder \(W\setminus{V}\) eingetragen. Das machen wir solange, bis die Menge \(W\setminus{V}\) leer (\(W\setminus{V}=\emptyset\)) ist. Am Ende haben wir die folgende Tabelle:
| V | W | W\V | |
| P | a | b | |
| {0} | {0,1} | {0} | {0,1} |
| {0,1} | {0,1} | {0,2} | {0,2} |
| {0,2} | {0,1,2} | {0,2} | {0,1,2} |
| {0,1,2} | {0,1,2} | {0,2} | |
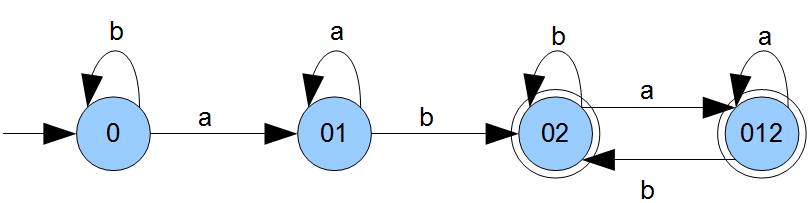
Aus dieser können wir nun alle notwendigen Zustände (Spalte \(P\)) und die Folgezustände (Spalten \(a\) und \(b\)) ableiten. Alle Zustände aus Spalte \(P\), die die Zahl eines Endzustandes (\(2\)) des ursprünglichen Automaten beinhalten, werden ebenfalls zu Endzuständen. Am Ende kommt daher folgender Graph raus:
Wenn wir die Wertetabelle dazu aufstellen sehen wir auch, dass wir einen Zustand wegkürzen können (wie in Computersysteme 1 und 2).
| Zustand | Folgezustand bei Eingabe von „a“ | Folgezustand bei Eingabe von „b“ |
| 0 | 01 | 0 |
| 01 | 01 | 02 |
| 02 | 012 | 02 |
| 012 | 012 | 02 |
Zustand \(02\) und \(012\) sind äquivalent und damit kürzbar (wenn man zur \(b\)-Kante von \(02\) noch \(a\) hinzufügt).
Antwort zum Lernziel: zu einem nichtdeterminierten Automaten kann man einen determinierten Automaten konstruieren, der dieselbe Sprache erkennt, indem man eine neue Zustandsmenge definiert, die maximal aus der Potenzmenge \(2^Q\) der ursprünglichen Zustände \(Q\) führt. Die Menge der benötigten Zustände ergibt sich aus allen erreichbaren Zuständen.
Diese neuen Automaten werden Potenzautomaten genannt. Damit lässt sich festhalten, dass man zu jedem endlichen, nicht-deterministischen Automaten einen deterministischen Automaten angeben kann, der die selbe Sprache erkennt.
Da die Namen der neuen Zustände aus den Namen der Ursprungszustände bestehen, können die gerichteten Kanten auch zu den neuen Zuständen problemlos gezogen und so die Zustandsübergänge im neuen Graphen modelliert werden. Durch die Benennung lassen sich auch die Endzustände im neuen, deterministischen Graphen identifizieren: jeder neue Zustand, der in seinem neuen Namen den Namen eines ursprünglichen Endzustands beinhaltet, wird ebenfalls ein Endzustand.
Das war der erste Teil von KE6. Wer Fehler findet: ab in die Kommentare.