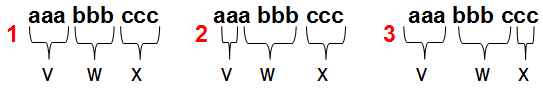Update: Flüchtigkeitsfehler rausgenommen.
Das ist nun die letzte Kurseinheit der theoretischen Informatik B. Traurig? 😉
In dieser Kurseinheit geht es um kontextfreie Sprachen (also Sprachen, die Typ-2 und -3 erzeugen). Am besten man betrachtet die letzten drei Kurseinheiten gemeinsam, ggf. erstelle ich eine kleine Zusammenfassung der Kernaussagen bei Gelegenheit um aus den Puzzleteilen wenigstens teilweise ein Gesamtbild zu bekommen.
Lernziel 1
Wann ist eine Grammatik in Chomsky-Normalform und wie konstruiert man eine solche aus einer beliebigen kontextfreien Grammatik?
Zunächst geht es um die Eliminierung von \(\epsilon\)-Regeln. Unserem leeren Wort, welches als Abschluss einer Ableitung fungiert, indem man ein Nonterminal durch \(\epsilon\) ersetzt. D.h. was wir wollen, ist es die \(\epsilon\)-Regeln (z.B. \(A\rightarrow\epsilon\)) loszuwerden um eine „effektive“ Notation zu bekommen. Aber der Reihe nach:
Chomsky Normalform:
Eine Chomsky Normalform liegt dann vor, wenn alle Regeln/Produktionen die Form \((A\rightarrow a)\) oder \((A\rightarrow BC)\) besitzen mit \(A,B,C\in\Pi\) und \(a\in\Sigma\).
D.h. wir dürfen hier keine \(\epsilon\)-Regeln haben und die rechte Seite der Produktion darf entweder nur aus einem Symbol (noch aus mehreren) aus unserem Alphabet oder aus einer Kombination von maximal zwei Nonterminalen bestehen.
Die Frage ist: wie kommen wir von einer kontextfreien Grammatik zu einer in Chomsky Normalform? Ich finde, dass so etwas am besten an einem Beispiel (aus dem Buch von Dirk W. Hoffmann) gezeigt wird.
Beispiel: Grammatik \(G\) mit Regelmenge
\(S\rightarrow AB\)
\(S\rightarrow ABA\)
\(A\rightarrow aA\)
\(A\rightarrow a\)
\(B\rightarrow Bb\)
\(B\rightarrow\epsilon\)
1. Elimination der \(\epsilon\)-Regeln
Hier entfernen wir zunächst alle Regeln der Form \(A\rightarrow\epsilon\). Wir man sehen kann, wird das Nonterminal \(B\) in unseren regeln durch \(\epsilon\) ersetzt. Diese Ersetzung können wir durch Hinzufügen neuer Regeln „vorwegnehmen“.
\(S\rightarrow AB\)
\(S\rightarrow A\)
\(S\rightarrow ABA\)
\(S\rightarrow AA\)
\(A\rightarrow aA\)
\(A\rightarrow a\)
\(B\rightarrow Bb\)
\(B\rightarrow b\)
Hätten wir z.B. mit der initialen Regelmenge die Ableitungssequenz \(S\Rightarrow ABA\Rightarrow AA\) (Regel 2, Regel 6), so haben wir nun nur noch die Sequenz: \(S\Rightarrow AA\) (Regel 4). Die Ersetzung von \(B\) durch \(\epsilon\) wurde durch neue Regeln obsolet und wir sind der Chomsky Normalform, wo eben \(\epsilon\) kein Teil der Sprache ist, ein Schritt näher.
2. Elimination von Kettenregeln
Nun kümmern wir uns um die Kettenregeln. Regeln, die von einem Nonterminal auf ein Nonterminal (\(S\rightarrow A\rightarrow a\)) zeigen sind ebenfalls unnötig. Wir gehen vor wie in Schritt eins.
\(S\rightarrow AB\)
\(S\rightarrow aA\)
\(S\rightarrow a\)
\(S\rightarrow ABA\)
\(S\rightarrow AA\)
\(A\rightarrow aA\)
\(A\rightarrow a\)
\(B\rightarrow Bb\)
\(B\rightarrow b\)
3. Separation von Terminalzeichen
Jetzt sind die Terminalzeichen dran. Wir brauchen auf der rechten Seite nur Zweier-Kombinationen aus Nonterminalen oder ein einzelnes Terminal. Wir ersetzen also z.B. \(aA\) durch \(\Pi_a A\), wobei \(\Pi_a\) ein neues Nonterminal ist, welches mit einer neuen Regel auf \(a\) zeigt. Aus \(S\rightarrow aA\) wird also \(S\rightarrow\Pi_a A\) und \(\Pi_a\rightarrow a\).
\(S\rightarrow AB\)
\(S\rightarrow \Pi_aA\)
\(S\rightarrow a\)
\(S\rightarrow ABA\)
\(S\rightarrow AA\)
\(A\rightarrow \Pi_aA\)
\(A\rightarrow a\)
\(B\rightarrow B\Pi_b\)
\(B\rightarrow b\)
\(\Pi_b\rightarrow b\)
\(\Pi_a\rightarrow a\)
4. Elimination der Nonterminalketten
Letzter Schritt: zu lange Nonterminalketten auf die Maximallänge von \(2\) verkleinern. Das Vorgehen kennt ihr ja schon, es wird einfach eine neue Zwischenregel eingefügt. Aus \(S\rightarrow ABA\) werden also \(S\rightarrow S_{2}A\) und \(S_2\rightarrow AB\):
\(S\rightarrow AB\)
\(S\rightarrow \Pi_aA\)
\(S\rightarrow a\)
\(S\rightarrow S_{2}A\)
\(S_2\rightarrow AB\)
\(S\rightarrow AA\)
\(A\rightarrow \Pi_aA\)
\(A\rightarrow a\)
\(B\rightarrow B\Pi_b\)
\(B\rightarrow b\)
\(\Pi_b\rightarrow b\)
\(\Pi_a\rightarrow a\)
Fertig! Aus eindeutigen Grammatiken lassen sich auch eindeutige Chomsky-Grammatiken erstellen.
Vorteile? Jedes Wort \(\omega\) mit \(\mid\omega\mid=n\) braucht \(2n-1\) Ableitungsschritte, da jeder Ableitungsbaum (bis auf die letzte Ebene) für die Chomsky-Normalform ein Binärbaum ist und wg. \(n\) Blättern genau \(n-1\) innere Knoten hat!
(Weiterhin im Skript wurde die Greifach-Normalform angesprochen. Ebenso eine reduzierte Grammatik. Die reiche ich später nach, da sie nicht Teil der Lernziele sind.)
Antwort zum Lernziel: Eine Grammatik ist in Chomsky Normalform wenn alle Regeln/Produktionen die Form \((A\rightarrow a)\) oder \((A\rightarrow BC)\) besitzen mit \(A,B,C\in\Pi\) und \(a\in\Sigma\) ist. Aus einer beliebigen kontextfreien Grammatik lässt sich eine Chomsky Normalform-Grammatik erstellen indem man die \(\epsilon\)– und Kettenregeln eliminiert, die Terminalzeichen separiert und die Nonterminalketten mit mehr als drei Nonterminalen mittels Zwischenregeln auf maximal zwei Nonterminale verkürzt.
Lernziel 2
Was besagt das Pumping-Lemma für kontextfreie Sprachen und wie wendet man es an?
Wie in dem letzten Beitrag zu KE6 angedroht, gibt es auch ein Pumping-Lemma für kontextfreie Sprachen. Wir erinnern uns: mit dem Pumping-Lemma können wir ein Teilwort \(v\), der Zerlegung \(uvw\) eines Wortes \(\omega\) durch einen Zyklus im endlichen Automaten beliebig aufpumpen. Jedes Wort einer (unendlichen) regulären Sprache verfügt ab einer bestimmten Wortlänge über diese Eigenschaft. Bei endlichen Wortlängen können wir es uns einfacher machen, indem wir für jedes Wort einen akzeptierenden Zustand definieren und Zack! ist die Sprache regulär. Das ist der Grund warum alle endlichen Sprachen regulär sind.
Kümmern wir uns nun um das Pumping-Lemma für kontextfreie Sprachen (nicht vergessen: auch reguläre Sprachen sind kontextfrei, aber nicht alle kontextfreien Sprachen sind regulär – reguläre Sprachen sind eine echte Teilmenge der kontextfreien Sprachen). Ich schreibe die Definition (wieder aus dem Buch von Dirk W. Hoffmann) einfach mal hin und dann schauen wir sie uns genauer an:
Für jede kontextfreie Sprache \(L\) existiert ein \(j\in\mathbb{N}\), so dass sich alle Wörter \(\omega\in L\) mit \(\mid\omega\mid\geq j\) in der folgenden Form darstellen lassen:
\(\omega=uvwxy\) mit \(\mid vx\mid\geq 1\) und \(\mid vwx\mid\leq j\).
Mit \(\omega\) ist auch \(uv^{j}wx^{j}y\) für alle \(j\in\mathbb{N}_0\) in \(L\) enthalten.
Alle Wörter ab einer gewissen Länge \(j\) (unsere Pumping Zahl) enthalten Teilwörter \(v\) und \(x\), die sich aufpumpen lassen und eines davon ist nicht leer (\(\mid vx\mid\geq 1\)). Seht Ihr den Unterschied zum Pumping Lemma für reguläre Sprachen? Dort haben wir gefordert, dass wir in der Zerlegung \(uvw\) nur \(v\) beliebig aufpumpen können. Hier müssen es \(v\) und \(x\) sein. Das liegt an der evtl. fehlenden rechtslinearen Struktur der Ableitungsbäume, die nur reguläre Sprachen inne haben. Im Beispiel weiter unten wird das gleich deutlicher.
Achtung: um zu zeigen, dass eine Sprache kontextfrei ist, müssen wir nur eine kontextfreie Grammatik die sie erzeugt oder einen Kellerautomaten (kommt im nächsten Beitrag) angeben, der sie erkennt. Das Pumping Lemma ist aber dazu gedacht eine Sprache als nicht kontextfrei zu erkennen (was leider auch nicht immer klappt, dazu gleich mehr).
Erklärung
Wir haben schon massive Vorarbeit geleistet und den Ableitungsbaum einer kontextfreien Sprache in Chomsky-Normalform als binären Baum entlarvt. Seine Eigenschaften erlauben es uns einige Eigenschaften für ein Wort abzuleiten, dass wir für das Pumping Lemma brauchen. Nehmen wir zunächst eine Grammatik \(G=(\Pi,\Sigma,R,S)\) in Chomsky Normalform. Durch diese Normalform hat der Baum im Inneren die Form eines Binärbaums mit \(2 ^{\mid\Pi\mid}\) Blättern. Wir können also einen Pfad wählen, der min. die Länge \(\mid\Pi\mid\) aufweist. Mit dem Startsymbol zusammen haben wir auf dem Pfad min. \(\mid\Pi\mid +1\) Nonterminale, so dass eines davon mehrfach aufgetaucht sein muss (erinnert Ihr euch? Unser Zyklus im Automaten!).
Zur Erinnerung: Das \(j\) ist unsere Pumping Zahl. Jeder Ableitungsschritt ist ein durchlaufener Zustand in der Maschine, so dass wir bei einer unendlichen Länge an Worten irgendwann durch einen Zyklus bei der Erzeugung eines Wortes laufen müssen. Im Ableitungsbaum haben wir somit tatsächlich mehrmals ein Nonterminal stehen. Nennen wir das Nonterminal einfach mal \(A\) und unterteilen das Wort in \(uvwxy\).
Um also aus dem Nonterminal \(A\) noch einmal ein \(A\) herzustellen, muss min. ein Ableitungsschritt \(A\rightarrow BC\) durchlaufen werden. D.h. eines der Segmente \(v\) oder \(x\) hat min. ein Terminal drin. Das folgt aufgrund der Regelstruktur in der Chomsky Normalform.
Wie \(u\) oder \(w\) aussehen, haben wir keine Ahnung. Macht aber nichts, denn aufgrund dem Doppelvorkommen von \(A\) können wir die Teilworte \(v\) und \(x\) aufpumpen und beliebige Worte der Form \(uv^{i}wx^{i}y\) erzeugen indem wir die Ableitungssequenz, ausgehend von unserem Nonterminal \(A\) mehrfach für das Mittelstück wiederholen.
Dabei wird jedoch nicht nur ein Teil (wie beim Pumping-Lemma für reguläre Sprachen) wiederholt, sondern zwei.
Ein Beispiel wäre wohl sinnig, oder?
Beispiel: \(L_1=\{\{ab\}^n\mid n\in\mathbb{N}\}\Rightarrow(abababab…)\)
Die Sprache besteht aus einer unendlichen Kombination aus \(ab\) und ist sogar regulär, d.h. wir hätten darauf auch das Pumping-Lemma für reguläre Sprachen anwenden können. Da reguläre Sprachen aber auch kontextfrei sind (und ich zu faul bin mir was neues auszudenken), klappt das Pumping Lemma für kontextfreie Sprachen hier auch.
Wir suchen also eine Zerlegung \(uvwxy\), so dass gilt \(uv^{i}wx^{i}y\in L_1\), mit \(i\in\mathbb{N}_0\) wobei \(u\) und \(y\) ruhig leer sein dürfen. Außerdem muss gelten \(\mid vx\mid\geq 1\) und \(\mid vwx\mid\leq j\).
Dazu brauchen wir unsere Pumping Zahl \(j\), die als Mindestlänge für das Wort fungiert. Wollen wir einfach mal \(j=10\) nehmen. Unser Wort der Länge \(10\) sieht also wie folgt aus: \(ababababab\). Wir zerlegen das willkürlich (jede andere Zerlegung, die die Voraussetzungen erfüllt ist möglich) in \(u=ab,v=ab,w=ab,x=ab,y=ab\) und prüfen ob die oben genannten Voraussetzungen gelten:
\(\mid abab\mid = 4\geq 1\) (passt) und
\(\mid ababab\mid = 6\leq 10\) (passt auch)
Muss auch nur noch (ich klammere für Übersichtlichkeit aus)
\(\{ab\} \{ab\}^{i}\{ab\}\{ ab\}^{i}\{ab\}\in L_1\) mit \(i\in\mathbb{N}_0\)
gelten. Aber das prüfen wir zuletzt.
Eine Regelmenge in Chomsky Normalform, die diese Sprache erzeugt wäre z.B. die folgende:
\(S\rightarrow\Pi_a B\)
\(B\rightarrow\Pi_b C\)
\(B\rightarrow C\)
\(C\rightarrow\Pi_a B\)
\(\Pi_a\rightarrow a\)
\(\Pi_b\rightarrow b\)
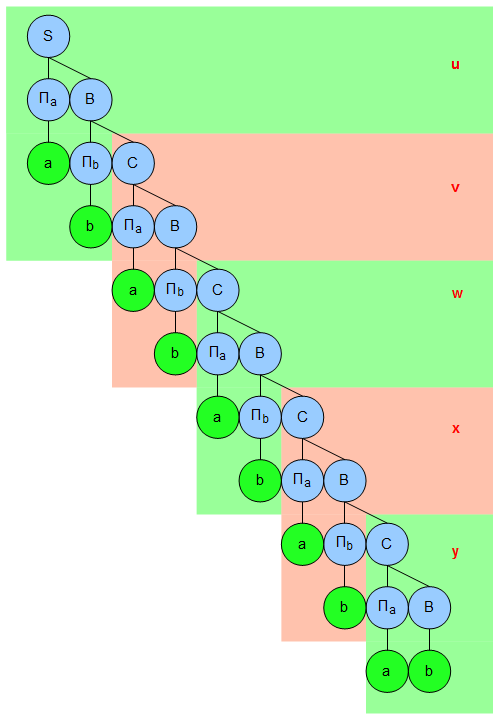
Es ist zwar nicht notwendig sie anzugeben, aber ich würde euch gerne den Ableitungsbaum für das zu zerlegende Wort \(ababababab\) zeigen. Das verdeutlicht das Lemma etwas besser.
Mal nebenbei: aus diesem Grund werden reguläre Grammatiken auch rechtslineare Grammatiken genannt: der Baum kippt, wie Ihr sehen könnt, nach rechts weg. Das ist der Grund, warum wir im Pumping Lemma für reguläre Sprachen nicht zwei, sondern nur ein Teilwort aufpumpen müssen.
Es ist leicht einzusehen, dass wir hier bereits ab \(u\) einen Zyklus haben, der sich bis \(y\) durchzieht. \(u\) und \(y\) könnten aber auch leer sein, wäre für unser Lemma egal. Wichtig ist, dass wir \(v\) und \(x\) wie im Lemma gefordert aufpumpen können und das Wort immer noch in \(L_1\) liegt.
Und was würde passieren wenn wir \(v\) oder \(x\) entfernen (\(i=0\)) oder beliebig aufpumpen (\(i\geq0\)) um die letzte Voraussetzung \(ab ab^{i}ab ab^{i} ab\in L_1\) mit \(i\in\mathbb{N}_0\) zu erfüllen? Probieren wir das mal aus (ich klammere \(uvwxy\) der Übersichtlichkeit halber aus):
\(i=0\Rightarrow\{ab\}\{\}\{ab\}\{\}\{ab\}\)
\(i=1\Rightarrow\{ab\}\{ab\}\{ab\}\{ab\}\{ab\}\)
\(i=2\Rightarrow\{ab\}\{abab\}\{ab\}\{abab\}\{ab\}\)
\(…\)
Und? Sind die Worte in \(L_1\)? Ja, sie sind es. Damit ist die Sprache kontextfrei.
Wichtig: meine der Faulheit geschuldete Wahl einer regulären Sprache als Beispiel ist aufgrund der rechtslinearen Struktur des Baumes vielleicht nicht optimal gewesen, denn genau das macht – wie eiter oben erwähnt – den Unterschied zwischen den beidem Lemmata aus.
Während bei einer regulären Sprache der Ableitungsbaum nach rechts kippt und wir nur das \(v\), d.h. den rechten Teilbaum in der Zerlegung \(uvw\) betrachten müssten, so könnte bei einer kontextfreien (aber nicht regulären und damit auch nicht rechtslinearen) Sprache der Ableitungsbaum gleichzeitig nach links und rechts aufspannen. Das ist der Grund, warum wir den Baum nicht in drei, sondern in fünf Teile zerlegen (nämlich \(uvwxy\)) und beide Äste, links und rechts, mit \(v\) und \(x\) betrachten müssen.
Denn bei den regulären Sprachen wird mit \(v\) nur der rechte Teilbaum aufgepumpt (wir haben ja aufgrund der rechtslinearen Struktur der regulären Sprachen keinen anderen), während es bei den kontextfreien (aber nicht unbedingt regulären) Sprachen möglich sein muss beide Teilbäume \(v\) und \(x\) verlängern zu können. Soweit klar? Evtl. reiche ich ein anderes Beispiel nach um es zu verdeutlichen.
Lust auf ein Negativbeispiel?
Beispiel: \(L_2=\{a^n b^n c^n\mid n\in\mathbb{N}\}\Rightarrow(abc,aabbcc,…)\)
Auch hier suchen wir einer Zerlegung \(uvwxy\) mit den oben genannten Eigenschaften:
\(\mid vx\mid\geq 1\),
\(\mid vwx\mid\leq j\) und
\(uv^{i}wx^{i}y\in L_2\), mit \(i\in\mathbb{N}_0\)
Wir brauchen wieder unsere Pumping Zahl \(j\), aber zunächst schauen wir uns die Worte doch einmal an für \(n\leq3\):
\(n=1\Rightarrow abc\)
\(n=2\Rightarrow aabbcc\)
\(n=3\Rightarrow aaabbbccc\)
Fällt euch schon etwas auf? Versucht doch einmal eine Zerlegung \(vwx\) (denn \(u\) und \(y\) dürfen ja ruhig leer sein) z.B. von \(aaabbbccc\) mit den oben genannten Kriterien anzugeben. Ich mache einfach mal ein paar Beispielzerlegungen für das Wort der Länge \(6\), d.h. \(j=6\):
Während Ihr die ersten beiden Kriterien \(\mid vx\mid\geq 1\) und \(\mid vwx\mid\leq 6\) noch erfüllen könnt, sieht es mit \(uv^{i}wx^{i}y\in L_2\), mit \(i\in\mathbb{N}_0\) schon sehr düster aus. Versuchen (\(u\) und \(y\) bleiben einfach mal leer, die sind uns egal. Ich klammere \(vwx\) wieder für die Übersichtlichkeit aus)?
Zerlegung Nr. 1:
\(i=0\Rightarrow\{u\}\{\}\{bbb\}\{\}\{y\}\notin L_2\)
Bereits mit \(i=0\) klappt es nicht. Das erzeugte* Wort ist nicht in unserer untersuchten Sprache. (*was ist das Gegenteil von aufgepumpt? Abgepumpt?)
\(i=1\Rightarrow\{u\}\{aaa\}\{bbb\}\{ccc\}\{y\}\in L_2\)
Hier geht es noch. Ist aber auch kein Wunder, denn das ist ja unser von Anfang an ausgesuchtes Wort, dass wir zerlegen wollten.
\(i=2\Rightarrow\{u\}\{aaaaaa\}\{bbb\}\{cccccc\}\{y\}\notin L_2\)
Und ab hier geht es dann nicht mehr weiter. Seht Ihr warum? Wir müssen bei der Erhöhung von \(i\) zwei Teile des Wortes verlängern: \(v\) und \(x\). Dabei bleibt aber ein Teil auf der Strecke, der nicht mit verlängert wird: \(w\). Das sind unsere \(b’s\). Das ist aber Voraussetzung, denn in der Sprache sind nur Worte, die die gleiche Anzahl \(a’s\) wie \(b’s\) und \(c’s\) haben.
Zerlegung Nr. 2:
\(i=0\Rightarrow\{u\}\{\}\{abbb\}\{\}\{y\}\notin L_2\)
Auch hier: nix.
\(i=1\Rightarrow\{u\}\{aa\}\{abbb\}\{ccc\}\{y\}\in L_2\)
Wie gerade eben: unser ausgesuchtes Wort, was natürlich funktioniert.
\(i=2\Rightarrow\{u\}\{aaaa\}\{abbb\}\{cccccc\}\{y\}\notin L_2\)
Wieder eine unterschiedliche Anzahl an \(a’s\), \(b’s\) und \(c’s\). War also wieder nichts.
Zerlegung Nr. 3:
\(i=0\Rightarrow\{u\}\{\}\{bbbc\}\{\}\{y\}\notin L_2\)
Nope.
\(i=1\Rightarrow\{u\}\{aaa\}\{bbbc\}\{cc\}\{y\}\in L_2\)
Erneut: unser ausgesuchtes Wort, was wieder funktioniert.
\(i=2\Rightarrow\{u\}\{aaaaaa\}\{bbbc\}\{cccc\}\{y\}\notin L_2\)
Auch hier: Wieder eine unterschiedliche Anzahl an \(a’s\), \(b’s\) und \(c’s\). Keine Chance.
Ich will euch nicht weiter quälen: Ihr seht, dass es einfach nicht funktioniert, egal welche Pumping Zahl \(j\) und welche Zerlegung wir wählen. Während wir zwei Teilworte \(v\) und \(x\) für das Lemma verlängern müssen, bleibt eine immer auf der Strecke. D.h. die Zusammensetzung der Elemente ist abhängig von Ihrer Umgebung, ihrem Kontext! Damit ist die Sprache \(L_2\) nicht kontextfrei, sondern kontextsensitiv.
Etwas will ich euch aber nicht vorenthalten: denn das Pumping Lemma funktioniert nicht immer. Es gibt kontextsensitive Sprachen, die das Lemma dennoch erfüllen! Das Problem liegt in der Startposition der Teilwörter der Zerlegung. Denn dazu macht das Lemma keine Aussage (Prefix \(u\) und Suffix \(y\) können ja leer sein). Gelingt es uns den kritischen Abschnitt im Wort (in unserem Beispiel war das \(w\)) irgendwie zu umgehen, so haben wir eine evtl. kontextsensitive Sprache, die unser Pumping Lemma trotzdem erfüllt. Ein Beispiel hierzu ist die Sprache:
\(L_3=\{b^k c^l d^m\mid k,l,m\in\mathbb{N}\}\cup\{a^m b^n c^n d^n\mid m,n\in\mathbb{N}\}\)
Hier versagt das Pumping Lemma für kontextfreie Sprachen, den \(L_3\) erfüllt bei einer geschickten Wahl von \(j\) und einer Zerlegung \(uvwxy\) alle drei Lemma-Kriterien. Ich möchte hier nicht näher darauf eingehen, da das im Skript nicht behandelt wurde (tue es bei Gelegenheit aber trotzdem wenn etwas Zeit ist). Aber mit Ogdens Lemma kann man diese kontextsensitive Sprache auch als eine solche erkennen!
Antwort zum Lernziel: Das Pumping Lemma für kontextfreie Sprachen besagt, dass es bei einem Wort mit Mindestlänge \(j\) eine Zerlegung \(uvwxy\) geben muss, die folgende Kriterien erfüllt:
\(\mid vx\mid\geq 1\),
\(\mid vwx\mid\leq j\) und
\(uv^{i}wx^{i}y\in L_2\), mit \(i\in\mathbb{N}_0\)
Dabei werden die Teilworte \(v\) und \(x\) beliebig aufgepumpt. Sollte keine Zerlegung diese Kriterien erfüllen, so ist die Sprache auch nicht kontextfrei.
Angewandt wird es, indem man sich zunächst ein Wort aus der zu untersuchenden Sprache sucht und eine Zerlegung angibt, welche die oben genannten Kriterien für alle \(i\in\mathbb{N}_0\) erfüllt. Liegt das neue Wort mit den aufgepumpten Teilworten \(v\) und \(x\) dann nicht in der Sprache, zu der das Ursprungswort gehörte, so ist die Sprache auch nicht kontextfrei.
Es gibt jedoch Sprachen, die nicht kontextfrei sind und das Lemma dennoch erfüllen. Mit Ogdens Lemma kann man diese jedoch als nicht kontextfrei nachweisen.
Das war Teil 1 von 3 der Kurseinheit 7.
Bei Fehlern wieder die große Bitte: ab damit in die Kommentare damit ich das schleunigst berichtigen kann. Vor allem in mathematischen Kursen sind Fehler eine ungemein frustrierende Lernbehinderung, wie ich in Computersysteme 1 und 2 erfahren durfte: da zweifelt man schon tagelang an seinem Rechenweg weil im Skript ein anderes Ergebnis rauskommt. Das ist nervig!