TIB: Endliche Automaten und kontextfreie Grammatiken (Lernziele KE6 3/3)

Lernziel 7

Was sind Ableitungsbäume kontextfreier Grammatiken?

Wie wir aus dem Beitrag zu KE5 bereits wissen, sind reguläre Sprachen (Typ-3, rechte Seite einer Regel besteht nur aus einem Terminal, dem ein Nonterminal folgt oder einem leeren Wort) eine echte Teilmenge der kontextfreien Sprachen (Typ-2, linke Seite der Regel besteht nur aus einem Nonterminal). Die Typ-3-Sprachen sind nur noch ein Stück weiter eingeschränkt . Damit sind reguläre Sprachen auch kontextfrei, denn alle Nonterminale können unabhängig von ihrer Umgebung ersetzt werden (im Gegensatz zu Typ-1-Grammatiken, die auch kontextsensitive Regeln erlauben, dort kann die linke Seite der Regel auch aus einem Terminal und einem Nonterminal bestehen. Der Kontext ist also die Verbindung von Terminal und Nonterminal im Wort).

Wenn man nach Ableitungsbäumen und kontextfreien Grammatiken sucht, findet man diesen Beitrag in der Wikipedia und der Fall ist eig. klar. Leider hat das Skript auch noch 4 Seiten zum Thema der Notation für die kontextfreie Grammatik (die polnische Notation und die vereinfachte Notation). Anschließend geht es um die abstrakte Syntax, das Erzeugungssystem, die abstrakte Semantik und dann drei Arten von Ableitungsbäumen. Nun stellt sich mir die Frage, ob ich einfach ein paar Beispiele für den Ableitungsbaum aus dem Artikel bringen oder das Skript sezieren soll. Just in diesem Moment entscheide ich mich für Ersteres in Kombination mit dem Beispiel aus dem Skript.

Zunächst haben wir drei Arten von Ableitungsbäumen:

1. Baum mit Wurzel $a$ und Front $a\in(\Sigma\cup\Pi)$. Das ist ein ein einzelner Knoten $a$, der gleichzeitig auch die Wurzel ist. $a$ kann nur ein Wort über der Menge der Terminale und Nonterminale sein. Die Wurzel ist das ausgehende Zeichen, d.h. das Startsymbol (in diesem Fall ist es nicht die Startregel aus $R$).
2. Baum mit Wurzel $A$ (Nonterminal) und Front $\epsilon$ (leeres Wort) wenn es die folgende Abschlussregel in der Grammatik gibt: $(R\rightarrow\epsilon)$.
3. Und hier endlich der "echte" Baum mit einer Wurzel $A$ und einer Front $\omega$ wenn es eine Ableitungssequenz gibt, so dass man das Wort $\omega$ mittels der Regeln aus der Grammatik ableiten kann.

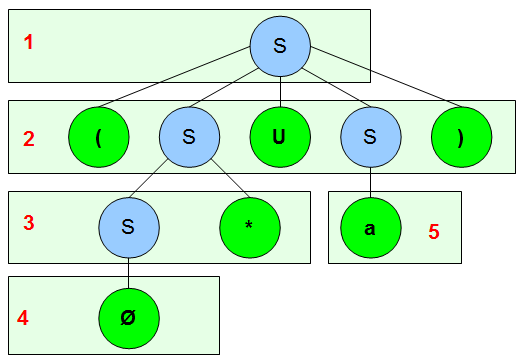
Bitte macht euch noch einmal klar, dass die Front das abgeleitete Wort (oder Zeichen) ist und die Wurzel das Startsymbol (was nicht unbedingt die Startregel sein muss). Die folgende Abbildung zeigt zwei Bäume (mit grüner Front), die auch im Skript Verwendung finden mittels der Regelmenge:

$S\rightarrow a\mid b\mid\emptyset\mid (S\cup S)\mid (SS)\mid S^{*}$

Beispiel: Ableitung von $\emptyset$ (mittels Baumart Nr. 1)

Sequenz: nicht notwendig, da nur Baumart Nr. 1

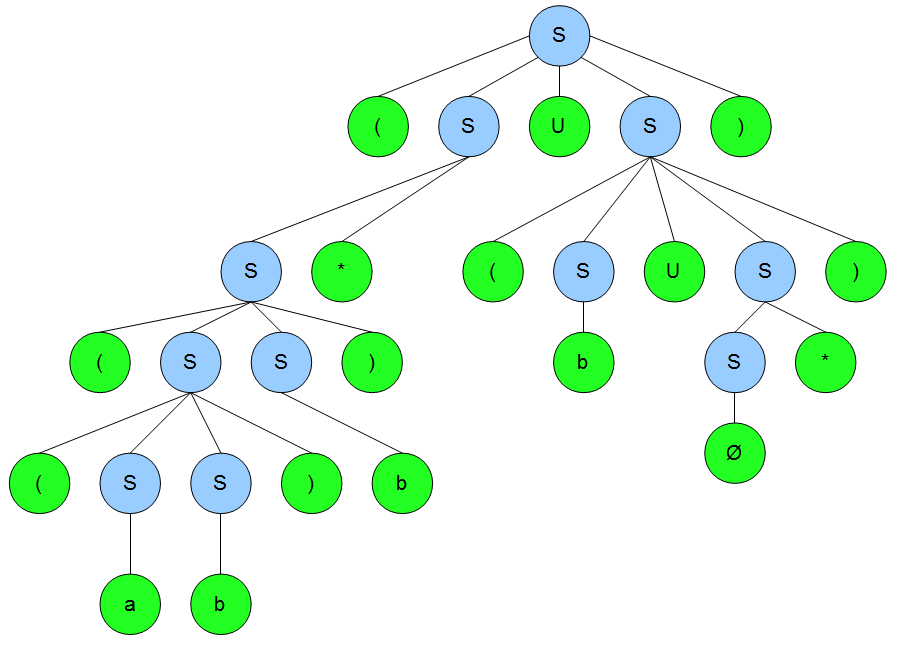
Beispiel: Ableitung von $(\emptyset^{*}\cup a)$ (mittels Baumart Nr. 3)

Sequenz: $S\Rightarrow(S\cup S)\Rightarrow(S^{*}\cup S)\Rightarrow(\emptyset^{*}\cup S)\Rightarrow(\emptyset^{*}\cup a)$

Den Baum baut man so sukzessive auf. In der Abbildung sind die einzelnen Ableitungsschritte der Sequenz von $1-5$ nummeriert. Am Ende liest man einfach nur das gesuchte Wort $\omega$ anhand der Blätter (Knoten ohne Kinder) von links nach rechts ab (auch Tiefensuche genannt).

Baumart Nr. 2 kam für ein Beispiel nicht in Frage, da wir das leere Wort $\epsilon$ mangels passender Regel nicht ableiten können (siehe unsere Regelmenge) und ich zu faul war eine neue Regelmenge zu definieren. Evtl. hole ich das noch nach wenn die Zusammenfassungen zu allen Kurseinheiten online sind.

Noch eine Kleinigkeit zur Notation:

Wenn das Wort $\omega$ einen Ableitungsbaum mit Wurzel $A$ und Front $\omega$ hat, so gilt $A\xrightarrow{\text{*}}\omega$

Es könnte auch mehrere Ableitungsbäume für ein Wort geben. Nehmen wir wieder das Beispiel aus dem Skript:

Beispiel: $S\rightarrow SS\mid a\mid b$ und abgeleitetes Wort $aba$

Sequenz 1: $S\Rightarrow SS\Rightarrow SSS\Rightarrow aSS\Rightarrow abS\Rightarrow aba$

Sequenz 2: $S\Rightarrow SS\Rightarrow aS\Rightarrow aSS\Rightarrow abS\Rightarrow aba$

Durch die unterschiedlichen Ableitungssequenzen für ein Wort, haben wir auch unterschiedliche Ableitungsbäume. Damit ist die Grammatik aus diesem Beispiel mehrdeutig.

Antwort zum Lernziel: der Ableitungsbaum bezeichnet die baumförmige Darstellung der Ableitung eines Wort $\omega$ aus einer Grammatik. Sobald der Baum aufgebaut ist, wird das Wort von links nach rechts anhand der Blätter abgelesen (Tiefensuche).

Lernziel 8

Wann ist eine kontextfreie Grammatik bzw. Sprache eindeutig?

Wie wir im letzten Beispiel gesehen haben, kann es zu einen Wort mehrere Ableitungsbäume geben. Diese Grammatiken sind für die Syntaxdefinition von Programmiersprachen aufgrund dieser Mehrdeutigkeit jedoch unbrauchbar. Der Programmtext würde sich so auf verschiedene Weise ableiten lassen. Wir sind also auf eindeutige Grammatiken für Programiersprachen angewiesen.

Eine eindeutige Grammatik ist also dann eindeutig wenn jedes Wort aus der durch die Grammatik definierten Sprache genau einen Ableitungsbaum hat. Ebenso verhält es sich mit der Sprache: sie ist dann eindeutig wenn es eine eindeutige Grammatik gibt, dass die Sprache beschreibt.

Man kann die Mehrdeutigkeit auch durch die Verwendung von Präzedenzregeln eliminieren. Da das nicht Teil des Skripts war, lasse ich das zunächst einmal aus. Wenn mehr Zeit ist, schreibe ich evtl. noch ein paar Zeilen dazu. Bis dahin sei auf ein PDF der Uni Marburg zum Thema verwiesen.

Antwort zum Lernziel: siehe Definition von oben.

Ausgelassen habe ich hier die abstrakten Syntaxbäume, da sie nicht in den Lernzielen erwähnt werden. Aber vielleicht der Vollständigkeit halber noch ein paar Worte zum Thema: Was ist also diese abstrakte Syntax?

Sie ist nichts anderes als die wesentlichen Teile des Ableitungsbaumes zu einem Ausdruck. Genau dieser Syntaxbaum wird auch vom Compiler verwendet um den Programmcode zu interpretieren, da der Ableitungsbaum (auch "konkreter Syntaxbaum" statt Ableitungsbaum genannt) zu viele Informationen beinhaltet, die unwichtig sind. Die Informationen können auch in in anderer Form gespeichert werden.

Dazu bemühe ich wieder das Beispiel aus dem Skript mit der Regelmenge

$S\rightarrow a\mid b\mid\emptyset\mid (S\cup S)\mid (SS)\mid S^{*}$

aus der verwendeten (eindeutigen) Grammatik.

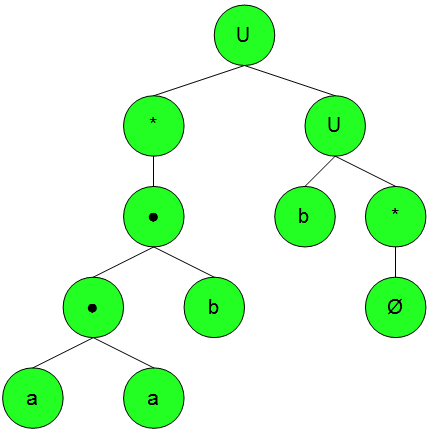
Beispiel: abgeleiteter Ausdruck $(((aa)b)^{*}\cup(b\cup\emptyset^{*}))$

Sequenz: $S\Rightarrow(S\cup S)\Rightarrow(S^{*}\cup (S\cup S))\Rightarrow((SS)^{*}\cup (b\cup S^{*}))\Rightarrow((SS)b^{*}\cup (b\cup\emptyset^{*}))\Rightarrow((aa)b^{*}\cup (b\cup\emptyset^{*}))$

Die folgende Abbildung zeigt den zugehörigen Ableitungsbaum (konkreter Syntaxbaum):

Für uns spannend sind aber nicht die konkreten Ableitungsinformationen, sondern einfach nur die abstrakte Syntax. Entfernen wir nun alle unnötigen Knoten aus dem Ableitungsbaum (konkreter Syntaxbaum), so bekommen wir unseren sehr kompakten abstrakten Syntaxbaum.

Wie man sich leicht vorstellen kann, kann dieser Baum deutlich einfacher gespeichert und geparsed werden als sein großer Bruder.

Eine schöne Darstellung findet sich auch in einigen Folien aus Magdeburg. Im Kurs 1810 (Compilerbau) der FernUni wird verstärkt darauf Bezug genommen. Wer sich diesen Kurs im Studium als Modul anhören möchte (ist im Katalog B), sollte sich diese Bäumchen evtl. genauer ansehen.

Damit haben wir auch KE6 hinter uns. Bei Fehler gilt wie immer: so schnell wie möglich in die Kommentare.

Datum: 2. Juni 2013
Kategorie: Theoretische Informatik
Kommentarfeed: RSS 2.0 • Trackback: Trackback-Url

Sie können zum Ende springen und ein Kommentar hinterlassen. Pingen ist im Augenblick nicht erlaubt.