Autor: Anton

Bei dem \(P-NP\)-Problem geht es um die Frage wie die beiden Komplexitätsklassen zueinander stehen. Das Skript fasst sich nur sehr kurz, was  dieses Thema angeht, so dass ich beschlossen habe es hier noch einmal im Detail aufzuarbeiten.

Das \(P-NP\)-Problem gehört zu den Millenium-Problemen, d.h. es winken eine Million USD wenn es gelöst wird. Aber eine Million USD sind im Vergleich zu den Folgen, die z.B. \(P=NP\) (beide Komplexitätsklassen sind gleich) auslösen würde keine Erwähnung wert. Es wäre uns auf einen Schlag möglich für jedes Problem in \(NP\) einen effizienten Algorithmus anzugeben.

Als Beispiel nehmen wir das Faktorisierungsverfahren, auf dem sehr viele kryptographische Algorithmen (u.a. RSA oder das Verfahren von Diffie-Hellmann zum Schlüsselaustausch) basieren. Diese Algorithmen gehen davon aus, dass das Faktorisierungsproblem nicht effizient zu lösen ist. Es wäre das blanke Chaos, würde sich herausstellen, dass \(P=NP\). \(P\neq NP\) wäre hingegen nicht so schlimm.

Machen wir uns einmal klar, was \(P\) und \(NP\) denn nun wirklich sind. Dazu betrachten wir zunächst eine etwas größere Klasse.

Klassifizierung \(EXPTIME\)

In \(EXPTIME\) liegen Probleme, die auf einer deterministischen Turingmaschine in \(O(2^n)\), d.h. in exponentieller Zeit, entschieden werden können. Hier ist \(n\) die Eingabelänge.

Es ist nicht schwer zu sehen, dass man hier nur für sehr kleine Probleminstanzen effizient nach einer Lösung suchen kann. Für größere Eingabelängen \(n\) wird die Suche ungleich schwerer.

Was wäre so ein Problem, dass deterministisch in exponentieller Zeit lösbar wäre? Na klar, das Problem des Handlungsreisenden (auch TSP, travelling salesman, genannt). Der folgende Abschnitt basiert mehrheitlich auf dem Artikel aus der Wikipedia.

Beispiel TSP

Das TSP gehört zur der Klasse der Optimierungsprobleme. Bei diesem Problem geht es darum für eine gegebene Anzahl Städte und einer Entfernung zwischen diesen den kürzesten Weg für einen Rundkurs zu finden.

Diese Problem hat eine Vielzahl an Anwendungsmöglichkeiten (Logistik, Design von Mikrochips, etc.), so dass eine optimale Lösung durchaus wünschenswert erscheint.

Leider haben wir hier, in Abhängigkeit der Anzahl der zu besuchenden Punkte, nur dann eine optimale Lösung wenn wir jeden Punkt prüfen. Das Wachstum ist also exponentiell und zweifellos gehört TSP zur Klasse \(EXPTIME\), zumindest bei seinem deterministischen Lösungsansatz.

Auch wenn mittlerweile für mehrere Tausend Punkte optimale Lösungen durch heuristische und exakte Verfahren gefunden wurden, so bleibt das Problem gleich: mit wachsendem \(n\) (der Anzahl der Punkte) steigt unser Aufwand immer noch exponentiell.

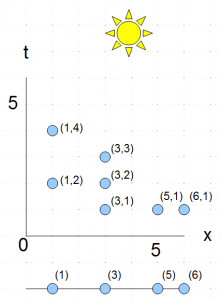
Graphisch ausgedrückt (geklaut aus der Wikipedia):

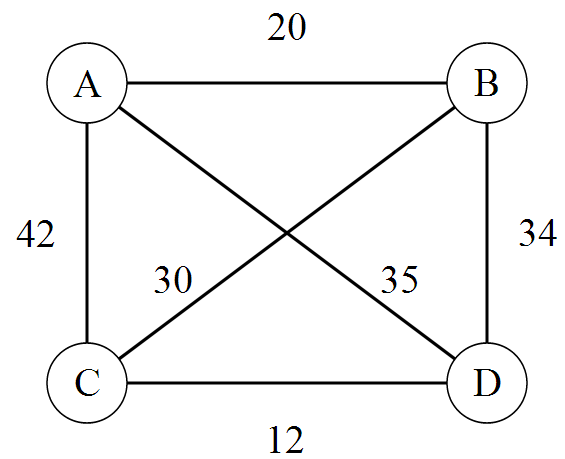
Frage: Wie ist der kürzeste Weg von \(A\) nach \(A\) über alle Punkte?

Während das bei \(4\) Punkten noch einfach ist, wird es für \(100.000\) Punkte schon deutlich schwerer.

Es sind derzeit nur effiziente, heuristische Algorithmen bekannt, die die Lösung approximieren. Z.B. der Algorithmus von Christofides, der in polynomieller Laufzeit eine Lösung approximieren kann, die maximal \(1.5\) Mal so lang ist wie die optimale Lösung.

Für exakte Lösungen gilt: jede Rundreise muss berechnet und die kürzeste ausgewählt werden. Bei \(15\) Städten haben wir \(43\) Mrd. Möglichkeiten. Hat man einen Rechner, der die Lösung für \(30\) Städte in einer Stunde berechnet, dann braucht dieser für zwei zusätzliche Städte annähernd die tausendfache Zeit; das sind mehr als \(40\) Tage.

Die Folien der RWTH Aachen zeigen eine schöne Tabelle, die ich hier Snapshotten möchte:

Das Beispiel führt vor Augen, dass uns sehr daran gelegen, dass wir Probleme nicht in Exponentialzeit lösen müssen.

Nachdem wir die Optimierungsvariante haben, kommen wir zum Bindeglied des \(TSP\) zu der Klasse \(NP\): uns geht es zunächst nicht um Optimierung, sondern um eine Entscheidung.

Die Entscheidungsvariante des \(TSP\) ist:

Gibt es eine Tour mit Kosten \({}\leq b\)?

Und hier beginnt unsere Reise: während wir hier wieder alle Wege durchprobieren und so in der Klasse der Exponentialzeit-Algorithmen landen, können wir uns das Leben deutlich einfacher machen. Aber dazu gleich mehr.

Ich gehe auf das \(TSP\) nun nicht weiter ein, da es mir nur um \(P-NP\) geht und die Ausführungen bis hierhin für diese Betrachtung ausreichen.

Kleiner Exkurs zum Schluss: Durch die Hierarchiesätze können wir z.B. zeigen, dass \(P\subsetneq EXPTIME\) ist. Damit gibt es in \(EXPTIME\) Probleme, die nicht in \(P\) liegen.

Klassifizierung \(P\)

Ein Problem in \(P\) bedeutet, dass es effizient lösbar ist. Effizient heißt: die deterministische Turingmaschine, die das Problem löst ist nach oben durch ein Polynom \(n^k\) beschränkt, wobei \(n\) die Länge der Eingabe ist. Wichtig hieran ist: \(k\) ist zwar beliebig, aber absolut unabhängig von unserer Eingabe!

Ein Beispiel für ein Problem in der Komplexitätsklasse \(P\) ist das \(PRIMES\).

Beispiel \(PRIMES\)

Hier ist die Frage ob eine Zahl \(x\) eine Primzahl ist oder nicht.

Die Antwort auf diese Frage ist ziemlich simpel: wir testen einfach aus ob alle Zahlen von \(2\) bis \(x-1\) unsere Zahl \(x\) ohne Rest teilen können. Wenn das nicht der Fall ist, ist die Zahl eine Primzahl.

Mit dem AKS-Algorithmus gibt es sogar einen, der das in Polynomzeit entscheiden kann. Damit gehört \(PRIMES\) tatsächlich zur Komplexitätsklasse \(P\).

Nach dem der Urvater der AKS-Algorithmen gefunden wurde, wurden weitere ersonnen, die die Laufzeit noch ein Stück nach unten korrigierten. Der schnellste bekannte Algorithmus aus der AKS-Familie terminiert in \(O((log\text{ }N)^{6+\varepsilon})\).

Kommen wir nun zur Komplexitätsklasse, die uns so brennend interessiert.

Klassifizierung \(NP\)

Ist ein Problem in \(NP\), so bedeutet es, dass es effizient prüfbar ist. In diesem Fall heißt effizient ebenfalls: die deterministische Turingmaschine, die prüft ob das Zertifikat \(z\) zum Problem \(X\) (ein Zertifikat ist ein Lösungsvorschlag für ein Problem), ist nach oben durch ein Polynom \(n^k\) beschränkt, wobei \(n\) die Länge der Eingabe ist.

Gemerkt, was der Unterschied zwischen \(NP\) und \(P\) ist? Es ist ein Unterschied ob wir ein Problem lösen oder „nur“ einen Lösungsvorschlag prüfen.

Was bedeutet es für unser \(TSP\)?

Beispiel \(TSP\)-Instanz

Nehmen wir unsere \(4\) Punkte aus dem obigen Beispiel und stellen uns die Frage:

Gibt es einen Weg von \(A\) nach \(A\) mit Länge \({}\leq{100}\)?

Das ist ein Entscheidungsproblem. Und hier müssten wir im schlimmsten Fall nun alle Wege durchprobieren bis wir einen Weg finden, der kürzer als/gleich \(100\) ist. Was bei vielen Punkten schon eine beträchtliche Zeit in Anspruch nehmen kann, wie wir gesehen haben. Dieses „Durchprobieren“ ist genau unser \(N\) aus \(NP\). Das Orakeln einer Lösung.

Lassen wir das Orakeln weg und geben eine Lösung vor, bleibt nur noch \(P\): die Prüfung einer gegebenen Lösung auf ihre Korrektheit. Und das können wir ziemlich zackig bewerkstelligen:

Wir prüfen die Kanten zwischen den Knoten und rechnen sie einfach zusammen:

\(A\rightarrow{C}\rightarrow{D}\rightarrow{B}\rightarrow{A}\Rightarrow{{42}\rightarrow{12}\rightarrow{34}\rightarrow{20}=108}\)

Nope, das war nichts. Versuchen wir es mit:

\(A\rightarrow{D}\rightarrow{C}\rightarrow{B}\rightarrow{A}\Rightarrow{{35}\rightarrow{12}\rightarrow{30}\rightarrow{20}=97}\)

Bingo!

Man sieht leicht, dass wir zur Prüfung einer vorgegebenen Lösung auf einer deterministischen Turingmaschine deutlich weniger Zeit benötigen als alle Wege durchzuprobieren.

Und nun holen wir uns unser \(N\) aus \(NP\), indem wir orakeln. Wir raten einfach alle Kombinationen und prüfen sie polynomiell durch unsere deterministische „Kontrollturingmaschine“.

Im Schlimmsten Fall haben wir zwar immer noch einen exponentiellen Aufwand, aber vielleicht raten wir so gut, dass die Kombination \(A\rightarrow{D}\rightarrow{C}\rightarrow{B}\rightarrow{A}\) die erste geratene Möglichkeit ist und wir schon nach dem ersten Orakeln eine Lösung gefunden haben.

Und genau das bedeutet \(NP\): raten und prüfen. Oder ganz, ganz frei interpretiert: Orakel\(N\) und \(P\)rüfen.

Codieren wir den Graphen als Turingmaschine, so hat z.B. der Zustand \(A\) drei mögliche Folgezustände (wir können zu \(B\), \(C\) oder \(D\) reisen). Es existieren also drei mögliche Zustandsübergänge, von denen wir einen wählen können. Genau hier beginnt das Raten/Orakeln, unser \(N\) aus \(NP\). Anschließend haben wir zwei Möglichkeiten zur Auswahl, usw.

So geht dann unsere \(NTM\) für das \(TSP\) vor und rät eine Rundreise. Wir brechen ab wenn die Kosten höher sind als \(b\) oder wir bei unserem Ausgangsknoten landen ohne alle Knoten besucht zu haben.

Zusammenfassend lässt sich sagen: \(NP\) bedeutet orakeln und prüfen. Und das Prüfen geschieht in maximal polynomieller Zeit.

Habt Ihr nun ein Gefühl dafür, was \(NP\) bedeutet? Gut.

Nachdem wir nun alle notwendigen Komplexitätsklassen \(EXPTIME\), \(P\) und \(NP\) besprochen haben, sollte euch klar sein wie der Zusammenhang zwischen \(P\) und \(NP\) ist.

Jetzt können wir auch die Frage stellen, die das \(P-NP\)-Problem beschreibt:

Gilt \(P=NP\) oder \(P\neq{NP}\)?

In Worten:

Sind die Klassen \(P\) und \(NP\) gleich oder nicht,

bzw.

kann jede Sprache, die nicht-deterministisch in Polynomzeit entschieden werden kann auch deterministisch in Polynomzeit entschieden werden?

Derzeit gehen alle die meisten von letzterem aus. Die Folgen wären, wie gesagt, übersichtlich wenn das stimmt. Dafür müssten wir nur zeigen, dass es in \(NP\) Probleme gibt, die definitiv nicht deterministisch polynomiell lösbar, also nicht in \(P\) sind.

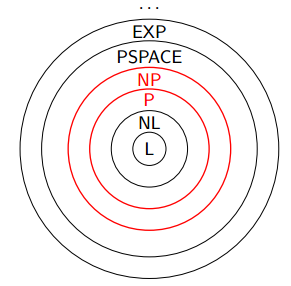
Graphisch aufgearbeitet sieht die hier beleuchtete, problematische Beziehung zwischen \(P\) und \(NP\) so aus:

Entnommen aus den Folien der TUM.

Und welche Möglichkeiten haben wir nun um \(P=NP\) oder \(P\neq{NP}\) zu beweisen?

1. Konstruktiver Beweis

   Wir finden einen polynomiellen Algorithmus, der ein \(NP\)-Vollständiges Problem polynomiell löst. Die Vollständigkeit ist wichtig, so dass wir diesen Algorithmus auch auf alle anderen aus \(NP\) reduzieren können müssen um die Klasse komplett abzudecken.

   Schaffen wir es also z.B. \(TSP\) deterministisch polynomiell zu lösen, haben wir – da \(TSP\) eben \(NP\)-vollständig ist, nichts geringeres als \(P=NP\) bewiesen.

2. Nicht-konstruktiver Beweis

   Nicht-konstruktiv bedeutet, dass man keine konkrete Lösung angibt, aber eindeutig auf die Existenz einer Lösung schließen kann.

   Man kann hier auch einen indirekten Beweis führen, indem man annimmt, es gäbe keine Lösung und diesen Satz zu einem Widerspruch führt. Daraus kann man dann schließen, dass es eine Lösung geben muss. Aber welche das ist, wird nicht genannt.

Also an die Arbeit 😉

Ich hoffe, ich konnte euch die Beziehung zwischen \(P\) und \(NP\) in diesem Beitrag etwas deutlicher machen.

Wie immer: Bei Ungenauigkeiten, ab in die Kommentare.

Update: Schnitzer im Projektionssatz aufgefallen. Fixed.

Als ich die letzten Beiträge zu Kurseinheit 5 von TIA durchgegangen bin, ist mir aufgefallen, dass einige Beweise doch noch nicht so nachvollziehbar sind, wie ich das gerne hätte.

Nach dem Editieren kam ich auf eine Seitenzahl von über 20. Schon wieder. Da blieb mir also nichts anderes übrig, als den Beitrag zu KE6 erneut zu trennen. Schwierigkeiten machten mir aber die Kommentare zu den Lernzielen als alles noch ein einzelner Beitrag war. Diese zu verschieben war ohne manuellen Eingriff in die Datenbank nicht möglich.

Solltet Ihr daher auf Kommentare treffen, die nicht unbedingt zu dem Beitrag hier passen: meine Schuld. Sie gehören dann zu einem der drei anderen.

Dieser Artikel ist brandneu und die anderen Beiträge zu KE6 sind teilweise massiv überarbeitet worden. Eine erneute Lektüre könnte sich also lohnen wenn Ihr bei KE6 der theoretischen Informatik A noch strauchelt und den Sachverhalt gerne mal in anderen Worten gelesen hättet.

Lange Rede, kurzer Sinn: Das sind also die Beiträge zu Kurseinheit 6.

• TIA: Rekursive und rekursiv-aufzählbare Mengen (Lernziele KE6, 1/4)
• TIA: Bild- und Projektionssatz (Lernziele KE6 2/4)
• TIA: Halte- Äquivalenz- und Korrektheitsproblem, Reduzierbarkeit, Satz von Rice (Lernziele KE6, 3/4)
• TIA: Gödel’scher Unvollständigkeitssatz (Lernziele KE6, 4/4)

Dieser dreht sich komplett um den Bild- und Projektionssatz. Ursprünglich war er nicht einmal eine halbe Seite lang. Als ich den Beweis dann Schritt für Schritt nachvollzog, wuchs er auf die aktuelle Größe heran. Tja, und da ist er nun.

Lernziel 5

Charakterisierung der r.a. Mengen durch Bild- und Projektionssatz

Die Charakterisierung ist wie folgt definiert:

1. \(A \subseteq \mathbb{N}\) ist r.a. gdw. \( A = \emptyset\) oder \(A = Bild(g)\) für ein \(g \in R^{(1)}\)

2. \(A \subseteq \mathbb{N}^k\) ist r.a. gdw. es eine rekursive Menge \(B \subseteq \mathbb{N}^{k+1}\) gibt mit \(A = \{x \in \mathbb{N}^k \mid (\exists t)(x,t) \in B\}\)

Nr. 1 bedeutet, dass eine Menge \(A\) dann rekursiv ist, wenn sie von einer totalen, rekursiven Funktion \(g\) aufgezählt werden kann, d.h. dass \(A\) Bild dieser Funktion ist.

Nr. 2 ist der Projektionssatz: eine Menge ist r.a. wenn sie die Projektion einer rekursiven Menge ist. Das Bild im Skript ist relativ eindeutig wenn man weiß, nach was man schauen muss. Ich nehme hierzu ein konkretes Beispiel mit \(k=1\) und der Menge \(B = \{(1,4),(1,2),(3,3),(3,2),(3,1),(5,1),(6,1)\}\), welche aus \(7\) Tupeln besteht.

Wir haben also zwei Achsen, die wir wie in der Definition \(t\) und \(x\) nennen. So sieht es dann aus:

Das Bild ist angelehnt an das aus dem Skript, nur mit einer Sonne, die ich gleich erkläre. Im Skript steht

„Die Projektion ist der eindimensionale Schatten bei der Beleuchtung von oben“.

Wir machen aus unserem \(2\)-Tupel nun ein \(1\)-Tupel: Uns interessieren nur die \(x\)-Werte aus den Tupeln, und so kommen wir auf die 2. x-Achse im Bild für unser \(A = \{(1),(3),(5),(6)\}\) . Das ist unsere vorderste Front.

Der Projektionssatz sagt also aus:

War unsere Menge \(B\) rekursiv (entscheidbar), so ist unsere Projektion \(A\) rekursiv aufzählbar (r.a.). Die Umkehrrichtung gilt auch: Ist unsere Projektion r.a., so ist die Menge \(B\) entscheidbar.

Aber beweisen wie diese Aussagen zunächst:

1. Teilbeweis zu Nr. 1: \(A\text{ ist r.a.}\Rightarrow{A=\emptyset}\) oder \(A=Bild(g)\) mit \(g\in R^{(1)}\).

Das ist umgangssprachlich am besten so auszudrücken: eine leere Menge \(A=\emptyset\) ist der Definition nach immer rekursiv/entscheidbar. Also Auch immer rekursiv aufzählbar/semi-entscheidbar. Hier gibt es für uns nichts weiter zu beweisen.

Ansonsten gilt: wenn die Menge durch eine totale Funktion aufgezählt werden kann, so ist diese Menge rekursiv-aufzählbar/semi-entscheidbar. Das ist leicht einzusehen: Semi-Entscheidbarkeit einer Menge \(A\) bedeutet ja, dass für für jedes Element aus \(A\) immer einen positiven (oder negativen, aber nicht beides gleichzeitig) Bescheid bekommen und somit auch \(A\) tatsächlich die Bildmenge der Funktion ist, die sie entscheidet: nämlich \(g\) ist.

Haben wir z.B. die Gesamtmenge der Instanzen für das Post’sche Korrespondenzproblem und wollen wir daraus die Menge der lösbaren Instanzen konstruieren, so können wir für jedes Element der Gesamtmenge die Funktion \(g\) laufen lassen, die es in jedem Fall positiv entscheidet wenn eine Lösung dafür gefunden wurde (dass wir das können, haben wir im letzten Beitrag schon gezeigt) und somit jedes Element aus der Menge \(A\), der Menge der gelösten Probleminstanzen, aufzählen.

Genau diese Definition begründet den Namen Art von Mengen: sie werden von \(g\) aufgezählt und sind damit rekursiv aufzählbar.

Das war der erste Teil. Kommen wir nun zum Umkehrschluss.

2. Teilbeweis zu Nr. 1: \(A\text{ ist r.a.}\Leftarrow{A=\emptyset}\) oder \(A=Bild(g)\) mit \(g\in R^{(1)}\).

Fall 1: \(A=\emptyset\): Wir nehmen an, dass die \(A\) leer ist. Nun suchen wir eine Funktion \(d\), die für alle Eingabewerte \(n\) kein Ergebnis liefert und setzen \(A\) als Definitionsmenge dieser Funktion \(d\): \(A=Def(d)\). Damit haben wir den ersten teil gezeigt.

Fall 2: Nun nehmen wir eine totale Funktion \(g\) und setzen \(A\) als Bildmenge von \(g\): \(A=Bild(g)\). Jetzt kommt unser \(f\) ins Spiel:

\(f(y)=\mu{x}[g(x)=y]\)

Was macht \(f\)? Es gibt uns für einen Eingabewert \(y\) das kleinste \(x\), wo gilt, dass der Funktionswert von \(g\) bei der Eingabe von \(x\) genau \(y\) ist.

Man mache sich hier klar, dass egal, was \(g\) als Eingabewert bekommt, wir immer \(div\) zurückbekommen (denn die leere Menge \(A\) ist die Bildmenge von \(g\)).

\(f\) kann im Gegenzug alle Werte aus \(\mathbb{N}\) bekommen und auf alle abbilden. Diese Funktion ist offensichtlich berechenbar.

Das bedeutet: für ein \(y\in{Def(f)}\) gibt es auch ein \(x\) mit \(g(x)=y\). Da \(y\in{Bild(g)}\) ist, gilt: \(Def(f)=Bild(g)\) und \(Bild(g)\) ist somit rekursiv aufzählbar.

Und das war der zweite Teil.

1. Teilbeweis zu Nr. 2: \(A\text{ ist r.a.}\Rightarrow{B}\text{ rekursiv}\)

Zeigen wir zunächst den umgekehrten Weg von Punkt 2 mit: \(A\text{ ist r.a.}\Rightarrow{B}\text{ rekursiv}\). Dafür gehen wir davon aus, dass eine Menge \(A\subseteq\mathbb{N}^k\) rekursiv aufzählbar ist:

• Dann gibt es eine Gödelnummer \(i\) für ein \(x\in{A}\) mit \(\varphi_i(\pi^{(k)}(x))\) existiert.

Es gibt also eine Maschine mit der Nr. \(i\), die uns zum Element \(x\) eine Ausgabe beschert. Die Cantorsche Tupelfunktion \(\pi\) ist hier nur dazu da um eine evtl. Mehrstelligkeit \(k\) der Eingabe für die Maschine auf eine Stelle herunterzurechnen.

• Gibt es die Maschine mit der Nr. \(i\), so gibt es auch selbstverständlich die dazu gehörige Schrittzahlfunktion \(SZ\), die im \(\Phi\)-Theorem benutzt wird: \(\Phi_i(\pi^{(k)}(x))\)

Kennen wir alles schon: das ist die Anzahl der Schritte, die \(\varphi_i\) bei der Eingabe von \(x\) braucht um zum Ende zu gelangen. Da die Menge \(A\) rekursiv aufzählbar ist, existiert für jedes \(x\in{A}\) diese Rechenzeitfunktion \(\Phi_i(x)\).

• Und damit gilt: \((\exists{t})\Phi_i(\pi^{(k)}(x))\leq{t}\)

Es gibt also ein kleinstes \(t\), d.h. die minimale Anzahl der Schritte, die die Maschine \(\varphi_i\) bei der Eingabe von \(x\) rechnet um bis zum Ergebnis zu gelangen. Es gibt aber auch noch mehr \(t’s\). Eben die, die kleiner sind als die maximale Schrittzahl, die die Maschine bei der Eingabe von \(x\) rechnet um bis zur HALT-Marke zu gelangen.

• Nun definieren wir die Menge \(B=\{(x,t)\mid\Phi_i(\pi^{(k)}(x))\leq{t}\}\)

Die Paare sind also die Eingabe \(x\) für die Maschine \(\varphi_i\) und \(t\) die Anzahl der Schritte, die die Maschine bis zum Ergebnis rechnen könnte. Sagen wir z.B. die Maschine rechnet bei der Eingabe von \(x\) genau \(5\) Schritte bis sie an der \(HALT\)-Marke ankommt, so kann \(t\leq{5}\) sein. In der Menge \(B\) würde daher \((x,1)(x,2)(x,3),(x,4),(x,5)\) liegen.

• Nach dem \(\Phi\)-Theorem ist diese Menge \(B\) also entscheidbar.

Das sollte klar sein: das Paar \((x,t)\), also die Eingabe \(x\) und die Rechenzeit \(t\) ist entscheidbar, da wir für jedes \(x\) (wenn es in der Menge \(A\) ist) immer einen Ausgabewert haben, ist auch die maximale Schrittzahl immer gegeben. Wir können entscheiden ob die Maschine bei der Eingabe von \(x\) nach \(t\) Schritten hält oder nicht.

Anders ausgedrückt: Wir können fragen: „Hey, gilt \((x,5)?\) und \(\Phi\) prüft ab ob bei der Eingabe von \(x\) die Maschine innerhalb von \(5\) Schritten zum Ergebnis kommt und kann dann sagen „Ja, das geht!“ oder „Nein, ging nicht!“. Diese Menge ist also Entscheidbar.

Der eine Weg von Punkt 2 ist damit gezeigt.

2. Teilbeweis zu Nr. 2: \({A}\text{ ist r.a.}\Leftarrow{B}\text{ rekursiv}\)

Und nun die andere Richtung: \({A}\text{ ist r.a.}\Leftarrow{B}\text{ rekursiv}\). Sei \(B\subseteq\mathbb{N}^{k+1}\) also rekursiv/entscheidbar.

• Setzen wir die Menge \(A=\{x\in\mathbb{N}^k\mid{}(\exists{t} (x,t)\in{B}\}\)

\(B\) ist, wie wir wissen ja entscheidbar. Zu einer Eingabe erhalten wir (wenn sie zu einer r.a. Menge gehört) auch eine maximale Rechenzeit und können so prüfen ob sie \(t\) entspricht oder größer/kleiner ist. Hier ist \(A\) also die Menge der Eingaben, d.h. die ersten Elemente aus den Tupeln von \(B\), die aus Eingabe \(x\) und zugehörigem Wert für eine angenommene Rechenzeit \(t\) bestehen.

• Nun definieren wir unsere „Projektionsfunktion“ durch

\(f(x):=\mu{t}[cf_B(x,t)=1]\)

Was tut \(f\)? Zunächst fragen wir uns, was tut \(cf_B\)? Das ist die (volle) charakteristische Funktion für die Menge \(B\). Sie gibt uns eine \(1\) zurück wenn die Maschine bei der Eingabe von \(x\) nach maximal \(t\) Schritten hält.
Und \(\mu{t}\)? Sie gibt uns das kleinste \(t\) zurück, d.h. die minimalste Anzahl an Schritten, die benötigt werden um bei der Eingabe von \(x\) von der Maschine eine Ausgabe zu erhalten, denn in unserer menge \(B\) liegen ja durchaus mehrere Kombinationen von \((x,t)\) mit den unterschiedlichsten \(t’s\).

Mit \(f(x)\) bekommen wir das also für die Eingabe \(x\) kleinste \(t\).

Der Definitionsbereich von \(f\) sind somit alle Elemente aus \(A\) und \(A\) damit rekursiv aufzählbar.

Done.

Exkurs: den Unterlagen der Uni Düsseldorf kann man den Projektionssatz auch mit einer anderen Menge \(B\) beweisen, z.B. mit \((x,z)\) (wobei \(x\) die Eingabe und \(z=\pi(y,t)\) das durch die Tupelfunktion \(\pi\) auf ein Element \(z\) zurückgeführte Paar aus Ausgabe \(y\) und Schrittzahl \(t\) ist) wenn \(T_i(x,t)\) (auch Turingprädikat genannt) erfüllt ist.

Das Turingprädikat ist genau dann erfüllt wenn Maschine \(T_i\) bei der Eingabe von \(x\) nach \(t\) Schritten mit einer Ausgabe \(y\) hält.

Im Endeffekt also nur ein kleines Upgrade unserer Menge \(B\).

Fassen wir die Ergebnisse zusammen, kommen wir so zu unserer Antwort zum Lernziel.

Antwort zum Lernziel: Der erste Teil des Projektionssatzes ist der Grund für den Begriff  „rekursiv-aufzählbar“ für eine Menge \(A\). Diese ist genau dann rekursiv-aufzählbar wenn ihre Elemente von einer totalen Funktion \(g\) aufgezählt werden können, es gilt damit \(A=Bild(g)\) und \(A\) ist r.a.

Der zweite Teil ist die Projektion, die aus den Eingabewerten \(x\) einer r.a. Menge \(A\) besteht. Da diese positiv beschieden sind, gibt es auch die zugehörige Anzahl an Schritten, die die Maschine für den positiven Bescheid brauchte. Setzen wir in den Tupeln \((x,t)\) das Element \(t\) auf Werte, die höher sind als die Schrittzahlfunktion der Maschine bei der Eingabe \(x\), so haben wir in der Menge \(B\) mehrere Tupel der Form \((x,t)\) mit festem \(x\) und variablem \(t\).

Aus diesen Elementen der Menge \(B\) bilden wir die \(x\)– und \(y\)-Achse unserer Grafik. Diese Wertekombinationen aus \(x\) und \(t\) sind entscheidbar (ich kann entscheiden ob ich zu einer positiven Eingabe \(x\) mehr als \(t\) Schritte brauche oder nicht). Das ist der Weg von einer rekursiv-aufzählbaren Menge \(A\) zu einer entscheidbaren \(B\).

Auch der Rückweg gilt: aus der Menge \(B\) mit den Elementen \((x,t)\) kann ich mir meine Eingabewerte \(x\) wieder rausholen, indem ich mich nur für das kleinste \(t\) interessiere (die Minimierungsfunktion). Damit „blende“ ich alle anderen Kombinationen mit größerem \(t\) einfach aus. Das ist die Projektion.

Merksatz: Eine Menge ist rekursiv aufzählbar wenn sie die Projektion einer entscheidbaren Menge ist.

Weiter geht es im nächsten Beitrag zum Halte- Äquivalenz- und Korrektheitsproblem, Reduzierbarkeit und Satz von Rice