Kategorie: Theoretische Informatik

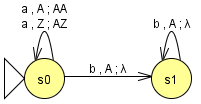
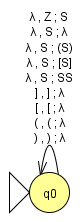Update: Fehler im Automaten behoben.

Letzter Beitrag zum Thema… ich tippe besonders langsam, versprochen 😉

Lernziel 5

Was sind determinierte Kellerautomaten?

Wir könnten zwar mit nichtdeterministischen Kellerautomaten leben und würden es sogar. Aber es gibt da ein Problem: wir können sie technisch nicht realisieren.

Den determinierten Kellerautomaten hatten wir im vorherigen Beitrag auch bereits definiert. Uns interessiert deshalb nicht was sie sind, sondern vielmehr wie sie sich von nichtdeterministischen Kellerautomaten unterscheiden und was das für Auswirkungen auf die erkannte Sprachklasse hat.

Eine echte Teilmenge der von nichtdeterminierten Kellerautomaten erkannten, kontextfreien Sprachen ist die deterministische kontextfreie Sprache:

Deterministisch kontextfrei

Eine Sprache ist deterministisch kontextfrei wenn es einen determinierten Kellerautomaten gibt, der sie erkennt.

Das Erkennen bedeutet folgendes:

Wenn \(L\subseteq\Sigma^{*}\) eine deterministisch kontextfreie Sprache ist, dann gibt es einen Kellerautomaten \(A=(\Sigma,\Gamma,\$,Q,q_0,\{q_{+}\},\delta)\) mit einem Zustand \(q_{-}\in Q\), so dass für alle Worte \(\omega\in\Sigma\) gilt:

\(\omega\in L\Leftrightarrow (q_0,\omega\$,\$)\vdash^{*}(q_{+},\$,\epsilon)\)

Das Wort \(\omega\) ist Teil der deterministisch kontextfreien Sprache wenn es eine Überführungsfolge im Automaten \(A\) gibt, die ausgehend vom Anfangszustand in einen akzeptierenden Endzustand mündet und die Eingabe zu Ende gelesen wurde, wobei der Keller leer ist.

\(\omega\notin L\Leftrightarrow (q_0,\omega\$,\$)\vdash^{*}(q_{-},\$,\epsilon)\)

Das Wort \(\omega\) ist nicht Teil der deterministisch kontextfreien Sprache wenn es eine Überführungsfolge im Automaten \(A\) gibt, die ausgehend vom Anfangszustand in einen nicht-akzeptierenden Endzustand mündet und die Eingabe zu Ende gelesen wurde, wobei der Keller leer ist.

Sie ist zudem auch noch eindeutig:

Jede deterministisch erkannte Sprache ist eindeutig*.

* erinnert Ihr euch noch an die Eindeutigkeit? Fall nicht: jedes abgeleitete Wort einer eindeutigen Sprache/Grammatik hat nur einen einzigen Ableitungsbaum.

Wir zeigen gleich, dass die deterministischen Automaten weniger leistungsfähig sind. Folgende Überlegungen sind notwendig:

1. ein deterministischer Kellerautomat akzeptiert nur Worte, die er zu Ende liest. Wir müssen daher unseren deterministischen Automaten entsprechen ummodellieren und die Szenarien vermeiden, wo der Automat nicht weiterlesen kann:

a) Keller leer bevor Eingabe zu Ende.

Lösung: neues Keller-Leerheits-Zeichen, dass nie gelöscht wird.

b) keine Folgekonfiguration für aktuelle Konfiguration vorhanden

Lösung: Vervollständigen von \(\delta\), so dass wir zu jeder Möglichkeit einen Folgezustand haben

c) das Erreichen eines Zyklus, wo der Kopf nicht bewegt wird

Lösung: Erkennen und vermeiden des Zyklus.

2. Wir haben einen ausgezeichneten, positiven Endzustand: entweder er akzeptiert das Wort und wir landen in \(q_{+}\) oder nicht und wir landen in \(q_{-}\in Q\).

Mit der Vorarbeit aus dem letzten Beitrag, ist es nicht schwer diese weiteren Einschränkungen nachzuvollziehen.

Der Beweis für die Komplementbildung gelingt durch simples Vertauschen der Zustände \(q_{+}\) und \(q_{-}\), so dass wir diese Eigenschaft zusammenfasen können:

Sei \(L\subseteq\Sigma^{*}\) deterministisch kontextfrei, so ist es auch \(\Sigma^{*}\setminus L\).

Antwort zum Lernziel: Kellerautomaten (PDAs) sind endliche Automaten, die durch einen Kellerspeicher erweitert wurden. Bei einem Kellerautomaten wird ein Wort dann erkannt wenn der Keller leer ist oder der Automat in einem Endzustand landet (oder beides gleichzeitig).

Für einen determinierten Kellerautomaten gilt zudem, dass es für jedes Eingabezeichen und jedes oberste Kellerzeichen nur einen Zustandsübergang gibt, so dass der Kellerautomat den Berechnungsweg nicht zufällig wählen kann. Ist das nicht der Fall und gibt es zu einem Eingabezeichen und einem obersten Kellerzeichen mehrere mögliche Folgezustände, so ist der Kellerautomat nichtdeterministisch.

Für eine deterministisch kontextfreie Sprache \(L\) bedeutet es, dass wir in jedem Fall für ein Wort \(\omega\in L\) nach endlich vielen Schritten die Endkonfiguration \((q_{+},\$,\epsilon)\) (ausgewiesener Endzustand, Ende der Eingabe, leerer Keller) oder für ein Wort \(\omega\notin L\) \((q_{-},\$,\epsilon)\) (beliebiger Zustand aus \(Q\), Ende der Eingabe, leerer Keller) erreichen.

 

Lernziel 6

Ist jede kontextfreie Sprache deterministisch? Mit Begründung!

Ein (für mich) etwas verständlicheres Beispiel habe ich in den Folien der HU-Berlin gefunden und würde das hier gerne anbringen. Nehmen wir zwei deterministisch kontextfreie Sprachen (DCFL), die von einem determinierten Automaten erkannt wird, z.B.

\(L_1=\{a^i b^j c^k\mid i\neq j\}\in DCFL\) sowie

\(L_2=\{a^i b^j c^k\mid j\neq k\}\in DCFL\).

Beide Sprachen sind deterministisch kontextfrei. Wir können also einen deterministischen Kellerautomaten angeben, der sie erkennt.

Um \(L_1\) zu entscheiden, können wir uns z.B. darauf beschränken die \(a’s\) einzulesen, \(A’s\) in den Keller zu schreiben und anschließend die \(b’s\) einzulesen und die \(A’s\) aus dem Keller zu entfernen. Es sind drei Fälle zu unterscheiden:

1. Gab es weniger \(a’s\) als \(b’s\), so haben wir noch \(b’s\) auf dem Eingabeband, während der Keller bereits leer ist und alles ist gut.

2. Gab es mehr \(a’s\) als \(b’s\), so haben wir keine \(b’s\) auf dem Eingabeband, während noch \(A’s\) im Keller sind und alles ist immernoch gut.

3. Gab es die gleiche Anzahl \(a’s\) und \(b’s\), so haben wir einen leeren Keller just in dem Moment, wo wir keine \(b’s\) auf dem Eingabeband haben und das Wort wird abgelehnt.

Das gleiche Verfahren klappt auch mit \(L_2\) (nur mit \(b’s\) und \(c’s\) statt mit \(a’s\) und \(b’s\)).

Schauen wir uns doch eine weitere Sprache an:

\(L_1\cup L_2 = \{a^i b^j c^k\mid i\neq j\) oder \(j\neq k\}\in CFL\setminus DCFL\).

Wie man sieht, ist das eine Vereinigung der beiden Sprachen \(L_1\) und \(L_2\). Um das etwas anschaulicher zu machen, schauen wir uns die Mengen doch einmal mit \(1\leq i,j,k\leq 2\) an:

\(L2_1=\{abbc,abbcc,aabc,aabcc\}\)

\(L2_2=\{abcc,abbc,aabcc,aabbc\}\)

\(L2_1\cup L2_2 = \{abbc,abbcc,aabc,aabcc,abcc,aabbc\}\)

Während wir für für \(L2_1, L2_2\) und die Vereinigung der beiden Sprachen \(L2_1\cup L2_2\) sogar einen endlichen Automaten angeben können, der sie erkennt (wir erinnern uns: das ist genau der Grund warum alle endlichen Sprachen sogar regulär sind, ein akzeptierender Zustand pro Wort reicht im endlichen Automaten aus um die Sprachen zu erkennen), gelingt es uns bei \(i,i,k\in\mathbb{N}\) nur für \(L_1\) sowie \(L_2\) einen Kellerautomaten anzugeben, der die Sprache erkennt (wir müssen die Anzahl der Buchstaben beobachen können und können das nur mindestens mit einem Kellerautomaten. Mindestens weil Turingmaschinen als stärkstes Berechnungsmodell selbstverständlich auch gehen, denn sie können ja selbst Typ-0-Sprachen erkennen).

Weit mehr Probleme macht uns die Vereinigung! Das Problem mit ihr ist: sie ist zwar kontextfrei, aber nicht deterministisch kontextfrei. Denn dafür können wir keine deterministische Kellermaschine angeben, sie sie erkennt.

Woran liegt das? Wie wir oben gesehen haben, beobachten wir mit dem Keller nur eine Variable (die Anzahl unserer ersten, eingelesenen Buchstaben) und können so eine andere abhängig von dieser entscheiden. Das ist bei den Sprachen \(L_1\) und \(L_2\) ja kein Problem. Bei \(L_1\cup L_2\) haben wir jedoch drei Variablen, die von einander abhängig sind. Denn wir müssen \(j\) in Abhängigkeit von \(i\) und \(k\) in Abhängigkeit von \(j\) prüfen. Das war’s also mit dem Determinismus, denn wir haben mehrere Wege, die wir beschreiten müssen um am Ende einen zu finden, der funktioniert.

Die kontextfreie Grammatik für \(L_1\cup L_2\) ist:

\(S\rightarrow{DC \mid AE \mid B}\)

\(D\rightarrow{F\mid G}\) \(F\rightarrow{aF \mid aFb \mid a}\) \(G\rightarrow{Gb \mid aGb\mid b}\) \(C\rightarrow{cC\mid\epsilon}\)

\(A\rightarrow{aA\mid\epsilon}\)

\(E\rightarrow{H\mid I}\) \(H\rightarrow{bH\mid bHc\mid b}\) \(I\rightarrow{Ic \mid bIc \mid c}\)

\(B\rightarrow{J \mid K}\)

\(J\rightarrow{aJ\mid aJc\mid aL}\) \(K\rightarrow{Kc\mid aKc\mid Lc}\) \(L\rightarrow{bL\mid\epsilon}\)

Und daraus können wir den zugehörigen Automaten nach dem Schema aus dem vorherigen Beitrag bauen:

Download: AiBjCk_NPDA_JFLAP-Datei

Damit haben wir auch eine wesentliche Aussage für das nächste Lernziel herausgearbeitet: dass wir keinen deterministischen Automaten für \(L_1\cup L_2\) angeben können liegt daran, das die deterministisch kontextfreien Sprachen zwar abgeschlossen sind bzgl. Schnitt und Komplement, aber nicht gegen Vereinigung, Durchschnitt, Spiegelung und Konkatenation! Und das obere Beispiel war die Vereinigung. Beispiele für Durchschnitt, Spiegelung und Konkatenation überlasse ich erstmal euch 😉

Zusammengefasst: Wir haben mit dem deterministischen Kellerautomaten, welche die Sprache erkennt, tatsächlich eine Beschneidung der Möglichkeiten, die uns ein nichtdeterministischer Kellerautomat bietet: wir können nicht mehr zwischen Berechnungspfaden wählen und sind an unsere Wahl „gebunden“. War sie falsch, so landen wir in einer Sackgasse und damit war es das. Bei einem nichtdeterministischen Automaten haben wir währenddessen (durch mehrere Folgekonfigurationen für eine Konfiguration) bereits andere Wege parallel beschritten, wo uns einer (wenn wir einen korrekten Automaten angegeben haben) schon zur Lösung führen wird. War eine Berechnung falsch, so landen wir auf diesem einen Weg in einer Sackgasse und … es ist uns egal. Wir haben ja noch genug andere Wege, die wir parallel beschreiten.

Hauptsache wir können beweisen, dass min. einer dieser Wege zu einem Ergebnis führt und entscheidet ob ein Wort sich in der Sprache befindet. Tut es das nicht, kann der nichtdeterministische Automat von uns aus solange weiterrechnen, bis er schwarz wird.

Ein Blick aus einer anderen Brille: Um bei der Sprache \(L_1\cup L_2\) entscheiden zu können ob ein Wort tatsächlich zur Sprache gehört oder nicht, ist der Algorithmus wirklich einfach: Wir zählen die \(a’s\), \(b’s\) und \(c’s\), speichern die Anzahl auf dem Hilfsband und vergleichen die drei Variablen nachdem wir die Eingabe vollständig eingelesen haben miteinander. Ihr habt sicher schon eine TM im Kopf, die das macht. Während wir das also mit einer DTM problemlos machen können, schaffen wir das mit einem PDA durch die Einschränkungen leider nicht.

Antwort zum Lernziel: Nicht jede kontextfreie Sprache ist deterministisch. Es gibt kontextfreie Sprachen, die aufgrund ihrer Struktur nicht von einem PDA erkannt werden können weil ihr Aufbau von mehreren Variablen abhängt, diese jedoch nicht durch einen einzigen Kellerspeicher deterministisch abgebildet werden können. Erst durch das Beschreiten mehrerer Berechnungspfade ist es möglich auch mehrere Variablen in die Betrachtung einzubeziehen und aus der so generierten Vielzahl an Pfaden die Aussage zu treffen, dass einer in jedem Fall zum Ziel führt wenn das Wort sich in der Sprache befindet.

Eine solche kontextfreie, aber nicht deterministische Sprache lässt sich durch Vereinigung, Konkatenation, Durchschnitt oder Spiegelung einer oder mit mehreren deterministisch kontextfreien Sprachen erzeugen, da die Sprachklasse der deterministisch kontextfreien Sprachen nicht abgeschlossen gegen diese Operationen ist.

Lernziel 7

Sind die kontextfreien bzw. deterministisch kontextfreien Sprachen abgeschlossen unter Vereinigung, Durchschnitt, Komplement und Schnitt mit regulären Mengen?

Was soll ich hier schreiben? Reicht die Tabelle aus dem Skript? 😉 Ihr solltet euch noch einmal vor Augen führen, wie die Sprachklassen zusammenhängen und die Beziehungen zwischen Unter- und Oberklasse sind. Dann wird euch auch deutlich warum diese gegen gewisse Operationen nicht abgeschlossen sein können. Vielleicht schreibe ich später noch ein paar Sätze dazu, aber bis dahin:

Antwort zum Lernziel:

	kontextfrei	deterministisch
Vereinigung	+	–
Durchschnitt	–	–
Komplement	–	+
Konkatenation	+	–
Stern	+	–
Schnitt mit regulären Mengen	+	+

Lernziel 8

Welche der folgenden Probleme sind für kontextfreie Grammatiken entscheidbar/unentscheidbar? Wortproblem, Endlichkeitsproblem, Leerheitsproblem?

Hier sollten wir einige Probleme auf den Mengen entscheiden können, diese sind:

• Wortproblem: ob sich ein Wort \(\omega\) in der Sprache \(L\) befindet (oder nicht).
• Inklusion: ob die Worte einer Sprache \(L_1\) in einer anderen Sprache\(L_2\) enthalten sind
• Äquivalenz: ob die Sprache \(L_1\) die gleiche Sprache wie \(L_2\) ist.
• Leerheit: ob die Sprache leer ist, d.h. wir können mir der Grammatik, die die Sprache erzeugt keine Wörter erzeugen. Achtung: jede leere Sprache ist regulär.
• Endlichkeit: ob die Sprache endlich ist (endliche Sprache = reguläre Sprache = endlicher Automat)
• Universalität: ob die Sprache alle Kombinationen der Elemente aus dem Alphabet \(\Sigma\) umfasst
• Eindeutigkeit: ob es für ein Wort nur einen Ableitungsbaum gibt.
• Determiniertheit: es gibt einen deterministischen Kellerautomaten, der entscheidet ob \(\omega\) zur Sprache gehört oder nicht.

Antwort zum Lernziel:

	kontextfrei	deterministisch
Wortproblem	+	+
Inklusion	–	–
Äquivalenz	–	+
Leerheit	+	+
Endlichkeit	+	+
Universalität	–	+
Eindeutigkeit	–	+
Determiniertheit	–	+

Damit haben wir auch die letzte Kurseinheit durch. Hoffentlich konntet Ihr etwas mit den Zusammenfassungen anfangen und es haben sich keine Fehler eingeschlichen. Wenn doch: ab damit in die Kommentare!

Update 2: Einzel- und Mehrschrittrelationen, sowie Überführungsfunktion genauer erklärt.

Großes Update: Fehlerbeseitigung und langes Beispiel zum Beweisverfahren Sprache zu Automat(en) zu Grammatik zu Sprache (Lernziel 4).

Lernziel 3

Wie sind Kellerautomaten und die von ihnen akzeptierte Sprache definiert?

Noch einmal zur Auffrischung: alle Sprachen, die ein endlicher Automat akzeptiert sind regulär. Haben wir aber eine nicht reguläre Sprache, von was wird sie dann akzeptiert? Ein schönes Beispiel gab es (schon wieder) im Buch von Dirk W. Hoffmann mit der Sprache:

\(LC_2=\{a^n b^n\mid n\in\mathbb{N}\}\)

Wir brauchen also einen Automaten, der unsere Sprache akzeptiert. Mit dem Pumping Lemma für reguläre Sprachen sehen wir sofort, dass sie nicht regulär ist. Auch wenn wir es versuchen, so gelingt es uns nicht einen endlichen Automaten für diese Sprache zu bestimmen. Wir schaffen das immer nur für eine endliche Teilmenge der Sprache (durch akzeptierende Zustände für jedes Wort aus der Sprache) und wir wissen ja, dass jede endliche Sprache auch regulär ist weil wir im schlimmsten Fall einfach nur einen akzeptierenden Zustand für jedes Wort bauen müssen. Zwar ist das bei einer endlichen Teilmenge unserer Sprache \(LC_2\) nicht notwendig; der endliche Automat kommt nur mit einem akzeptierenden Zustand aus, das Prinzip sollte aber klar geworden sein. Jeder akzeptierende Zustand fungiert also als eine Art „Speicher“.

Was müssen wir also tun um einen Automaten zu bekommen, der diese Sprache akzeptiert? Wir müssen uns irgendwo die Anzahl der \(a’s\) merken und sie mit der Anzahl der \(b’s\) vergleichen können. Wir brauchen also irgendeinen „unendlichen“ Speicher, da wir ja auch etvl. ein unendlich langes Wort haben. Hier helfen uns die Zustände unseres endlichen Automaten nicht weiter, denn er ist… nunja… endlich. 😉

Wir erweitern unseren endlichen Automaten einfach, so dass wir noch genau die kontextfreien Sprachen mit ihm akzeptieren/semi-entscheiden können.

Während in der Literatur häufig mit einem \(5\)-Tupel gearbeitet wird, hat das Skript eigene Vorstellungen und verwendet ein \(7\)-Tupel zur Definition eines Kellerautomaten. Zusätzlich zu den üblichen Dingen werden auch noch das Kellerstartsymbol \(\\)$ und die Menge der Endzustände \(Q_f\) definiert. Ist vielleicht auch gar nicht schlecht, denn die Wikipedia sieht das ähnlich. Ich echauffiere mich also in den letzten Zügen des Skripts nicht über dasselbe. 😉 Wollen wir also formal definieren:

Kellerautomat

\(A=(\Sigma,\Gamma,\S,Q,q_0,Q_f,\delta)\) mit

\(\Sigma\) endliches Eingabealphabet

\(\Gamma\) endliches Kelleralphabet

\(\$\in\Gamma\setminus\Sigma\) Kellerstartsymbol und Markierung für Eingabeende

\(q_0\in Q\) als Anfangszustand

\(O_f\subseteq Q\Sigma\) Endzustände

\(\delta\) Zustandsübergangsfunktion

Kommen wir nun zur Zustandsübergangsfunktion \(\delta\). Ich würde sagen, dass ich ein paar Beispiele gebe anstatt vollständig formal zu bleiben:

\(\delta(s_0,a,A):=\{(s_1,B)\}\)

Im Zustands \(s_0\), lese \(a\) aus der Eingabe, nimm \(A\) vom Kellerstapel, wechsle in den Zustand \(s_1\) und schiebe \(B\) auf den Kellerstapel.

\(\delta(s_0,b,A):=\{(s_1,\epsilon)\}\)

Im Zustands \(s_0\), lese \(b\) aus der Eingabe, nimm \(A\) vom Kellerstapel, wechsle in den Zustand \(s_1\) und lege nichts in den Kellerstapel. Damit wurde das Zeichen \(A\) aus dem Keller gelöscht. Lag \(A\) zu diesem Zeitpunkt nicht auf dem Stapel, kann die Übergangsfunktion nicht angewandt werden.

\(\delta(s_0,\epsilon,\epsilon):=\{(s_0,\epsilon)\}\)

Im Zustands \(s_0\), lese nichts von der Eingabe, nimm nichts vom Kellerstapel, bleibe im Zustand \(s_0\) und lege nichts in den Kellerstapel. 

Mittels \(\vdash\) und \(\vdash^n\) sowie \(\vdash^{*}\) werden die Einzel- und Mehrschrittrelationen bezeichnet.

\((s_0,aaaa,AAA)\vdash(s_1,aaa,AA)\)

Vom Zustands \(s_0\) mit dem Wort \(aaaa\) auf dem Eingabeband und \(AAA\) im Keller, kann man in einem Schritt den Zustand \(s_1\) erreichen, wobei dann nur noch \(aaa\) auf dem Eingabeband und \(AA\) im Keller steht.

\((s_0,ababa,AAA)\vdash^5(s_1,aaaa,AAAA)\)

Vom Zustands \(s_0\) mit dem Wort \(ababa\) auf dem Eingabeband und \(AAA\) im Keller, kann man in \(5\) Schritten den Zustand \(s_1\) erreichen, wobei dann \(aaaa\) auf dem Eingabeband und \(AAAA\) im Keller steht.

\((s_0,bb,AB)\vdash^{*}(s_1,\$,\$)\)

Vom Zustands \(s_0\) mit dem Wort \(bb\) auf dem Eingabeband und \(AB\) im Keller, hat man nach dem letzten, möglichen Berechnungsschritt den Zustand \(s_1\) erreicht, wobei dann nichts auf dem Eingabeband und nichts im Keller steht.

Damit sind wir auch schon fast durch. Es gibt jedoch drei Dinge, die noch wichtig sind: der Automat hat zwei Wege eine Sprache zu erkennen

1. mittels Endzustand (wir landen in einem Endzustand)

Formal: \(L(A) =\{\omega\in\Sigma^{*}\mid\exists q\in Q_f \exists X\in\Gamma^{*} (q_0,\omega\$,\$)\vdash^{*}(q,\$,X)\}\)

„Für ein Wort über dem Alphabet \(\Sigma\)„, ausgehend vom Startzustand \(q_0\), während wir das Eingabewort und die Markierung für das Eingabeende auf dem Band haben (\(\omega\\)$) kommen wir nach endlich vielen Schritten zum Endzustand \(q\), während auf dem Eingabeband der Kopf über dem Eingabeende \(\\)$ ist und irgendwas (\(X\)) im Keller steht“

2. mittels leerem Keller (wir landen zwar nicht einem Endzustand, aber der Keller ist leer)

Formal: \(L(A) =\{\omega\in\Sigma^{*}\mid\exists q\in Q (q_0,\omega\$,\$)\vdash^{*}(q,\$,\epsilon)\}\)

„Für ein Wort über dem Alphabet \(\Sigma\)„, ausgehend vom Startzustand \(q_0\), während wir das Eingabewort und die Markierung für das Eingabeende auf dem Band haben (\(\omega\\)$) kommen wir nach endlich vielen Schritten zum beliebigen Zustand \(q\), während auf dem Eingabeband der Kopf über dem Eingabeende \(\\)$ ist und der Keller leer ist (\(\epsilon\))“

Und die Definition des Determinismus einer Kellermaschine:

Ein Kellerautomat ist determiniert, wenn:

es zu jedem Eingabezeichen und jedem obersten Kellerzeichen maximal ein Zustandsübergang gibt.

Antwort zum Lernziel: die Kellerautomaten bestehen aus einem Eingabe- und einem Kelleralphabet, einem Kellersymbol und der Markierung für das Eingabeende sowie Anfangs- und Endzuständen und der Zustandsübergangsfunktion. Die von ihnen akzeptierte Sprache wird definiert als die Worte, die a) den Automaten entweder in einen Endzustand bringen wenn das Ende des Eingabewortes erreicht ist, wobei egal ist, was im Keller steht oder b) der Keller leer ist wenn das Ende des Eingabewortes erreicht ist, wobei es egal ist, in welchem Zustand sich der Automat zu diesem Zeitpunkt befindet.

Und das sind genau die kontextfreien Sprachen, die die Typ-2-Grammatiken erstellen können. Wie wir zu einer kontextfreien Grammatik einen Kellerautomaten basteln, zeigen wir im nächsten Abschnitt, indem wir die Produktionsregeln der Grammatik in die Übergänge unseres Kellerautomaten codieren.

Lernziel 4

Wie zeigt man, dass Kellerautomaten genau die kontextfreien Sprachen erkennen?

Ich würde hier noch ein paar Kleinigkeiten in eure Erinnerung rufen bevor wir mit den Kellerautomaten richtig loslegen. Das liegt u.a. daran, dass wir bei den vorher betrachteten Sprachen eine Äquivalenz zwischen TM und NTM hatten (wir können eine NTM durch eine TM simulieren indem wir einfach alle möglichen Berechnungspfade der NTM durchlaufen), bei den Kellerautomaten hier aber strikt trennen müssen. Nichtdeterministische Kellerautomaten sind eben nicht äquivalent zu deterministischen. Letztere spielen aber eine große Rolle, so dass wir noch später auf sie zurück kommen werden.

Um also zu zeigen, dass ein Kellerautomat genau die kontextfreien Sprachen erkennt, müssen wir zu einer kontextfreien Grammatik \(G\) einen Kellerautomaten  \(A\) angeben, der mit seinen zwei Akzeptanzmethoden (leerer Keller und Endzustand) ein Wort \(\omega\) genau dann akzeptiert wenn das Wort mittels der kontextfreien Grammatik \(G\) abgeleitet werden kann. Es muss also gelten:

\(L(G) = L(A)\)

Um zu zeigen, dass wir alle kontextfreien Sprachen durch Kellerautomaten erkennen lassen können, müssen wir das Regelschema der kontextfreien Grammatiken in ein Zustandsübergangsschema für Kellerautomaten umwandeln. Nur ein Problem haben wir: Die Frage welche Ersetzung (d.h. die Rückumwandlung der Ableitung) zu machen ist, müssen wir beantworten und tun das mit unserem Nichtdeterminismus, indem wir aus mehreren in Frage kommenden Ersetzungen einfach eine raten!

Ich würde sagen, dass wir auch hier direkt mit einem Beispiel starten und eine kontextfreie Grammatik in einen Kellerautomaten überführen.

Grammatik zum Automat mit einem Zustand: kontextfreie Grammatik \(G_D=\{\Sigma,\Pi,R,S\}\) mit den Regeln \(R\)

\(S\rightarrow\epsilon\mid SS\mid [S]\mid(S)\)

soll überführt werden in einen Kellerautomaten \(K_{G_D}=(\Sigma,\Gamma,S,Q,q_0,Q_f,\delta)\), der die gleiche Sprache \(L(G_D)\) akzeptiert.

Ja, das ist die Dyck-Sprache. Geklaut aus dem Buch von Dirk W. Hoffmann. Sehr einfaches und leicht verständliches Beispiel. Wie kommen hier mit  nur einem Zustand aus und können den Kellerspeicher so effizient nutzen. Nun müssen wir erstmal \(\Sigma,\Gamma,S,Q,q_0,Q_f,\delta\) des Automaten festlegen.

Kelleralphabet

\(\Gamma=\Sigma\cup\Pi\) (unser Kelleralphabet besteht also aus Elementen des Terminal- und des Nonterminalalphabets.

Zustände

Die Regel \(A\rightarrow\omega_1,…,\omega_n\) wird zu \(\delta(s_0,\epsilon,A):=\{(s_0,\epsilon)\}\). In unserem Fall sind das:

\(\delta(s_0,\epsilon,S):=\{(s_0,\epsilon)\}\)

\(\delta(s_0,\epsilon,S):=\{(s_0,SS)\}\)

\(\delta(s_0,\epsilon,S):=\{(s_0,[S])\}\)

\(\delta(s_0,\epsilon,S):=\{(s_0,(S))\}\)

Dazu brauchen wir auch noch Regeln für die Terminalzeichen (\(\delta(s_0,a,a):=\{(s_0,\epsilon)\}\)), so dass nur mit der Verarbeitung weitergemacht werden soll wenn das oberste Zeichen im Keller mit dem eingelesenen Zeichen übereinstimmt:

\(\delta(s_0,(,():=\{(s_0,\epsilon)\}\)

\(\delta(s_0,),)):=\{(s_0,\epsilon)\}\)

\(\delta(s_0,[,[):=\{(s_0,\epsilon)\}\)

\(\delta(s_0,],]):=\{(s_0,\epsilon)\}\)

Zusätzlich müssen wir das Kellerstartsymbol durch \(S\) ersetzen um loszulegen:

\(\delta(s_0,\epsilon,\$):=\{(s_0,S)\}\)

Achtung: wir haben hier ein Beispiel gezeigt, dass die Sprache mittels leerem Keller akzeptiert und nicht mittels Endzuständen! Das ist der Automat, der raus kommt (\(Z\) ist das Kellerendzeichen und \(\lambda\) ist unser leeres Wort \(\epsilon\), bzw. beliebiges Zeichen):

 

Download: Dyck-Sprache JFLAP Datei

Der Automat ist nichtdeterministisch angelegt, d.h. es existieren mehrere Berechnungspfade für eine Eingabe. Das werdet Ihr sehen wenn Ihr den Automaten laufen lasst. Es geht uns beim Nichtdeterminismus ja nur darum mindestens einen Berechnungspfad zu haben, der durchläuft. Dass andere evtl. scheitern ist uns in diesem Sinne egal. Die Regeln beim Automaten bedeuten folgendes:

(1) \(\lambda,Z,S\Rightarrow\)Wenn auf dem Eingabeband ein Zeichen \(\lambda\) (ein Zeichen nicht aus dem Alphabet) steht und das oberste Zeichen im Keller das Kelleranfangszeichen \(Z\) ist, ersetze es im Keller mit \(S\).

(2) \(\lambda,S,\lambda\Rightarrow\)Wenn auf dem Eingabeband ein Zeichen \(\lambda\) und im Keller ein \(S\) steht, so ersetze \(S\) im Keller mit \(\lambda\). Damit ist der Keller leer, es ist unsere „Endbedingung“. Nicht vergessen: der Keller wird erst dann geleert (auf \(\lambda\) gesetzt) wenn wir fertig mit dem Einlesen (es steht \(\lambda\) auf dem Eingabeband) und am Ende im Keller nur ein \(S\) stand, d.h. dass wir einen korrekten Berechnungspfad hatten und damit das Wort richtig abgeleitet wurde.

(3) \(\lambda,Z,S\Rightarrow\)Wenn auf dem Eingabeband ein Zeichen \(\lambda\) steht und das oberste Zeichen im Keller das Zeichen \(S\) ist, ersetze es im Keller mit \((S)\).

(4) \(\lambda,Z,S\Rightarrow\)Wenn auf dem Eingabeband ein Zeichen \(\lambda\) steht und das oberste Zeichen im Keller das Zeichen \(S\) ist, ersetze es im Keller mit \([S]\).

(5) \(\lambda,Z,S\Rightarrow\)Wenn auf dem Eingabeband ein Zeichen \(\lambda\) steht und das oberste Zeichen im Keller das Zeichen \(S\) ist, ersetze es im Keller mit \(SS\).

Spätestens jetzt habt Ihr ein Fragezeichen über dem Kopf. Oder Ihr nickt. Oder ihr fragt euch, warum ich um den heißen Brei herumrede. Habt Ihr gemerkt? Welche Regel von den letzten drei wird nun angewendet wenn auf dem Eingabeband das Zeichen eines leeren Wortes \(\lambda\) steht und das oberste Zeichen im Keller das Zeichen \(S\) ist? Wird da nun ein \((S), [S]\) oder \(SS\) draus? Tja, das genau ist der Nichtdeterminismus. Es kann alles sein. Und wenn wir den falschen Pfad wählen, können wir evtl. nie aus der Berechnung raus. Und wisst Ihr was? Es ist uns egal! Hauptsache es existiert ein Pfad, das reicht uns.

Nun kommen die wichtigsten Regeln:

(6) \(],],\lambda\Rightarrow\)Wenn auf dem Eingabeband das Zeichen \(]\) steht und das oberste Zeichen im Keller ebenfalls \(]\) ist, ersetze es im Keller mit \(\lambda\).

(7) \([,[,\lambda\Rightarrow\)Wenn auf dem Eingabeband das Zeichen \([\) steht und das oberste Zeichen im Keller ebenfalls \([\) ist, ersetze es im Keller mit \(\lambda\).

(8) \((,(,\lambda\Rightarrow\)Wenn auf dem Eingabeband das Zeichen \((\) steht und das oberste Zeichen im Keller ebenfalls \((\) ist, ersetze es im Keller mit \(\lambda\).

(9) \(),),\lambda\Rightarrow\)Wenn auf dem Eingabeband das Zeichen \()\) steht und das oberste Zeichen im Keller ebenfalls \()\) ist, ersetze es im Keller mit \(\lambda\).

Wir leeren mit diesen Regeln also unseren Keller. Es fällt euch wahrscheinlich schwer, zu verstehen was der Automat tut. Ich würde sagen, wir probieren ihn an einem kleinen Beispiel aus.

Funktionsweise: Wenn wir z.B. den Automaten mit der Eingabe \(„()“\) laufen lassen, so passiert folgendes:

Ich habe nicht alle Pfade aufgemalt, sondern nur einen korrekten Pfad bis zum Ende durchgezeichnet. Die mit \(…\) beschrifteten Pfade führen zu einer weiteren Berechnung (die evtl. auch in einem Ergebnis münden kann). Nach Anwendung der Regel \(4\) und \(2\) in der zweiten Ableitung gibt es für die Symbolkombination \(\lambda,(\) oder \(\lambda,\lambda\) keinen weiteren Übergang und wir haben einen undefinierten Automatenzustand.

Bei den zwei weiteren Pfaden geht es jedoch weiter. Um den Keller zu leeren müssen wir als erstes Kellerzeichen und erstes Bandzeichen eines der vier Klammern haben. Da wir immernoch bei \((\) als Eingabe sind, müssen wir es schaffen auf das Hilfsband eine öffnende Klammer \((\) zu bekommen, was durch Anwendung der Regel 3 gut funktioniert. Bei den anderen drei Pfaden führt einer wieder in die Sackgasse, da wir keinen Folgezustand für die Symbolkombination \(\lambda,[\) oder \((,[\) haben und die beiden anderen zu weiteren Berechnungspfaden.

Der für uns spannende Pfad wird durch Regel 3 verfolgt: es wird mit Regel 8 anschließend ein Zeichen auf dem Hilfsband gelöscht und wir lesen das nächste Zeichen, unsere schließende Klammer \()\) oder \(\lambda\) ein und suchen für die Symbolkombination \(\lambda,S\) oder \(), S\) die nächsten, passenden Regeln. Es kommen wieder vier Berechnungspfade in Frage, die wir nun nicht weiter verfolgen. Sonst wäre die Grafik riesig geworden.

Mit Anwendung der Regel 2 ersetzen wir das \(S\) im Keller durch \(\lambda\) und können nun die einzig passende Regel \(9\) für die Symbolkombination \(),)\) anwenden um das nächste Zeichen (wir haben keins mehr) auf dem Eingabeband einzulesen und \()\) im Keller zu löschen.

Für Die Symbolkombination \(\lambda,S\) haben wir wieder vier mögliche Regeln, die passen könnten. Aber nur Regel 2 führt uns zu einem leeren Keller beim erreichen des Eingabeendes. Und damit haben wir einen Pfad erfolgreich gefunden.

Wir haben hier zeigen können, dass wir mit nur einem Zustand auskommen. Daher sollte der wichtige Satz

Für jeden Automaten, der eine Sprache \(L\) mittels Endzustand akzeptiert, existiert ein Automat, der die \(L\) mittels leerem Keller akzeptiert und umgekehrt (Vorsicht: das gilt nicht für deterministische Kellerautomaten!).

nicht vergessen werden!

Wie konstruieren wir denn aus einem Automaten mit mehreren Zuständen einen mit nur einem Zustand? Ganz einfach:

1. Aus dem Automaten mit mehreren Zuständen wird eine kontextfreie Grammatik erzeugt (nach Rechenberg ist das immer möglich, hat aber keine praktische Bedeutung und wird deshalb in der Literatur ausgelassen. Tatsächlich habe ich in vier Büchern, die ich zur Hand habe den Weg anhand eines konkreten Beispiels nicht gefunden. Wer etwas findet, bitte Info an mich. Mit dem JFLOP könnt Ihr einen Automaten in eine Grammatik wandeln, evtl. schreibe ich das Verfahren einfach nochmal hierhin)

2. Aus der kontextfreien Grammatik wird mit dem oben angegebenen Verfahren ein Automat mit nur einem Zustand erstellt

That’s it.

Zusammengefasst: Wir können also zu einer kontextfreien Sprache eine kontextfreie Grammatik \(G\) angeben. Diese Sprache erkennt auch ein Kellerautomat mittels leerem Keller. Auch ein Automat mit Endzustand tut dies. Wir können sogar einen Automaten angeben, der nur mit einem Zustand auskommt, da die Mächtigkeit des Automaten nur von seinem Keller kommt.

Noch eine Kleinigkeit, die hier von Bedeutung ist: was ist unter einem normalisierten Automaten zu verstehen ist? Dieser spielt bei bei der Konvertierung von Automat zu Grammatik eine große Rolle (hier ist ein gutes Dokument der Fakultät für Informatik der Uni Illionois, die etwas mehr Details dazu hat, als ich hier wiedergebe):

1. Es gibt nur einen akzeptierenden Endzustand

Das tun wir, indem wir einen neuen Endzustand einführen und einen \(\epsilon\)-Übergang von den anderen Zuständen dorthin zeichnen

2. Vor der Akzeptanz wird der Keller geleert

Das kann man tun, indem man vor dem Endzustand in einen Zustand geht und alles bis zum Kellerendzeichen (\(\\)$) aus dem Keller schmeißt.

3. Beim Übergang wird entweder ein Zeichen aus dem Keller entnommen oder eines hineingelegt, aber nicht beides

Hier gibt es zwei Fälle: a) Übergänge, die ein Element aus dem Keller nehmen und ein neues hinein legen und b) Übergänge, die nichts tun. Beide können wir mit neuen Zuständen und Übergängen simulieren. Fall a) handeln wir ab, indem wir zwei neue Zustände einführen: einer entnimmt das Zeichen, geht in einen temporären (neuen) Folgezustand über, dann wird ein Zeichen hineingelegt und der eig. Folgezustand eingenommen. Fall b) behandelt wir noch einfacher: wir basteln uns zwei neue Übergänge. Einer nimmt das Zeichen, geht in den temporären (neuen) Folgezustand und der nächste legt es wieder zurück. Fertig.

Das war jetzt alles wahrscheinlich bisschen viel und verwirrend. Vielleicht hilft eine kurze Übersicht des Beweisverfahrens?

Beweisverfahren

Sprache \(L\Rightarrow\)

Kellerautomat \(A\Rightarrow\)

normalisierter Kellerautomat \(\overline{A}\Rightarrow\)

Grammatik \(G\Rightarrow\)

Sprache \(L\) und Kellerautomat mit nur einem Zustand \(A^{‚}\Rightarrow\).

Damit schließt sich der Kreis. Wir zeigen der Vollständigkeit halber im letzten Schritt auch noch, dass wir mit dem oben genannten Verfahren aus der erzeugten Grammatik einen Automaten (nach dem oben gezeigten Verfahren) ableiten können, der nur einen einzigen Zustand hat und das Wort mittels leerem Keller akzeptiert.

Wollen wir den ganzen Spaß noch einmal an der Sprache vom Anfang des Beitrags durchspielen:

Beispiel: \(LC_2=\{a^n b^n\mid n\in\mathbb{N}\}\)

Sprache zu Kellerautomat

Dieser Automat erkennt die Sprache mit einem leeren Keller.

Kellerautomat zu normalisiertem Kellerautomat

Dieser Automat erkennt die Sprache mittels Endzustand. So sieht er aus:

Wie wir sehen, haben wir einfach nur einen neuen Endzustand eingeführt. Der folgende Automat erkennt also das Wort in einem Endzustand und hat auch noch einen leeren Keller. Also optimale Bedingungen. Damit ist er soweit normalisiert (bis auf den Punkt mit den Überführungsbedingungen: die tun immer noch zwei Schritte gleichzeitig (Push und Pop). Da sie uns aber bei der Grammatik nicht stören, war hier etwas faul, sorry!).

Normalisierter Kellerautomat mit Endzustand zu Grammatik

Nun wandeln wir die Zustandsübergänge des Automaten in die Regeln für die Grammatik um. Wir kümmern uns zunächst um alle Regeln, die etwas aus dem Keller entnehmen (nicht vergessen, im Bild ist \(\lambda\) unser \(\epsilon\))

1. \(\delta(s_i,a,A)=\{(s_j,\epsilon)\}\Rightarrow s_{i}As_{j}\rightarrow a\)

\(\delta(s_0,b,A)=\{(s_1,\epsilon)\}\Rightarrow s_{0}As_{1}\rightarrow b\)

\(\delta(s_1,b,A)=\{(s_1,\epsilon)\}\Rightarrow s_{1}As_{1}\rightarrow b\)

\(\delta(s_1,\epsilon,Z)=\{(q_2,\epsilon)\}\Rightarrow s_{1}Zq_{2}\rightarrow\epsilon\)

Jetzt wird es haariger. Was machen wir mit den verbliebenen Regeln? Problem hierbei: wir nehmen was aus dem Keller und legen gleichzeitig was drauf. Erinnert Ihr euch an die Kriterien für die Normalisierung? Nunja, eine haben wir hier nicht erfüllt: Nr. 3. Aber das macht erstmal nichts, wir generieren einfach ein paar Regeln mehr nach folgendem Muster:

2. \(\delta(s_i,a,A)=\{(s_j,BC)\}\Rightarrow s_{j}As_{x}\rightarrow a(s_{j}Bs_{y})(s_{y}Cs_{x})\), wobei \(s_x\) und \(s_y\) alle Zustände im Automaten sind. Wir müssen also alle Zustandskombinationen abgrasen, was uns zur folgenden, langen Liste an Regeln führt:

Regel \(a,A;AA\)

\(\delta(s_0,A,s_0)=\{(s_0,AA)\}\Rightarrow s_{0}As_{0}\rightarrow{a(s_{0}As_{0})(s_{0}As_{0})}\)

\(\delta(s_0,A,s_0)=\{(s_0,AA)\}\Rightarrow s_{0}As_{1}\rightarrow{a(s_{0}As_{0})(s_{0}As_{1})}\)

\(\delta(s_0,A,s_0)=\{(s_0,AA)\}\Rightarrow s_{0}Aq_{2}\rightarrow{a(s_{0}As_{0})(s_{0}Aq_{2})}\)

\(\delta(s_0,A,s_0)=\{(s_0,AA)\}\Rightarrow s_{0}As_{0}\rightarrow{a(s_{0}As_{1})(s_{1}As_{0})}\)

\(\delta(s_0,A,s_0)=\{(s_0,AA)\}\Rightarrow s_{0}As_{1}\rightarrow{a(s_{0}As_{1})(s_{1}As_{1})}\)

\(\delta(s_0,A,s_0)=\{(s_0,AA)\}\Rightarrow s_{0}Aq_{2}\rightarrow{a(s_{0}As_{1})(s_{1}Aq_{2})}\)

\(\delta(s_0,A,s_0)=\{(s_0,AA)\}\Rightarrow s_{0}As_{0}\rightarrow{a(s_{0}Aq_{2})(q_{2}As_{0})}\)

\(\delta(s_0,A,s_0)=\{(s_0,AA)\}\Rightarrow s_{0}As_{1}\rightarrow{a(s_{0}Aq_{2})(q_{2}As_{1})}\)

\(\delta(s_0,A,s_0)=\{(s_0,AA)\}\Rightarrow s_{0}Aq_{2}\rightarrow{a(s_{0}Aq_{2})(q_{2}Aq_{2})}\)

Regel \(a,Z;AZ\)

\(\delta(s_0,Z,s_0)=\{(s_0,AZ)\}\Rightarrow s_{0}Zs_{0}\rightarrow{a(s_{0}As_{0})(s_{0}Zs_{0})}\)

\(\delta(s_0,Z,s_0)=\{(s_0,AZ)\}\Rightarrow s_{0}Zs_{1}\rightarrow{a(s_{0}As_{0})(s_{0}Zs_{1})}\)

\(\delta(s_0,Z,s_0)=\{(s_0,AZ)\}\Rightarrow s_{0}Zq_{2}\rightarrow{a(s_{0}As_{0})(s_{0}Zq_{2})}\)

\(\delta(s_0,Z,s_0)=\{(s_0,AZ)\}\Rightarrow s_{0}Zs_{0}\rightarrow{a(s_{0}As_{1})(s_{1}Zs_{0})}\)

\(\delta(s_0,Z,s_0)=\{(s_0,AZ)\}\Rightarrow s_{0}Zs_{1}\rightarrow{a(s_{0}As_{1})(s_{1}Zs_{1})}\)

\(\delta(s_0,Z,s_0)=\{(s_0,AZ)\}\Rightarrow s_{0}Zq_{2}\rightarrow{a(s_{0}As_{1})(s_{1}Zq_{2})}\)

\(\delta(s_0,Z,s_0)=\{(s_0,AZ)\}\Rightarrow s_{0}Zs_{0}\rightarrow{a(s_{0}Aq_{2})(q_{2}Zs_{0})}\)

\(\delta(s_0,Z,s_0)=\{(s_0,AZ)\}\Rightarrow s_{0}Zs_{1}\rightarrow{a(s_{0}Aq_{2})(q_{2}Zs_{1})}\)

\(\delta(s_0,Z,s_0)=\{(s_0,AZ)\}\Rightarrow s_{0}Zq_{2}\rightarrow{a(s_{0}Aq_{2})(q_{2}Zq_{2})}\)

3. Nun werden die Zustandskombinationen noch umbenannt in \(A,B,C, …\), unnötiges gestrichen (man kann sich einen Abhängigkeitsgraphen malen um unnötige Zustände besser zu identifizieren, wie z.B. in diesem Beitrag gezeigt) und der Startzustand \(S\rightarrow s_0Zq2\) hinzugefügt. Am Ende haben wir dann die folgenden Regeln für unsere Grammatik:

\(S\rightarrow aCA\)

\(C\rightarrow b\mid aCG\)

\(G\rightarrow b\)

\(A\rightarrow\epsilon\)

 Wir könnten hier sogar noch \(G\) oder \(C\) streichen und kommen auf

\(S\rightarrow aCA\)

\(C\rightarrow b\mid aCC\)

\(A\rightarrow\epsilon\)

Grammatik zu Kellerautomat mit nur einem Zustand

Da wir nun unsere Grammatik haben, können wir nach dem Verfahren von oben (erstes Beispiel bei Lernziel 4) uns einen schönen Automaten mit nur einem Zustand basteln, der die Worte unserer Sprache mit leerem Keller akzeptiert. Das sind die Zustandsübergänge, die wir aus der Grammatik ableiten können:

\(S\rightarrow aCA\)

\(\delta(s_0,\epsilon,A)=\{(s_0,aCA)\}\)

\(C\rightarrow b\mid aCC\)

\(\delta(s_0,\epsilon,C)=\{(s_0,b)\}\)

\(\delta(s_0,\epsilon,C)=\{(s_0,aCC)\}\)

\(A\rightarrow\epsilon\)

\(\delta(s_0,\epsilon,A)=\{(s_0,\epsilon)\}\)

Fehlen uns noch die Regeln für die Terminale und die Ersetzung des Kellerzeichens durch erste Ableitung \(S\) wenn wir fertig sind:

\(\delta(s_0,a,a)=\{(s_0,\epsilon)\}\)

\(\delta(s_0,b,b)=\{(s_0,\epsilon)\}\)

\(\delta(s_0,\epsilon,Z)=\{(s_0,S)\}\)

Nachdem wir alles zusammengefügt haben, kommt der folgende Automat heraus:

Grammatik zu Sprache

Letzter Schritt nochmal aus der Grammatik die ableitbare Sprache zu basteln:

\(LC_2=\{a^n b^n\mid n\in\mathbb{N}\}\)

Damit ist der Kreis geschlossen und wir sind da, wo wir angefangen haben. Und ich hoffe, dass ich mich nirgendwo vertippt habe… 😉

Antwort zum Lernziel: zu jedem nichtdeterministischen Kellerautomat, der eine Sprache mittels Endzustand erkennt kann man einen nichtdeterministischen Kellerautomaten angeben, der dieselbe Sprache mittels leerem Keller (ohne Endzustand) erkennen kann. Und das sogar mit nur einem einzigen Zustand. Das liegt daran, dass die Ausdrucksstärke nur vom Keller und nicht von den Zuständen des Automaten kommt.

Dieser Automat kann weiter normiert werden, so dass man beim Erreichen des Endzustands einen leeren Keller hat und die Überführungsfunktionen entweder etwas auf den Stack legen oder nur etwas wegnehmen. Dazu werden die Überführungsfunktionen, die diese Kriterien nicht erfüllen durch neue, temporäre Zustände und neue Regeln ersetzt.

Der normierte Automat lässt sich dann einfacher in eine kontextfreie Grammatik umwandeln, das die gleiche Sprache erzeugt wie der normierte Automat. Dazu werden die Überführungsrelationen des Automaten in Ableitungsregeln für die Grammatik umgewandelt, ein Abhängigkeitsgraph gezeichnet und unnötige Zustände und Relationen mit seiner Hilfe gestrichen, so dass sich die Menge der Ableitungen auf ein Minimum verkürzt.

Am Ende hat man eine minimale Grammatik, aus der man zum einen die Sprache ableiten, als auch wieder einen Automaten mit nur einem einzigen Zustand erzeugen kann, der die von der Grammatik erzeugte Sprache mittels leerem Keller akzeptiert.