Einzelschrittfunktion

Manchmal ist es notwendig den Funktionswert einer Funktion zu berechnen. Die Funktion ist uns durch ein Flussdiagramm mit initialer Registerbelegung (Eingabewerte) gegeben und wir möchten nun das Ergebnis berechnen. Dazu ein Beispiel anhand eines Flussdiagramms aus dem Skript.

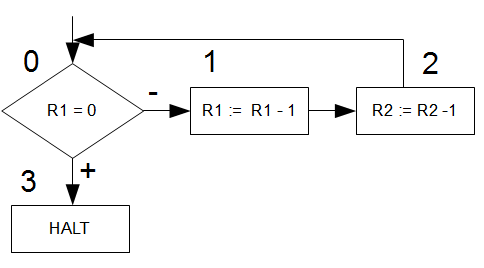
Beispiel (das – in Block 1 und 2 ist mangels mathematischer Zeichen in Open Office Draw als arithmetische Differenz zu deuten):

Wir möchten z.B. nun $f_M(2,1)$ berechnen (okay, das Beispiel ist etwas blöd, da das Ergebnis in $R_0$ immer 0 ist, aber sei es drum). Wir verwenden hierzu die Einzelschritt-Notation für die Berechnung um die Schritte nachvollziehbar zu machen. Diese haben die Form: $ES^n(Block,(R_0, R_1, R_2, 0, …)$. Merke: in $R_0$ steht das Ergebnis. Block gibt an in welchem Block wir uns befinden, $n$ gibt uns die noch durchzuführenden Schritte an und in $R_1, …, R_n$ ist die derzeitige Registerbelegung aller weiteren verwendeten Register (ohne das Ergebnisregister). Die restlichen Register sind mit 0 gefüllt und werden mit $0,…$ angedeutet.

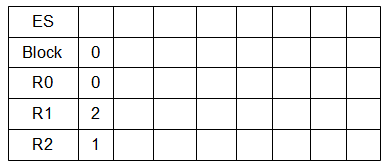
Wir stellen also eine kleine Tabelle auf und füllen diese Schritt für Schritt. Da wir unser $n$ aus $ES^n$ noch nicht wissen, wird es als letztes gefüllt. Für die Berechnung von $f_M(2,1)$ starten wir also bei Block 0 mit der Belegung $R_0 = 0$ (unser Ergebnis, initial mit 0 belegt), $R_1 = 2$ (unser Register Nr. 1) und $R_2 = 1$ (unser Register Nr. 2). Das führt uns zur Tabelle:

Damit haben wir schon unseren ersten Schritt mit $ES^n(0(,0,2,1,…))$. $n$ können wir, wie gesagt, noch nicht füllen, da wir die Schritte noch nicht abzählen können. Nun schauen wir nach, was in Block 1 passiert. Hier wird das Register $R_1$ auf 0 getestet. Ist das wahr, so landen wir bei Block 3 (HALT). Ist es nicht wahr, bei Block 1. In unserem Fall landen wir bei Block 1 und füllen die zweite Spalte unserer Tabelle. Achtung: die einzutragende Registerbelegung ist die beim Eintritt gültige Belegung der Register, d.h. der Berechnungsschritt aus dem Block fand noch nicht statt. Wir füllen der Abkürzung halber noch schnell alle anderen Spalten:

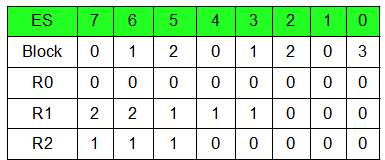
Wir erreichen nach 7 Schritten den Block 3 (HALT) und beenden die Berechnung. Damit haben wir nun unser $f_M(2,1) = 0$ (Ergebnis steht ja am Ende Register $R_0$ wie wir wissen). Und auch unser $n$ aus $ES^n$ ist mittlerweile gefunden. Die Gesamtrechnung für den Lösungsweg sieht dann so aus:

$ES^7(0,(0,2,1,…)$
$=ES^6(1,(0,2,1,…) $
$=ES^5(2,(0,1,1,…)$
$=ES^4(0,(0,1,0,…)$
$=ES^3(1,(0,1,0,…)$
$=ES^2(2,(0,0,0,…)$
$=ES^1(0,(0,0,0,…)$
$=(3,(0,0,0,…)$
und somit
$f_M(2,1) = 0$.

Schrittzahlfunktion

Die Schrittzahlfunktion $SZ(q,d)$ bedeutet nichts anderes, als die Anzahl der Schritte dir man ausgehend von der Konfiguration $d$ bei der Anfangsmarke $q$ benötigt um zu einer Endkonfiguration zu kommen. Nehmen wir einfach das beispiel von oben: Für $(q,d) = (0,(0,2,1))$ wäre $SZ(0,(0,2,1)) = 7$.

Gesamtschrittfunktion

Die Gesamtschrittfunktion $GS(q,d)$ ist die Endkonfiguration bei der Eingabe von $(q,d)$. Führen wir das beispiel von oben fort, so landen wir bei der Eingabe von $(0,(0,2,1))$ am Ende bei $(3,(0,0,0))$. Damit ist $GS(0,(0,2,1) = (3,(0,0,0))$.

Übergangsrelationen

Das wird uns noch häufiger begegnen, deswegen werde ich das mal hier noch in aller Deutlichkeit aufschreiben. Die Übergangsrelation ist auch definiert als:

$k_1 \vdash^t k_2\Longleftrightarrow{ES^t(k_1) = k_2}$

Hier bedeutet es, dass das Flussdiagramm mit der Eingabekonfiguration $k_1$ gestartet wird und in $t$ Schritten in die Endkonfiguration $k_2$ übergeht. Um das Beispiel von oben zu bemühen wäre das:

$(0,(0,2,1)) \vdash^7 (3,(0,0,0)) \Longleftrightarrow{ES^7(0,(0,2,1) =(3,(0,0,0))}$

That’s it. Ggf. füge ich noch die anderen Definitionen der Übergangsrelation bei Gelegenheit ein. Die sollten aber ziemlich selbsterklärend sein wenn man das Beispiel sieht.

Wie immer gilt: bei Fehlern bitte melden!

Update: im Hinblick auf die Lernziele zu Kurseinheit 1, habe ich diesen Eintrag etwas überarbeitet um ihn im neuen Beitrag verwenden zu können.

Wichtig vorab: lasst euch nicht von den mathematischen Definitionen erschrecken. Sie werden nach der Einführung der formalen Definition noch einmal informell (und hoffentlich verständlich) erläutert. Auch wenn euch die Definitionen unnötig erscheinen, ist es in der Mathematik üblich etwas unmissverständlich auszudrücken. Die formale Definition ist daher leider notwendig und durchaus hilfreich bei den Prüfungen und den Einsendeaufgaben. Aber mal Butter bei die Fische:

Wir unterscheiden die Maschinen in normale Registermaschinen und allgemeine Registermaschinen. Der Unterschied zwischen den beiden ist, dass die allgemeinen Registermaschinen zusätzliche, komplexe Funktionen anbieten. Diese müssen jedoch durch normale Registermaschinen ausgedrückt werden können. Als Beispiel dient der (komplexe) Vergleich von zwei Registern, welcher durch eine normale Registermaschine ausgedrückt werden kann.

Die Registermaschine verfügt über Register $$R_0, R_1, R2, …$$ zum Speichern natürlicher Zahlen. Eine Belegung der Register wird mit einer Funktion $$d: \mathbb{N} \rightarrow \mathbb{N}$$ realisiert. $$d(i)$$ ist der Inhalt des Registers $$R_i$$. Die Datenmenge der Registermaschine ist damit $$D := \mathbb{N}^{\mathbb{N}} = \{d \mid d : \mathbb{N} \rightarrow \mathbb{N}\}$$. Die Funktion $$d(i)$$ lässt sich auch als konkrete Belegung der Register mit $$(d(0), d(1), d(2), …)$$ darstellen, z.B. „(3, 1, 5, …)“. Man verwendet hier so viele Funktionswerte, d.h. belegte Register wie notwendig. Alle anderen Register sind mit 0 belegt. Zusätzlich wird mit der Ausgabecodierung $$AC: D \rightarrow \mathbb{N}$$ mit $$AC(d) := d(0)$$ definiert, dass das Ergebnis stets im Register $$R_0$$ stehen soll.

Die einzigen Operationen, die eine normale Registermaschine kann ist

addiere 1 in $$R_i$$ ($$R_i := R_i + 1$$)
subtrahiere 1 in $$R_i$$ ($$R_i := R_i \dot{-} 1$$), arithemtische Differenz ($$a – b := ( a – b$$ falls $$a \geq b$$, 0 sonst), z.B. 5 $$\dot{-}$$ 7 = 0, aber 7$$\dot{-}$$ 5 = 2
teste ob in $$R_i$$ eine 0 steht. ($$R_i = 0$$)

Alle anderen Operationen finden sich in einer allgemeinen Registermaschine wieder und werden, wie erwähnt, durch die drei Operationen der normalen Registermaschine ausgedrückt. Nun definieren wir die beiden Arten der Registermaschine formal und erklären die Definition. Anschließend folgt ein Beispiel für eine Funktion, deren Berechenbarkeit wir durch eine allgemeine Registermaschine beweisen. Ihre komplexen Funktionen bilden wir dann mit einer normalen Registermaschine nach.

Definition Registermaschine

Eine k-stellige ($$k \in \mathbb{N} $$) Registermachine ist wie folgt definiert: $$M = (F, \mathbb{N}^k, \mathbb{N}, EC^{(k)}, AC) $$. Stelligkeit bedeutet einfach nur die Anzahl der verwendeten Register. Ist die Stelligkeit mit $$k = 0$$ angegeben, gilt $$D:=\{\}$$, d.h. die Registerbelegung ist $$(0,0,…)$$.

$$D := \mathbb{N}^{\mathbb{N}} = \{d \mid d : \mathbb{N} \rightarrow \mathbb{N}\}$$ als die Menge der Registerbelegungen.
$$F$$: ist ein Flussdiagramm (siehe Beispiel im „berechenbare Zahlenfunktion“)
$$EC^{(k)}: \mathbb{N}^k \rightarrow D$$ mit $$EC^{(k)}(x_1,…,x_k)=(0,x_1,…,x_k,0,…)$$: Eingabecodierung mit $$k$$ Stellen und der Menge $$D$$ als Datenmenge auf der operiert wird.
Beispiel: $$EC^{(3)}(3,5,1)=(0,3,5,1,0,…)$$
Wir belegen die Register $$1-3$$ der Registermaschine also mit $$3,5,1$$, wobei das erste (Ausgaberegister) und alle anderen Register mit $$0$$ belegt werden.
$$AC : D \rightarrow \mathbb{N}$$: als Ausgabecodierung mit $$AC(a_0,a_1,…):=a_0$$
D.h. im 1. Register der Registermaschine $$R_0$$ steht die Ausgabe.
Die Funktionen und Tests wie oben beschrieben.

Damit haben wir die Registermaschine auch schon definiert.

Verallgemeinerte Registermaschine

Die verallgemeinerte Registermaschine ist ebenfalls k-stellig und hat die gleiche Definition $$M = (F, \mathbb{N}^k, \mathbb{N}, EC^{(k)}, AC) $$. Der einzige Unterschied ist, dass statt den drei rudimentären Funktionen (Addition, Subtraktion/arithmetische Differenz, Test auf 0) zusätzlich noch weitere, komplexe Funktionen und Tests definiert sind. Wir lassen nun folgende Operationen zusätzlich zu:

$$R_n:=g(R_{i1},…,R_{im})$$: das bedeutet nichts anderes, als dass wir ein Register auf ein Wert setzen können, der durch eine Funktion $$g$$ errechnet worden ist, wobei die Eingabeparameter für $$g$$ aus den Registern $$R_{i1},…,R_{im}$$ stammen.
Beisipel: $$g(x,y)=x+y$$ mit Registermaschinenbelegung $$EC^3(4,1,2)=(0,4,1,2,…)$$
Die Zuweisung $$R_0=g(R_1,R_3)$$ ist damit gültig und das Ergebnis ist $$R_0=6$$
$$R_i\neq R_j$$: wir können nicht mehr nur auf $$0$$ testen, sondern können schauen ob der Registerinhalt von $$R_i$$ ungleich dem Registerinhalt von $$R_j$$ ist.

Im Beitrag über berechenbare Zahlenfunktionen kommt ein Beweis einer dieser komplexen Funktionen der allgemeinen Registermaschine vor: der Multiplikation. Wer noch etwas Nachhilfe bei der vollständigen Induktion bei den Maschinen braucht, dem könnte der Beitrag vielleicht helfen.

Wie immer gilt: bei Fehlern bitte melden!