Theoretische Informatik – Seite 10 – Informatik an der Fernuni

1. Mai 201325. November 2025

TIB: Separations- und Hierarchiesätze (Lernziele KE2, Update 2)

Update 4: MathJax wollte nicht so, wie ich oder einige Leser des Blogs. Nun sollten alle Symbole wieder angezeigt werden.

Update 3: Ein kleiner Exkurs zum Thema $P-NP$ wurde hinzugefügt.

Update 2: Zwei Fehler in der Berechnung im Lernziel 3 sind nun gefixt.

Update: Antworten zu Lernzielen hinzugefügt. Soweit möglich.

Lernziel 1

Verstehen des Verfahrens von Separations- und Hierarchiesätzen

(Großer Dank an Barbara, Oliver, Björn und Lothar aus der NG für die Tipps zu diesem Thema).

Zunächst: was sind Hierarchiesätze und wofür werden sie gebraucht? Der Satz aus der Wikipedia ist hier durchaus hilfreich:

Für die gebildeten Klassen möchte man möglichst beweisen, dass durch zusätzlich bereitgestellte Ressourcen tatsächlich mehr Probleme gelöst werden können. Diese Beweise bezeichnet man als Hierarchiesätze (auch Separationssätze genannt), da sie auf den Klassen der jeweiligen Ressource eine Hierarchie induzieren. Es gibt also Klassen, die in eine echte Teilmengenbeziehung gesetzt werden können. Wenn man solche echten Teilmengenbeziehungen ermittelt hat, lassen sich auch Aussagen darüber treffen, wie groß die Erhöhung einer Ressource sein muss, um damit eine größere Zahl von Problemen berechnen zu können.

…

Die Hierarchiesätze bilden letztlich das Fundament für die Separierung von Komplexitätsklassen. Sie bilden einige der frühesten Ergebnisse der Komplexitätstheorie.

…

D.h. wir haben hier die Möglichkeit Komplixitätsklassen von einander trennen zu können (wenn bestimmte Vorbedingungen erfüllt sind), so dass eine echte Inklusion erfüllt ist.

Bevor wir hier weitermachen, wiederholen wir noch einmal ein paar Kleinigkeiten aus den vorhergehenden Beiträgen zum Thema Sprache:

Eine Sprache $L(M)$ ist entscheidbar wenn die charakteristische Funktion

$\chi_L(\omega)=\begin{cases}1&\text{ falls }\omega\in{L}\\0&\text{ falls }\omega\notin{L}\end{cases}$

berechenbar ist. Es gibt noch die Definition mit „…hält für jede Eingabe.„, was natürlich auch korrekt ist.

Wir können diese Maschine so modifizieren, dass sie eine $1$$ ausgibt bevor sie im akzeptierenden Zustand hält oder in einem nicht-akzeptierenden Zustand hält und eine $0$ vorher ausgibt. Wie wir bald erfahren werden, ist das Wortproblem für $Typ-1$-Sprachen entscheidbar.

Beispiel: $L=\{a^n\mid n>10\}$. Wir können für jede Eingabe $x$ entscheiden ob $x$ den Einschränkungen genügt oder nicht.

Eine Sprache $L(M)$ ist aufzählbar wenn die charakteristische Funktion

${\chi_L}^{‚}(\omega)=\begin{cases}1&\text{ falls }\omega\in{L}\\\perp&\text{ falls }\omega\notin{L}\end{cases}$

berechenbar ist. Auch hier greife ich etwas vor: das Wortproblem für $Typ-0$-Sprachen ist nur semi-entscheidbar.

Beispiel: Halteproblem$L=\{i\#x\mid M_i\text{ haelt auf }x\}$ ist rekursiv aufzählbar. Hier besteht das Wort unserer Sprache aus $i\#x$, wobei $i$ die Codierung einer $TM$ ist und $x$ die Eingabe dazu. Da wir nicht entscheiden können, ob die Maschine $M_i$ bei der Eingabe von $x$ nicht hält, ist auch unsere daraus erstellte Sprache nur rekursiv aufzählbar.

Nun haben wir uns noch einmal klar gemacht, was eine Sprache ist und wann man sie als entscheidbar/rekursiv aufzählbar klassifizieren kann. Jetzt können wir über Komplexitätsklassen reden.

Beweis: Unterschiedlichkeit der Komplexitätsklassen

(Danke an Lothar für die geduldige Erklärung der Vorbedingungen)

Wie beweisen wir die Unterschiedlichkeit von Komplexitätsklassen? Dass z.B. $ZEIT(n)\subsetneqq ZEIT(n^2)$ ist? Mittels Diagonalisierung und universellen Maschinen. Bei dem Diagonalisierungsbeweis wird ein ähnliches Verfahren verwendet wie beim Selbstanwendbarkeitsproblem (spezielles Halteproblem, wir erinnern uns?): die Diagonalisierung erfolgt nicht über alle rekursiven Mengen, sondern über die Mengen in $ZEIT(f)$. Benötigt wird hierzu:

1. eine universelle, $f$-zeitbeschränkte Maschine (diese wird verwendet um zu prüfen, ob sich eine Menge in einer bestimmten Zeitschranke befindet)

2. ein Komplexitätsklasse mit Zeitschranke $g$

Der Beweis beim Zeitseparationssatz ($ZEIT(g)\nsubseteqq ZEIT(f)$) besteht im Grunde darin eine Menge $D$ zu konstruieren, die zwar in $ZEIT(g)$ liegt, aber nicht in $ZEIT(f)$. Das erfolgt als Diagonalbeweis indem man durch einen Widerspruch zunächst zeigt, dass die Menge $D\notin{ZEIT(f)}$ ist, was durch unsere universelle Maschine mit Laufzeit $f(n)\cdot log\text{ }f(n)$ entschieden wird.

Fazit: wir simulieren also eine Maschine, die die Sprache aus der Menge $ZEIT(g)$ (also eine Sprache, die in Laufzeit $O(g)$ entschieden wird) auf einer universellen Maschine entscheidet, die durch $f$ beschränkt ist. Wenn wir über die Beschränkung, die uns $f$ auferlegt laufen, so ist die Sprache nicht in $ZEIT(f)$.

Die schnellste Simulation einer $k$-Band Maschine durch eine universelle $2$-Band Maschine hat die Laufzeit $O(f(n)\cdot log\text{ }f(n))$, was klar ist: wir müssen zunächst die Maschine selbst simulieren (Faktor $f(n)$) und dann die $k$ Bänder auf 2 Bänder verkleinern (Faktor $log f(n)$). Würden wir nur ein Arbeitsband verwenden, so wäre der Aufwand nicht mehr $log\text{ }f(n)$, sondern $f(n)^2$ (siehe KE1).

Aus diesem Grund fordern wir auch, dass $g\notin O(f(n)\cdot log\text{ }f(n))$ ist damit wir die Sprache mit der Schranke $g$ auf unserer Maschine entscheiden können. Wäre $g\in O(f(n)\cdot log\text{ }f(n))$, so könnten wir nicht prüfen ob die Sprache akzeptiert wird, da unsere universelle Maschine für die Prüfung zu langsam ist, denn die hat genau die Laufzeit, wo auch $g$ drin wäre. Die universelle Maschine hätte also nicht genug Zeit die zu simulierende Maschine zu simulieren um die Akzeptanz der Sprache zu prüfen. Uah, was für ein Satz!

Anschließend erfolgt der Nachweis, dass $D\in{ZEIT(f)}$ indem wir eine Maschine angeben, die durch $f$ beschränkt ist und dennoch $D$ entscheiden kann und die Unterschiedlichkeit der zwei Komplexitätsklassen ist bewiesen.

Der Beweis für den Zerhierarchiesatz ($ZEIT(f)\subsetneq ZEIT(g)$) erfolgt genauso, nur wird vorausgesetzt, dass $f$ mindestens das gleiche Wachstum, wie $g$ hat: $f\in{O(g)}$.

Antwort zum Lernziel: Zeithierarchie- und separationssätze dienen dazu Komplexitätsklassen von einander zu trennen. Im Endeffekt geht es um Separierung und der Bildung von Hierarchien bei den Ressourcen Band und Zeit.

Was ist also unser Zeithierarchie- oder separationssatz? Schreiben wir sie uns zunächst einmal auf (ich empfehle euch, dass Ihr das auf dem Papier auch macht):

Lernziel 2

Voraussetzung für Separations- und Hierarchiesätze benennen und begründen

Zeitseparationssatz:

Sei $f, g: \mathbb{N}\rightarrow\mathbb{N}$, $g$ zeitkonstruierbar, $n\in O(g)$, $g\notin O(f(n)\cdot\text{ }log f(n))$.

Dann ist $ZEIT(g)\nsubseteqq ZEIT(f)$

Damit $ZEIT(g)$ keine Teilmenge von $ZEIT(f)$ ist, müssen einige Voraussetzungen erfüllt sein. Diese sind:

1. Wir haben ein $g$, dass zeitkonstruierbar ist (die maximale Schrittzahlfunktion der $TM$ von $g$ hat als obere Schranke das Wachstum von $g$ für alle Eingaben, siehe unten),

2. ein $n\in O(g)$, $n$ bedeutet hier, dass $g$ mindestens linear wächst (könnten wir weglassen, da es bereits beim Lesen der Eingabe auf der universellen Maschine erreicht wird)

3. ein $g$, dass sich nicht in $O(f(n)\cdot log\text{ }f(n))$ befindet. D.h. $g$ hat als obere Schranke nicht $O(f(n)\cdot log\text{ }f(n))$ (der Grund ist, dass sich die durch $f$ beschränkte, zu simulierende Maschine mindestens in $O(f(n)\cdot\text{ }log f(n))$ simulieren lässt. Wäre $g$ noch in der oben angegebenen Schranke, könnten wir nicht entscheiden ob die Sprache aus $ZEIT(g)$ sich in $ZEIT(f)$ befindet).

Wir separieren also die Komplexitätsklassen der beiden Funktionen von einander wenn die oben genannten Voraussetzungen erfüllt sind.

Zeithierarchiesatz:

Sei $g: \mathbb{N}\rightarrow\mathbb{N}$ zeitkonstruierbar, $n\in O(g)$, $f: \mathbb{N}\rightarrow\mathbb{N}, f\in O(g), g\notin O(f(n)\cdot{log\text{ }f(n)})$.

Dann ist $ZEIT(f)\subsetneqq ZEIT(g)$

Damit $ZEIT(f)$ eine echte Teilmenge von $ZEIT(g)$ ist, müssen auch hier einige Voraussetzungen gelten. Nehmen wir sie auch hier auseinander:

1. Wir haben auch hier ein $g$, dass zeitkonstruierbar ist,

2. ein $n\in O(g)$, $n$ bedeutet hier, dass $g$ mindestens linear wächst

3. ein $f$, dass ${}\in O(g)$ ist ($g$ wächst damit mindestens so schnell wie $f$), während sich das

4. $g$ nicht in $O(f(n)\cdot log\text{ }f(n))$ befindet ($g$ wächst schneller als $O(f(n)\cdot log\text{ }f(n))$).

Wir wir sehen können, sind das fast die selben Vorbedingungen wie für den Separationssatz. Damit $ZEIT(f)$ jedoch eine Teilmenge sein kann, muss sich $f$ zusätzlich in $O(g)$ befinden. Erst dann gilt: $ZEIT(f)\subsetneqq ZEIT(g)$. Was haben wir hier am Ende getan? Wir haben eine Hierarchie zwischen den beiden Komplexitätsklassen geschaffen, so dass $ZEIT(f)$ eine echte Teilmenge von $ZEIT(g)$ darstellt.

Weil es wo schön war: noch einmal den ganzen Spaß mit dem Bandhierarchie- und dem Bandseparationssatz:

Bandseparationssatz:

Sei $g: \mathbb{N}\rightarrow\mathbb{N}$, $g$ bandkonstruierbar, $log\in O(g)$, $f:\mathbb{N}\rightarrow\mathbb{N}$.

Dann gilt $BAND(g)\subseteq BAND(f)\Leftrightarrow g\in O(f)$

Damit $BAND(g)$ eine Teilmenge (im Gegensatz zu „keine Teilmenge“ beim Zeitseparationssatz) von $BAND(f)$ ist und $f$ als obere Schranke für das bandbedarfswachstum $g$ gilt, müssen folgende Voraussetzungen erfüllt sein:

1. ein bandkonstruierbares $g$ ($\tilde{s}_M$, d.h. der maximale Speicher- bzw. Bandbedarf der Maschine muss in der Komplexitätsklasse von $O(g)$ liegen),

2. $log\in O(g)$, $g$ wächst also mindestens logarithmisch und wir haben ein

3. ein $f$ mit Definitions- und Bildmenge aus $\mathbb{N}$.

4. Dazu ist $f$ eine obere Schranke für $g$

Auch hier haben wir eine Separation des Bandbedarfs, genauer der Komplexitätsklassen des Bandbedarfs von Funktionen $f$ und $g$ und können zudem auch sagen, dass die obere Schranke für das Bandbedarfswachstum von $g$ eben $O(f)$ ist. Ist ja auch klar, denn es gilt (wenn die Voraussetzungen erfüllt sind) $BAND(g)\subseteq BAND(g)$.

Kommen wir nun zum Bandhierarchiesatz:

Bandhierarchiesatz:

Sei $log\in O(g)$, $g$ bandkonstruierbar, $f\in O(g)$, $g\notin O(f)$.

Dann gilt $BAND(f)\subsetneqq{BAND(g)}$

Damit $BAND(f)$ also eine echte Teilmenge von $BAND(g)$ darstellt, kämpfen wir mit den folgenden Voraussetzungen: notwendig sind

1. ein bandkonstruierbares $g$ (siehe oben),

2. $log\in O(g)$, $g$ wächst also mindestens logarithmisch, wir haben ein

3. ein $f\in O(g)$, d.h. $f$ hast $g$ als obere Schranke und

4. ein $g\notin O(f)$, also ist $f$ keine obere Schranke für $g$

Mit dem Hierarchiesatz haben wir es auch hier geschafft eine Hierarchie auf den Komplexitätsklassen des Bandbedarfs herzustellen. Während wir beim Separationssatz durchaus gleiche Mengen haben könnten (z.B. ist $\{1,2,3\}$ eine Teilmenge von $\{1,2,3\}$) , haben wir das beim Hierarchiesatz nicht ($\{1,2\}$ eine echte Teilmenge von $\{1,2,3\}$). Bitte macht euch nochmal den Unterschied klar.

Antwort zum Lernziel: Die Voraussetzungen für Separation und Hierarchie begründen sich in der $TM$, auf denen die Funktion simuliert wird.

Für die Separation von $g$ und $f$ muss $g$ zeitkonstruierbar sein (Schrittzahlfunktion der $TM$ muss noch innerhalb der Schranke der Funktion liegen), min. lineares Wachstum haben (da die Eingabe von der $TM$ gelesen werden muss und wir z.B. beim Lesen von $n$ durch die Unärnotation schon $n$ Schritte verbrauchen) und sich nicht in $O(f(n)\cdot log f(n))$ (da wir die $f$-beschränkte Maschine simulieren müssen und die Simulation bereits in $O(f(n)\cdot log\text{ }f(n))$ erfolgt) befinden.

Bei der Hierarchie haben wir ähnliche Vorbedingungen, müssen aber zusätzlich sicherstellen, dass die zu untersuchende Funktion $f$ innerhalb der Schranke für $g$ liegt.

Die Selbsttestaufgabe aus dem Skript ist hier anschaulich, ich möchte mich daher auch in dem Beitrag daran halten.

Lernziel 3

Anwendung der Sätze zum Beweis von Separationen und echten Inklusionen

Beispiel

$f(n)=\begin{cases}n, &\mbox{falls }n\mbox{ gerade}\\n^3, &\mbox{sonst}\end{cases}$

$g(n) = n^2$

Beide Funktionen sind zeitkonstruierbar. Behauptung:

(1) $ZEIT(f)\subseteq ZEIT(g)$

Wir benötigen hier also unseren Zeitseparationssatz:

Sei $f, g: \mathbb{N}\rightarrow\mathbb{N}$, $g$ zeitkonstruierbar, $n\in O(g)$, $g\notin O(f(n)\cdot\text{ }log f(n))$. Dann ist $ZEIT(g)\nsubseteqq ZEIT(f)$

Fangen wir mit Behauptung (1) an: $ZEIT(f)\subseteq ZEIT(g)$

Wir setzen $g=n$ oder $g=n^3$ je nach Fall. Und $f=n^2$

(im Satz wird ja nicht $ZEIT(f)\nsubseteqq ZEIT(g)$, sondern $ZEIT(g)\nsubseteqq ZEIT(f)$ geprüft).

Vorbedingungen, die wir erfüllen müssen für den Zeitseparationssatz sind also:

1. $g$ muss zeitkonstruierbar sein: check!

2. $g$ muss mindestens lineares Wachstum haben: check!

3. die obere Schranke für $g$ ist nicht $O(f(n)\cdot log\text{ }f(n))$: auch wenn man das sieht, prüfen wir das doch mal:

Fall 1

Wenn $n$ gerade, muss gelten: $n\notin O(n^2\cdot log(n^2))$. Gilt es? Nein!

Fall 2

Ist $n$ ungerade, muss gelten: $n^3\notin O(n^2\cdot log(n^2))$. Gilt dies? Ja! Die Voraussetzung ist hier also erfüllt.

Da bei einem ungeraden $n$ die Voraussetzungen für die Separation gegeben sind, ist $ZEIT(f)\nsubseteqq ZEIT(g)$. Hätten wir nur ein $n$ statt $n^3$, so wäre die Voraussetzung nicht gegeben. Aber so gilt der Separationssatz für ungerade $n$ und damit ist Behauptung (1) falsch.

Antwort zum Lernziel: Siehe oben. Auf zwei gegebene Funktionen $f$ und $g$ kann man die Zeit- und Bandhierarchiesätze anwenden (wenn die Voraussetzungen zutreffen) und so eine Hierarchie oder eine Separierung der Komplexitätsklassen vornehmen.

Lernziel 4

Definition von band- und zeitkonstruierbaren Funktionen

Was ist eine band- bzw. zeitkonstruierbare Funktion? Das Wachstum so einer Funktion entspricht dem Bandbedarf, bzw. der Schrittzahlfunktion eine real existierenden Turingmaschine. Was man sich merken sollte ist, dass zwar alle zeitkonstruierbaren Funktionen bandkonstruierbar sind. Andersherum geht es aber nicht. Das folgt aufgrund des Zusammenhangs zwischen Band und Zeit. Hangeln wir uns an der Definition entlang:

$f: \mathbb{N} \rightarrow\mathbb{N}$ heißt bandkonstruierbar, falls es eine TM $M$ gibt, so dass $\forall n. f_M(0^n) = 0^{f(n)}, \tilde{s}_M\in O(f)$

Was muss vorliegen damit die Funktion bandkonstruierbar ist? $\tilde{s}_M$, d.h. der maximale Speicher- bzw. Bandbedarf der Maschine muss in der Komplexitätsklasse von $O(f)$ liegen.

$f: \mathbb{N} \rightarrow\mathbb{N}$ heißt zeitkonstruierbar, falls es eine TM $M$ gibt, so dass $\forall n. f_M(0^n) = 0^{f(n)}, \tilde{t}_M\in O(f)$

Hier ist es ähnlich. Nochmal zur Erinnerung: $\tilde{t}_M$ ist die maximale Anzahl der Schritte, die die TM $M$ benötigt um bei der Eingabe eines Wertes die Endkonfiguration zu erreichen und $0^n$ ist die Unärnotation von $n$ (z.B. $5 = 00000$).

Nicht vergessen: $t_M \neq \tilde{t}_M$. Ersteres bezeichnet nämlich nur die Anzahl der Schritte bis zur Endkonfiguration bei einer bestimmten Angabe, letzteres die maximale Anzahl der Schritte bei allen Eingaben ($\tilde{t}_M := max\{t_M(x)|x\in \Sigma^n\}$).

Was müssen wir also tun um zu zeigen, dass eine Funktion $f$ zeitkonstruierbar ist? Die Aufgabe im Skript zeigt es relativ anschaulich, dem will ich mich also auch nicht verschließen.

Beispiel: zeigen, dass $f(n) = \lfloor n \cdot \sqrt{n} \rfloor$ zeitkonstruierbar ist.

Wir schauen in die Definition und merken, dass wir eine TM angeben müssen, deren Schrittzahlfunktion für alle Eingaben von $n$ innerhalb der Schranke $O(\lfloor n \cdot \sqrt{n} \rfloor)$ liegt. In dem Beispiel wird auch mit Dualzahlen gerechnet anstatt mit der unären Notation von $n$. Also nicht davon abschrecken lassen, d.h. $d(n)$ ist die Dualnotation von $n$ (z.B. $d(5) = 101$). Lange Rede, kurzer Sinn: es müssen also folgende Voraussetzungen für die Zeitkonstruierbarkeit erfüllt sein:

1. $f_M(0^n) = 0^{f(n)}$, z.B. $f_M(0^5) = 0^{11}$ (die TM berechnet also die Funktion und gibt sie in unärer Notation aus) und

2. $\tilde{t}_M\in O(f)$, die Schrittzahlfunktion der TM liegt innerhalb der Schranke $O(f)$, d.h. $O(\lfloor n \cdot \sqrt{n} \rfloor)$

Nochmal zum selber nachrechnen: $f(\lfloor n \cdot \sqrt{n} \rfloor)$ mit $n = 5 = 0^5 \rightarrow f(5) = 11$, $f(0^5) = 0^{11}$. Die Schritte, die zu der korrekten Berechnung im Skript gemacht werden sind:

1. Berechnung von $a = d(n)$

2. Berechnung von $b= a*a*a$

3. Berechnung von $c=d(\lfloor\sqrt{d^ {-1}(b)}\rfloor)$

4. Ausgabe von $0^{d^{-1}(c)}$

Probieren wir das mal am Beispiel $n = 5$

1. $ a = d(5) = 101$

2. $b = 101 * 101 * 101 = 1111101$

3. $ c =d(\lfloor\sqrt{d^ {-1}(1111101)}\rfloor) = 1011$

4. Ausgabe von $0^{d^{-1}(1011)} = 0^{11} = 00000000000$

Sieht also gut aus. Damit haben wir eine funktionierende TM für die Funktion und müssen nur noch schauen ob die Schritte bis zur Endkonfiguration, d.h. bis zu unseren Ausgabe auch in der Schranke $O(f)$, d.h. $O(\lfloor n \cdot \sqrt{n} \rfloor)$ liegen:

1. hier brauchen wir $O(n)$ Schritte

2. für die Multiplikation reicht die Schulmethode, welche uns zu $O((log n)^2)$ bringt.

3. mit der Intervallschachtelung kommen wir hier mit $O((log n)^3)$ Schritten aus.

4. für den letzten Schritt, die unäre Ausgabe werden mehr Schritte benötigt als bei den drei Schritten davor: $O(\lfloor n \cdot \sqrt{n} \rfloor)$.

Damit dominiert dieser Schritt die Rechenzeit und wir haben gezeigt, dass $O(f(n)) = O(\lfloor n \cdot \sqrt{n} \rfloor)$ und damit zeitkonstruierbar ist.

Wenn wir das Beispiel nachvollziehen konnten, so ist auch klar geworden, dass z.B. die Funktionen $log n$ und $\lfloor\sqrt{n}\rfloor$ nicht zeitkonstruierbar sind, denn sie benötigen mehr Schritte zur Berechnung als $log n$ und $\lfloor\sqrt{n}\rfloor$ und passen daher nicht in die oberen Schranken, die wir für die Zeitkonstruierbarkeit benötigen.

Antwort zum Lernziel: Für eine Zeit- und Bandkonstruktion bei einer Funktion $f$ müssen wir zeigen, dass die maximale Schrittzahlfunktion $\tilde{t}_M$ und der maximale Speicherplatzbedarf $\tilde{s}_M$ innerhalb der Schranke $O(f)$ liegt. Ist uns das gelungen ist die Funktion $f$ zeit- bzw. bandkonstruierbar.

Lernziel 5

Beschreibung des Beweises von $ZEIT(n)\subsetneqq{ZEIT(n\cdot log\text{ }n)}$

Antwort zum Lernziel: Hier muss ich erstmal passen. Wer eine schöne Beschreibung der Beweisidee hat, bitte melden.

Lernziel 6

Beweis der Beziehungen zwischen den Klassen P, LOGSPACE, PSPACE

Um die Beziehungen zwischen P, LOGSPACE und PSPACE zu verstehen, müssen wir zunächst einmal wissen, was P, LOGSPACE und PSPACE ist. Fangen wir mit der Klasse P an:

$P:=\bigcup_{k\in\mathbb{N}} ZEIT(n^k)$

Was das? Die Klasse $P$ ist die unendliche Vereinigung der Zeitkomplexitätsklassen $ZEIT(f)$. In der Literatur wird sie auch Polynomialzeit genannt. Es bezeichnet die Klasse der effizient lösbaren Probleme. $P$ ist eine Teilmenge von $NP$, d.h. $P\subseteq NP$ (hier kommt auch das berühmte P-NP-Problem her), aber dazu später mehr. Dann haben wir noch:

$PSPACE:=\bigcup_{k\in\mathbb{N}} BAND(n^k)$

Und das ist eine unendliche Vereinigung der Bandkomplexitätsklassen $BAND(f)$. Letztendlich haben wir auch noch:

$LOGSPACE:=\bigcup_{k\in\mathbb{N}} BAND(log)$

$LOGSPACE$ gilt als die kleinste Bandkomplexitätsklasse.

Die Beziehung zwischen diesen ist wie folgt:

$LOGSPACE\subseteq P\subseteq PSPACE$

und

$LOGSPACE\subsetneqq PSPACE$.

Warum das so ist, wird klar wenn man sich die Definition der 4 Komplexitätsklassen anschaut und sich die Beziehungen vor Augen führt:

In $PSPACE$ sind alle Bandkomplexitätsklassen drin, die maximal einen polynomialen Bandbedarf haben. Dass $LOGSPACE$ eine echte Teilmenge davon ist (Unterschied zwischen Teilmenge und echte Teilmenge klar?), sollte einleuchten (logarithmischer Platzbedarf ist zwar ein Teil, aber sicher kleiner als polynomialer Platzbedarf. Daher auch echte Teilmenge und nicht nur Teilmenge). Damit haben wir schon einmal $LOGSPACE\subsetneqq PSPACE$ erklärt.

Durch den Satz aus Kurseinheit 1:

$(1)$ Sei $f:\mathbb{N}\rightarrow\mathbb{N}$. Dann gilt: $ZEIT(f)\subseteq BAND(f)$

$(1)$ Sei $log\in O(f)$. Dann ist $BAND(f)\subseteq \bigcup_{c\in\mathbb{N}} ZEIT(c^{f(n)})$

haben wir auch unsere Beziehung zwischen $LOGSPACE$, $PSPACE$ und $P$ hergestellt.

Um $(1)$ und $(2)$ nachzuvollziehen müssen wir uns nur noch einmal daran erinnern, dass der Platzbedarf nie größer sein kann als die die Anzahl der maximalen Schritte, die eine Maschine tun kann. Denn in jedem Schritt können wir nur ein Feld beschreiben. Wir beschränken so nicht nur die Maschine, sondern auch ihren Bandverbrauch.

Damit ist $LOGSPACE\subseteq{P}\subseteq PSPACE$.

Wo ist $LOGTIME$? Diese Klasse ist nicht sonderlich spannend, wenn auch vorhanden. In $LOGTIME$ liegt z.B. das Nachschauen in einer sortierten Liste. Wir schauen uns die nicht komplett an, sondern gucken nach einem Element, welches sich irgendwo befinden kann. Die binäre Suche ist ein prominenter Vertreter eines Algorithmus in der Komplexitätsklasse $LOGTIME$.

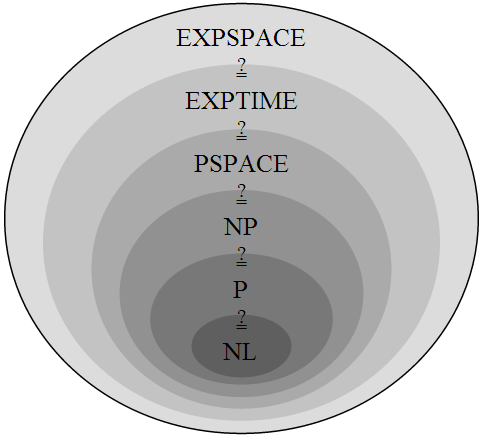
Der Vollständigkeit halber: die vollständige Beziehung zwischen den einzelnen Komplexitätsklassen ist (nichtdeterministische Problemklassen ausgelassen): $L\subseteq P\subseteq NP\subseteq PSPACE$.

Quelle: Wikipedia

Antwort zum Lernziel: die Beziehungen zwischen den Klassen erfolgen mittels den Hierarchieseätzen für Band und die folgende Teilmengen-Beziehung zwischen Zeit und Band gilt: $ZEIT(f)\subseteq BAND(f)$. Damit bilden wir eine Hierarchie zwischen $LOGSPACE$, $P$ und $PSCAPE$ hergestellt.

Wer noch ein paar Details zum Thema $P-NP$ haben möchte, der kann sich den folgenden Beitrag anschauen und sich schon ein klein wenig auf die nun folgenden Kurseinheiten zu diesem Thema einstimmen.

Wieder gilt: wer Fehler findet, bitte ASAP in die Kommentare oder per Mail damit falsches Zeug nicht zu lange online steht.

15. April 201325. November 2025

TIA: Berechenbarkeit auf anderen Mengen (Lernziele KE7, 1/2)

Update: auch diesen Beitrag habe ich auf die Lernziele gemünzt und ein paar Fehler behoben.

Bei dieser KE fühlt es sich leicht an wie ein kleiner Bruch. Es ist ein komplett neues Thema und so erschließt sich auf den ersten Seiten nicht unbedingt der Sinn dahinter. Zumindest mir nicht. Erst gegen Ende der Kurseinheit sieht man, wo die Reise hingegangen ist: zu der Berechenbarkeit der reellen Zahlen. Denn vorher haben wir nur die Berechenbarkeit von Wort- und Zahlenfunktionen betrachtet.

Ich werde daher immer ein Stück vorgreifen wenn ich denke, dass es dem Verständnis förderlich ist und mir nicht die Pointe für den Schluss aufheben.

Lernziel 1

Definition der Berechenbarkeitskonzepte, welche durch eien Nummerierung auf einer Menge $M$induziert werden: $\nu$-rekursiv, $\nu$-r.a, $(\nu,{\nu}^{‚})$-berechenbar

Wir erinnern uns noch an die Churchsche These? Wenn nicht, bitte nochmal nachlesen. Wird hier noch einmal wichtig werden. Im Grunde geht es hier wieder um die Verschlüsselung von Elementen aus abzählbaren Mengen (hier sei nochmal erwähnt: eine Menge ist abzählbar wenn sie die gleiche Mächtigkeit wie $\mathbb{N}$ hat) durch Zahlen oder Wörter, da wir Zahlen mit Register- und Wörter mit Turingmaschinen berechnen können.

Wir erinnern uns auch an unsere Standardnummerierung $\nu_\Sigma$ oder die Nummerierung der einstelligen berechenbaren Zahlenfunktionen $\varphi$. Diese sind total (überall definiert) und sogar bijektiv (bis auf $\varphi$). Nun führen wir ein weiteres Berechenbarkeitskonzept ein, dass nicht weit weg von dem ist, was wir schon haben. Nehmen wir die Definition also Stück für Stück auseinander.

Es seien $\nu: \subseteq \mathbb{N} \rightarrow M$ und $\nu: \subseteq \mathbb{N} \rightarrow M_1$ Nummerierungen.

Eine Menge $X \subseteq M$ heißt $\nu$–rekursiv, gdw. es eine berechenbare Funktion $g: \subseteq \mathbb{N} \rightarrow \mathbb{N}$ gibt mit:
$g(i)=\begin{cases}1&\text{falls } \nu(i) \in X \\0&\text{sonst }\end{cases}$
für alle $i \in Def(\nu)$.

Das ist das Äquivalent zu unserer Entscheidbarkeit/Rekursivität für Zahlen- und Wortfunktionen. Durch die Nummerierung $\nu$ nummerieren wir alle Elemente aus der Menge $M_1$ und die Funktion $g$ entscheidet für uns ob die gegebene Nummer eines Elements aus $M_1$ uns zu einem Element bringt, dass in der Menge $X$ liegt oder nicht.

Es geht uns also im Endeffekt nur darum die Elemente aus der Menge $X$ zu entscheiden.

Machen wir erst einmal weiter im Text. Anschließend folgt ein Beispiel um es etwas „greifbarer“ zu machen.

Eine Menge $X \subseteq M$ heißt $\nu$–rekursiv-aufzählbar, gdw. es eine berechenbare Funktion $g: \subseteq \mathbb{N} \rightarrow \mathbb{N}$ gibt mit:
$g(i)=\begin{cases}existiert&\text{falls } \nu(i) \in X \\div&\text{sonst }\end{cases}$
für alle $i \in Def(\nu)$.

Und hier haben wir das Äquivalent zu unserer Semi-Entscheidbarkeit/rekursiver Aufzählbarkeit.

Wir können zwar immer sagen, ob ein Element zu einer Menge $X$ gehört, haben aber bei der gegenteiligen Aussage ein Problem. Denn hier divergiert die Funktion, sie gibt uns also kein Ergebnis und kann unendlich laufen. Es ist also festgelegt, dass wir im positiven Fall (irgendwann) eine Antwort erhalten, im negativen Fall aber nicht. Prominente Beispiele für die Semi-Entscheidbarkeit sind – wie im verlinkten Beitrag erwähnt – das Halteproblem und der Busy Beaver.

Und nun die letzte Definition für diesen Abschnitt. Hier geht es nicht um eine Menge, sondern um eine Funktion:

Eine Funktion $f \subseteq M_1 \rightarrow M$ heißt $(\nu_1,\nu)$-berechenbar, gdw. es eine berechenbare Funktion $g: \subseteq \mathbb{N} \rightarrow \mathbb{N}$ gibt mit:

$f \circ \nu_1(i) = \nu \circ g(i)$ für alle $i$ mit $\nu_1(i) \in Def(f)$.

Wenn man es ausklammert, hat man vielleicht einen besseren Blick auf die Funktion: $f(\nu_1(i)) = \nu(g(i))$ für alle $i$ mit $\nu_1(i)\in Def(f)$. Okay, das hat nicht unbedingt super geklappt. Diese definition bedeutet, dass eine Menge $(\nu_1,\nu)$-berechenbar ist wenn es ein Verfahren gibt, dass uns zu jeder $\nu_1$-Nummer eines Elements der Definitionsmenge von $f$ eine $\nu$-Nummer der Bildmenge von $f$ berechnet.

Während also die Funktion $f$ auf ihren Mengen (zu einem Definitionswert aus $M_1$ gibt es durch die Funktion einen Funktionswert aus $M$) herumrechnet, kümmern wir uns mit der Funktion $g$ um die Umrechnung der „Nummerierungsnummern“ $\nu$ und $\nu_1$ der beiden Mengen $M_1$ und $M$.

Okay, das ist wahrscheinlich nicht sonderlich einleuchtend. Ich würde sagen, wir suchen uns ein nettes Beispiel.

Was wir zum Durchspielen der Definition brauchen sind

zwei Nummerierungen $\nu$ und $\nu_1$,
zwei Funktionen $f: \subseteq M_1 \rightarrow M$ (diese Funktion nimmt als Argument ein Element aus der Menge $M_1$ entgegen und gibt uns als Ergebnis ein Element aus der Menge $M$) und
$g: \subseteq \mathbb{N} \rightarrow \mathbb{N}$ (diese jedoch bekommt als Argument ein Element aus den natürlichen Zahlen $\mathbb{N}$ und gibt uns auch eins als Ergebnis zurück) und
unsere beiden Mengen $M$ und $M_1$.

Fangen wir einfach mal mit dem Beispiel an und belegen wir unsere Mengen, Funktionen und Nummerierungen mit konkreten Werten:

$M=\{2,4,6\}$: einfach willkürlich gewählt
$M_1=\{1,2,3\}$: ebenfalls willkürlich
$f \subseteq M_1 \rightarrow M: f(x) = 2x$. Willkürlich gewählt. Einzige Bedingung war, dass wir als Definition- und Bildwerte Elemente aus den Mengen $M_1$ und $M$ benutzen müssen. Also habe ich eine Funktion genommen, die Argumente aus $M_1$ auf Ergebnisse aus $M$ abbildet. Ihr könnt einfach mal andere Mengen wählen und die Funktion an diese anpassen. Das Ergebnis ist am Ende gleich.

Wenn wir die Funktion mit unseren Werten aus $M_1$ füttern, so bekommen wir: $f(1) = 2$, $f(2) = 4$ und $f(3) = 6$. Unsere Definitionsmenge $Def(f)$ ist also $\{1,2,3\}$ und entspricht wie gewünscht unserem $M_1$ (die Funktion $f$ ist hier sogar total, denn $Def(f) = M_1$, wie man sieht). Die Bildmenge, unsere Ergebniswerte der Funktion sind $Bild(f) = \{2,4,6\}$ und entsprechen also komplett unserer Menge $M$. Sie ist hier sogar surjektiv (auch rechtstotal genannt), denn $Bild(f) = M$ (jedes Element aus der Menge $M$ wird „getroffen“). Da wir auch noch injektiv (auch linkstotal genannt) sind, ist die Funktion bijektiv. Aber das nur nebenbei.

$g: \subseteq \mathbb{N} \rightarrow \mathbb{N}: g(x) = 2x$. Diese Funktion muss $f \circ \nu_1(i) = \nu \circ g(i)$ für alle $i$ mit $\nu_1(i) \in Def(f)$ erfüllen. Der Kreis $\circ$ ist ja bekanntlich einfach nur eine Komposition. Es muss also gelten: $f (\nu_1(i)) = \nu(g(i))$. Testen wir das doch gleich mit konkreten Werten. Aber vorher müssen wir unsere Nummerierungen wählen:
$\nu: \subseteq \mathbb{N} \rightarrow M$. Die Nummerierung von $M$ ist willkürlich gewählt, aber Hauptsache eindeutig und von $\nu_1$ verschieden. Wir nehmen einfach $-12$ für $\nu$, d.h. $\nu(14) = 2$, $\nu(16) = 4$ und $\nu(18) = 6$. Jetzt noch die Nummerierung der Elemente aus der Menge $M_1$.
$\nu_1: \subseteq \mathbb{N} \rightarrow M_1$. Hier nehmen wir $-6$ für $\nu_1$, d.h. $\nu_1(7) = 1$, $\nu(8) = 2$ und $\nu(9) = 3$. Damit ist auch die Menge $M_1$ nummeriert.

Jetzt können wir mal schauen, ob unsere Funktion $g$ die Bedingung $f \circ \nu_1(i) = \nu \circ g(i)$ erfüllt und probieren alle unsere Werte aus den Mengen $M$ und $M_1$ mal aus:

$\begin{array}{lcl}f(\nu_1(7))&=&f(1)\\{}&=&2\end{array}$

Und nun $g$:

$\begin{array}{lcl}\nu(g(7))&=&\nu(14)\\{}&=&2\end{array}$

Damit ist $f \circ \nu_1(7) = \nu \circ g(7)$ erfüllt. Probiert das doch mal mit den restlichen Werten $8$ und $9$ aus.

Mit dem Beispiel können wir auch die beiden Grafiken nachvollziehen, die im Skript drin stehen (ich habe beide Diagramme ein Stück weiter unten als Textform inkl. Beispiel beschrieben). Diese durch $f \circ \nu_1(i) = \nu \circ g(i)$ induzierte Beziehung bringt uns zu dem im Skript beschriebenen Ausdruck: Das Diagramm kommutiert.

Eine Funktion $f: \subseteq M_1 \rightarrow M$ ist $(\nu_1,\nu)$-berechenbar wenn es ein Verfahren gibt, welches zu jeder $\nu_1$-Nummer eines Elementes $x \in Def(f)$ eine $\nu$-Nummer von $f(x)$ berechnet.

Am obigen Beispiel angelehnt bedeutet es nichts weiter, dass unsere Funktion $f$ dann $(\nu_1,\nu)$-berechenbar ist wenn wir ein Verfahren zeigen können, dass zu jeder $\nu_1$-Nummer (also $,7,8,9$) eines $x \in Def(f)$ (also $1,2,3$) eine $\nu$-Nummer (also $14,16,18$) von $f(x)$ (also $2,4,6$) berechnet. Um es nochmal in Deutsch zu formulieren: wir müssen ein Verfahren angeben, welches uns zu einer gegebenen Zahl $v_1$-Nummer eine $v$-Nummer ausgibt.

Wählen wir z.B. als $\nu_1$-Nummer wieder die $7$, so müssen wir am Ende eine $14$ als $\nu$-Nummer herausbekommen: $\nu_1(7) = 1, f(1) = 2, \nu(2) = 14$. Anhand der Definitionen können wir so einfach ein Verfahren herleiten: $(2(i-6))+12 = 2i$. Damit bekommen wir zu jeder gegebenen $\nu_1$ eines $x \in Def(f)$ die zugehörige $\nu$-Nummer von $f(x)$. Das haben wir in dem Beispiel getan und gezeigt, dass unsere Funktion $f$ $(\nu_1,\nu)$-berechenbar ist.

Diese beiden Vierecke aus dem Skript sehen in Linie dargestellt wie folgt (inkl. Beispiel) aus:

Diagramm: $\mathbb{N}\rightarrow (g)\rightarrow \mathbb{N}\rightarrow (\nu)\rightarrow{M}\leftarrow (f)\leftarrow M_1\leftarrow (\nu_1)\leftarrow \mathbb{N}$

Beispiel: ${7}\rightarrow g(7)\rightarrow 14\rightarrow \nu(14)\rightarrow{2}\leftarrow f(1)\leftarrow 1\leftarrow \nu_1(7)\leftarrow 7$

Diagramm: $i\rightarrow (g)\rightarrow g(i)\rightarrow (\nu)\rightarrow{f(x)}\leftarrow (f)\leftarrow x\leftarrow (\nu_1)\leftarrow i$

Beispiel: $7\rightarrow g(7)\rightarrow 14\rightarrow \nu(14)\rightarrow{2}\leftarrow f(1)\leftarrow 1\leftarrow \nu_1(7)\leftarrow 7$

Beachtet hier bitte die Einschränkung aus dem Skript. Die Funktion $g$ arbeitet nur vernünftig für alle $i$ mit $\nu_1(i) \in Def(f)$. D.h. Das Ergebnis von $\nu_1(i)$ muss im Definitionsbereich unserer Funktion $f$ liegen. Dieser ist wie wir oben gesehen haben ja $Def(f) = M_1$ und $M_1=\{1,2,3\}$. Also muss das Ergebnis von $\nu_1(i)$ $1,2$ oder $3$ sein. Und das geht nur wenn $i \in \{7,8,9\}$ ist. Für alle anderen Werte für $i$ geht das natürlich nicht.

Antwort zum Lernziel: In den vergangenen Kurseinheiten haben wir uns um die Berechenbarkeit auf Zahlen- und Wortfunktionen gekümmert. In dieser Kurseinheit interessieren wir uns auf die Berechenbarkeitsmodelle auf beliebigen Mengen.

Um jedoch eine Berechenbarkeit auf diesen beliebigen Mengen zu induzieren, denn wir können mittels Register- und Turingmaschinen nur auf Zahlen oder Worten rechnen, brauchen wir Nummerierungen dieser Elemente und angepasste charakteristische Funktionen um unsere Definition für Rekursivität und rekursive Aufzählbarkeit auf diese Mengen zu übertragen.

Wir sind auch nicht nur auf eine einzige Nummerierung beschränkt, die uns Definitions- und Wertemenge nummeriert. Durch eine „Übersetzungsfunktionen“ können wir diese Nummerierungen ineinander „überführen“ und es uns so ermöglichen auf den unterschiedlichen Nummerierungen zweier Mengen rechnen zu können.

Lernziel 2

Nachweis der $\nu$-Rekursivität und $(\nu,{\nu}^{‚})$-Berechenbarkeit

Nun haben wie die $\nu$-Rekursivität, -rekursive-Aufzählbarkeit und $(\nu,{\nu}^{‚})$-Berechenbarkeit definiert, jetzt wollen wir auch etwas mit unserem Wissen anstellen.

Wollen wir doch mal versuchen das für zwei Beispiele aus dem Skript nachzuweisen.

Aufgabe 1: Nachweis der $(id_{\mathbb{N}},\nu)$-Berechenbarkeit einer Nummerierung $\nu: \subseteq \mathbb{N} \rightarrow M$.

Wir machen uns wieder klar, was wir hier zeigen müssen. Wir müssen zeigen, dass es ein Verfahren gibt, welches zu jeder $id_{\mathbb{N}}$-Nummer eines Elementes $x\in Def(\nu)$ eine $\nu$-Nummer von $\nu(x)$ berechnet. Etwas verwirrend, da die Definition noch ein $f$ verlangt, aber das $f$ ist in diesem Fall einfach nur die Nummerierung $\nu$.

Formal ausgedrückt:

$\nu \circ id_{\mathbb{N}}(i) = \nu \circ g(i)$ für alle $i$ mit $id_{\mathbb{N}}(i) \in Def(\nu)$

(nochmal zur Erinnerung $id_{\mathbb{N}}(k) = k$ für alle $k \in \mathbb{N}$, d.h. $id_{\mathbb{N}}(5) = 5$)

Wir suchen also ein $g$, dass die obige Gleichung erfüllt. Wenn Ihr die Komposition klammert sehr Ihr vielleicht auch schon, was für ein $g$ wir suchen:

$\nu (id_{\mathbb{N}}(i)) = \nu(g(i))$ für alle $i$ mit $id_{\mathbb{N}}(i) \in Def(\nu)$

Schon erkannt, was für ein $g$ wir suchen? Wir wählen als Beispiel wieder unsere Nummerierung $\nu$ von oben ($\nu(14) = 2, \nu(16) = 4,\nu(18) = 6$) und haben bei z.B. $i = 14$ folgende Gleichung (zunächst die linke Seite):

$\begin{array}{lcl}\nu (id_{\mathbb{N}}(14))&=&\nu(14)\\{}&=&2\end{array}$

Wir brauchen die Gleichung hier nur aufzulösen:

Wir müssen also $\nu(g(14)) = 2$ setzen. Was nummeriert mit der $2$ unser $\nu(?)=2$? Genau! Die $14$ wird durch $\nu$ mit der $2$ nummeriert (siehe oben): $\nu(14)=2$. Daher muss unser $g$ die $1$ auf die $14$ abbilden: $g(14)=14$ um die Gleichung zu erfüllen.

Aber jetzt habt Ihr sicher schon gemerkt, welches $g$ wir suchen.

Wir wählen $g=id_{\mathbb{N}}$ und rechnen die rechte Seite aus:

$\begin{array}{lcl}\nu (id_{\mathbb{N}}(14))&=&\nu(g(14))\\{}&=&\nu(14)\\{}&=&2\end{array}$

Passt! Damit ist unser $g$ richtig gefunden und es gilt:

$\nu (id_{\mathbb{N}}(i)) = \nu(id_{\mathbb{N}}(i))$

Die Nummerierung $\nu: \subseteq \mathbb{N} \rightarrow M$ ist damit $(id_{\mathbb{N}},\nu)$-berechenbar.

Aufgabe 2: zeigen, dass $\mathbb{Z}^+ := \{z\in\mathbb{Z} \mid z > 0\}$ $\nu_{\mathbb{Z}}$-rekursiv ist

Wir schauen nochmal nach oben auf die Definition der $\nu$-Rekursivität und sehen, dass wir eine Funktion $g$ angeben müssen, die für alle $i \in Def(\nu_{\mathbb{Z}})$ entscheidet ob das Element in $\mathbb{Z}^+$ liegt oder nicht.

Die Definition von $\nu_{\mathbb{Z}}$ ist: $\nu_{\mathbb{Z}} : \mathbb{N} \rightarrow \mathbb{Z}$, $\nu_{\mathbb{Z}}<i,j> := i-j$ $\forall i,j \in \mathbb{N}$.

Noch nicht so ganz klar? Kein Problem: schaut euch nochmal den Beitrag zur Cantorschen Tupelfunktion an, insbesondere die Inverse dazu.

Es gilt $\nu_\mathbb{Z}(500)=<27,4>$. Da $(i-j)>0$ gilt, gilt auch $i>j$. Wir geben nun unsere Funktion $g$ an:

$g<i,j>=\begin{cases}1&\text{falls } i > j \\0&\text{sonst }\end{cases}$

Die Funktion ist berechenbar (Ihr könnt ja mal eine Registermaschine angeben, die sie berechnet) und für alle $k \in \mathbb{N}$ gilt: $\nu_\mathbb{Z}(k) > 0\Longleftrightarrow g(k) = 1$. Die Menge ist also $\nu_\mathbb{Z}$-rekursiv.

Damit hätten wir schon fast die Hälfte abgehakt. Ich hoffe es war alles verständlich. Beitrag 2/2 folgt alsbald.

Und wieder ganz wichtig: wer Fehler findet, bitte sofort in die Kommentare damit niemand auf eine ungenaue Fährte gelockt wird.

Antwort zum Lernziel: Für den Nachweis der $\nu$-Rekursivität einer Menge $X$ muss man eine volle charakteristische Funktion $g$ angeben, die zu der Nummerierung $i$ angibt ob das nummerierte Element $\nu(i)$ in der Menge $X$ liegt oder nicht. Der Nachweis der rekursiven Aufzählbarkeit gelingt durch die „halbe“ charakteristische Funktion.

Für den Nachweis der Berechenbarkeit benötigen wir ein Verfahren, eine Funktion $g$, dass uns die unterschiedlichen Nummerierungen der beiden Mengen „umrechnet“, auf denen die Funktion $f$ eigentlich rechnet (ihre Definitions- und Wertemenge).

Noch ein paar wichtige Definitionen außerhalb der Lernziele, aber nicht weniger wichtig:

Eine weitere, naheliegende Eigenschaft der Nummerierungenen ist auch ihre Transitivität:

Sei $f\subseteq M_1\rightarrow M_2$ $(\nu_1,\nu_2)$-berechenbar und $g\subseteq M_2\rightarrow M_3$ $(\nu_2,\nu_3)$-berechenbar, so ist die Komposition von $g$ und $f$ $g\circ f$ $(\nu_1,\nu_3)$-berechenbar.

Konnte man sich schon fast denken. Braucht sicherlich nicht viele Erklärungen. Man kann direkt sehen, dass wir die Menge $M_2$ als Bindeglied zwischen $f$ und $g$ durch ihre Nummerierung $\nu_2$ haben.

Und nun noch etwas zur Notation:

Eine Notation der Menge $M$ ist eine ggf. partielle, surjektive Funktion $\nu:\subseteq\Sigma^{*}\rightarrow{M}$, wobei $\Sigma$ ein Alphabet ist.

Leuchtet ein. Wir können die Menge $M$ nicht nur nummerieren, wie wir das vorher getan haben und mit Registermaschinen berechnen, sondern wir können diese Menge auch mit Worten über einem Alphabet $\Sigma$ „nummerieren“. Nur nennt man das nicht mehr eine Nummerierung, sondern eine Notation!

Weiter geht es im folgenden Beitrag.

Kategorie: Theoretische Informatik

TIB: Separations- und Hierarchiesätze (Lernziele KE2, Update 2)

Lernziel 1

Lernziel 2

Lernziel 3

Lernziel 4

Lernziel 5

Lernziel 6

TIA: Berechenbarkeit auf anderen Mengen (Lernziele KE7, 1/2)

Lernziel 1

Lernziel 2

Buchempfehlung