Update: ich modelliere auch diesen Beitrag auf die Lernziele um. Evtl. kann es sein, dass der Beitrag nicht ganz fertig wird, so dass ein paar Antworten (noch) leer sind. Da ich ihn aber nicht speichern kann ohne ihn zu aktualisieren oder ihn offline nehmen müsste, habe ich keine andere Wahl als das zunächst so zu handhaben.
Update 6: Nachdem ich nun schon zwei Mails zum Thema \(\mu\)-Rekursion bekommen habe, möchte ich das hier noch einmal ausführen. Für die Details zum Thema Nullstellen möchte ich mich hier auch bei Oliver bedanken. Lernziel 5 also.
Update 5: mir ist was zur Standardnummerierung von \(\Sigma^{*}\) und \(P^{(1)}\) aufgefallen, dass ich hier passend unbedingt noch erwähnen musste.
Riesen Update: alle Lernziele habe ich nun überarbeitet und einige Ungenauigkeiten korrigiert. Der Beweis der nicht-berechenbaren Funktionen ist wohl auf das 10-fache des ursprünglichen Texts angewachsen. Irgendwie konnte ich mich mit dem alten Verweis auf das Diagonalrgument von Cantor für die Überabzählbarkeit der reellen Zahlen nicht anfreunden (beim ersten Erstellen hielt ich das noch für ausreichend) und habe den Skriptbeweis nun komplett auseinander genommen. Hoffentlich hilft es euch.
Kurseinheit 4 ist wieder ein Rundumschlag. Einige Dinge, die hier drin sind, hätten sich auch in Kurseinheit 2 wiederfinden müssen (LOOP, WHILE, Churchsche These und Zusammenhang zu \(\mu\)-rekursiven Funktionen. Taten sie aber nicht. Wäre wahrscheinlich einfach zu einfach gewesen. Ich würde daher vorschlagen, dass wir uns ausnahmsweise nicht thematisch, sondern anhand der Lernziele entlang hangeln.
Rekapitulation: Zahlen, Wörter
Nochmal als Wiederholung bevor wir loslegen.
Zahlenfunktionen: \(f:\subseteq \mathbb{N}^k \rightarrow \mathbb{N}\). D.h. Abbildung von ggf. mehrstelligen (unser \(k\)) Eingabewerten von natürlichen Zahlen auf einen einzigen Ausgabewert, eine einzige natürliche Zahl. Berechenbar mit Registermaschinen, nicht mit Turingmaschinen.
Konkretes Beispiel: \(f\subseteq\mathbb{N}^3\rightarrow\mathbb{N}\) mit \(f(x,y,z)=x+y-z\),
z.B. \(f(431,469,899)=1\)
Wortfunktionen: \(g:\subseteq \Sigma^{*k} \rightarrow \Sigma^{*}\). D.h. Abbildung von ggf. mehreren (wieder unser \(k\)) Eingabewerten von beliebig langen (unser \(*\)) Worten über einem Alphabet (unser \(\Sigma\)) auf einen einzigen Ausgabewert: ein einziges, beliebig langes Wort. \(\Sigma^{*}\) ist hier die Wortmenge über dem Alphabet \(\Sigma\). Berechenbar mit Turingmaschinen, nicht mit Registermaschinen.
Konkretes Beispiel: \(g:\subseteq \Sigma^{*2}\rightarrow \Sigma^{*}\) mit \(g(x,y)=xy\),
z.B. \(g(abbb,aaaa)=abbbaaaa\)
Wir können Zahlenfunktionen nicht auf Turingmaschinen und Wortfunktionen nicht auf Registermaschinen berechnen. Es gibt jedoch einen Weg: Erst wenn man Wörter in Zahlen codiert und Zahlen in Wörter (bijektive Abbildung zwischen zwei Mengen: Wörtern und Zahlen) kann man diese mit den entsprechend anderen Maschinen berechnen.
Ausgenutzt wird dabei, dass Registermaschinen und Turingmaschinen über Flussdiagramme definiert sind. Aber kümmern wir uns zunächst um die Standardnummerierung selbst.
Das ist die sogenannte Standardnummerierung (bijektive Abbildung zwischen den natürlichen Zahlen und einer Mengen). Definition kommt gleich. Es gibt jedoch einen wesentlichen Unterschied zu einer Nummerierung, der nicht verschwiegen werden darf.
Eine Nummerierung ist nicht bijektiv; Surjektivität reicht. Wir können in der Nummerierung dann jedem Wort mindestens eine Zahl zuordnen, aber wir haben keine eindeutige Umkehrabbildung, d.h. wenn wir dann zu einem Wort die zugehörige Zahl suchen, könnten wir diese mit etwas Pech auf mehrere Zahlen abbilden.
Achtung: während die Standardnummerierung von \(\Sigma^{*}\) durch \(\nu_\Sigma\) bijektiv ist, ist die Standardnummerierung der berechenbaren, einstelligen Funktionen \(P^{(1)}\) aus dem nächsten Beitrag das nicht! Warum, sage ich dann dort. Bitte behaltet das unbedingt im Hinterkopf.
Formal definiert ist eine Nummerierung also:
\(\nu:\subseteq\mathbb{N}\rightarrow{M}\)
Sie kann partiell sein und ist – wie gesagt – surjektiv. Damit hat zwar jedes Element aus der nummerierten Menge \(M\) eine Zahl aus \(\mathbb{N}\), aber nicht zu jeder Zahl aus \(\mathbb{N}\) gibt ein Element aus der Menge \(M\).
Und weil Marco mich in den Kommentaren zu KE5 auf die Idee gebracht hat, noch eine kleine Nebeninfo: Haben wir eine bijektive Abbildung zwischen zwei Mengen, gelten diese als gleichmächtig und die Eigenschaften der einen, gelten auch für die andere Menge. Bilden wir also die natürlichen Zahlen mittels einer bijektiven Funktion auf eine andere Menge ab, wie wir das mit der Standardnummerierung tun, so übernimmt diese Menge eine wunderbare Eigenschaft der natürlichen Zahlen \(\mathbb{N}\): sie ist dann ebenfalls abzählbar unendlich.
Lernziel 1
Angabe und Erläuterung der Definition einer Standardnummerierung von \(\Sigma^{*}\)
Nehmen wir als Beispiel ein Alphabet \(\Sigma\) mit \(n\) Symbolen, welches eine totale Ordnung hat (d.h. die \(n\) Symbole innerhalb des Alphabets sind – wie auch immer – eindeutig sortiert), so beinhaltet \(\Sigma^*\) alle Worte über dem Alphabet \(\Sigma\).
\(\nu_\Sigma(i)\) ist das \(i\)-te Wort aus dieser sortierten Liste. Die Sortierung nennt man Ordnungsfunktion. Das spannende an dieser Nummerierung ist, dass sie bijektiv ist. Wir haben also eine eindeutige Abbildung von einem Wort in eine Zahl und eine Inverse, die uns zu einer Zahl ein eindeutiges Wort liefert. Lasst uns die Definition mal formalisieren:
\(\Sigma\) ist ein Alphabet mit \(card(\Sigma) >= 1\).
\(a: \{1,…,n\} \rightarrow \Sigma\) die Ordnungsfunktion \(a\) mit \(a_i := a(i)\) und \(\Sigma = \{a_1, …, a_n\}\).
\(\sigma:\Sigma^* \rightarrow \mathbb{N}\) mit \(\sigma(\varepsilon):=0\) sowie
\(\sigma ({a_{i}}_{k} {a_{i}}_{k-1} … {a_{i}}_{1} {a_{i}}_{0}) := i_k n^k + i_{k-1} n^{k-1} + … i_1 n+i_0\) für alle \( k \in \mathbb{N}, i_0,…,i_k \in \{1,…,n\}\).
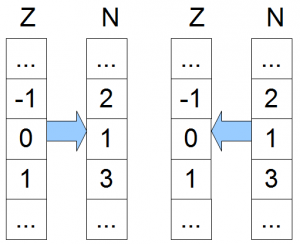
\(\nu_\Sigma : \mathbb{N} \rightarrow \Sigma^*\) ist unsere Inverse der Funktion \(\sigma\) und damit \(\nu_\Sigma := \sigma^{-1}\). Sie gibt uns zu einer gegebenen Zahl das entsprechende, eindeutige Wort zurück und wird Standardnummerierung von \(\Sigma^{*}\) genannt.
Keine Sorge, wir gehen das direkt an einem Beispiel durch.
Beispiel:
\(\Sigma = \{a,b\}\) mit \(card(\Sigma) = 2\) (Kardinalität, Mächtigkeit einer Menge). Ein Alphabet mit den Buchstaben \(a\) und \(b\), d.h. nur \(2\) Elementen und damit der Kardinalität \(2\).
Wir haben zwei Elemente \(a\) und \(b\) im Alphabet, also ist \(n = 2\) und wir haben \(a_1 = a(1) = a\) und \(a_2 = a(2) = b\): innerhalb der Wortmenge werden die Elemente wie im Skript nach Länge und dann lexikographisch geordnet. Die Menge \(\Sigma^*\) wäre dann
\(\Sigma^*=\{a,b,aa,ab,ba,bb,aaa,aab,aba,abb,baa,bab,bba,bbb,…\}\).
Wir haben nun jedem unserer zwei Elemente eine Ordnungszahl zugewiesen. Das ist unsere Ordnungsfunktion \(a\).
Der letzte Teil ist jetzt etwas ekelig, aber halb so wild. Erinnert mich irgendwie an SIMPLEX. Die Funktion \(\sigma\) macht nichts anderes, als zu einem bestimmten Wort die eindeutige Zahl anhand der definierten Ordnung zu bestimmen. Wir suchen z.B. die zugewiesene Zahl zu \(abb\). \(abb\) steht an 10. Stelle in der Reihenfolge und wir erwarten die \(10\) auch als Ergebnis.
\(n = 2\) (ist klar, die Kardinalität von \(\Sigma\), d.h. Anzahl der Elemente)
\(k = 2\) (das Wort \(abb\) besteht aus drei Elementen, wir zählen von \(0\) und haben damit \(k=2\))
\(i\) ist unsere Ordnungszahl. Da \(a\) zuerst kommt, ist \(a=1\) und da \(b\) an zweiter Stelle in unserer Ordnung kommt, ist \(b=2\). Hätten wir noch \(c\), so wäre \(c=3\) unserer festgelegten Ordnung nach.
\(\begin{array} {lcl}\sigma(abb)&=&1\cdot2^2 + 2\cdot2 + 2\\{}&=&4+4+2\\{}&=&10\end{array}\)
Und ja, \(abb\) steht an 10. Stelle in unserer Ordnung.
Man mache sich einfach klar, dass ein beliebiges Alphabet \(\Sigma\) definieren können, solange wir nur eine numerische Ordnung auf den Elementen des Alphabets definieren. Da wir aus den Elementen des Alphabets Worte bauen können, können wir auch aus den Ordnungszahlen, die den Elementen zugeordnet sind Kombinationen herstellen.
Die Ordnung ist ja nichts weiter als die Festlegung der Reihenfolge der verwendeten Elemente in unserem Alphabet. Damit rechnen wir statt mit den Buchstaben, nun mit ihren „Ordnungszahlen“. Und da auf den verwendeten, natürlichen Zahlen für unsere Reihenfolge auch eine natürliche Ordnung herrscht (\(1<2<3<4<…\)), können wir damit wunderbar rechnen.
Unser \(a\) im Alphabet repräsentiert unsere „Ordnungszahl“ \(1\) und \(b\) unsere „Ordnungszahl“ \(2\), welche wir dann oben in der Gleichung für \(\sigma(abb)\) verwendet haben und damit auf den Rechenweg \(1\) \(\cdot2^2 +\) \(2\) \(\cdot2^1 +\) \(2\) \(\cdot2^0\) kommen. Die grüne 1 ist daher die Ordnungszahl unseres \(a\) und die rote 2 die unseres \(b\).
Die Inverse zu \(\sigma(a)\) (\(a\) ist ein Wort) ist \(\sigma^{-1}=\nu_\Sigma(i)\) und gibt uns für eine Zahl \(i\) das dazugehörige Wort. Das 10. Wort wäre also \(\nu_\Sigma(10) = abb\).
Damit ist \(\nu_{\Sigma}\) eine Standardnummerierung von \(\Sigma^{*}\), also aller Worte über dem Alphabet \(\Sigma\).
Antwort zum Lernziel: die Standardnummerierung \(\nu_{\Sigma}\) der Worte über einem Alphabet \(\Sigma\) ist eine bijektive Abbildung zwischen den natürlichen Zahlen \(\mathbb{N}\) und den Worten aus \(\Sigma^{*}\). Die Bijektivität ist wichtig damit wir einer Zahl eindeutig ein Wort und einem Wort eindeutig eine Zahl zuweisen können.
Diese Zuweisung funktioniert aufgrund einer sog. Ordnungsfunktion \(a\) auf dem Alphabet \(\Sigma\), welches jedem Zeichen aus den Alphabet eine eindeutige Nummer (Ordnungszahl) aus den natürlichen Zahlen zuordnet. Durch die natürliche Ordnung auf den natürlichen Zahlen \(\mathbb{N}\) haben wir auch eine natürliche Ordnung auf den Elementen aus unserem Alphabet \(\Sigma\), die wir vorher nicht hatten.
Mit \(\sigma(a)\) bekommen wir somit zu einem Wort \(a\) die zugehörige Ordnungszahl \(i\) und mit \(\nu_{\Sigma}(i)\) zu einer Zahl \(i\) das zugehörige Wort aus den Worten über dem Alphabet \(\Sigma\): \(\Sigma^{*}\).
Lernziel 2
Formulierung und Erläuterung der Beziehung zwischen Zahlen- und Wortfunktionen
Zunächst noch einmal die Definition wann Wortfunktionen berechenbar sind:
Eine (ggf. partielle) Wortfunktion \(g : \subseteq (\Sigma^*)^k \rightarrow \Sigma^*\) ist genau dann berechenbar, wenn es eine Turing-Maschine \(T\) gibt, die die Funktion berechnet. Wenn also \(g =g_T\) gilt.
Das gleiche Spiel für Zahlenfunktionen.
Eine (ggf. partielle) Zahlenfunktion \(f : \subseteq \mathbb{N}^k \rightarrow \mathbb{N}\) ist genau dann berechenbar, wenn es eine Registermaschine \(M\) gibt, die die Funktion berechnet. Wenn also \(f = f_M\) gilt.
Kennen wir schon aus den alten Beiträgen. Registermaschinen für Zahlen- und Turingmaschinen für Wortfunktionen. Langweilig. But wait, there’s more! Im Zusammenhang mit der Standardnummerierung hatten wir das noch nicht. Denn wir können Wortfunktionen durchaus mit Registermaschinen und Zahlenfunktionen mit Turingmaschinen berechnen.
Man macht sich zunächst noch einmal folgenden Zusammenhang klar: Unsere (\(k\)-steligen) Wortfunktionen, welche die Turingmaschinen (Mehrbandmaschinen mit \(k\) Bändern) berechnen können, können auch auf Einbandmaschinen berechnet werden (Ihr erinnert euch: Spuren, Hilfssymbole, etc.?). Wir können uns also auf die Betrachtung der Einbandmaschinen für die Berechnung der Wortfunktionen beschränken.
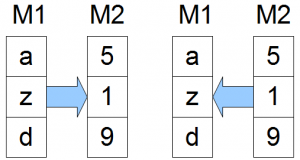
Und hier kommt die Standardnummerierung ins Spiel: wollen wir eine Wortfunktion auf einer Registermaschine berechnen, geht das zunächst nicht. Die Registermaschine rechnet ja mit Zahlen und nicht mit Worten. Und auch als Ausgabe bekommen wir eine Zahl und kein Wort. Aber hey! Wir können die Worte ja mit unserer Standardnummerierung eindeutig auf Zahlen und Zahlen eindeutig auf Worte abbilden. Damit gelingt es uns die Eingabeworte für unsere Turingmaschine in eine Zahl zu verwandeln, damit die Registermaschine zu füttern und die Ausgabe dieser (die ja auch eine Zahl ist) wieder in ein Wort zu verwandeln.
Die Standardnummerierung erledigt das. Was uns hier noch fehlt ist die Umwandlung der Flussdiagramm der Turing- in eine passende Registermaschine. Das geschieht wie folgt:
- Aufbereitung der Eingabe: jedes Register bekommt die eindeutige Nummer der Eingabeworte. Nur Register \(R_0\), unser Ausgaberegister bleibt leer. Die Worte der \(k\) Arbeitsbänder werden so alle in die Register abgebildet. Ein Register bekommt also \(\sigma(a)\) zugewiesen, z.B. \(R_1=\sigma(abb)=10\).
- Simulation des Flussdiagramms der Turingmaschine (hier lasse ich die Details erstmal weg, evtl. trage ich sie nach)
Nun können wir auch mit der formalen Definition des Zusammenhangs etwas anfangen:
Sei \(\Sigma\) ein Alphabet, \(\nu_\Sigma : \mathbb{N} \rightarrow \mathbb{N}\) eine Standardnummerierung von \(\Sigma^*\), \(k \in \mathbb{N}\). Es sei \(f : \subseteq \mathbb{N}^k \rightarrow \mathbb{N}\) und \(g : \subseteq (\Sigma^*)^k \rightarrow \Sigma^*\). Dann gilt:
\(f\) berechenbar \(\Longleftrightarrow\) \(\nu_\Sigma f\bar{\nu_\Sigma}^-1 : \subseteq (\Sigma^*)^k \rightarrow \Sigma^*\) berechenbar.
\(g\) berechenbar \(\Longleftrightarrow\) \(\nu_\Sigma^-1 g\bar{\nu_\Sigma} : \subseteq \mathbb{N}^k \rightarrow \mathbb{N}\) berechenbar.
Harter Tobak. Der Satz besagt eig. nichts anderes, als dass
Die Wortfunktion \(g\) genau dann berechenbar ist, wenn ihre Verschlüsselung \(\nu_\Sigma^-1 g\bar{\nu_\Sigma}\) eine berechenbare Zahlenfunktion ist
und
Die Zahlenfunktion \(f\) genau dann berechenbar ist, wenn ihre Verschlüsselung \(\nu_\Sigma f\bar{\nu_\Sigma}^-1\) eine berechenbare Wortfunktion ist.
Also genau das, was wir oben bereits beschrieben haben. Versuchen wir dass mal anhand eines Beispiels aufzudröseln:
Beispiel: \(\Sigma := \{a,b\}\), \(\nu_\Sigma : \mathbb{N} \rightarrow \Sigma^*\) mit der Ordnungsfunktion \(a: \{1,…,n\} \rightarrow \Sigma\),
d.h. \(a\) ist wieder unser \(1\). und \(b\) unser \(2\). Element in der Ordnung.
Wir definieren \(f\) und \(g\) willkürlich:
\(f(x)\begin{cases} {} & 1, \mbox{ wenn } x = 2 \\{} & 2, \mbox{ wenn } x = 1 \end{cases}\)
\(g(x)\begin{cases} {} & a, \mbox{ wenn } x = b \\{} & b, \mbox{ wenn } x = a \end{cases}\)
Wir müssen uns anschauen, was \(\nu_\Sigma^-1 g\bar{\nu_\Sigma}\) und \(\nu_\Sigma f\bar{\nu_\Sigma}^-1\) aus der Definition von oben denn nun tatsächlich tun.
Fangen wir mit \(\nu_\Sigma^-1 g\bar{\nu_\Sigma}\) an, denn es liefert uns zu der Nummer des Definitionswertes (ein Wort) die Nummer des Bildes/Funktionswerts (ja eig. auch ein Wort):
Wir machen uns zunächst einmal klar, dass \(\nu_\Sigma(1) = a\) ist, denn \(a\) ist das erste Element und \(\nu_\Sigma\) gibt uns zu einer Zahl das Wort aus. Die Inverse wäre dann \(\nu_\Sigma^-1(a) = 1\), zu einem Wort bekommen wir also seine eindeutige Nummer.
Und lasst euch von \(\nu_\Sigma^-1 g\bar{\nu_\Sigma}(i)\) nicht erschrecken. Es ist nur eine Komposition aus den oben genannten Funktionen und sieht geklammert weniger bedrohlich aus: \(\nu_\Sigma^-1 (g(i))\). Aber der Reihe nach.
Unserer oben definierten Funktion \(g\) nach, ist z.B. \(g(a) = b\). Zu dem Definitionswert \(a\) bekommen wir also das Bild/den Funktionswert \(b\). Was tun wir nun wenn wir statt auf Worten (was \(a\) und \(b\) ja selbstredend sind) nun auf den zugehörigen Zahlen rechnen wollen? Die Funktionalität der Ursprungsfunktion soll dabei natürlich erhalten bleiben. Und genau das geht mit unserem \(\nu_\Sigma^-1 g\bar{\nu_\Sigma} (i)\), was ja nur – wie gesagt – eine Komposition von Funktionen ist.
Wir tun das, was wir wollten (auf den Zahlen der Worte \(a\) und \(b\) rechnen statt auf den Worten selbst) und setzen \( i = 1\), da der Zahlenwert unseres Arguments \(\nu_\Sigma^-1(a)=1\) ist und dröseln auf:
\(\begin{array}{lcl}\nu_\Sigma^-1 g\nu_ \Sigma(1)&=&\nu_\Sigma^-1 (g (\nu_ \Sigma(1)))&\mbox{Ausklammern fuer bessere Lesbarkeit}&\\ {}&=&\nu_\Sigma^-1 (g (a))&\mbox{da }\nu_ \Sigma(1) = a \mbox { ist}&\\ {}&=&\nu_\Sigma^-1 (b) &\mbox{da } g (a) = b \mbox { ist}&\\ {}&=&2&\mbox {da }\nu_\Sigma^-1 (b) = 2 \mbox { ist}&\end{array}\)
Ergebnis passt? Passt!
Damit haben wir dank unserer Standardnummerierung unsere Wortfunktion \(g\) in eine Zahlenfunktion überführt und können ruhigen Gewissens erneut sagen:
Die Wortfunktion \(g\) ist berechenbar gdw. ihre Verschlüsselung \(\nu_\Sigma^-1 g\bar{\nu_\Sigma}\) eine berechenbare Zahlenfunktion ist.
Damit kann man nun eine Zahlenfunktion angeben, welche statt \(a\) auf \(b\) abzubilden nun eine \(1\) auf eine \(2\) abbildet. Ist diese berechenbar, so ist auch eine Wortfunktion berechenbar.
Analog geht der gleiche Spaß mit \(\nu_\Sigma f\bar{\nu_\Sigma}^-1\), was unsere Zahlenfunktion \(f\) in eine Wortfunktion verschlüsselt. Wir setzen statt \( i = 1\) nun einfach \(i=a\) und schauen ob wir \(b\) herausbekommen.
\(\begin{array}{lcl}\nu_\Sigma f\bar{\nu_\Sigma}^-1(a)&=&\nu_\Sigma(f(\bar{\nu_\Sigma}^-1(a)))&\mbox{Ausklammern fuer bessere Lesbarkeit}&\\ {}&=&\nu_\Sigma(f(1))&\mbox{da }\bar{\nu_\Sigma}^-1(a) = 1 \mbox { ist}&\\ {}&=&\nu_\Sigma(2) &\mbox{da } f (1) = 2 \mbox { ist}&\\ {}&=&b&\mbox {da }\nu_\Sigma(2) = b \mbox { ist}&\end{array}\)Wow! Was man mit den natürlichen Zahlen alles anstellen kann! Wir haben unsere Zahlenfunktion \(f\) nun in eine Wortfunktion verschlüsselt und schließen unser Beispiel mit folgenden Worten ab:
Die Zahlenfunktion \(f\) ist berechenbar gdw. ihre Verschlüsselung \(\nu_\Sigma f\bar{\nu_\Sigma}^-1\) eine berechenbare Wortfunktion ist.
That’s it.
Antwort zum Lernziel: mittels Standardnummerierung ist es uns möglich Worte in Zahlen und Zahlen in Worte bijektiv zu verschlüsseln. Da Register- und Turingmaschinen über Flussdiagrammen definiert sind, können wir diese ineinander simulieren und durch die Standardnummerierung so mit Registermaschinen auf Worten und mit Turingmaschinen im Endeffekt auf Zahlen arbeiten.
Lernziel 3
Definition der primitiv-rekursiven Funktionen
Im Beitrag über primitiv rekursive Funktionen und LOOP Berechenbarkeit haben wir das Thema bereits behandelt. Daher nur ein kurzer Abriss der Definition:
Eine Funktion \(f:\mathbb{N}^k\rightarrow\mathbb{N}\) heißt primitiv-rekursiv wenn sie sich in endlich vielen Schritten aus der menge der Grundfunktionen durch wiederholtes Anwenden der Substitution und primitiver Rekursion erzeugen lässt.
Diese Menge nennen wir \(PRK\).
PS: sie sind alle total (wichtig!) und eine echte Teilmenge der \(\mu\)-rekursiven Funktionen (kommen wir später noch darauf zurück).
Die im Skript genannten Grundfunktionen sind:
- Null- und einstellige Nullfunktion
- Nachfolgefunktion
- Projektion
Alle Funktionen, die wir damit und durch wiederholtes Anwender der primitiven Rekursion und Substitution erstellen können, sind ebenfalls primitiv-rekursiv aufgrund der Abgeschlossenheit. Beispiele zu diesen findet Ihr im oben verlinkten Beitrag.
Wir hatten das bereits im Beitrag zur \(LOOP\)-Berechenbarkeit ausgearbeitet, es sei dennoch der Vollständigkeit halber darauf hingewiesen:
Eine Funktion \(f\) ist \(LOOP\)-berechenbar genau dann wenn sie primitiv-rekursiv ist.
Nicht vergessen. 😉
Antwort zum Lernziel: die Menge der primitiv-rekursiven Funktionen \(PRK\) wird mittels der oben genannten Grundoperationen und wiederholtes Anwenden der Substitution (\(Sub\)) und primitiver Rekursion (\(Prk\)) gebildet. Es sind alles totale Funktionen (d.h. überall definiert) und bilden eine Teilmenge der \(\mu\)-rekursiven Funktionen.
Lernziel 4
Beweis, dass bestimmte Funktionen primitiv-rekursiv sind
In dem oben verlinkten Beitrag könnt Ihr euch die Details dazu zu Gemüte führen. Wir zeigen dort, dass die Addition primitiv-rekursiv ist.
Antwort zum Lernziel: Für den Beweis, dass eine Funktion primitiv-rekursiv ist wird diese einfach mittels der Grundoperationen (oder der als primitiv-rekursiv bereits bewiesenen anderen Operationen) nachgebildet. Damit gilt die Funktion für ein \(n\) als bewiesen. Mittels vollständiger Induktion wird es dann auch für \(n+1\) gezeigt.
Ex-Lernziel: Rechenzeitsatz
Ebenfalls wird im Skript jedoch der Rechenzeitsatz erwähnt. Der besagt nichts anderes, als dass eine Maschine \(M\), welche eine Funktion \(f: \mathbb{N}^k \rightarrow \mathbb{N}\) für eine Eingabe von \(x_1,…,x_k\) eine bestimmte Anzahl an Schritten rechnet. Die Anzahl der Schritte wird mit \(Zeit_M(x_1,…,x_k)\) bezechnet.
Gibt es diese Anzahl von Schritten, so ist die Funktion \(f\) primitiv rekursiv und die Anzahl der Schritte durch eine Funktion \(A_n\) (\(Zeit_M(x_1,…,x_k) <= c \cdot max(x_1,…,x_k) + c\)) beschränkt. Wir haben hier also nichts weiter als die Beschränkung der Rechenschritte einer Registermaschine beim Berechnen einer Funktion abhängig vom Eingabewert der Funktion, einer Konstanten und einer anderen primitiv rekursiven Funktion. Im Skript wird \(A_n\) als Funktion verwendet, aber Achtung: das ist nicht die Ackermann-Funktion, denn diese ist nicht primitiv rekursiv und \(A_n\) muss primitiv rekursiv sein!
Alle Funktionen, die sich auf einer Registermaschine nicht in \(c \cdot 2^x + x\) (Exponentialzeit) berechnen lassen, gelten lt. Skript als „nicht in der Praxis berechenbar“. Damit sind alle in der Praxis berechenbaren Funktionen primitiv rekursiv. Die Isomorphie von Graphen ist z.B. in Exponentialzeit berechenbar, aber es ist noch nicht bewiesen ob es nicht einen effizienteren Algorithmus gibt.
Lernziel 5
Definition der \(\mu\)-rekursiven Funktionen
Auch das haben wir bereits in einem Eintrag für die \(\mu\)-rekursiven Funktionen bereits behandelt. Wir fassen das nochmal in einem Merksatz zusammen:
Die ggf. partielle Funktionen (d.h. sie sind ggf. nicht überall definiert: Beispiel Wurzelfunktion) \(f\) ist \(\mu\)-rekursiv wenn sie mittels der Grundoperationen: Nachfolge-, null- und einstellige Funktion sowie durch wiederholtes Anwenden der Substitution, primitiver Rekursion und des \(\tilde{\mu}\)-Operators abbilden lässt.
Gemerkt? Die Totalität unserer Funktion \(f\) ist für die \(\mu\)-Rekursion nun nicht mehr notwendig. Auch haben wir zusätzlich zu den Grundoperationen, der Substitution und der primitiven Rekursion nun mit dem \(\mu\)-Operator das Nullsetzen der Funktion mit drin.
Aber Achtung: der \(\mu\)-Operator ist im Skript nur auf totalen Funktionen definiert. Bei partiellen Funktionen können wir in Endlosschleifen geraten, aus denen wir sonst nicht mehr herauskommen. Durch eine kleine Erweiterung können wir aber auch auf partiellen Funktionen arbeiten (siehe hier). Ich schreibe dann später noch ein par Kleinigkeiten dazu sobald ich alle Kurseinheiten nochmal überarbeite.
Merke: während man die primitiv rekursiven Funktionen also in \(WHILE\)-Schleifen nachbilden kann, kann man \(\mu\)-rekursiven Funktionen nur in \(WHILE\)-Schleifen und nicht in \(LOOP\)-Schleifen nachbilden. Das liegt daran, dass die Anzahl der Iterationen bei der primitiven Rekursion im Vorfeld bekannt ist (FOR 1 TO 5 DO X) und bei der \(\mu\)-Rekursion (DO X WHILE i NOT 0) nicht. Dieses „Nullstellen“ unserer Funktion besorgt uns der \(\mu\)-Operator.
Update: Ein ausführliches Beispiel mittels partieller Subtraktion zum Nullsetzen habe ich im oben verlinkten Beitrag zur \(\mu\)-Rekursion selbst gebracht. Dort wurde gezeigt, wie man die \(\mu\)-Rekursion anwendet um eine Funktion, die nicht mittels primitiver Rekursion (LOOP) berechenbar ist, als berechenbar nachzuweisen.
Es stellt sich die Frage, warum der \(\mu\)-Operator auf totalen Funktionen definiert ist und der \(\tilde{\mu}\)-Operators auch auf partiellen Funktionen arbeiten kann.
Beispiel \(f:\subseteq\mathbb{N}\rightarrow\mathbb{N}\) mit \(f(x)=\sqrt{x}\) als \(\mu\)-berechenbar nachweisen
Was müssen wir hier tun? Offensichtlich ist \(\sqrt{x}\) auf den natürlichen Zahlen partiell, denn \(\sqrt{5}=div\), da das Ergebnis keine natürliche Zahl ist. Wenn wir diese Funktion nun als \(\mu\)-rekursiv nachweisen wollen, müssen wir folgendes tun:
Wir basteln uns durch „Nullsetzen“ aus unserer Wurzelfunktion \(f\) eine neue Funktion \(h\), die uns in Abhängigkeit von \(y\) eine \(0\) ausgibt wenn \(\sqrt{x}\) korrekt berechnet wurde und ansonsten etwas anderes als eine \(0\) als Ergebnis hat. Kann die Berechnung nicht korrekt abgeschlossen werden, erhöht \(\mu\) auf \(h\) das \(y\) und läuft ewig weiter.
Sie darf aber kein undefiniertes Ergebnis bringen, da wir ansonsten mit dem nächsten \(y\) nicht fortfahren könnten. Das ist der Grund, warum der \(\mu\)-Operator nur auf totalen Funktionen definiert ist. Wäre die „nullgesetzte“ Funktion \(h\) nicht total, hätte das einen Abbruch zur Folge und unser \(\mu\) würde uns nichts brauchbares liefern.
Die aus daraus entstehende Funktion \(\tilde{\mu}(h)(x)\) ist aber partiell. Denn wir bekommen das Ergebnis, die kleinste Nullstelle, nur dann wenn die Berechnung in Ordnung war. Ansonsten läuft unser \(\mu\) ja durch die Totalität von der „nullgesetzten“ Funktion endlos weiter und wir kommen nie zum Stillstand.
Formal ausgedrückt wäre dies:
\(\tilde{\mu}(h)(x)=\begin{cases}0\text{ wenn }\sqrt{x}\text{ existiert}\\div\text{ sonst}\end{cases}\)
Damit ist \(\tilde{\mu}\) partiell.
PS: betrachtet \(\tilde{\mu}(h)(x)\) bitte als „Die aus \(h\) entstehende Funktion„, d.h. als komplettes Gebilde und nicht als Funktion \(\tilde{\mu}\) auf \(h\) auf \(x\).
Schaut euch, wie gesagt, noch einmal ein konkretes Beispiel zur partiellen Subtraktion hier an. Dort seht Ihr auch, wie man eine Funktion nullsetzen kann.
Antwort zum Lernziel: die \(\mu\)-rekursiven Funktionen können – im Gegensatz zu primitiv-rekursiven – auch partiell sein. Sie werden ebenfalls durch die gleichen Grundoperationen und Substitution und primitive Rekursion gebildet wie die primitiv rekursiven Funktionen.
Durch den \(\mu\)-Operator jedoch wird eine Möglichkeit geschaffen die Anzahl der Schleifendurchläufe, nicht von Anfang an festlegen zu müssen (wie das bei der primitiven Rekursion der Fall ist), indem man die Funktion „Nullsetzt“ und mit dem \(\mu\)-Operator die erste Nullstelle sucht.
Es gibt damit Funktionen, die mittels \(WHILE\)-Schleife implementierbar, aber nicht primitiv-rekursiv sind (Ackermann-Funktion z.B.). Die Klasse der implementierbaren Funktionen ist damit größer als die Klasse der primitiv-rekursiven Funktionen.
Lernziel 6
Erläuterung der Churchschen These
Etwas Vorarbeit: es gibt zunächst einen großen Unterschied zwischen maschinell berechenbar und Register-(und damit auch Turing-)berechenbar. Worin liegt der?
Nehmen wir als Beispiel die Ackermann-Funktion. Wir können sie implementieren und wissen daher, dass sie (\(WHILE\)-)berechenbar ist und mit einer Turing- oder Registermaschine berechnet werden kann.
Wollt Ihr mal \(Ackermann(10)\) berechnen? Macht das mal. Und dann könnt Ihr hier weiterlesen. Okay, das war gemein: es gibt keinen Rechner, der genügend Speicher hätte diese Zahl zu speichern. Ebenfalls würde selbst das Alter des Weltalls nicht ausreichen um einen Speicher mit dieser Zahl zu füllen (Satz geklaut aus dem Skript).
Vielleicht habt Ihr nun eine kleine Vorstellung, was den Unterschied ausmacht zwischen intuitiv berechenbar und maschinell-berechenbar.
In der theoretischen Informatik ist uns diese „maschinelle Berechenbarkeit“ aber nicht wirklich wichtig; wir kümmern uns eher um die erste Eigenschaft: die intuitive Berechenbarkeit. Die Speicherkapazität und die Geschwindigkeit der Maschinen ändert sich und es gibt immer mehr Funktionen, die maschinell berechnet werden können. Aber die (intuitiv) berechenbaren Funktionen ändern sich nicht nicht. Sie können entweder berechnet werden, oder eben nicht.
Kommen wir daher zur Churchschen These selbst (aus der Wikipedia, die aber etwas von der im Skript abweicht. Warum sage ich gleich):
Die Klasse der Turing-berechenbaren Funktionen stimmt mit der Klasse der intuitiv berechenbaren Funktionen überein.
Wir erinnern uns an den Begriff der intuitiven Berechenbarkeit: es gibt einen Algorithmus für eine Funktion \(f:\subseteq X\rightarrow Y\), der die Funktion berechnet. Auch können wir uns auf einstellige Zahlenfunktionen \(f:\mathbb{N}\rightarrow\mathbb{N}\) beschränken, da wir Wortfunktionen mittels der Standardnummerierung in Zahlen codieren können und mehrstellige Zahlenfunktionen letztendlich durch die Cantorsche Paarungsfunktion in einstellige Zahlenfunktionen überführt werden können. Wir betrachten also im Endeffekt nur noch die Einband-Turing- (Wortfunktionen) oder die Registermaschinen (Zahlenfunktionen).Aufgrund der Äquivalenz beider Berechnungsmodelle können wir uns zudem aussuchen, was wir betrachten.
Lange Rede, kurzer Sinn: um uns also nicht mit „maschinell“ und „intuitiv“ auseinandersetzen und den Begriff „maschinell“ alle paar Jahre neu definieren zu müssen, setzen wir einfach „maschinell“ mit „intuitiv“ gleich. Und da wir mit Register- und Turing-Berechenbarkeit (durch die Standardnummerierung) ein Äquivalentes Berechnungsmodell haben, können wir statt dem oben genannten Satz aus der Wikipedia, problemlos auch die Churchsche These aus dem Skript herleiten:
Die Register-berechenbaren Funktionen sind genau die maschinell berechenbaren Zahlenfunktionen.
Deutlich geworden?
Die These bedeutet also nichts anderes, als dass man mit der Turing- oder Registermaschine alle intuitiv/maschinell berechenbaren Funktionen berechnen kann. Sie ist zwar nicht beweisbar, da wir den Begriff „intuitiv berechenbar“ nicht exakt formulieren können, sie wird aber allgemein akzeptiert.
Gelingt es uns ein Computermodell anzugeben, dass Funktionen berechnen kann, die mit der Turingmaschine nicht berechnet werden können, so könnten wir die These widerlegen (Ihr wisst, also was zu tun ist!).
Noch ein paar Hintergrund-Details:
Es ist noch niemandem gelungen eine maschinell-berechenbare Funktion anzugeben, die nicht Turing/Register-berechenbar ist, daher liegt der Schluss nahe, dass wir (ohne Berücksichtigung der Faktoren wie Zeit und Speicher) sagen können, dass die maschinell-berechenbaren Funktionen wirklich genau die intuitiv Register/Turing-berechenbaren Funktionen sind.
Antwort zum Lernziel: Die Churchsche These besagt, dass alle intuitiv bzw. maschinell berechenbaren Funktionen genau die Turing- bzw. Register-berechenbaren Funktionen sind. Sie ist aufgrund des fehlenden Formalismus des Begriffs „intuitiv“ nicht beweisbar, konnte aber auch nicht widerlegt werden.
Lernziel 7
Beweis der Existenz von nicht-berechenbaren Funktionen durch Diagonalisierung
Wir rekapitulieren auch hier (im Beitrag über Entscheidbarkeit könnt ihr euer Wissen darüber auffrischen): eine Menge ist entscheidbar (d.h. rekursiv) wenn für jede Eingabe aus der Definitionsmenge entschieden werden kann, ob sie eine Eigenschaft besitzt oder nicht. Formal ausgedrückt:
Entscheidbar/rekursiv: eine Menge heißt entscheidbar falls die charakteristische Funktion berechenbar ist.
Ich wiederhole hier aus dem oben verlinkten Beitrag die formale Definition:
Eine Menge \( T \subseteq M\) ist entscheidbar/rekursiv wenn die charakteristische Funktion \(\chi_T: M \rightarrow \{0,1\}\) definiert durch
\(\chi_T(t)=\begin{cases} 1, & \mbox{ falls } t \in T \\ 0, & \mbox{ sonst}\end{cases}\)berechenbar ist (Achtung: sie muss berechenbar sein!)
Wir haben also eine definitive Aussage zu einer Eigenschaft eines Elements: wir können für jedes Element entscheiden ob es diese Eigenschaft besitzt oder nicht.
Was wäre so eine entscheidbare Eigenschaft? Die Entscheidung ob eine Zahl \(x\) eine Primzahl ist oder nicht wäre entscheidbar.
Den Begriff der Entscheidbarkeit haben wir aber nur für Mengen definiert. Wir interessieren uns hier aber für Funktionen und wollen zeigen, dass es Funktionen gibt, die nicht berechenbar sind. Wir gehen im Prinzip genauso vor, wie Cantor das in seinem zweiten Diagonalisierungsbeweis getan hat. Im Beitrag über Entscheidbarkeit bekommt Ihr einen Einblick über diese Beweismethode am Beispiel der Mächtigkeit von reellen und natürlichen Zahlen.
Aber wollen wir den Beweis aus dem Skript mal Schritt für Schritt durchgehen und die Diagonalisierung nicht auf Mengen, sondern auf Funktionen anwenden. Was haben wir vor? Wir wollen zeigen, dass es nicht-berechenbare Funktionen gibt. Und so gehen wir dazu vor:
1. Zunächst definieren wir uns eine surjektive Funktion \(\psi\) mit \(\psi:\mathbb{N}\rightarrow P^{(1)}\).Was sie genau macht, zeigen wir gleich.
2. \(\Gamma\) ist das Alphabet der \(WHILE\)-Programme, während \(WP\subseteq\Gamma^{*}\) dann die Menge aller \(WHILE\)-Programme ist. Kann es über \(\Gamma\) auch „Nicht-\(WHILE\)-Programme geben? Sicher: irgendwelches Kauderwelsch, dass aus den Zeichen des Alphabets \(\Gamma\) besteht.
3. Wir Standard-nummerieren auch \(\Gamma^{*}\) mit \(\nu_\Gamma\), diese ist also bijektiv. Alle Worte über \(\Gamma\) haben also eine eindeutige Nummer. Bereits jetzt haben wir das Gefühl, dass in der Menge \(WP\) weniger drin ist, als in der Menge \(\Gamma^{*}\). Aber langsam.
Was haben wir bis jetzt? Die Nummerierung aller Worte über unserem Alphabet \(\Gamma\) mit \(\nu_\Gamma\). Hier ist das Spannende, dass selbstverständlich nicht alle Worte über \(\Gamma\) ein \(WHILE\)-Programm sind (siehe Punkt 2). Es kann auch irgendwelches Kauderwelsch sein. Die Menge der \(WHILE\)-Programme \(WP\) ist damit eine Teilmenge der Worte über \(\Gamma\): \(WP\subseteq\Gamma^{*}\).
Und wir haben eine „Nummerierung“ der ggf. partiell einstelligen, berechenbaren Funktionen \(f\in{P^{(1)}}\) mittels \(\psi\).
Während wir \(WHILE\)-Programme mit der Eingabe für Registermaschinen (d.h. unsere Registerbelegung) füttern, füttern wir Funktionen einfach nur mit einem Eingabewert. Ist \(P\) unser \(WHILE\)-Programm, so bezeichnet \(AC(\tau(P)(EC(x)))\) die von \(P\) berechnete Zahlenfunktion.
Schon wieder diese Kompositionen. Am besten wir kümmern uns direkt um ein
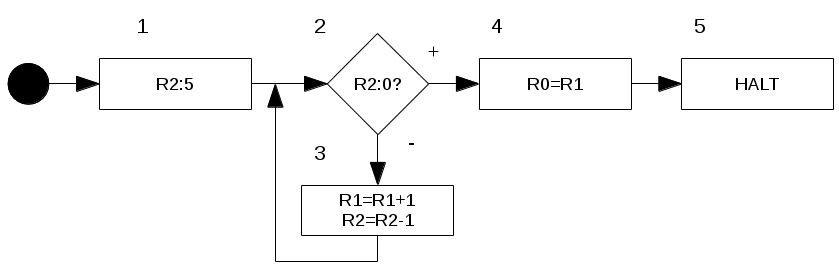
Beispiel: \(f(x)=x+5\)
Diese Funktion \(f\in P^{(1)}\) addiert zu einem Eingabewert \(x\) einfach nur eine \(5\). Das folgende \(WHILE\)-Programm \(W\in{WP}\) tut dies ebenfalls:
i=5; WHILE \(i\neq 0\) DO
x=x+1;
i=i-1;
END;
Da die \(WHILE\)-Programme mittels Register- oder Turingmaschinen definiert werden, brauchen wir ein passendes Flussdiagramm \(F\):
Seht Ihr das Problem?
Das \(WHILE\)-Programm \(W\) können wir nicht einfach mit unserem Funktions-Eingabeparameter \(x\), füttern, sondern brauchen eine Registerbelegung \((R_0,R_1,…)\). Was tun? Unsere Eingabecodierung bemühen, die wir bereits kennen. Wir definieren:
\(EC(x)=(0,x)\)
(nicht vergessen, das 1. Register \(R_0\) bleibt leer, da es unser Ausgaberegister ist).
Soweit so gut. Wir starten unser \(WHILE\)-Programm \(W\) nun mit \(W(EC(x))=W((0,x))\) und bekommen als Ausgabe \(W(0,x)=(x+5,x,0)\). Auch hier ist die Ausgabe des Flussdiagramms nicht der Ausgabewert, den wir bei der Funktion \(f\) erwarten!
Ihr ahnt es sicherlich schon: wir brauchen eine Ausgabecodierung und definieren:
\(AC(d_0,d_1,d_2)=d_0\)
Für uns ist also nur das 1. Register spannend.
Und wenn wir uns die Definition von \(\tau(W)\) (damit wird die von \(W\) berechnete Funktion bezeichnet) vor Augen führen, erschließt sich auch direkt unser \(AC(\tau(W)(EC(x)))\). Lassen wir es mal mit \(x=5\) laufen:
\(\begin{array}{}AC(\tau(W)(EC(5)))&=AC(\tau(W)(0,5))\\&=AC(10,5,0)\\&=10\end{array}\)
Done!
Nennen wir also \(AC(\tau(W)(EC(x)))\) die von \(W\) berechnete, einstellige Zahlenfunktion.
Für unser Vorgaben brauchen wir noch eins: \(Z:\mathbb{N}\rightarrow\mathbb{N}\), unsere Nullfunktion. Egal, was wir da rein werfen, wir bekommen immer eine \(0\) heraus: \(Z(n)=0\) für alle \(n\).
Jetzt sind wir gerüstet um \(\psi\) für unser Vorhaben zu definieren:
\(\psi(i):=\begin{cases}AC(\tau(W)(EC(x)))&\text{ falls }\nu_\Gamma(i)\in{WP}\\Z&\text{ sonst}\end{cases}\)Ist ein \(i\) eine Nummer eines legitimen \(WHILE\)-Programms, d.h. es gilt \(\nu_\Gamma(i)\in{WP}\), so berechnet dieses \(WHILE\)-Programm natürlich auch etwas: irgendeine Funktion aus \(P^{(1)}\). Ihre Ausgabe ist (wie wir oben gesehen haben) ja genau \(AC(\tau(W)(EC(x)))\). Und das ist dann unser \(\psi(i)\).
Es kann aber auch Nummern geben, die nicht zu einem \(WHILE\)-Programm gehören (unser oben genanntes Kauderwelsch). Da Kauderwelsch nichts berechnen kann, haben wir auch keine Ausgabe. Wir brauchen aber für unseren Beweis in jedem Fall eine und definieren in diesem Fall einfach, dass wir mit unserer Nullfunktion \(Z\) eine bekommen.
Durch die Surjektivität von \(\psi\) hat jede Funktion aus \(P^{(1)}\) eine zugehörige Zahl und es müsste also auch für die folgende Funktion \(g\) eine Zahl \(i\) geben:
\(g(i):=\begin{cases}1&\text{ falls }\psi(i)(i)=0\\0&\text{ sonst}\end{cases}\)Was ist \(\psi(i)(i)\)? Ganz einfach: \(\psi(i)\) ist die von \(W\) berechnete, einstellige Zahlenfunktion \(AC(\tau(W)(EC(x)))\) wenn es ein richtiges \(WHILE\)-Programm und kein Kauderwelsch ist. Damit ist \(\psi(i)(i)\) einfach nur das \(WHILE\)-Programm mit der Nummer \(i\), welches als Eingabeparameter die Nummer \(i\) bekommt.
Die Bedeutung erschließt sich hier am besten auch an einem
Beispiel:
Nehmen wir an, das obige \(WHILE\)-Programm \(W\) hat die willkürliche Nummer \(561\). Da es ein echtes \(WHILE\)-Programm ist, gilt damit \(\nu_\Gamma(561)\in{WP}\) und
\(\begin{array}{}\psi(561)&=AC(\tau(\nu_\Gamma(561))(EC(x)))\\&=AC(\tau(\nu_\Gamma(561))(0,x))\\&=AC(x+5,5,0)\\&=x+5\end{array}\)
Und nun übergeben wir \(\psi(561)\) die \(561\) als Parameter:
\(\begin{array}{}\psi(561)(561)&=AC(\tau(\nu_\Gamma(561))(EC(561)))\\&=AC(\tau(\nu_\Gamma(561))(0,561))\\&=AC(561+5,5,0)\\&=566\end{array}\)
Damit ist \(\psi(561)(561)=566\).
Und unser \(g\) wäre der obigen Definition nach \(g(561)=0\).
Was würde passieren, wenn \(W\) kein \(WHILE\)-Programm wäre? D.h. \(\nu_\Gamma(561)\notin{WP}\)?
Dann wäre \(\psi(561)(n)=0\) der Definition nach für jedes \(n\). Und \(g\)? \(g\) wäre:
\(g(561)=1\).
Wie wir an dem Beispiel erkennen, ist sichergestellt, dass \(g\) in jedem Fall einen anderen Funktionswert annimmt als \(\psi(i)\) wenn beide Funktionen mit \(i\) gefüttert werden.
Dämmert es euch bereits? Was ist denn \(\psi\) nochmal? Das ist unsere „Nummerierung“ aller einstelligen, berechenbaren Funktionen aus \(P^{(1)}\)! In \(\{\psi(0),\psi(1),…\}\) liegen sie alle drin. Und wo ist \(g\)? \(g\) gehört zweifelsohne auch in die Menge aller einstelligen, berechenbaren Funktionen aus \(P^{(1)}\). Dann liegt es doch sicherlich auch irgendwo \(\{\psi(0),\psi(1),…\}\), oder?
Nein! \(g\) ist von jeder Funktion aus \(\{\psi(0),\psi(1),…\}\) durch seine Definition, dass es immer einen anderen Wert bei \(g(i)(i)\) annimmt als \(\psi(i)(i)\) verschieden, obwohl es definitiv zu \(P^{(1)}\) gehört. Widerspruch!
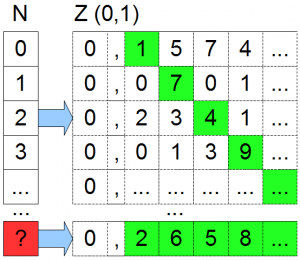
Allgemein beweist man, dass Funktionen nicht berechenbar sind durch Widerspruchsbeweise. Im Skript wird dazu genau das gleiche Verfahren angewandt wie im zweiten Diagonalisierungsbeweis von Cantor: man geht von Vollständigkeit aus, zeigt, dass man noch etwas hinzufügen kann, was sich auf jeden Fall von allen anderen Einträgen unterscheidet (bei Diagonalisierungsbeweisen wird das Diagonalelement eines Eintrags für den neuen Eintrag abgeändert und verändert, so dass beide Einträge mindestens an der abgeänderten Stelle unterschiedlich sind) und stößt so auf einen Widerspruch.
Damit haben wir eine Funktion definiert, die offensichtlich nicht berechnet werden kann. Es folgt: \(g\notin{P^{(1)}}\).
Antwort zum Lernziel: die Angabe einer nicht berechenbaren Funktion gelingt durch Widerspruchsbeweis mittels Diagonalisierung, ähnlich dem Verfahren, das Georg Cantor bereits für sein zweites Diagonalargument angewendet hat um die Überabzählbarkeit der reellen Zahlen zu beweisen.
Dazu wird angenommen, man habe alle berechenbaren Funktionen aufgelistet und zeigt, dass es eine weitere Funktion gibt, die sich definitiv von allen anderen Funktionen unterscheidet. Woraus folgt, dass diese nicht berechenbar sein kann. Zumindest nicht wenn wir Berechenbarkeit mit dem üblichen Begriff für Berechenbarkeit, der Register- und/oder Turing-Berechenbarkeit gleichsetzen.
Das war viel Stoff. Sicherlich sind irgendwo noch Ungenauigkeiten drin oder es haben sich evtl. auch Fehler eingeschlichen. Über Hinweise in den Kommentaren würde ich mich freuen.
Done!