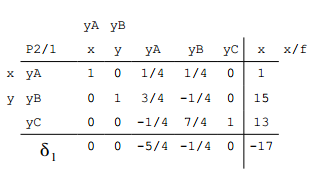Da mich nun mittlerweile die gefühlte 100. Mail erreicht hat, die nach meinem Spickzettel für Algorithmische Mathematik (01142) fragt, habe ich beschlossen meinen Widerstand aufzugeben. Widerstand? Ja, Widerstand. Euch ist bewusst, warum Spickzettel sinnvoll sind? Durch die Anfertigung eines Spickzettels konzentriert man sich über einen längeren Zeitraum auf den Inhalt und seine Aufarbeitung und braucht – oh Wunder! – ihn in der Klausur dann nicht mehr. Das ist der Grund, warum im Wintersemester 09 dieser Spickzettel zu der 150% Klausur von Prof. Dr. Hochstättler zugelassen war (und es wohl noch ist, wie ich den Mails bzgl. meines Spickzettels implizit entnehmen kann).
Durch diesen didaktischen Kniff (und das tolle Skript, Prof. Dr. Hochstättler ist sehr engagiert und nimmt seinen Lehrauftrag äußerst ernst) konnte ich die bisher beste Note in einem mathematischen Fach holen. Daher: Auch wenn Ihr euch meinen Spickzettel herunterlädt, eine kleine Bitte: fertigt zunächst euren eigenen an und schaut euch erst dann meinen an um evtl. fehlende Themen noch aufzunehmen.
Lange Rede, kurzer Sinn: Das war damals meiner.
Und noch ein paar Tipps, die ich bereits an anderer Stelle gegeben habe:
Ihr habt 150% in der Klausur, die auf zwei Stunden ausgelegt ist. Der Schlüssel ist also auch hier: schnell sein. Es gibt sehr schreibintensive Themen, wo Flüchtigkeitsfehler euch Punkte kosten können. Dazu gehören die LU Zerlegung, Chokesly, Dijsktra, Simplex und Optimierung. Hier heißt es: Üben, üben, üben!
Die folgenden Beschreibungen sind ohne Gewähr. Sie sind aus dem WS09, d.h. es ist mittlerweile 3 Jahre her und ich habe mich mit dem Stoff nicht mehr beschäftigt. Sollten sich also Fehler eingeschlichen haben, bitte sofort melden.
SIMPLEX
Der absolute Punktebringer. Aber wehe man verrechnet sich. Daher habe ich mir irgendwann alles haarklein aufgedröselt und ein kleines Howto geschrieben. Alle, die im Stoff bisschen drin sind, sollten das nachvollziehen können. Wie gesagt: ohne Gewähr… ist alles lange her 😉
– Das kleine HowTo zu SIMPLEX gibt es auch als PDF.
– Um nicht immer die Klammern usw. in den Rechnungen zu schreiben, habe ich mir auch eine Simplex Vorlage gebastelt.
Beispiel
1. Das Problem wird in Normalform gebracht
A) Zielfunktion
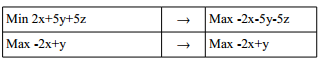
Das Problem wird immer in Maximierungsform dargestellt. Ein Problem in Minimierungsform wird einfach mit (-1) multipliziert.
B) Nebenbedingungen
Die Nebenbedingungen werden in Gleichungsform überführt. Generell ist die Vorgehensweise wie folgt:
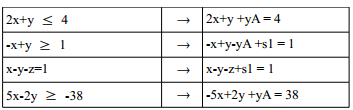
Dabei ist zu beachten, dass als Ergebnis keine negativen Zahlen stehen dürfen. Ist hinter dem Gleichheitszeichen/Ungleichheitszeichen ein negativer Wert, so wird die Un-/Gleichung mit (-1) multipliziert. Dabei dreht sich das $$\leq$$ oder $$\geq$$ entsprechend, das $$=$$ bleibt. Dann wird eine Schlupfvariable ($$yA$$) und eine Hilfsvariable ($$s1$$) eben addiert oder subtrahiert um aus der Ungleichung eine Gleichung zu machen.
Beispiel:
C) Duales Problem (wenn nötig). Beispiel:
2. SIMPLEX Starttableu aufstellen
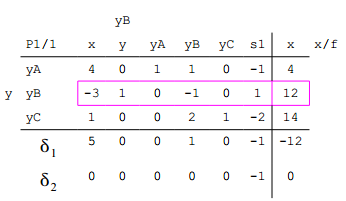
A) Anhand der Normalform wird das Starttableu aufgestellt. Beispiel:
B) Die Auswahl der Pivotspalte geschieht nach folgenden Regeln. Zunächst die Spalte, wo bei einer Zelle in $$\delta_2$$ (Hilfsfunktion) der erste positive Wert steht ($$\delta_2$$, Spalte 2 mit dem Wert „1“). Dann sucht man sich die Zeile mit einem positiven Wert und teilt den x-Wert in dieser Zeile durch den positiven Wert und trägt die Werte in Spalte x/f ein. Die Zeile mit dem niedrigsten Wert beinhaltet den Pivotwert (1).
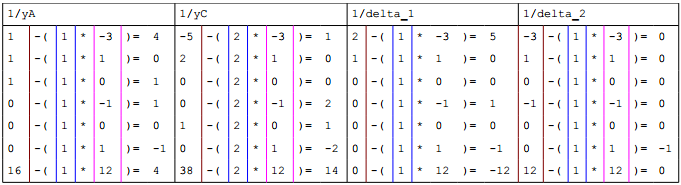
C) Nun wird das 2. Tableu aufgestellt indem man zunächst die Pivotzeile durch das Pivotelement (1) dividiert. Diese bildet die neue Pivotzeile im nächsten Tableu. Für die anderen Zeilen geht man wie folgt vor: man subtrahiert vom alten Zeilenwert (altes Spaltenpivot*neues Zeilenpivot). Ergebnis ist die gleiche Zeile in der neuen Tabelle. Rechnung:
Die Ergebniswerte sind die neuen Zeilen im neuen Tableau. Dabei werden dann $$yB$$ und $$y$$ „im Kopf“ vertauscht.
Das ganze geht so lange, bis in der Zeiler der Hilfsfunktion $$\delta_2$$
keine positiven Werte mehr sind. In diesem Fall ist es bereits jetzt soweit. Somit ist es das Endtableau für Phase 1. Wir beginnen mit
D) dem Aufstellen des Starttableaus für Phase 2
Hier werden nun die Hilfsfunktions-Zeile $$\delta_2$$ und die Hilfsvariablenspalte (s1) gelöscht. Das bringt uns zu folgendem Starttableau für Phase 2.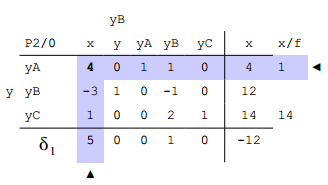
Wir wählen die Pivotspalte und Zeile wieder wie gehabt und führen wieder die übliche Rechnung durch.
Die Rechnung führt uns zu folgender, 1. Tabelle von Phase 2:
Nun stehen nur negative Werte in der Zielfunktionszeile $$\delta_1$$.
Wir können also die Lösung
$$x=1$$
$$y=15$$
mit einem Funktionswert von
$$f(x,y) = 17$$
ablesen. Wäre es eine Minimierungsaufgabe, so müsste man den Funktionswert -17 nicht mit (-1) multiplizieren. Der Funktionswert wäre dann -17.
Hier findet Ihr noch ein kleines, handschriftliches Simplex Beispiel von mir.
CHOLESKY-Zerlegung
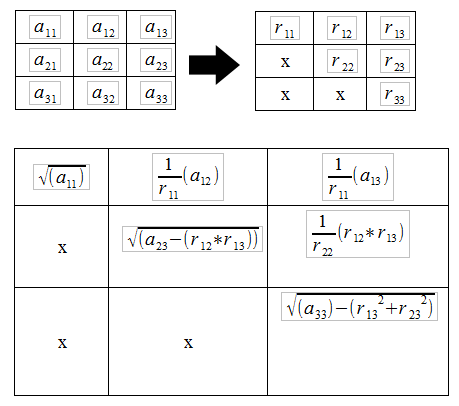
Auch hier gilt: je schneller, desto besser. In den Übungsaufgaben und in der Klausur kommen meist nur 2×2 oder 3×3 Matritzen vor. Dafür habe ich mir damals ganz einfach für jedes Feld eine Formel gebastelt:
3×3 Matrix
That’s it. Die 2×2 Matrix ist – das wollte ich schon immer mal sagen – doch trivial 😀