Wichtig: lasst euch von der mathematischen Definition nicht einschüchtern. Ich versuche in jedem Satz immer die Definition noch zu erklären. Ansonsten: wer grobe Schnitzer findet: bitte melden!
Zwei wichtige Themen aus der 2. Kurseinheit behandeln die primitive und die \(\mu\)-Rekursion. Aus der Definition im Kurstext erschließt sich mir ihre (und von vielem anderen auch) Bedeutung jedoch nicht sofort. Aber vielleicht stehe ich auch einfach auf dem Schlauch bei diesen Themen. Beide Rekursionen dienen dazu das Repertoire der berechenbaren Funktionen zu vergrößern.
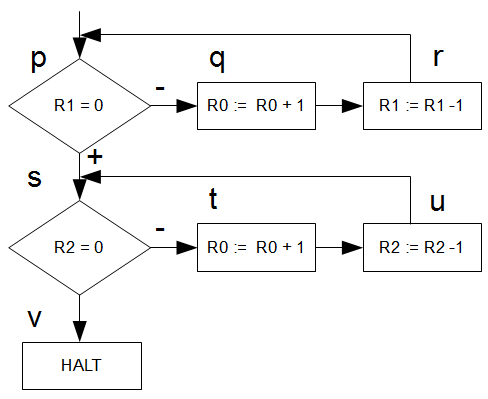
In Kurseinheit 1 gab es ja bereits eine Liste an berechenbaren Funktionen. All‘ diese konnten mit einer einfachen Registermaschine, welche nur die Grundoperationen (Arithmetische Differenz zu 1, Addition von 1 und Test auf 0) abgebildet werden. Das ist zwar alles schön und gut, aber reicht uns natürlich nicht. Also erweitern wir das Feld der berechenbaren Funktionen mit der Rekursion, denn der Definition nach sind alle primitiv- und \(\mu\)-rekursiven Funktionen berechenbar.
Grundoperationen, Komposition, Rekursion
Was ist also die primitive Rekursion? Die primitiv rekursiven Funktionen entstehen aus den Grundoperationen (die stelle ich gleich vor) und werden mittels Komposition (Hintereinanderausführung) und/oder der primitiven Rekursion gebildet. Als Grundoperationen haben wir:
Die konstante Funktion: \(C^k : \mathbb{N}^k \rightarrow \mathbb{N}\) mit \((n_1, …, n_k) \mapsto c\) und \(c \in \mathbb{N}\).
Oder manchmal auch die Nullfunktion \(0^k : \mathbb{N}^k \rightarrow \mathbb{N}\) mit \((n_1, …, n_k) \mapsto 0\)
Erklärung: \(\mathbb{N}^k \rightarrow \mathbb{N}\) bedeutet nichts weiter als dass der Definitionsbereich (und damit die Argumente der Funktion) der Bereich der natürlichen Zahlen (eben \(\mathbb{N}^k\)) ist. \(k\) bedeutet Stelligkeit (also die Anzahl der Argumente der Funktion, die Argumente selbst sind mit \((n_1, …, n_k)\) angegeben). Das Ergebnis der Funktion ist jedoch nur einstellig. Z.B. wäre \(f^3 : \mathbb{N}^3 \rightarrow \mathbb{N}\) mit \(f(x,y,z) = x + y – z\) so eine Funktion (nicht für eine konstante Funktion), die drei Argumente entgegen nimmt, aber nur einen Funktionswert (sogenannter Wertebereich) ausgibt.
Die konstante Funktion \(C^k\) macht noch viel weniger. Egal wieviel Argumente Du ihr gibst, sie gibt immer nur einen Wert zurück. Die Konstante c, welche auch aus dem Bereich \(\mathbb{N}\) kommt. Also z.B. \(f^4 : \mathbb{N}^4 \rightarrow \mathbb{N}\) mit \(f(a,b,c,d) = 5\). Egal, was die Funktion an Argumenten bekommt, es kommt immer 5 heraus.
Die konstante Nullfunktion, welche häufig in den Definitionen für die primitive Rekursion verwendet wird ist auch nur eine konstante Funktion. Nur ist hier \(c\) immer einfach nur 0. Mehr nicht. Also nicht verwirren lassen.
Die Projektion auf ein Argument: \(\pi^k_i : \mathbb{N}^k \rightarrow \mathbb{N}\) mit \((n_1,…,n_k) = n_i\)
Hier ist die Erklärung offensichtlich. Also überspringen wir sie mal. Nein, Scherz. Das muss ich oft genug im Skript lesen und denke mir nur: „Bitte?!“. Manche Dinge sind derart einfach, dass man nicht glaubt sie verstanden zu haben weil man von den ganzen griechischen Buchstaben erschlagen wurde.
Diese Funktion tut nur eines: sie gibt das \(i-te\) Argument aus ihrer \(k\)-stelligen Argumentliste zurück. Das wars. Wirklich. Aber eine Kleinigkeit ist noch hilfreich: Es gibt die einstellige Projektion mit \(\pi^1_1(n_1) = n_1\). Diese nennt man die Identitätsfunktion \(id(x) = x\). Konkretes Beispiel für beide? Bitte sehr. Projektion: \(\pi^4_2(a,b,c,d) = b\). Identitätsfunktion: \(\pi^1_1(a) = id(a) = a\).
Die Nachfolgefunktion: \(Suc : \mathbb{N} \rightarrow \mathbb{N}\) mit \(n \mapsto suc(n) := n+1\)
Geht kaum einfacher. Was macht die Funktion? Sie gibt zu dem ihr gegebenen Argument einfach nur den Nachfolger zurück. Beispiel: \(f(2) = 3\). Das war’s.
Was haben die Basis-Funktionen nun mit primitiver Rekursion zu tun? Alle Funktionen, die aus diesen Basisoperationen mittels Komposition (oder Substitution) und Rekursion gebildet werden können, werden rekursive Funktionen genannt und sind berechenbar. Diese liegen in \(\mathcal{P}\), dem Bereich der total-rekursiven Funktionen, denn sie decken den vollständigen Definitionsbereich ab (jedem Wert aus dem Definitionsbereich wird ein Funktionswert zugeordnet, kein Argument bleibt ohne Funktionswert). Zu den partiell-rekursiven Funktionen kommen wir noch.
Beispiel: Wollen wir mal einen Versuch wagen und eine Komposition der Grundoperationen aufstellen und ausrechnen?
Konstante Funktion: \(c : \mathbb{N}^2 \rightarrow \mathbb{N}\) mit \(c(x,y) \mapsto 4\).
Projektion \(\pi^2_1 : \mathbb{N}^2 \rightarrow \mathbb{N}\) mit \(\pi^2_1 (x,y) \mapsto x\)
Nachfolgefunktion: \(suc : \mathbb{N} \rightarrow \mathbb{N}\) mit \(suc(x) \mapsto x+1\)
Wir bilden nun aus diesen drei Funktionen eine Komposition: \(\pi^2_1(x,y)\circ (c(x,y) \circ suc(x))\). D.h. eine Hintereinanderausführung der Funktionen. Es gilt (bitte beim Wikipedia-Link nachschauen) bei der Komposition: \(g \circ (f \circ h) = g(f(h(x)))\). Für unsere Funktionen bedeutet es also: \(\pi^2_1(c(suc(x),y),z)\). Wir setzen unsere Variablen willkürlich: \(x=5\), \(y=6\) und \(z=7\). Damit haben wir dann auch gleich etwas, womit wir rechnen können: \(\pi^2_1(c(suc(5),6),7)\). Wir beginnen also von Innen nach Außen:
\(suc(5) = 6\) (unsere Nachfolgefunktion)
\(c(6,6) = 4\) (unsere konstante Funktion)
\(\pi^2_1(4,7) = 4\) (unsere Projektion)
Damit ist \(\pi^2_1(c(suc(5),6),7) = 4\).
Nun ist jede Funktion, die wir mit den drei Basisoperationen von oben mittels Komposition (Substitution) und Rekursion abbilden können ebenfalls primitiv-rekursiv und damit berechenbar.
Rekursionsschema
Bitte nicht drüber hinwegweg lesen. Diese Ausführung wird bei jeder Definition der primitiven Rekursion verwendet (manchmal in umgekehrter Reihenfolge, aber der Sinn und Zweck sind gleich). Erst wenn man die Funktion in das Rekursionsschema hat überführen können, ist sie wirklich primitiv rekursiv. Wir werden also mit folgenden Dingen gequält:
1. Komposition/Einsetzung/Substitution formal: haben wir hier z.B. eine Funktion \(h\) (k-stellig mit \(\mathbb{N^k}\)) und mehrere Funktionen \(g_1,…,g_k\) (alle n-stellig mit \(\mathbb{N^n}\)) und sind diese primitiv-rekursiv, so ist auch \(h(g_1(x_1,…,x_n), …, g_k(x_1,…,x_n))\) primitiv-rekursiv.
Das bedeutet: nichts weiter als eine Einsetzung. Zunächst haben wir in der Funktion \(h\) genau \(k\) Parameter (Stelligkeit, siehe oben) aus dem Bereich der natürlichen Zahlen \(\mathbb{N}\). Und dann noch \(k\) Funktionen \(g\) (es können auch mehr sein, aber wir brauchen nur \(k\)), die selbst \(n\) Parameter verwenden, welche oben mit \((x_1,…,x_n)\) beschrieben sind. Nun möchten wir die (nicht beschriebenen) Parameter der Funktion \(h\) einfach durch ausgerechnete Funktionswerte der Funktionen \(g\) ersetzen. Das ist alles, was die Substitution macht.
Beispiel:
Funktion: \(h : \mathbb{N}^2 \rightarrow \mathbb{N}\) mit \(h(x,y) \mapsto x*y\)
Funktion: \(g : \mathbb{N}^3 \rightarrow \mathbb{N}\) mit \(g(a,b,x) \mapsto a+b+c\)
Wir führen nun die Substitution der Parameter von \(h\) mit den Funktionswerten von \(g\) durch: \(h(x,y) = h(g(a,b,c),g(a,b,c))\). Wir setzen willkürlich \(a = b = c = 2\) und haben somit: \(h(g(2,2,2),g(2,2,2))\). Ausrechnen von Innen nach Außen: \(h(6,6) = 36\). That’s it!
2. Rekursionsschema formal: dieser Teil wird dazu verwendet um zu garantieren, dass auch die neue Funktion, welche durch primitive Rekursion gebildet wurde bzgl. primitiver Rekursion abgeschlossen und ist nicht aus dem Rahmen fällt. Es besagt, dass eine Funktion \(f\) nach dem Schema der primitiven Rekursion aufgebaut ist, wen sie folgende Form besitzt:
\(f(m,n)=\begin{cases} g(n), & \mbox{falls }m = 0 \\ h(f(m-1,n),m-1,n), & \mbox{falls }m > 0 \\\end{cases}\)
Was bedeutet das nun für uns? Wir haben hier zwei Fallunterscheidungen: einmal wenn ein Parameter = 0 (m=0) ist, so bedarf es keiner Rekursion und wird durch eine Funktion \(g(n)\) abgehandelt. Ist jedoch \(m > 0\), müssen wir einen zweiten Fall betrachten. Hier erfolgt die Rekursion, welche die Funktion \(f\) einfach nur mit dem nächst-kleineren Parameter \(m-1\) aufruft. Am Ende wird \(m=0\) und wir können unser \(g(n)\) für diesen Fall verwenden und schließen die Rekursion damit ab.
Häufig wird auch folgende Definition verwendet:
(R1) \(f(0,x_1,…,x_n) = g(x_1,…,x_n)\)
Bedeutet nichts anderes, als unser \(g\) von oben. Nur dass das etwas allgemeiner formuliert und die Parameterbeschränkung abgehoben wurde.
(R2) \(f(m+1,x_1,…,x_n) = h(f(m,x_1,…,x_n),m,x_1,…x_n)\)
Auch das ist nicht weit weg von unserer Fallunterscheidung. Unsere Funktion beginnt mit dem Parameter \(m+1\), das ist das was eig. unsere Schleifenvariable ist. Diese wird dann im nächsten Durchlauf dekrementiert und die Funktion ruft sich mit diesem dekrementierten Wert so lange selbst auf, bis \(m=0\) ist und wir unser oben definiertes \(g\) verwenden können. In manchen Definitionen wird einfach nur \(m\) in \(f\) verwendet und in \(h\) steht dann \(m-1\).
Hier wäre ein Beispiel nicht schlecht, oder? Versuchen wir es doch mal mit der Addition und schauen ob sie aus der Klasse der primitiv-rekursiven Funktionen ist. Also los geht’s:
Ist die Addidtion primitiv rekursiv?
Um zu beweisen, dass eine Funktion primitiv rekursiv ist muss man diese mit den obigen Grundoperationen definieren und in das Rekursionsschema pressen können. Und zwar für alle Fälle aus den natürlichen Zahlen. Hier sei die 0 vor allem zu beachten, denn die wird gerne mal vergessen. Im Endeffekt ist die Addition ja nur \(add(m,n) = m+n\). Um zu zeigen, dass sie primitiv rekursiv ist müssen wir sie nun mit den oben definierten Grundoperationen abbilden und sie ins Rekursionsschema pressen. Probieren wir es einfach.
1. Fall: Addition von 0 + n. Bedeutet: \(add(0,n)=0+n = n\). Das bilden wir ab mit der Projektion: \(\pi^2_2 : \mathbb{N}^2 \rightarrow \mathbb{N}\) mit \(\pi^2_2 (0,n) \mapsto n\). Aufgeschrieben bedeutet dies: \(add(0,n)=\pi^2_2 (0,n)=n\). Damit wir unser \(g(n)\) aus dem Rekursionsschema von oben schon erschlagen:
\(add(m,n)=\begin{cases} g(n) = \pi^2_2 (0,n), & \mbox{falls }m = 0 \\ …, & \mbox{falls }m > 0 \\\end{cases}\)Allgemein ausgedrückt (wir wollen uns ja an die Definitionen aus dem Skript halten) pressen wir das nun in unsere Definition von \(g\) aus (R1):
\(f(0,x_1,…,x_n) = add(0,n)\) \(g(x_1,…,x_n)=g(n)=\pi^2_2 (0,n)=n\)Und somit
(R1) \(add(0,n)=g(n)=\pi^2_2 (0,n)=n\)
Passt also in den ersten Teil des Schemas.
2. Fall: Addition von m + n: Bedeutet: \(add(m,n) )= m+n\). Das ist etwas schwieriger. Hier bedienen wir uns der primitiven Rekursion und der Nachfolgefunktion \(suc\): \(add(m+1,n) = suc(add(m,n))\) (Achtung: die Funktion ist noch nicht in der geforderten Form für den 2. Fall um die Übersicht zu wahren). Noch nicht so ganz einleuchtend, oder? Vor allem nicht, wie wir drauf gekommen sind. Nehmen wir einen ganz einfachen Fall mit echten Zahlen.
Wollen wir z.B. 1 + 5 addieren, so fällt uns schnell ein, dass wir uns doch einfach einmal der Nachfolgefunktion bedienen können: \(add(1,5) = suc(add(0,5))\) (nun haben wir Innen den 1. Fall von oben, wo die 0 addiert wird und wir verwenden die dort für diesen Fall definierte Projektion, unser \(g(n)\) auf das zweite Argument) \(=suc(\pi^2_2(0,5)) = suc(5) = 6\). Schnell sollte einleuchten, dass wir uns einfach beliebig oft der Nachfolgefunktion bedienen dürfen, abhängig davon was wir addieren. Wir können hier aber zunächst nur die 1 addieren. Um auch mehr als die 1 addieren zu können, müssen wir die Funktion so definieren, dass sie am Ende auf unser \(g(n)\) Innen zurückgeführt, welches dann mit \(suc(x)\) ausgerechnet werden kann. Wie würde unser \(add(2,5)\) denn aussehen? So: \(suc(suc(\pi^2_2(0,5))) = suc(suc(5))\). Lösen wir das auf: \(suc(suc(5)) = suc(6) = 7\). Und \(add(3,5)\)? Genau! \(suc(suc(suc(\pi^2_2(0,5)))) = suc(suc(suc(5))) = 8\).
Das ist aber noch nicht die Rekursion, denn eine Rekursion ist der Aufruf einer Funktion durch sich selbst. Und vor allem ist das ja auch noch nicht in der streng geforderten Form! Wir können ja nicht für jeden \(n\) aus \(\mathbb{N}\) tausende von \(suc\) angeben. Also muss unser \(add\) rekursiv durch sich selbst definiert werden (was ja am Ende sowieso auf ein einzelnes \(suc\) zurückführt). Probieren wir also das Beispiel mit den Zahlen \((3,5)\) von oben und arbeiten mit Rekursion statt nur mit tausenden von \(suc\):
\(\begin{array} {lcl} add(3,5)&=& suc(add(2,5))\\&=& suc(suc(add(1,5)))\\&=&suc(suc(suc(add(0,5))))\\&=&suc(suc(suc(\pi^2_2(0,5))))\\&=&suc(suc(suc(5)))\\&=&suc(suc(6))\\&=&suc(7)\\&=&8\end{array}\)Damit entspricht das genau dem, was wir mit \(add(m+1,n) = suc(add(m,n))\) bereits rekursiv definiert haben. Für die einfache Fallunterscheidung nehmen wir dann \(add(m,n) = suc(add(m-1,n))\), was ja das Selbe ist. Für die allgemeinere Definition aus (R2) ist unsere Definition jedoch goldrichtig.
Ab damit in die Fallunterscheidung und wir haben unser \(h\) gefunden:
\(add(m,n)=\begin{cases} g(n)=\pi^2_2 (0,n), & \mbox{falls }m=0 \\ suc(\pi^3_1 (add(m-1,n),m-1,n)) & \mbox{falls }m > 0 \\\end{cases}\)Wie versprochen werden wir auch hier allgemeiner und pressen das in unsere Definition der Rekursion für (R2):
(R2) \(f(m+1,x_1,…,x_n)=add(m+1,n)\)
\(h(f(m,x_1,…,x_n),m,x_1,…x_n) = suc(\pi^3_1(add(m,n),m,n))\)Und somit
(R2) \(add(m+1,n) = suc(\pi^3_1(add(m,n),m,n))\)
Und das passt auch in den zweiten Teil des Schemas.
Nehmen wir Papier und Stift und rechnen damit ein konkretes Beispiel durch:
Beispiel: \(add(3,4)\)
Mit unserer Definition der Addition von oben \(add(m+1,n)=suc(\pi^3_1 (add(m,n),m,n))\) können wir das nun rekursiv auflösen:
\(\begin{array} {lcl} add(3,4)&=& suc(\pi^3_1 (add(2,4),2,4))\\&{}&\text{(aufloesen von add(2,4))}\\&=& suc(\pi^3_1 (suc(\pi^3_1(add(1,4),1,4),2,4)))\\&{}&\text{(aufloesen von add(1,4))}\\&=&suc(\pi^3_1 (suc(\pi^3_1(suc(\pi^3_1(add(0,4),0,4),1,4),2,4))))\\&{}&\text{(aufloesen von add(0,4))}\\&=&suc(\pi^3_1 (suc(\pi^3_1(suc(\pi^3_1(\pi^2_2(0,4),0,4),1,4),2,4))))\\&{}&\text{(aufloesen von }\pi^2_2(0,4))\\&=&suc(\pi^3_1 (suc(\pi^3_1(suc(\pi^3_1(4,0,4),1,4),2,4)))\\&{}&\text{(aufloesen von }\pi^3_1(4,0,4))\\&=&suc(\pi^3_1 (suc(\pi^3_1(suc(4),1,4),2,4)))\\&{}&\text{(ausrechnen von } suc(4))\\&=&suc(\pi^3_1 (suc(\pi^3_1(5,1,4),2,4)))\\&{}&\text{(aufloesen von }\pi^3_1(5,1,4))\\&=&suc(\pi^3_1 (suc(5),2,4)))\\&{}&\text{(ausrechnen von } suc(5))\\&=&suc(\pi^3_1 (6,2,4))\\&{}&\text{(aufloesen von }\pi^3_1 (6,2,4))\\&=&suc(6)\\&{}&\text{(ausrechnen von } suc (6))\\&=&7\end{array}\)
Damit haben wir die Addition primitiv rekursiv definiert, die Addition ist also ein Teil der primitiv-rekursiven Funktionen und damit berechenbar. Sicher wollt ihr den ganzen Spaß auch mit der Multiplikation machen. Probiert es mal. Ihr werden sehen, dass es schnell unübersichtlich wird wenn ihr nur die 3 Grundoperationen von oben benutzt. Irgendwas stimmt hier aber noch nicht ganz, oder? Euch schwirrt bestimmt noch etwas aus der 1. Kurseinheit im Kopf rum, was wir gemacht haben. Genau! Erinnert ihr euch zufällig noch an die normalen und verallgemeinerten Registermaschinen aus der 1. Kurseinheit?
Alle Operationen, die wir mit normalen Registermaschinen abbilden und damit ihre Berechenbarkeit beweisen konnten, konnten wir fortan in unseren verallgemeinerten Registermaschinen ohne Beweis benutzen! Das Gleiche können wir hier auch tun. Wir können jetzt die Multiplikation primitiv-rekursiv definieren und hierfür die Addition verwenden, deren Berechenbarkeit wir soeben nachgewiesen haben. Weil wir dann damit nach dem Rekursionsschema die Multiplikation mittels der Addition definieren konnten, die Addition durch die 3 Grundoperationen definiert wurde folgt daraus, dass die Multiplikation auch berechenbar ist.
Gerne kann ich den Lösungsweg für die Multiplikation dann auch posten wenn gewünscht. Versucht es aber erstmal selbst.
Ackermann-Funktion
Aber auch die primitive Rekursion hat ihre Grenzen. Genau für diese wurde die Ackermann-Funktion erfunden. Man vermutete vor einiger Zeit, dass man mit der Klasse der primitiv Rekursiven Funktionen alle berechenbaren Funktionen erschlagen hätte. Das wurde jedoch von der Ackermann-Funktion, die eigens dafür entwickelt wurde, widerlegt. Das Repertoire an Grundoperationen war schlicht und ergreifend nicht mächtig genug um diese berechenbare, aber nicht primitiv rekursive Funktion abzubilden.
Erst mit der Einführung des \(\mu\)-Operators und der sogenannten \(\mu\)-Rekursion hat man diese Klasse so erweitern können, dass die Ackermann-Funktion da hinein fällt. Man geht in der Church’schen These davon aus, dass sich mit der \(\mu\)-Rekursion nun alle berechenbaren Funktionen abbilden lassen, die (Turing-)berechenbar sind. Aber da kümmern wir uns dann im nächsten Beitrag im Rahmen der \(\mu\)-Rekursion drum.
Loop Berechenbarkeit
Eine wichtige Eigenschaft der rekursiven Funktionen ist derer Zusammenhang mit der LOOP-Berechenbarkeit. Jedes LOOP-Programm lässt sich primitiv rekursiv darstellen und umgekehrt. Im Gegensatz zu GOTO (Registermaschinen) und WHILE (unsere \(\mu\)-Rekursion) terminieren LOOP-Programme immer. Und ja, Ihr habt es euch vielleicht gedacht: die Ackermann-Funktion ist nicht primitiv rekursiv und damit auch nicht LOOP-berechenbar.
Aber hier steht schon zu viel Text. Vielleicht sind WHILE und LOOP-Berechenbarkeit ja einen eigenen Beitrag wert 🙂
Update
Gesagt, getan: der neue Beitrag behandelt die \(\mu\)-Rekursion und die WHILE-berechenbarkeit. Auch wenn ich das bereits etwas vorweg nehme, ein wichtiger Merksatz um es auf den Punkt zu bringen:
Merksatz: jedes LOOP-Programm lässt sich durch primitive Rekursion ausdrücken un jede primitiv rekursive Funktion durch ein LOOP-Programm. Ebenso lässt sich ein LOOP-Programm durch ein WHILE-Programm ersetzen. Damit ist auch jede primitiv rekursive Funktion WHILE-Berechenbar. Jedoch gilt das nicht umgekehrt: WHILE-Schleifen lassen sich nicht durch LOOP-Schleifen ersetzen (es ist z.B. im Voraus nicht bekannt wie häufig die Schleife durchlaufen wird), siehe Ackermann-Funktion. Erst durch die \(\mu-Rekursion\) können wir das WHILE-Konstrukt mathemathisch greifbar machen.