TIB: NP-Vollständige Probleme (Lernziele KE4 2/2, Update)

Lernziel 3

Wie ist der Vollständigkeitsbeweis zu $SAT$?

$SAT$ steht für das englische satisfiability. Also ein Erfüllbarkeitsproblem. Es wird gefragt ob eine aussagenlogische Formel erfüllbar ist (erinnert ihr euch an KNF/DNF aus der technischen Informatik? Das hier ist nicht weit weg...).

Da eine Formel nur endlich viele variablen enthält, die nur mit $1$ und $0$ belegt werden können, haben wir eine endliche Anzahl an Möglichkeiten. Wenn wir alle durchprobieren, kommen wir (oder nicht) irgendwann dahin, dass die Formel wahr wird. Haben wir $n$ Variablen, so müssen wir im worst case $2^n$ Kombinationen betrachten. Damit benötigen wir für $SAT$ einen Exponentialzeitalgorithmus und diese gelten für die Praxis als unwichtig, steigt der Aufwand für größere $n$ doch massiv an. Hätten wir zu dem Problem einen Polynomialzeitalgorithmus, sähe die Sache ganz anders aus.

Aber es gibt einen Lichtblick: Wenn wir nicht jede Möglichkeit durchprobieren wollen, kann das Prüfen einer vorgegebenen Lösung für $SAT$ in Linearzeit erfolgen. Haben wir $n$ Variablen, so müssen wir sie erst kurz belegen und die Formel dann auswerten. Beides geht jeweils in Linearzeit. Damit haben wir schon einmal den ersten Schritt getan: wir haben eine $KTM$ angegeben, die die Hilfseingabe (unsere zu prüfende Belegung der $n$ Variablen) auf wahr oder falsch kontrolliert. Okay, haben wir nicht. Aber wir könnten es mit wenig Aufwand (vielleicht reiche ich so eine $KTM$ bei Gelegenheit hier nach) tun. Damit ist der erste Schritt vollbraucht $SAT\in NP$.

Kümmern wir uns nun um den zweiten Schritt, die $NP$-Härte. Aber ohne die Abkürzung der Reduktion zu nehmen. Das folgende Beispiel basiert auf dem Buch von Prof. Dr. Dirk W. Hoffmann (oben rechts verlinkt). Die Credits also ausnahmslos an ihn. Und auch wenn ich mich wie eine kaputte Schallplatte anhöre: das Buch ist ein Lifesaver für theoretische Informatik und gehört in jedes IT-Bücherregel, daher absolute Kaufempfehlung. Der Herr gehört unbedingt unterstützt.

Wir müssen hier also beweisen, dass wir ausnahmslos alle Probleme aus $NP$ auf $SAT$ reduzieren können. Da wir keines haben, müssen wir uns eins basteln, wo einzusehen ist, dass es alle Probleme aus $NP$ "widerspiegelt" und dieses auf $SAT$ reduzieren. Nehmen wir also ein beliebiges Problem $L\in NP$ und eine $TM$ namens $T$, die das Problem entscheidet. Wir müssen jetzt zeigen, dass wir für jedes Eingabewort $\omega$ für $T$ eine Formel $F$ konstruieren können, für die gilt:

$T(\omega)$ terminiert im Endzustand $\Leftrightarrow F(\omega)$ ist erfüllbar.

D.h. nur wenn unsere Maschine mit dem Eingabewort terminiert, so ist auch unsere Formel mit dem gleichen Eingabewort erfüllbar und andersrum. Wir müssen $F$ in polynomieller Zeit konstruieren. Dazu werden zunächst Variablen eingeführt:

$B_{i,k,\sigma}=1$ Nach $i$ Schritten, steht an Position $k$ das Zeichen $\sigma$.

$S_{i,S}=1$ Maschine $T$ befindet sich nach $i$ Schritten im Zustand $S$.

$P_{i,k}=1$ Maschine $T$ befindet sich nach $i$ Schritten auf Bandposition $k$.

Die Laufzeit der Maschine ist polynomiell durch das Polynom $p(n)$ beschränkt, denn $n$ ist die Länge der Eingabe $\omega$. Die Indizes von $i,s$ liegen also im Intervall $[0;p(n)]$. Auch bewegt sich der Schreib-Lese-Kopf maximal $p(n)$ Positionen nach links oder rechts, so dass wir den Bandinhalt auf dem Teilstück $-p(n),...,p(n)$ betrachten müssen. Der Kopf steht über der Position $0$. Ausprobiert wird das an der Sprache $L:=\{\#^n\mid n\in{\mathbb{N}}\}$ mit dem Alphabet $\Sigma=\{\#\}$.

Diese Sprache wird von einer $TM$ erkannt, die nur zwei Zustände hat. $s_0$ wenn das Zeichen auf dem Band eine $\#$ ist (Eingabewort $\omega\in L$) und $s_1$ wenn es ein $B$ (Blank) ist. Da die Berechnung hier bereits nach einem Schritt endet, ist die Laufzeit der Maschine $p(n)=1$. Wir haben also ein "Problem", dass in polynomieller Zeit durch die $T$ entschieden werden kann und damit in $P$ liegt (das $N$ ist ja nur das Orakeln der Eingabe). Nun müssen wir $T$ nur noch polynomiell in eine $SAT$-Instanz codieren.

Um den Bandzustand, den Zustand der Maschine und die Position des Lesekopfes als eine Formel zu codieren, werden die oben eingeführten Variablen verwendet. Ist z.B. $B_{0,1,\#}=1$, so befindet sich auf dem Band jetzt auf Position $1$ das Zeichen $\#$. Durch die oben gemachten Einschränkungen, haben wir $12$ verschiedene Bandvariablen, die wir mit $0$ oder $1$ belegen können um den Bandzustand zu repräsentieren ($B$ ist das Blank).

$B_{0,-1,B},B_{0,-1,\#},B_{1,-1,B},B_{1,-1,\#}$

$B_{0,1,B},B_{0,1,\#},B_{1,1,B},B_{1,1,\#}$

$B_{0,0,B},B_{0,0,\#},B_{1,0,\#},B_{1,0,\#}$

Der Zustand von $T$ codieren wir mit:

$S_{0,S_0},S_{0,S_1},S_{1,S_0},S_{1,S_1}$

Für die Kopfposition haben wir sechs Variablen:

$P_{0,-1},P_{0,0},P_{0,1}$

$P_{1,-1},P_{1,0},P_{1,1},$

Mit diesen Variablen haben wir alle Variablen repräsentiert, die die Maschine $T$ einnehmen kann. Wenn wir die Maschine also in $SAT$ abbilden wollen, sieht die Formel $F$ dann so aus:

$F=S\wedge R\wedge T\wedge A$

Was bedeutet es?

$S$: Startbedingung. Initiale Konfiguration von $T$. Die Maschine befindet sich in $s_0$, das Eingabewort $\omega$ ist auf dem Band, der Rest ist leer und der Kopf befindet sich auf Position $0$.

$R$: Randbedingungen, die $T$ zu jeder zeit erfüllen muss, d.h. $R=(R_1\wedge R_2\wedge R_3)$ Diese sind:

$R_1$: Maschine befindet sich zu jedem Zeitpunkt in nur einem Zustand

$R_2$: Der Schreib-Lese-Kopf befindet sich immer nur an einer Position.

$R_3$: Es befindet sich nur ein Symbol an jeder Bandstelle zu jedem Zeitpunkt.

$T$: Transitionsbedingungen. In dieser Teilformel werden die möglichen Konfigurationsübergänge codiert, d.h. $T=(T_1\wedge T_2\wedge T_3)$ Sie bestehen aus:

$T_1$: Maschine geht in Folgekonfiuration über.

$T_2$: Inaktive Maschine, terminiert.

$T_3$: Bandinhalt wird geändert.

$A$: Akzeptanzbedingung. Hier wird codiert, dass die $TM$ das Wort $\omega$ dann annimmt wenn es im Endzustand anhält. Der Zustand muss in weniger als $p(n)$ Berechnungsschritten erreicht werden.

Und nun kommt der Spaß an der Sache. Alle Bedingungen können wir als Formel codieren.

Beispiel: nehmen wir an, das Wort $\omega$ besteht aus $\#$, d.h. auf dem Band steht $B\# B$. Die oben in Prosa verfasste Startbedingung, wäre dann:

$S=S_{0,s_0}\wedge{P_{0,0}}\wedge{B_{0,-1,B}}\wedge{B_{0,0,\#}}\wedge{B_{0,1,B}}$

In Worten ausgedrückt: Die Maschine befindet sich nach $0$ Schritten im Zustand $s_0$ (erste Bedingung), der Lesekopf nach $0$ Schritten auf Position $0$ (zweite Bedingung) und auf dem Band steht auf Positionen $-1,0,1$ eben $B,\#,B$ (dritte, vierte und fünfte Bedingung). Und wenn das alles stimmt, die Variablen also alle mit einer $1$ belegt sind, dann evaluiert die Formel $S$ bei Auswertung zu $1$. Oh mein Gott! Das ist genau das, was wir für die Maschine $T$ festgelegt und nun in eine Formel gequetscht haben.

Haben wir z.B. ein leeres Wort $\epsilon$, d.h. auf dem Band steht $BBB$, so sieht unsere Startbedingung wie folgt aus:

$S=S_{0,s_0}\wedge{P_{0,0}}\wedge{B_{0,-1,B}}\wedge{B_{0,0,B}}\wedge{B_{0,1,B}}$

Gleiches gilt für Rand-, Transitions- und Akzeptanzbedingungen, die wir eben auch als Formel darstellen können. Ist nur alles ziemliche Schreibarbeit. Wenn die alle erfüllt sind, evaluiert auch unsere Gesamtformel $F$ (siehe oben) zu einer $1$. Eventuell schreibe ich die kompletten Rand- und Transitionsbedingungen bei Gelegenheit hier nochmal hin.

Wie wir also sehen können, können wir die Bedingungen für eine Maschine $T$ in eine Formel $F$ quetschen, die genau das tut, was wir wollen. Wir haben also gezeigt, wie eine $NTM$ $T$ polynomiell auf eine aussagenlogische Formel reduziert werden kann, die genau dann erfüllbar ist, wenn $T$ in einem Endzustand terminiert.

Ein ausführlicher Beweis ist z.B. auch hier zu finden.

Hier entfaltet $SAT$ seinen Charme: wir können viele Algorithmen auf $SAT$ zurückführen, indem wir den Ablauf in die Formel hineincodieren und damit das Problem auf $SAT$ reduzieren. Und was passt hier besser als Beispiel, als $3SAT$?

Antwort zum Lernziel: wir codieren eine komplette Aussagenlogische Formel in ein Wort für eine Turingmaschine, deren Laufzeit polynomiell beschränkt ist. Die Maschine terminiert nur wenn die aussagenlogische Formel wahr ist. Es ist leicht einzusehen, dass diese initiale Turingmaschine, also praktisch unser $NP$-vollständiges Problem (wo leicht einzusehen ist, dass es tatsächlich in $NP$ liegt), in polynomzeit durch eine Kontroll-Turingmaschine entschieden werden kann.

In die Eingabe dieser Maschine dieses wird dann die zu prüfende, aussagenlogische $SAT$-Formel codiert und von dieser $KTM$ ebenfalls in Polynomzeit entschieden.

Lernziel 4

Wie führt man eine einfache, polynomielle Reduktion ${}\leq_{pol}$  aus?

Reduktion von $SAT$ auf $3SAT$

Die Frage bei $3SAT$ ist:

Gibt es eine erfüllende Bedingung bei $n$ aussagenlogischen Klauseln mit maximal $3$ Literalen (atomare Aussage, z.B. $\neg{A}$ oder $A$)?

Damit ist $3SAT$ eine abgeschwächte Form von $SAT$. Einschränkung ist, dass die Formel für $3SAT$ in der Konjunktivform (mit $\wedge$ verknüpft) vorhanden sein muss. Um also zu zeigen, dass $3SAT$ ebenfalls $NP$-hart ist, müssen wir $SAT$ auf $3SAT$ polynomiell reduzieren, formal ausgedrückt:

$SAT\leq_{pol}3SAT$

Was wir tun müssen, ist also eine allgemeine Formel nehmen und sie so umformen, dass die beliebig viele Klauseln, aber nur drei Literale pro Klausel hat. Das machen wir mit Hilfe von Hilfsvariablen. Haben wir also ein Term in der folgenden Form in KNF mit $n$ Variablen:

$(\upsilon_{1,1}\vee\upsilon_{1,2}\vee ...\vee\upsilon_{1,n})\wedge(\upsilon_{m,1}\vee\upsilon_{m,2}...\vee\upsilon_{m,n_{m}})$

Für jede Klausel mit $n$ Variablen entstehen $n-2$ neue Klauseln mit $n-3$ neuen Variablen:

$(\upsilon_{1,1}\vee\upsilon_{1,2}\vee a_{1,1})\wedge(\overline{a_{1,1}}\vee\upsilon_{1,3}\vee a_{1,2})\wedge ...\wedge(\overline{a_{1,n-3}}\vee \epsilon_{1,n_{1}-1}\vee\epsilon_{1,n_{1}})$

Hilfsvariablen? Ja, Hilfsvariablen. Diese Variablen zeigen uns an, welcher Teil aus der zerteilen Klausel das ganze Konstrukt hat wahr werden lassen.

Beispiel? Klar: $(A\vee\overline{B}\vee C\vee\overline{D})\wedge(E\vee F\vee G)$

Die erste Klausel wandeln wir also um in $2$ Klauseln mit einer neuen Variable. Die zweite Klauseln können wir so lassen, da wir da bereits drei Literale drin haben. Nennen wir unsere neue Hilfsvariable also einfach $h_1$. Damit sehen unsere beiden neuen Klauseln nun so aus:

$(A\vee\overline{B}\vee h_1)\wedge(C\vee\overline{D}\vee\overline{h_1})$

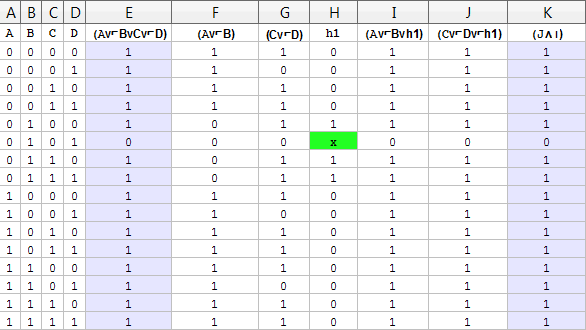
Der Trick hierbei ist, dass die Hilfsvariable $h_1$ dann falsch wird, wenn die erste Teilklausel wahr wird und wahr wird wenn die zweite Teilklausel wahr wird. Stellen wir doch eine kleine Wertetabelle für den umgeformten Term zusammen, wie wir das auch in der technischen Informatik (Computersysteme 1&2) gemacht haben:

Ich habe Excel etwas vergewaltigt, nehmt mir das nicht übel. Die Spalten haben folgende Bedeutung:

• In den Spalten A-D stehen alle unsere Variablenbelegungen $A,B,C,D$.
• In Spalte E steht die umzuformende Klausel $(A\vee\overline{B}\vee C\vee\overline{D})$.
• In Spalte F steht die so entstandene erste Teiltklausel,
• In G die zweite.
• In Spalte H steht unsere Hilfsvariable $h_1$, die falsch wird wenn die erste Teilklausel in Spalte F wahr ist und wahr wird wenn die zweite Teilklausel in Spalte G wahr wird. Der Inhalt von $h_1$ spielt keine Rolle wenn die Klausel sowieso negativ werden würde (grünes Kästchen).
• In Spalte I und J stehen unsere neuen Teilklausen mit der Hilfsvariable, die wir dann verwenden um die alte Klausel zu repräsentieren.
• Spalte K beherbergt dann beide Klauseln aus I und J mit einem $\wedge$ verknüpft. Genau diese Klausel
• in Spalte K ist dann: $((A\vee\overline{B}\vee h_1)\wedge(C\vee\overline{D}\vee\overline{h_1})$

Und sie tut genau das gleiche wie die initiale Klausel aus den vier Literalen, die wir umformen wollten: $(A\vee\overline{B}\vee C\vee\overline{D})$. Lange Rede, kurzer Sinn:

$(A\vee\overline{B}\vee C\vee\overline{D})$ $\Leftrightarrow$ $((A\vee\overline{B}\vee h_1)\wedge(C\vee\overline{D}\vee\overline{h_1})$

Klauseln mit nur einem Literal bekommen zwei Hilfsvariablen, Klauseln mit zwei Literalen eine, Klauseln mit drei Literalen werden nicht angefasst und Klauseln mit mehr als drei Literalen werden nach dieser Vorgehensweise rekursiv in Klauseln mit drei Literalen umgewandelt. Die Anzahl der Literale hat sich also nur linear erhöht und wir haben einen Weg gefunden $SAT$ auf $3SAT$ in Polynomzeit zu reduzieren. Nun können wir auch $3SAT$ für andere Schweinereien benutzen!

Antwort zum Lernziel: am beispiel von $3SAT$ sehen wir die Reduktion, indem wir eine aussagenlogische Formel so umformen, dass wir zwar beliebig viele Klauseln, aber nur drei Literale pro Klausel haben. Schaffen wir diese Reduktion in Polynomzeit durchzuführen, so ist sie uns gelungen.

Lernziel 5

Angabe einiger NP-vollständigen Probleme

Im Skript werden noch weitere Probleme besprochen, die $NP$-vollständig sind. Zwei davon sind $CLIQUE$ und $IND\_SET$. Fangen wir doch zunächst mit $CLIQUE$ an. Definition (erneut geklaut aus dem Buch von Hr. Hoffmann):

Graph $G$ mit Knotenmenge $V$ und Kantenmente $E$

Fragestellung: Existieren $n$ Knoten $v_1,...,v_n$, die paarweise durch eine Kante aus $E$ verbunden sind?

Menge $C=\{v_1,...,v_n\}$ mit dieser Eigenschaft heißt $CLIQUE$ der Größe $n$

In klaren Worten ist eine $CLIQUE$ eine Menge von Knoten, die alle miteinander verbunden sind.

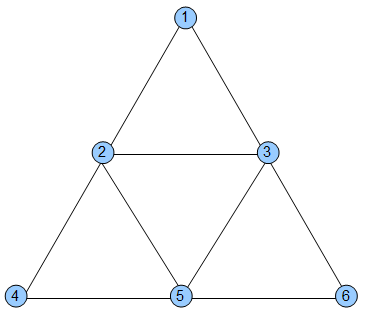
Beispiel: $G_1$ mit

$V_1=\{1,2,3,4,5,6\}$ und

$E=\{\{1,2\},\{1,3\},\{2,3\},\{2,4\},\{2,5\},\{4,5\},\{5,6\},\{6,3\},...\}$ (die Kanten in die andere Richtung habe ich aus Faulheit ausgelassen, denkt sie euch einfach dazu)

Hier haben wir Cliquen mit den Knoten $\{1,2,3\},\{2,4,5\},\{2,3,5\},\{3,5,6\}$ identifiziert. Um zu beweisen, dass wir eine Clique der Größe $n$ gefunden haben, müssen wir nur eine geeignete Knotenmenge raten und prüfen ob paarweise durch eine Kante verbunden sind. Raten wir z.B. $C=\{1,5,6\}$, müssen wir auf folgende Kanten prüfen: $\{1,5\},\{1,6\},\{5,1\},\{5,6\},\{6,1\},\{6,5\}$. Jaja, ungerichteter Graph, ich weiß: ein vorhandener Weg von $A$ nach $B$ impliziert den Weg von $B$ nach $A$. Aber wir tun uns mit der Prüfung aller Möglichkeiten nicht weh, da dieser sowieso polynomiell beschränkt bleibt. So können wir aber auch ungerichtete Graphen in die Betrachtung mit einbeziehen.

Liegen die Kanten also in unserer Menge $E$, so haben wir eine Clique gefunden. Man sieht leicht, dass mit der zu suchenden Cliquen-Größe der Aufwand, d.h. die Anzahl der zu prüfenden Kanten, quadratisch ($n^2$) in Abhängigkeit von $n$ zunimmt. Da wir eine Lösung raten und sie mit quadratischem Aufwand prüfen können, liegt unsere $CLIQUE\in NP$ .

Jetzt kümmern wir uns um den aufwendigeren Teil, die $NP$-Härte von $CLIQUE$. Dazu reduzieren wir einfach $3SAT$ auf $CLIQUE$. Wir müssen also eine Formel $M$ konstruieren, dass gilt:

$M$ ist erfüllbar $\Leftrightarrow G$ enthält eine Clique der Größe $n$

Achtung: wir verfolgen den Weg von einer Formel zum Graphen und nicht anders herum. Wir überführen also eine Formel, die wahr wird wenn sie eine Belegung hat in einen Graphen, der genau bei dieser Belegung eine Clique hat. Machen wir das am besten an einem Beispiel:

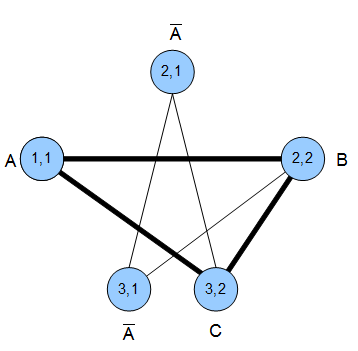
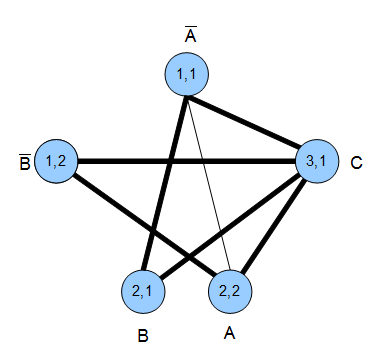
Beispiel: $(A)\vee(\neg{A}\wedge{B})\vee(\neg{A}\wedge{C})$

Wie basteln wir uns daraus einen Graphen? Nach folgenden Regeln:

• Jedes Literal wird ein Knoten
• Zwischen jedem Knoten gibt es eine Kante wenn
  • sie nicht in der selben Klausel stehen und
  • wenn sie gleichzeitig erfüllbar sind ($A$ und $\neg{A}$ sind z.B. nicht gleichzeitig erfüllbar)

Ganz einfach. Um es deutlicher zu machen, beschriften wir die Knoten mit $i,j$. $i$ ist die Nr. der Klausel und $j$ die Nummer des Literals in der Klausel. Z.B. wäre der Knoten, der das Literal $A$ in der ersten Klausel beschreibt, beschriftet mit $(1,1)$.

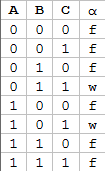
Mit den Knoten können wir auch direkt eine Belegung für die Formel ableiten, die sie wahr werden lässt: $A=B=C=1$. Wäre ein Knoten negativ, so würden wir das Literal ${}=0$ setzen. Probiert es mal selbst an der folgenden Wertetabelle aus und bastelt euch eine Formel und den dazugehörigen Graphen

Übung:

Lösung zeigen

Viele fragen sich auch, wie man eine Reduktion von $CLIQUE$ zu $3SAT$ erreichen kann, also genau der umgekehrte Weg weil es irgendwie natürlicher erscheint einen Graphen in eine Formel statt eine Formel in einen Graphen zu stecken. Es sei gesagt, dass es natürlich geht. Jedes Problem, dass $NP$-Vollständig ist, lässt sich polynomiell in ein anderes, $NP$-vollständiges Problem überführen. Jedoch evtl. nicht direkt. Der Weg von $CLIQUE$ zu $3SAT$ ist kein direkter, sondern führt über Teilgraph-Isomorphismus nach $SAT$, $3SAT$ und schließlich auf Vertex Cover, was wiederum auf $CLIQUE$ zurückgeführt werden kann. Ein Weg dazu wurde von Larcheri Paolo hier beschrieben.

Ein weiteres Problem, dass im Skript angesprochen wurde war $IND\_SET$. Damit beschreibt man die Frage ob es in einem Graphen eine Menge unabhängiger Knoten gibt. Die Suche nach der maximalen Anzahl ist $NP$-Vollständig. Da $CLIQUE$ und $IND\_SET$ sehr nah verwand sind (ein unabhängiges Set ist im Komplementgraph eines Graphen eine Clique) kann man beide aufeinander reduzieren. Ich spare mir hier die Reduktion (erstmal), Details könnt Ihr z.B. hier, hier oder hier nachlesen.

Weitere $NP$-vollständige Probleme sind z.B.

• Hamilonkreis (siehe Beitrag zu KE3)
• Traveling Salesman
• Vier-Farben-Problem
• Rucksack
• Partition
• ...

Im Skript wird auch über Optimierungsprobleme gesprochen. Ein klassischer Vertreter davon ist das Scheduling: die Verteilung von Prozessen mit entsprechenden Ausführungszeiten auf eine bestimmte Anzahl von Prozessoren, so dass die Gesamtzeit minimal ist. Vielen $NP$-vollständige Problemen kann man ein Optimierungsproblem zuordnen, was deren Bedeutung für die Informatik unterstreicht.

Da sie alle $NP$-hart sind und sich für große Eingaben eben einer effizienten Lösung entziehen, muss man nach sog. Approximationsalgorithmen ausschau halten, die sich einem optimalen Ergebnis möglichst nah annähren. Ein schlecht approximierbares Problem ist das angesprochene $CLIQUE$ (das Verhältnis zwischen der größten Clique im Graphen und der größten gefundenen Clique lässt sich nicht durch eine Konstante beschreiben), während das Rucksackproblem mit dem Greedy-Algorithmus sehr nah an einer guten Lösung sein kann.

Antwort zum Lernziel: einige $NP$-vollständige Probleme sind Hamilton, CLIQUE, Traveling Salesman, Rucksack und Partition. Weitere Probleme finden sich z.B. hier.

Lernziel 6

Warum ist $GAP$ vollständig für $NLOGSPACE$?

Letztes Lernziel! Also, was ist $GAP$? Es ist ein einfaches Erreichbarkeitsproblem in einem Graphen. Gibt es einen Weg von Knoten $a$ zu Knoten $b$? Die Tiefen- und Breitensuche löst das Problem in Polynomzeit. Für den Platzbedarf sind wir aber bei $O(\#V)$ (d.h. der Platzbedarf entspricht der Anzahl der Knoten), ein Algorithmus, der nur logarithmischen Platz beansprucht, ist nicht bekannt.

Eine $NTM$ kann das Problem jedoch mit der Bandschranke $O(log)$ erkennen. Die Achillesferse dabei ist: der Algorithmus ist gedächnislos. Besuchte Knoten und Wege werden vergessen, wir haben evtl. das Problem von Zyklen. Entschärft wird das durch die von uns gegebene Schranke: der Knotenanzahl im Graphen. Der Algorithmus bricht ab wenn die maximale Anzahl der Knoten ($\#V$) besucht wurde.

Der Beweis im Skript zeigt einen sehr engen Zusammenhang zwischen $NLOGSPACE$ und $GAP$:

Also warum beansprucht $GAP$ tatsächlich nur logarithmischen Platzverbrauch wenn er von einer $NTM$ erkannt wird (hier bitte Vorsicht, nutzen wir eine normale $TM$, müssen wir alle Knoten durchprobieren und dürfen uns mit $O(\#V)$ begnügen)? Der beschriebene Algorithmus arbeiten in etwa wie folgt ($a$ ist Start- und $b$ ist Endknoten):

1. $c:=a;i=\#V$ (setze Startknoten und maximale Knotenanzahl als längster Weg gesetzt)
2. Wenn $c=b$, akzeptiere, ansonsten Schritt 3 (wenn Endknoten erreicht).
3. rate neuen Knoten $d$. Setze $i:=i-1$, Schritt 4 (neuer Knoten aus Graph wird geraten und ein Schritt vom Weg abgezogen).
4. Wenn $i=0$ oder $(c,d)\notin E$, verwerfen und nochmal neu raten: Schritt 3. Sonst Schritt 5 (wenn maximale Anzahl an Knoten besucht wurde, d.h. der längste Weg beschritten, ist der Weg mist. Gleiches gilt wenn ein Folgeknoten $d$ geraten wurde, und es zu diesem keine Kante/keinen direkten Weg gibt).
5. $c = d$, Schritt 2 (es gibt also einen direkten Weg von $c$ nach $d$, d.h. das wird unser nächster Knoten von dem wir losgehen).

Alle Knoten und Zahlen (insg. 5) werden als Dualzahlen gespeichert und wir verbrauchen damit weniger Speicherplatz als die anderen Algorithmen mit $O(\#V)$. Da der Algorithmus gedächnislos ist, speichern wir auch keine Adjazenzmatrix und auch nicht den Weg. Raten wir also in Schritt 3 mehrmals ziemlich blöd, so laufen wir ggf. die ganze Zeit im Kreis. Wir fragen aber nicht nach dem kürzesten Weg, sondern ob es überhaupt einen gibt.

Damit ist zunächst $GAP\in NLOGSPACE$. Nun müssen wir eine Reduktion $L\leq_{log}GAP$ zeigen. Dazu wird eine Maschine mit Bandschranke $O(log)$ erstellt, die $L$ entscheidet und die Eingabe der Maschine als Graph codiert. Die Knoten sind alle Konfigurationen der Maschine bei der Eingabe von $x$. Gibt es bei der Eingabe von $x$ von einem Zustand ausgehend einen Folgezustand, so ist das eine Kante im Graphen. Führt $x$ also zu einer Endkonfiguration, so gibt es auch einen Weg in diesem Graphen von $x$ zum Endzustand. Damit sind wir mit der Reduktion auch schon durch.

Achtung: die Reduktionen $\leq_{pol}$ beziehen sich immer auf Zeit. Polynomialplatz ist zu mächtig für Reduktionen. Während $\leq_{log}$ sich immer auf Platz bezieht, da wir zeitlich nicht einmal die Eingabe hätten lesen können bei dieser Reduktion.

Antwort zum Lernziel: das Erreichbarkeitsproblem wird mit logarithmischem Platzverbrauch mit einer $NTM$ entschieden weil der Algorithmus gedächnislos ist. Es können also Zyklen entstehen, die wir nicht erkennen können. Der maximale Platzverbrauch ist jedoch die maximale Anzahl an Knoten weil der Algorithmus abbricht wenn die Anzahl der besuchten Knoten der Anzahl der Knoten im Graph entspricht. Da wir aber nicht nach dem kürzesten Weg fragen, sondern nur ob es einen gibt reicht uns das aus.

Die Reduktion der Eingabe auf eine Maschine mit Bandschranke $O(log)$ erfolgt wie oben beschrieben.

Wieder: wer Fehler findet, bitte ab damit in die Kommentare oder eine Mail an mich.

Datum: 20. Mai 2013
Kategorie: Theoretische Informatik
Kommentarfeed: RSS 2.0 • Trackback: Trackback-Url

Sie können zum Ende springen und ein Kommentar hinterlassen. Pingen ist im Augenblick nicht erlaubt.