TIB: Nichtsdeterministische Komplexität (Lernziele KE3, Update 3)

Update: durch den Hinweis von Philipp ist mir noch etwas aufgefallen. Der Vergleich von deterministischen Turingmaschinen zu nichtdeterministischen ist nicht ganz deutlich rüber gekommen. Daher habe ich den Abschnitt noch einmal überarbeitet (Lernziel 2, 3 und 4).

Update: Antworten zu den Lernzielen.

Das ist ein schönes Thema. Wirklich. Auch keinerlei Sarkasmus hier drin versteckt. Ich möchte - wie im Skript auch - zunächst den Nichtdeterminismus anhand eines klassischen Problems erläutern:

Hamiltonkreisproblem

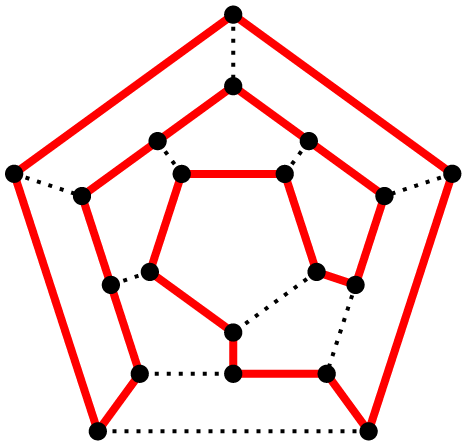
Zunächst: was ist ein Hamiltonkreis? Ein Hamiltonkreis ist ein Weg in einem Graphen, der jeden Knoten genau 1x enthält. Es ist ein Problem aus der Graphentheorie. Ich klaue mir wieder ein Bild aus der zugehörigen Wikipedia-Seite um das zu verdeutlichen:

Quelle: Wikipedia 

Das Problem ist es diesen Weg in so einem Graphen zu finden (sinniger Weise ist einer schon im Bild eingezeichnet). Problem? Wir könnten alle Wege durchprobieren. Jeden Knoten mal durchtesten. Das Problem hierbei ist jedoch, dass der Aufwand exponentiell ist (in Abhängigkeit von der Anzahl der Knoten). Was wir brauchen ist jedoch ein effizienter Algorithmus.

Hier kommt unser Nichtdeterminismus ins Spiel, denn uns interessieren ja vielleicht nicht alle Hamiltonkreise im Graphen, sondern einfach nur ob es einen gibt. Was wäre dann der Ansatz? Raten und Prüfen! Wir raten eine Knotenfolge und prüfen ob sie uns in einem Hamiltonkreis bringt. Und das geht in Polynomialzeit mittels einer nichtdeterministischen TM, einer $NTM$.

Lernziel 1

Erklärung der Modelle der KTM und der NTM

Die Kontrollturingmaschine (KTM) aus dem Skript tut nichts weiter als das zu prüfen. Es bekommt zwei Eingaben, nämlich $x$ (auf dem Eingabeband) und $y$ (auf Band 0, was als Ausgabeband ausgezeichnet ist, aber nicht benötigt wird), wobei $y$ ein Beweis dafür sein soll, dass $x\in{L}$. Hält die Maschine also in dem ausgezeichneten Endzustand $q_{+}$, so ist $y$ ein Beweis, dass $x\in{L}$. Wir müssen hier aber jedes Mal das $y$ (z.B. die zu testende Knotensequenz) auf Band 0 schreiben.

Wir können das $y$ aber auch raten lassen. Hierfür ist unsere nichtdeterministische Turingmaschine (NTM) da. Statt einer Übergangsfunktion (bei einem entsprechenden Zustand und einem entsprechenden Zeichen unter dem Lesekopf wird spezifiziert was unter den Lesekopf geschrieben, in welche Richtung sich bewegt und welcher Zustand als nächstes eingenommen werden soll) wird hier eine Übergangsrelation (es gibt mehrere Übergänge, die zufällig ausgeführt werden) verwendet. Jetzt zieht Ihr die Augenbrauen zusammen, richtig? Das liegt daran, dass dieses Modell kein Modell ist, welches man real implementieren kann: es ist rein theoretischer Natur. Löst euch also etwas von eurer "Hardware" 😉 Wenn man also irgendwelche Abzweigungen nimmt und am Ende in einem der Endzustände landet, so ist $x\in{L}$. Es zählt also einfach nur, dass es einen Weg, der die Maschine in einen Endzustand führt gibt wenn $x\in{L}$ ist.

Durch die Verzweigungen bilden die Berechnungen am Ende einen Baum, dessen Rechenzeit $t_M$ die Tiefe des Baums darstellt. Der Bandbedarf $s_M$ ist das Maximum des Bandbedarfs aller Knoten in diesem Baum.

Antwort zum Lernziel: mit der Kontrolltunringmaschine (KTM) prüfen wir eine vorgegebene Lösung auf ihre Richtigkeit. Die vorgegebene Lösung wird Hilfseingabe genannt und muss immer manuell eingegeben werden.

Mittels nichtdeterministischer Turingmaschine (NTM) können wir diese Hilfseingabe auch raten lassen: dabei bekommt die NTM eine Übergangsrelation, die nicht eindeutig ist. Bei einer Belegung und einem Zustand kann kann es also mehrere Folgezustände geben, so dass eine zufällige Auswahl erfolgt (oder alle möglichen Pfade parallel durchlaufen werden).

Lernziel 2

Äquivalenz der Modelle begründen

Spannend ist, dass beide Modelle (KTM und NTM) äquivalent sind. Vor allem, dass man sie gegenseitig innerhalb der gleichen Zeit- und Bandschranken ineinander überführen kann. Die Überführung einer KTM in eine NTM geschieht zunächst wie folgt:

KTM nach neue KTM mit Hilfsalphabet $\{0,1\}$

 1. die KTM wird in eine neue KTM mit dem Alphabet $\{0,1\}^m$ überführt ($2^m$ wenn die Anzahl der Zeichen nicht bereits eine Zweierpotenz darstellt)

2. die Befehle der alten KTM werden durch Befehlsfolgen ersetzt, wo der Befehl $m$ aufgerufen wird. Ebenso ergeht es den Tests

Die Laufzeit erhöht sich hier nur um einen konstanten Faktor. Und da dieser uns bei der Betrachtung der Schranke nicht interessiert, bleiben wir innerhalb der Laufzeit der alten KTM. Ebenso beim Bandbedarf.

Neue KTM nach NTM

Nun erzeugen wir aus der neuen KTM mit Hilfsalphabet $\{0,1\}$ eine NTM. Das Problem hierbei: wir müssen $y$, die Eingabe, nun erzeugen und kennen ihre Schranke nicht. Dazu wird auf dem Arbeitsband $k+2$ ($k$ ist die Anzahl der Arbeitsbänder der neuen KTM) die Kontrolleingabe $y$ während der Simulation der neuen KTM erzeugt. Jeder Schritt der neuen KTM wird durch maximal 4 Schritte simuliert und der Bandbedarf vergrößert sich um 1. Alles konstante Faktoren und unwichtig.

NTM zur alten KTM

Um den Bogen wieder zurück zu schlagen müssen alle Verzweigungen durch einen Test auf dem Eingabeband 0 ersetzt werden.

Antwort zum Lernziel: Die Äquivalenz von Kontrollturingmaschinen und nichtdeterministischen Turingmaschinen begründet sich darin, dass man beide ineinander überführen kann und die Simulation innerhalb der gleichen Band- und Zeitschranken geschieht (wenn man von den konstanten Faktoren mal absieht).

Achtung: Bitte verwechselt nicht KTMs und DTMs. Nichtdeterministische Turingmaschinen (NTMs) sind zwar ebenfalls äquivalent zu deterministischen Turingmaschinen (DTMs), da man NTMs in DTMs überführen kann. Aber das geschieht nicht innerhalb der gleichen Zeit- und Bandschranken!

Nach dem Satz von Savich gilt, dass wenn eine NTM ein Problem polynomiell lösen kann, kann eine äquivalente DTM das Problem in exponentieller Zeit lösen. Der Speicherplatzbedarf erhöht sich ebenfalls: er wird quadratisch.

Exkurs: Hamiltonkreisproblem in der KTM

Um z.B. das Hamiltonkreisproblem in einer KTM zu entscheiden, müssen wir das Problem formalisieren. Dazu wird der Graph als Adjazenzmatrix geschrieben und zeilenweise aufgeschrieben. Als Kontrolleingabe dient dann eine Folge von Knoten und die KTM prüft die Eingabe auf die gesuchte Eigenschaft.

Lernziel 3

Definition nichtdeterministischer Komplixitätsmaße und -klassen

Da wir KTMs durch NTMs mit den gleichen Schranken simulieren können gilt:

$ZEIT(f)\subseteq NZEIT(f)$

$BAND(f)\subseteq NBAND(f)$

sowie

$NZEIT(f)\subseteq BAND(f)$

Definieren wir hier auch $NZEIT(f)$:

$NZEIT(f)\subseteq\bigcup_{c\in\mathbb{N}}ZEIT(c^{f(n)})$

Mit der Menge $NZEIT$ geben wir die Menge der Sprachen an, die von einer nichtdeterministischen Turingmaschine in Zeit $O(f)$ akzeptiert werden können (Wikipedia).

Die Reihenfolge darf hier auch nicht fehlen: $P\subseteq NP\subseteq PSPACE\subseteq\bigcup_{c\in\mathbb{N}}ZEIT(2^{n^{c}})$

Ebenso der nichtdeterministische Bandbedarf:

Sei $log\in O(f)$, so gilt:

$NBAND(f)\subseteq\bigcup_{c\in\mathbb{N}}ZEIT(c^{f(n)})$ und $LOGSPACE\subseteq P$.

Sowie

$NBAND(f)\subseteq BAND(f(n)^2)$ und $NPSPACE = PSPACE$ (Satz von Savitch)

Wichtig: noch ein paar Ergänzungen zum Satz von Savitch: dieser Satz besagt nichts anderes, als dass jedes von einer $NTM$ (nichtdeterministisch, d.h. wir orakeln die Lösungseingabe) lösbares Problem  auch von einer $DTM$ (deterministisch, d.h. wir orakeln nicht) in exponentieller Zeit gelöst werden kann und der Platzbedarf dieser Maschine nur quadratisch höher liegt. Die Folgerung aus diesem Satz bedeutet, dass die Bandkomplexitätsklasse $NPSPACE$ mit der Bandkomplexitätsklasse $PSPACE$ übereinstimmt.

Antwort zum Lernziel: Definitionen siehe oben.

PS: Wie im vorherigen Lernziel angedeutet: verwechselt bitte nicht NTMs/KTMs/DTMs. Und merkt euch den Satz von Savitch 😉

Lernziel 4

Zusammenhang zwischen deterministischen und nichtdeterministischen Komplexitätsklassen

Antwort zum Lernziel: durch die Überführung der nichtdeterministischen Turingmaschinen in deterministische Kontrollturingmaschinen, die die selben Komplexitätsklassen in Zeit und Band inne haben besteht hier ein entsprechend enger Zusammenhang.

Update: Ebenso verhält es sich bei der Überführung von nichtdeterministischen Turingmaschinen in deterministische Turingmaschinen. Nach Savitch haben diese aber nicht die gleichen Zeit- und Bandschranken.

Nach dem Satz von Savich gilt, dass wenn eine NTM ein Problem polynomiell lösen kann, kann eine äquivalente DTM das Problem in exponentieller Zeit lösen. Der Speicherplatzbedarf erhöht sich ebenfalls: er wird quadratisch.

Lernziel 5

Definition von ${}\leq_{pol}{}$

Hierzu bemühen wir noch einmal unsere Definition der Reduzierbarkeit: wenn wir Mengen auf andere Mengen reduzieren könne, so gelten die Eigenschaften der kleineren Menge auch für dir größere. Der Unterschied zu dem Verfahren in der Komplexitätstheorie ist es, dass wir nun Wortfunktionen statt Zahlenfunktionen verwenden und diese Überführungsfunktionen nur aus einer bestimmten Komplexitätsklasse für Funktionen zulassen. Es eignen sich nur Komplexitätsklassen, die unter Komposition (wenn sie $f,g$ enthalten, enthalten sie auch $f\circ g$) abgeschlossen sind. Kämpfen wir uns also durch die Definition:

LOGSPACE und polynomielle Reduzierbarkeit

$L$ heißt $LOGSPACE$-reduzierbar auf $M$ ($L\leq_{log}{}$) wenn es eine Funktion $f$ aus der Klasse $FLOGSPACE$ gibt und für alle $x\in L$ gilt, dass $f(x)\in M$ ist.

$L$ heißt polynomiell-reduzierbar auf $M$ ($L\leq_{pol}{}$) wenn es eine Funktion $f$ aus der Klasse $FP$ gibt und für alle $x\in L$ gilt, dass $f(x)\in M$ ist.

Die Überführungsfunktion muss für die $LOGSPACE$-Reduzierbarkeit also aus der logarithmischen Komplexitätsklasse stammen, während für die polynomielle Reduzierbarkeit gefordert wird, dass die Funktion aus der polynomiellen Komplexitätsklasse kommen muss. Damit haben wir den zentralen Satz für unsere Komplexitätsklassen:

LOGSPACE, NLOGSPACE, P, NP, PSPACE sind abgeschlossen gegen $\leq_{log}{}$, P, NP, PSPACE aber auch gegen $\leq_{pol}{}$

Die meisten von euch werden das "F" vor *SPACE schon korrekt gedeutet haben. Da ich aber selbst kurz drüber nachgedacht habe, es im Skript aber nur in einem Nebensatz gefallen ist, möchte ich noch einmal darauf hinweisen. Während wir in z.B. in LOGSPACE, P, ... Sprachen (die in der Zeit entschieden werden können) drin liegen haben, haben wir in FLOGSPACE, FP, ... aber Funktionen. Diesen Unterschied solltet Ihr im Kopf behalten (Danke Barbara).

Antwort zum Lernziel: Mit der polynomiellen Reduktion ist es uns möglich mit Angabe einer Funktion (die innerhalb der polynomiellen Komplexitätsklasse ist) eine Menge auf eine andere zu reduzieren und so Eigenschaften der Menge quasi zu "vererben". Das spielt eine wichtige Rolle bei dem Beweis der $NP$-Vollständigkeit von Mengen.

Lernziel 6

Erklärung der Vollständigkeit

Kümmern wir uns zunächst um die Definition aus dem Skript:

$M$ ist $NP$-hart wenn $L\in{NP}$, $L\leq_{pol}{M}$

Bedeutet: $M$ ist $NP$-hart wenn es eine Menge $L$ in $NP$ gibt, die wir auf die Menge $M$ in polynomieller Zeit reduzieren können. Haben wir also eine Menge $L$, die nachgewiesen $NP$-hart ist, und können wir mit einer polynomiellen Überführungsfunktion $f\in{FP}:L\rightarrow M$ (zu einem $x$ aus $L$ bekommen wir mit $f(x)=y$ ein $y$ aus $M$) diese Menge auf $M$ reduzieren, so ist die Menge $M$ eben $NP$-hart.

Noch einmal drüber nachdenken, was $NP$-hart bedeutet? Das Problem ist mit einer nichtdeterministischen Turingmaschine (NTM) in polynomieller Zeit lösbar. Das Problem ist dann $NP$-hart wenn sich alle nichtdeterministisch polynomiell lösbaren Probleme darauf reduzieren lassen (danke Barabara). Wie z.B. unser Hammiltonkreisproblem (das ist zudem auch noch $NP$-vollständig, aber dazu gleich mehr). Definition gemerkt und verstanden? Gut, dann weiter.

$M$ ist $NLOGSPACE$-hart wenn $L\in{NLOGSPACE}$, $L\leq_{log}{M}$

Das Selbe in Grün. Nur wird hier die logarithmische Reduzierbarkeit der Menge gefordert. Jetzt kommt das, warum es diesen Abschnitt überhaupt gibt. Die Vollständigkeit:

$M$ heißt $NP$-vollständig wenn: $M$ $NP$-hart und $M\in{NP}$

Wir sprechen hier also von Vollständigkeit wenn $M$ zu der Klasse $NP$ gehört (eine $DTM$ kann in polynomieller Zeit die Richtigkeit der geratenen Lösung verifizieren) und alle anderen Mengen aus $NP$ mittels einer Überführungsfunktion $f$ in polynomieller Zeit (d.h. $f\in{FP}$) auf die Menge $M$ überführt werden können. Ist ein langer Satz, lest ihn ein paar Mal langsam durch bis sich bei euch im Kopf ein Bild zeichnet. Damit sind alle $NP$-vollständigen Probleme auch $NP$-hart. Das gleiche gilt dann für $NLOGSPACE$ und $P$:

$M$ heißt $NLOGSPACE$-vollständig wenn: $M$ $NLOGSPACE$-hart und $M\in{NLOGSPACE}$

$M$ heißt $P$-vollständig wenn: $M$ $P$-hart und $M\in{P}$

Das war schon etwas entspannter als der vorherige Beitrag zu KE2, oder?

Antwort zum Lernziel: die Vollständigkeit einer Menge zu einer Komplexitätsklasse bedeutet nicht nur, dass die Menge mit einer Turingmaschine erkannt werden kann, deren Schranke innerhalb der Komplexitätsklasse liegt. Sondern auch, dass sich alle anderen, vollständigen Probleme aus dieser Komplexitätsklasse darauf reduzieren lassen. Alle Eigenschaften, die wir für eine Klassen-vollständige Menge darlegen gelten auch für alle anderen Klassen-vollständigen Mengen.

Der Vorteil bei vollständigen Problemen in einer Klasse ist, dass wenn wir es z.B. schaffen für ein $NP$-Vollständiges Problem einen polynomiellen Algorithmus anzugeben, der das Problem entscheidet, so haben wir gleichzeitig für alle $NP$-vollständigen Probleme einen Lösungsweg gefunden, da sich diese polynomiell aufeinander (wenn auch mit Zwischenschritten) reduzieren lassen.

Da wir noch bisschen Platz im Beitrag haben, würden sich vielleicht einige Details zum Begriff Vollständigkeit hier gut machen:

Rekapitulation: wozu ist die Vollständigkeit gut?

(dieser Abschnitt hat das rechts oben verlinkte Buch von Dirk. W. Hoffmann - absolute Kaufempfehlung - und diverse Internet-Artikel als Informationsbasis)

Die Vollständigkeit ist ein zentrales und wichtiges Werkzeug der theoretischen Informatik. Sie vereinfacht eine Dinge ungemein. Durch die Reduktion können wir alte Probleme auf neue reduzieren, d.h. wir vererben quasi Komplexitätsaussagen von einer Menge auf eine andere. Was ist hier also der Unterschied zwischen hart und vollständig? Ein Problem/eine Menge $M$ ist z.B. $NP$-hart wenn sich alle Probleme aus der Klasse $NP$ auf dieses reduzieren lassen. Die Menge $M$ selbst muss nicht in $NP$ liegen. Erst wenn die Menge selbst in $NP$ liegt, spricht man von Vollständigkeit.

Wie zeigen wir Vollständigkeit?

1. Zunächst müssen wir zeigen, dass ein z.B. Problem in der Klasse $NP$ liegt: Wir geben eine $NTM$ an (eine $DTM$ würde sogar auch reichen), die die Eingabe in polynomieller Zeit auf Richtigkeit prüft. haben wir das getan, so fehlt uns nur noch der Nachweis der Reduktion:
2. Nun zeigen wir die $NP$-Härte: dass mittels polynomieller Reduktion sich alle Mengen aus $NP$ auf unsere untersuchte Menge $M$ reduzieren lassen. Das machen wir, indem wir irgendeine Menge aus $NP$ nehmen, die selbst bereits als vollständig eingestuft wurde. Warum können wir das tun? Durch die Transivität der Überführungsfunktion.

Done. Ist kein vollständiges Problem für eine Klasse bekannt, so wird die generische Reduktion angewandt. Ein Beispiel hierzu gab Stephen A. Cook (der lebt noch) in seinem berühmten Satz (für den er auch den Turing-Award bekam). Er zeigte, dass das SAT-Problem $NP$-Vollständig ist. Fortan konnte man für andere Mengen mittels Reduktion von SAT auf diese die $NP$-Vollständigkeit einfach nach dem oben beschriebenen Verfahren gezeigt werden. Im nächsten Beitrag werden wir versuchen $SAT$ als $NP$-hart zu beweisen ohne die Abkürzung mittels Reduzierbarkeit zu nehmen.

Welche Vorteile hat die Vollständigkeit noch?

Einer der Vorteile der Vollständigkeit ist die Beziehung zu allen anderen vollständigen Problemen in der Komplexitätsklasse. Nehmen wir z.B. $NP$: gelingt es uns für ein $NP$-vollständiges Problem zu zeigen, dass es in polynomieller Zeit lösbar ist (schaffen wir z.B. das Hamiltonkreisproblem in deterministischer, polynomieller Zeit zu lösen), so sind auch direkt alle anderen vollständigen Probleme aus der Klasse $NP$ deterministisch polynomiell lösbar. Damit wäre die Beziehung $P=NP$ positiv bewiesen, was als eines der wichtigsten, mathematischen Probleme unserer Zeit gilt. Aus diesem Grund wurde es auch in die Liste der Millenium-Probleme aufgenommen. Neben Ruhm und Ehre gibt es oben drauf noch eine Million USD vom Clay Mathematics Institute.

Damit sind wir auch mit der Kurseinheit 3 durch.

Auch wenn ich mich mittlerweile wie eine Schallplatte anhöre: wer Erklärungs-Fehler findet, bitte ASAP melden damit ich das sofort korrigieren kann.

Buchempfehlung

Datum: 4. Mai 2013
Kategorie: Theoretische Informatik
Kommentarfeed: RSS 2.0 • Trackback: Trackback-Url