TIB: NP-Vollständige Probleme (Lernziele KE4 1/2, Update 2)

Update: Antworten zu den Lernzielen hinzugefügt.

Nach dieser Kurseinheit haben wir mehr als die Hälfte des Weges geschafft und das Licht am Ende des Tunnels ist schon sichtbar. Hoffen wir, dass es kein Zug ist.

Die Grundlagen des Beweises der Vollständigkeit einer Menge haben wir bereits in diesem Beitrag skizziert. Dass der Beweis nicht unbedingt schwierig ist wenn bereits ein Problem als $NP$-vollständig bewiesen ist und wir eine Reduktion durchführen können, haben wir bereits gelernt. Schwieriger ist es jedoch die $NP$-Vollständigkeit ohne diese Reduktion von einer bereits bekannten Menge zu beweisen. Wir wenden uns in diesem Beitrag den zwei Problemen aus dem Skript zu und tun dies.

Lernziel 1

Wie ist der Vollständigkeitsbeweis zu 2D-DOMINO?

Bevor diese Frage beantworten: Was ist $2D-Domino$? Es wird auch als Kachelproblem bezeichnet. Unter diesem Namen findet sich auch in der Literatur eine Erklärung, wer mit der Beschreibung aus dem Skript nicht weiterkommt. Im Grunde geht es um die vollständige Belegung des Spielbretts nach bestimmten Regeln. Aber fangen wir erstmal klein an und zerlegen die Definition aus dem Skript:

$N\in\mathbb{N}$

Das ist die Größe des quadratischen Brettes. Ist $N := 4$, so ist unser Spielbrett $4x4$ Felder groß.

$S\subseteq{({\{0,1\}}^{+})}^4$

Damit bezeichnen wir den Satz unserer Spielsteine. Ein Spielstein ist gegeben durch ein Quintupel: $(L,R,O,U)\in{({\{0,1\}}^{+})}^4$. Nehmen wir an, dass wir z.B. $S=\{\{0,0,0,0\},\{0,0,0,1\}\}$ als Steinsatz haben, so befinden sich in unserem Satz zwei Steine: einer hat gar keine Markierung und einer nur unten (siehe nächste Abbildung).

Update: Barbara hat mich hier auf etwas hingewiesen. $(L,R,O,U)\in{({\{0,1\}}^{+})}^4$ bedeutet, dass wir $L,R,O,U$ als Worte über ${\{0,1\}}^{+}$ codieren können. D.h. wir können z.B. auch einen einzelnen Stein mit $\{1011,1111,1000,0001\}$ abbilden. Die einzelnen Elemente für $L,R,O,U$ bezeichnen dann die Farbe links, rechts, oben oder unten im Stein. Bei einem Wort mit der Länge $4$ haben wir somit $2^4=16$ verschiedene Farben, die wir nutzen können.

Bei $4$ Feldern auf dem Stein, die jeweils mit $16$ unterschiedlichen Farben codiert werden können, haben wir also $16^4=65536$ unterschiedliche Möglichkeiten einen Stein zu codieren.

Ich bin aber eine faule Sau und habe nur die Farben Schwarz und Weiß zugelassen um eine kleinere Menge an Steinen zu haben. Das habe ich nicht so konkret aufgeführt, wie ich das eig. gedacht habe. Dem Beispiel tut das aber keinen Abbruch. Daher schränke ich für mein Beispiel die Menge der Steine hier (im Gegensatz zum Skript, bitte daher also nicht vergessen: im Skript sind die Farben codiert mittels einem Wort über ${\{0,1\}}^{+}$) ein auf: $(L,R,O,U)\in({\{0,1\}}^{1})^4$

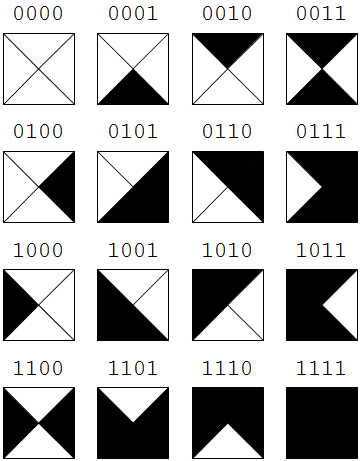
Die folgende Abbildung zeigt alle $2^4$ Möglichkeiten für die Belegung der Steine, d.h. wir haben insg. 16 Steine in unserer Menge $S$.

Kommen wir zur Anfangsbelegung:

$\alpha: \{1,...,N\}^2\rightarrow S\cup\{\varepsilon\}$

Mit $\alpha$ bezeichnen wir die Anfangsbelegung eines Feldes auf dem Brett. Hat unser $4x4$ Brett z.B. die ersten Beiden Felder mit einem vollständig weißen und einem vollständig schwarzen Stein belegt, während alle anderen leer sind, so wäre $\alpha(1,1) = (0,0,0,0)$, $\alpha(1,2) = (1,1,1,1)$ und der Rest der Felder ${}=\varepsilon$. Das alles kommt in unser $D$, d.h. als $D$ bezeichnen wir das gesamte Spiel mit: $D = (N,S,\alpha)$.

$\beta: \{1,...,N\}^2\rightarrow S$

Hier haben wir eine konkrete Belegung eines Feldes. Bitte beachten, dass die Belegung das leere Feld $\varepsilon$ nicht mehr mit einschließt. $D$ ist lösbar wenn wir die Anfangsbelegung auf dem Feld belassen und die restlichen leeren Felder nach folgenden Regeln belegen:

$(\beta(i,j) = (l,r,o,u)\land\beta(i,j+1) = (l^{'},r^{'},o^{'},u^{'}))\Rightarrow r=l^{'}$ und

$(\beta(i,j) = (l,r,o,u)\land\beta(i+1,j) = (l^{'},r^{'},o^{'},u^{'}))\Rightarrow u=o^{'}$

Kleiner Klopper. Sagt aber nichts anderes aus, als dass zwei Steine zueinander passen müssen. Der linke und rechte Stein müssen bei der jeweils zueinander liegenden Seite eine Markierung aufweisen. Das Gleiche gilt für den oberen und unteren Stein. Beispiel? Klar doch.

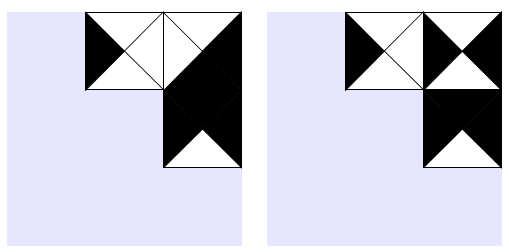
Wir sehen hier zwei Spielfelder mit $N=3$. Das 1. Spielfeld hat die Belegung:

$\beta(1,2) = (1,0,0,0)$, $\beta(1,3) = (0,1,0,1)$ und $\beta(2,3) = (1,1,1,0)$. Folgt daraus, dass $r=l^{'}$ und $u=o'$ wie oben angegeben? Versuchen wir es:

$(\beta(1,2) = (1,0,0,0)\land\beta(1,3) = (0,1,0,1))\Rightarrow 0=0$ und

$(\beta(1,3) = (0,1,0,1)\land\beta(2,3) = (1,1,1,0))\Rightarrow 1=1$

Sieht gut aus. Nun für Spielbrett Nr. 2 mit Belegung: $\beta(1,2) = (1,0,0,0)$, $\beta(1,3) = (1,1,0,0)$ und $\beta(2,3) = (1,1,1,0)$

$(\beta(1,2) = (1,0,0,0)\land\beta(1,3) = (1,1,0,0))\Rightarrow 0=1$ und

$(\beta(1,3) = (1,1,0,0)\land\beta(2,3) = (1,1,1,0))\Rightarrow 0=1$

Ne, hier klappt das leider nicht. Damit ist die angegebene Belegung bei Spielbrett 2 nicht zulässig. Das war es auch schon. Klingt spannend. Wollt Ihr das mal spielen? Bitte sehr: Tetravex. Zumindest ist das Browsergame unserem sehr ähnlich. Nur sind hier die Steine (die Menge $S$) hier vorgegeben und nicht nur eine Zeile des Bretts belegt.

Fragestellung: Wir suchen daher nach einer korrekten Belegung für ein Spielbrett. Es ist schnell einzusehen, dass das Spiel in $NP$ liegt: wir können eine Codierung angeben und diese dann in polynimieller Zeit auf Korrektheit testen. Dazu müssen wir nur eine Kontrollturingmaschine ($KTM$) angeben, die eine von uns gegebene Hilfseingabe auf Richtigkeit testet. Um die Belegung zu raten, verwenden wir eine $NTM$.

Der Beweis der $NP$-Vollständigkeit des Dominospiels

Wir haben hier zwei Dinge zu zeigen: $2D-DOMINO\in NP$ und anschließend die $NP$-Härte indem wir ein vollständiges Problem aus $NP$ auf unseres reduzieren. Haben wir keines, so müssen wir den mühsamen Weg selbst gehen und verzichten auf die Reduktion und beweisen die $NP$-Härte direkt. Aber kümmern wir uns zunächst um Punkt 1: $2D-DOMINO\in NP$. Dazu reicht es eine $KTM$ (oder $NTM$) anzugeben, die eine Hilfseingabe in Polynomzeit auf Korrektheit prüft (eine $NTM$ rät diese Hilfseingabe auch noch von alleine).

Um eine $NTM$ anzugeben, müssen wir zunächst das Spiel so formalisieren dass wir die Anfangsbelegung und unsere Steinchen auf das Eingabeband codieren. Die Menge $S$ der Spielsteine wird lexikographisch nummeriert und damit das ganze Spiel $D$ durch ein Wort $x$ über $\{0,1,\#\}^{*}$ auf das Eingabeband geschrieben.

Ein Beispiel wäre hilfreich: Nehmen wir z.B. das Spielbrett Nr. 1 von oben als Anfangsbelegung und basteln und daraus das gesamte Spiel $D_1$:

$\alpha(1,2) = (1,0,0,0)$, $\alpha(1,3) = (0,1,0,1)$ und $\alpha(2,3) = (1,1,1,0)$, alle anderen Felder sind leer

So haben das folgende Wort auf unserer $KTM$ (ich habe aus Faulheit nicht alle 16 Spielsteine auf das Band codiert, sondern nur den ersten $000$ und letzten $1111$, dazwischen mit Punkten $...$ gearbeitet):

$\gamma D(D_1) = 0\#0\#0\#0\#...\#1\#1\#1\#1\#\#\varepsilon\#1\#0\#0\#0\#0\#1\#0\#1\#\varepsilon\#\varepsilon\#1\#1\#1\#0\#\varepsilon\#\varepsilon\#\varepsilon$

Zunächst codieren wir also alle 16 Möglichkeiten der Steine, d.h. den Steinsatz auf das Band. Anschließend kommt die Anfangsbelegung $\alpha$ des Bretts, nachdem wir sie mit $\#\#$ von dem auf dem Band ebenfalls codierten Steinsatz getrennt haben. Nicht vergessen: mit $\varepsilon$ werden leere Felder bezeichnet.

Die Menge aller lösbaren Belegungen nennen wir:

$2D-DOMINO = \{x\in\{0,1,\#\}^{*}\mid x\in Bild(\gamma D)$ und ${\gamma D}^{-1}(x)$ ist lösbar $\}$.

Aufdröseln: $2D-DOMINO$ besteht also aus dem Wort $x$ über dem Alphabet $\{0,1,\#\}^{*}$, wobei $x$ ein Bild von $\gamma D$ und die Inverse von $\gamma D(x)$ lösbar sein muss. $\gamma D$ ist unsere Funktion, die als Parameter unser komplettes Spiel $D$ (Spielbrettgräße, Steine, Anfangsbelegung) als Wort bekommt und uns dazu das $x$ (das Spiel $D$ als codiertes Wort) ausgibt. Damit ist $D$ unser Definitionsbereich für die Funktion $\gamma D$ und $x$ liegt im Bildbereich von $\gamma D$. Wenn nun auch noch das Spiel $D$ lösbar ist (nicht jede Initialbelegung auf dem Spielbrett hat eine Lösung), so gehört das zum Spiel $D$ codierte Wort zur Menge $2D-DOMINO$. Anhand unseres Beispiels von Spielbrett Nr. 1 haben wir zusammengefasst:

$D_1 = (N,S,\alpha)$ (unser Spiel)

$S = \{\{0,0,0,0\}, \{0,0,0,1\}, ...,\{1,1,1,1\}\}$ (unsere Spielsteine)

$\alpha(1,2) = (1,0,0,0)$, $\alpha(1,3) = (0,1,0,1)$ und $\alpha(2,3) = (1,1,1,0)$ (unsere Anfangsbelegung)

$\gamma D(D_1) = 0\#0\#0\#0\#...\#1\#1\#1\#1\#\#\varepsilon\#1\#0\#0\#0\#0\#1\#0\#1\#\varepsilon\#\varepsilon\#1\#1\#1\#0\#\varepsilon\#\varepsilon\#\varepsilon$ (unser Spiel als codiertes Wort $x$)

$x\in Bild(\gamma D(D_1))$ (das Wort ist, wie man oben sehen kann im Bildbereich der Funktion $\gamma D$) und

$\gamma D^{-1}(x) = D_1)$ (die Inverse $\gamma D^{-1}$ gibt uns zu jedem $x$ ein $D$ zurück, d.h. zu jedem Codewort das zugehörige Spiel. Und das Spiel ist lösbar. Es gibt also eine vollständige Belegung $\beta$ für das Spiel $D_1$, die die oben genannten Regeln nicht verletzt).

Bitte beachtet, dass hier das ganze Spiel $D$ ohne zu testende Belegung auf das Band codiert wird. Die zu testende Belegung ist unsere Hilfseingabe $\beta$. Codieren wir also unser Spiel $D$ zusammen mit unserer zu testenden Hilfseingabe $\beta$ auf das Band, so können wir anhand der Regeln in quadratischer Zeit prüfen ob $\beta$ eine Lösung für $D$ ist.

Damit ist die Menge $2D-DOMINO\in NP$.

Bitte beachten: im Gegensatz zum vorherigen Beitrag zu KE3 haben wir hier zuerst die Zugehörigkeit von $2D-DOMINO$ zur $NP$ gezeigt indem wir eine $KTM$ angegeben haben, die mit unserem codierten Wort auf dem Eingabeband und unserer zu testenden Hilfseingabe diese Lösung überprüft. Nun müssen wir für die Vollständigkeit noch $2D-DOMINO$ ist $NP$-hart zeigen (ich Wiederhole mich häufig, was die Kriterien für die Vollständigkeit betrifft, aber besser zu viel als zu wenig).

Dazu zeigen wir, dass alle Mengen aus $M\in NP$ auf unsere Problemmenge $2D-DOMINO$ in polynomieller Zeit reduzieren lassen, formal ausgedrückt:

${M}\leq_{pol} 2D-DOMINO$

Denn das ist ja der Charme an der Vollständigkeit: können wir eine vollständige Menge reduzieren, können wir alle reduzieren (für eine Auffrischung, schaut in den letzten Beitrag zu KE3). Sobald das getan ist, gilt die Menge $2D-DOMINO$ als $NP$-vollständig.

Das Prinzip der in der KE4 beschriebenen Probleme ist es zu zeigen, dass man zunächst für alle Mengen $M\in NP$ diese auf $2D-DOMINO$ reduziert und dann $2D-DOMINO$ nutzt um es dann auf das Problem $SAT$, $SAT$ dann auf $3SAT$ usw. zu reduzieren und so die $NP$-Vollständigkeit der Probleme zu beweisen. D.h. haben wir eine Menge initial als $NP$-Vollständig nachgewiesen, so können wir durch einfache Reduzierung andere Mengen sofort auch als $NP$-Vollständig nachweisen (hier sei auf den Abschnitt zu Cook im Beitrag zu KE3 verwiesen).

Zeitbedingt muss ich den Beweis der $NP$-Härte für $2D-DOMINO$ überspringen, werde versuchen ihn für $SAT$ und $3SAT$ im nächsten Beitrag nachzuholen, da $SAT$ doch häufiger anzutreffen ist als $2D-DOMINO$. Wer eine schöne Beschreibung des Beweises aus dem Skript hat, immer her damit.

Antwort zum Lernziel: zunächst wird wie bei allen Beweisen der Vollständigkeit gezeigt, dass sich $2D-DOMINO$ in $NP$ befindet indem man ein Verfahren angibt, dass das Problem in nichtdeterministischer polynomieller Zeit löst, d.h. eine $KTM$, dass unsere Prüfbelegung (sog. Hilfseingabe) auf Korrektheit prüft. Anschließend zeigt man die $NP$-Härte von $2D-DOMINO$ mittels zwei Möglichkeiten:

1. die leichte: wir reduzieren $2D-DOMINO$ polynomiell auf ein bekanntes, $NP$-schweres Problem indem man ein Verfahren angibt, dass diese Reduktion in polynomieller Zeit schafft oder

2. die schwere: wenn wir kein Problem haben (Henne-Ei-Problem), müssen wir eines angeben, bei dem einzusehen ist, dass es definitiv in $NP$ liegt (ob es praxistauglich ist, ist egal). Man konstruiert sich sozusagen ein Problem. Auf dieses wird dann $2D-DOMINO$ reduziert.

Stephen A. Cook hat uns die Arbeit aber abgenommen und $SAT$ als $NP$-vollständig bewiesen, so dass wir die $NP$-Vollständigkeit von $2D-DOMINO$ beweisen könnten wenn wir es auf $SAT$ zurückführen.

Lernziel 2

Wie beweist man die $NP$-Vollständigkeit einer Menge?

Antwort zum Lernziel: Doppelt hält besser: Für die $NP$-Vollständigkeit eines Problems müssen wir also zuerst nachweisen, dass es in $NP$ liegt (dazu geben wir eine $KTM$ an, die das Problem in Polynomzeit mit einer gegebenen Hilfseingabe entscheiden kann. Oder eine $NTM$ zum vorherigen Ergebnis-orakeln, denn das orakeln ist das $N$ in $NTM$). Anschließend muss noch die $NP$-härte nachgewiesen werden, indem wir ein vollständiges Problem in Polynomzeit auf unseres reduzieren oder auf Reduktion verzichten und die $NP$-Härte direkt nachweisen.

Wenn wir also noch kein $NP$-vollständiges Problem haben, dass wir reduzieren können, haben wir ein klassisches Henne-Ei-Problem. Zum Glück gibt es kluge Leute, die das auch ohne die Reduzierung geschafft haben. Und sie leben auch noch: einer davon ist Stephen A. Cook mit seinem berühmten Satz von Cook. In diesem zeigte er die Vollständigkeit des $SAT$-Problems. Wir wollen den Beweis mal nachvollziehen, so als Kompensation zum fehlenden $2D-DOMINO$-Beweis von oben.

Im nächsten Beitrag geht es dann entsprechend um $SAT$.

Datum: 18. Mai 2013
Kategorie: Theoretische Informatik
Kommentarfeed: RSS 2.0 • Trackback: Trackback-Url

Sie können zum Ende springen und ein Kommentar hinterlassen. Pingen ist im Augenblick nicht erlaubt.