TI: Beweis der Addition zweier Register mit einer Registermaschine
Um zu zeigen, dass eine Zahlenfunktion berechenbar ist muss man nachweisen, dass man die Funktion mit der allgemeinen Maschine berechnen und die komplexen Funktionen und Tests der allgemeine Registermaschine dann durch eine normale Registermaschine ausdrücken kann (die korrekte Funktion dieser vorausgesetzt bzw. bewiesen). Auch müssen die im Flussdiagramm vorkommenden Tests rekursiv, d.h. entscheidbar sein. Wir kümmern uns hier um Ersteres. Der Umweg über die allgemeine Registermaschine wird gegangen um sich die Schreibarbeit der komplexen Funktionen nur einmal machen zu müssen. Hat man z.B. die Multiplikation als komplexe Operation mit einer normalen Registermaschine (nur mit den Operationen Addition/Subtraktion, arithmetische Differenz und Test auf 0) bewiesen, kann man diese ab sofort in seiner allgemeinen Registermaschine nutzen.
Formal definiert bedeutet es, dass eine Funktion 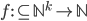 dann berechenbar ist, genau dann wenn es eine k-stellige Registermaschine gibt mit
dann berechenbar ist, genau dann wenn es eine k-stellige Registermaschine gibt mit 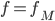 .Bei
.Bei 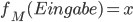 ist x hierbei das Ergebnis welches nach einem Durchlauf (man ist bei HALT gelandet oder wenn es kein Ende gibt bei
ist x hierbei das Ergebnis welches nach einem Durchlauf (man ist bei HALT gelandet oder wenn es kein Ende gibt bei 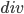 ) der Registermaschine (das als Flussdiagramm dargestellt ist) in Register
) der Registermaschine (das als Flussdiagramm dargestellt ist) in Register 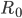 steht. Informal ausgedrückt bedeutet es, dass die Funktion
steht. Informal ausgedrückt bedeutet es, dass die Funktion 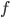 durch Maschine
durch Maschine 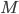 berechnet werden kann und die Ergebnisse für jede Eingabe für
berechnet werden kann und die Ergebnisse für jede Eingabe für 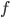 und
und 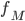 gleich sind: eben
gleich sind: eben 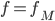 .
.
Nehmen wir als Beispiel die Addition von zwei Registern 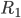 und
und 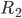 durch eine allgemeine Registermachine. Sie berechnet das Ergebnis und legt es dann im Ergebnisregister
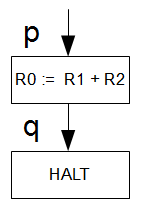
durch eine allgemeine Registermachine. Sie berechnet das Ergebnis und legt es dann im Ergebnisregister 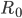 ab. Hier das zugehörige und unglaublich komplexe Flussdiagramm dazu.
ab. Hier das zugehörige und unglaublich komplexe Flussdiagramm dazu.
Da es eine komplexe Funktion ist müssen wir sie jedoch mit einer normalen Registermaschine und den drei erlaubten Operationen (Addition und Subtraktion von , sowie Test auf
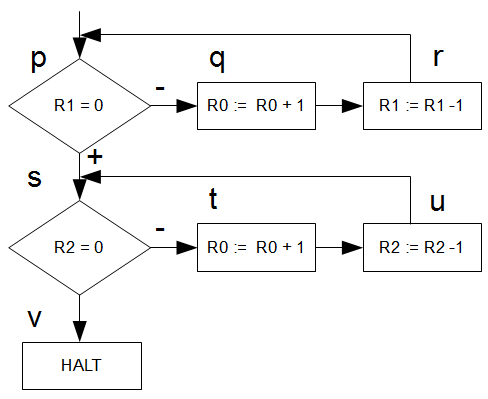
, sowie Test auf 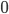 ) abbilden und zeichnen uns hierzu ein passendes Flussdiagramm. Dieses ist nur unwesentlich komplexer.
) abbilden und zeichnen uns hierzu ein passendes Flussdiagramm. Dieses ist nur unwesentlich komplexer.
Umgangssprachlich macht die normale Registermaschine folgendes: die inkrementiert das Register 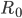 zunächst genau
zunächst genau 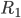 mal und dekrementiert
mal und dekrementiert 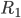 bei jedem Durchlauf der ersten Schleife (
bei jedem Durchlauf der ersten Schleife (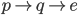 ). Anschließend wird es in Block
). Anschließend wird es in Block 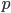 wieder auf 0 geprüft. Sollte das Register
wieder auf 0 geprüft. Sollte das Register 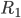 tatsächlich 0 sein, bewegen wir uns dann zum Block
tatsächlich 0 sein, bewegen wir uns dann zum Block 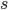 um in der zweiten Schleife (
um in der zweiten Schleife (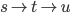 ) das Selbe nochmal mit Register
) das Selbe nochmal mit Register 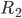 zu veranstalten und
zu veranstalten und 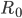 weitere
weitere 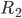 Mal zu inkrementieren. Damit wird
Mal zu inkrementieren. Damit wird 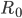 genau
genau 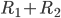 Mal inkrementiert und so die Addition von Register
Mal inkrementiert und so die Addition von Register 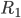 und
und 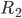 bewerkstelligt. Einfach, nicht? Jetzt stellt sich nur die Frage, wie wollen wir die korrekte Funktionalität unserer normalen Registermaschine beweisen. Alle
bewerkstelligt. Einfach, nicht? Jetzt stellt sich nur die Frage, wie wollen wir die korrekte Funktionalität unserer normalen Registermaschine beweisen. Alle 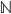 durchtesten? Ne, lieber nicht.
durchtesten? Ne, lieber nicht.
Der Beweis
Der Beweis, dass die Funktion 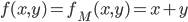 berechenbar ist gliedert sich selbst in folgende Schritte:
berechenbar ist gliedert sich selbst in folgende Schritte:
- allgemeine Registermaschine als Flussdiagramm zeichnen, die die Funktion berechnet. Ggf. die korrekte Funktion auch mit vollständiger Induktion beweisen. Hier verzichten wir darauf, da es für das kleine Flussdiagramm oben offensichtlich ist. Ebenso ist hier darauf zu achten, dass jeder vorkommende Test entscheidbar ist.
- alle komplexen Operationen der allgemeinen Registermaschine durch eine normale Registermaschine als Flussdiagramm ausdrücken, wo man nur die aus der Definition für normale Registermaschinen erlaubten Funktionen Addition und Subtraktion von
 , sowie Test auf
, sowie Test auf 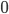 durchführen darf. Auch hier bitte auf entscheidbare Tests achten.
durchführen darf. Auch hier bitte auf entscheidbare Tests achten. - nun hat man für jede komplexe Operation ein Flussdiagramm, deren korrekte Funktion man mit vollständiger Induktion beweisen muss.
Das Flussdiagramm aus Schritt 2 ist oben dargestellt. Da wir nur eine komplexe Operation (die Addition) haben, haben wir nur ein Flussdiagramm für eine normale Registermaschine. Man überzeuge sich, dass nur die erlaubten 3 Operationen benutzt werden. Überzeugt? Gut! Fangen wir mit dem Induktionsbeweis an.
Wir prüfen zunächst de Fälle, die wir als Eingabe haben und leiten hieraus die Induktionsbehauptungen ab:
Wir möchten jede natürliche Zahl (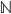 ) addieren können. Im Endeffekt sind diese dann fest und wir haben nur eine unterschiedliche Anzahl an Einzelschritten, die wir durch das Programm gehen müssen bis das Ergebnis im Register
) addieren können. Im Endeffekt sind diese dann fest und wir haben nur eine unterschiedliche Anzahl an Einzelschritten, die wir durch das Programm gehen müssen bis das Ergebnis im Register 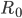 steht. Abhängig von den Eingabewerten. Da wir zwei Schleifen haben, können wir für diese auch zwei Induktionsbehauptungen aufstellen.
steht. Abhängig von den Eingabewerten. Da wir zwei Schleifen haben, können wir für diese auch zwei Induktionsbehauptungen aufstellen.
Man sieht leicht, dass wir die erste Schleife genau 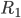 Mal durchlaufen und wieder in Block
Mal durchlaufen und wieder in Block 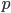 landen. Ist z.B.
landen. Ist z.B. 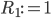 , so sind 3 Einzelschritte notwendig bis wir
, so sind 3 Einzelschritte notwendig bis wir 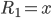 erneut auf 0 testen und die Schleife verlassen. Das als Registerbelegung erwartete Gesamtergebnis ist also
erneut auf 0 testen und die Schleife verlassen. Das als Registerbelegung erwartete Gesamtergebnis ist also 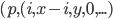 , wobei
, wobei 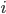 die Anzahl der Schleifendurchläufe und somit auch die Anzahl der Inkrementierungen von
die Anzahl der Schleifendurchläufe und somit auch die Anzahl der Inkrementierungen von 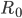 (eben
(eben 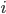 im Ergebnis) und Dekrementierungen von
im Ergebnis) und Dekrementierungen von 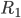 (eben
(eben 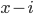 im Ergebnis) ist. Der Rest bleibt unangetastet (
im Ergebnis) ist. Der Rest bleibt unangetastet (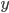 und
und 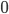 ) Damit ergibt sich schon die erste Induktionsannahme in Abhängigkeit von x:
) Damit ergibt sich schon die erste Induktionsannahme in Abhängigkeit von x:
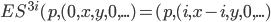
Das Ergebnis ist so wie wir gewollt haben: ist 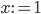 , so haben wir nur einen Schleifendurchlauf, genau 3 Einzelschritte und am Ende die Registerbelegung
, so haben wir nur einen Schleifendurchlauf, genau 3 Einzelschritte und am Ende die Registerbelegung 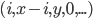 und wir landen wieder im Block
und wir landen wieder im Block 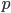 . Ist
. Ist 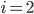 , so haben wir zwei Schleifendurchläfe, somit 6 Einzelschritte und landen wieder bei
, so haben wir zwei Schleifendurchläfe, somit 6 Einzelschritte und landen wieder bei 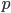 . Die Behauptung scheint also korrekt. Fehlt nur noch der Induktionsbeweis für den Dominoeffekt damit wir nicht unendlich viele Fälle durchtesten müssten.
. Die Behauptung scheint also korrekt. Fehlt nur noch der Induktionsbeweis für den Dominoeffekt damit wir nicht unendlich viele Fälle durchtesten müssten.
Wir führen für die oben aufgestellte
Annahme:
=
einen Induktionsbeweis über
durch. Zu beweisen ist:
Behauptung:
der Einfachheit halber ausrechnen:
D.h. am Ende unseres Beweises muss
rauskommen. Wir fangen also an:
(wir setzen hier den rechten Teil der Annahme von oben als "Induktionsschritt" ein, mit
haben wir unser "+1" um es mal nicht unbedingt formal korrekt auszudrücken und spielen jetzt das Flussdiagramm durch)
=
(nun sind wir in Block q)
=
(nun sind wir in Block r)
=
(am Ende sind wir in Block p)
Und siehe da: das Ergebnis entspricht dem rechten Teil der Behauptung. Damit haben wir die Schleife bewiesen.
Fehlt uns noch die Annahme für die andere Schleife. Diese ist analog zur ersten Schleife herauszufinden. Wir starten bei Block 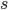 und haben die Eingabe
und haben die Eingabe  , da wir x bereits aus der vorhergehenden Schleife wissen,
, da wir x bereits aus der vorhergehenden Schleife wissen, 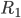 aufgrund der Dekrementierung auf
aufgrund der Dekrementierung auf 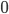 ist und somit nur noch
ist und somit nur noch 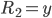 verbleibt, was wir in dieser Schleife genau
verbleibt, was wir in dieser Schleife genau 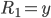 Mal dekrementieren und
Mal dekrementieren und 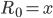 somit um die gleiche Anzahl inkrementieren. Wir haben hier ebenfalls drei Schritte bis wir wieder in Block
somit um die gleiche Anzahl inkrementieren. Wir haben hier ebenfalls drei Schritte bis wir wieder in Block 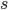 angekommen sind. Als Ergebnis erwarten wir somit wieder in Block
angekommen sind. Als Ergebnis erwarten wir somit wieder in Block 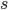 zu sein und folgende Registerbelegung zu haben:
zu sein und folgende Registerbelegung zu haben:  , da
, da 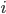 genau die Anzahl ist, die wir die Schleife durchlaufen und
genau die Anzahl ist, die wir die Schleife durchlaufen und 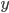 dekrementiert und
dekrementiert und  inkrementiert haben. Hier ist dann auch schon die Annahme:
inkrementiert haben. Hier ist dann auch schon die Annahme: 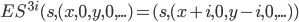 . Für diese führen wir nun den Induktionsbeweis über
. Für diese führen wir nun den Induktionsbeweis über 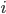 durch:
durch:
Annahme:
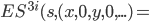
Zu beweisen ist die Behauptung:
Auch hier einfach ausrechnen:
D.h. am Ende unseres Beweises muss
rauskommen.
Wir fangen an:
(wieder den rechten Teil der Annahme einsetzen und ab jetzt das Diagramm durchspielen)
=
(nun sind wir in Block t)
=
(nun sind wir in Block u)
=
(nun sind wir an Ende wieder in Block s)
Und auch hier: das Ergebnis entspricht dem rechten Teil der Behauptung. Damit haben wir auch die zweite die Schleife bewiesen.
Die Fälle für 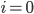 (d.h. man springt im Flussdiagramm direkt durch bis zum
(d.h. man springt im Flussdiagramm direkt durch bis zum 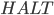 ) habe ich ausgelassen, da sie durch einfaches Ausrechnen offensichtlich sind. Durch die drei Schritte (Flussdiagramm einer allgemeinen Maschine erstellen, Flussdiagramm einer normale Maschine für jede in der allgemeinen Maschine verwendete komplexe Funktion erstellen, Beweis der Korrektheit der normalen Maschinen durch vollständige Induktion) haben wir bewiesen, dass unsere allgemeine Maschine
) habe ich ausgelassen, da sie durch einfaches Ausrechnen offensichtlich sind. Durch die drei Schritte (Flussdiagramm einer allgemeinen Maschine erstellen, Flussdiagramm einer normale Maschine für jede in der allgemeinen Maschine verwendete komplexe Funktion erstellen, Beweis der Korrektheit der normalen Maschinen durch vollständige Induktion) haben wir bewiesen, dass unsere allgemeine Maschine 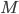 die Funktion
die Funktion 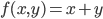 berechnet. Damit gilt
berechnet. Damit gilt 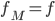 .
.
Wie immer: bei Fehlern bitte Bescheid geben.
Buchempfehlung

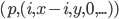
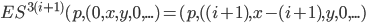
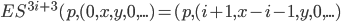
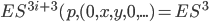
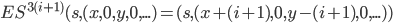
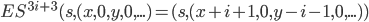
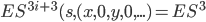



Oktober 9th, 2012 12:47
Schöne Seite,
genau mein Thema 🙂
"= ES(r,(i+1,x−i,y,0,...)) (nun sind wir in Block r)"
Wo ist denn im Flussdiagramm oben der Block r zu besichtigen?
Gruß aus Berlin
Mike
Oktober 9th, 2012 12:57
Ah, Du hast Recht! Der Block e sollte eig. Block r sein 🙂 Danke. Wird gleich geändert.
Oktober 17th, 2012 17:02
Hi,
die Zusammenfassungen finde ich bisher sehr gut. Schön wenn man den Inhalt nochmal mit anderen Worten lesen kann. Hilft mir sehr.
Was mich aber verwirrt ist der Titel des Posts. "Beweis der Multiplikation mit einer Registermaschine" - ich sehe nur die Addition.
Gruß aus Berlin
Martin
Oktober 17th, 2012 17:11
Hallo Martin,
Du hast Recht! Ich wollte zunächst die Multiplikation beweisen, habe mich dann aber für die Addition entschieden damit es näher am Kursstoff ist.
Danke für den Hinweis.