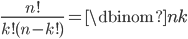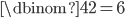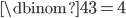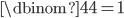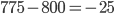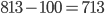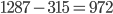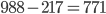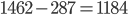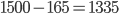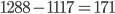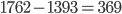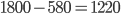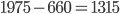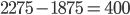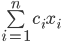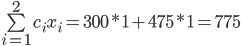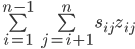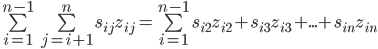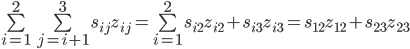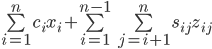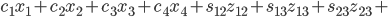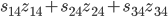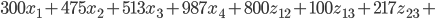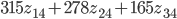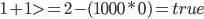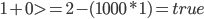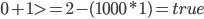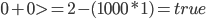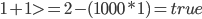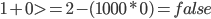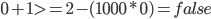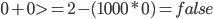1772: E-Business Management (Standardisierung)
Die Aufgabe aus der Einsendeaufgabe 1 erinnert stark an Simplex. Im Grunde geht es um die Frage, ob die Mitglieder eines Netzwerks einem bestimmten Standard folgen sollen, oder nicht. Und wie alles in Netzwerken wird auch das Anhand von Transaktionskosten zwischen den beteiligten Knoten entschieden. Dazu hat EA1 eine Tabelle aufgestellt, die anzeigt wie viel zwischen den Knoten 1 und 2 eingespart wird, wenn der neue Standard zwischen 1 und 2 eingeführt wird:
Einsparungen
- Standard eingeführt zwischen 1 und 2: 800 EUR Einsparung
- Standard eingeführt zwischen 1 und 3: 100 EUR Einsparung
- Standard eingeführt zwischen 1 und 4: 314 EUR Einsparung
- Standard eingeführt zwischen 2 und 3: 217 EUR Einsparung
- Standard eingeführt zwischen 2 und 4: 278 EUR Einsparung
- Standard eingeführt zwischen 3 und 4: 165 EUR Einsparung
Die weiteren Zellen - z. B. Standard zwischen 1 und 1 oder Standard zwischen 3 und 2 - sind nicht gefüllt weil die Betrachtung der Kommunikation zwischen Knoten 1 und 1 unsinnig ist und der Kommunikationsweg zwischen 3 und 2 der Gleiche ist, wie zwischen 2 und 3. Es reicht also nur einen Weg zu betrachten. Würden sich die Kosten für Hin- und Rückweg unterscheiden, müsste man natürlich auch den Rückweg mit in die Betrachtung einbeziehen.
Die Frage ist also:
Auf welchen Knoten kann ich den Standard einführen, um die größten Einsparungen zu erzielen?
Und in diesem Moment heißt die Antwort noch: An allen!
Und warum? Weil wir noch keine Kosten für die Einführung definiert haben. Wäre ja auch zu schön gewesen, wenn man irgendwo Einsparungen realisieren kann, ohne Kosten zu haben. Die Minimierungsfunktion wäre in diesem Fall ziemlich witzlos. Aber dafür das Ergebnis recht eindeutig. It's something.
Kosten
Kümmern wir uns daher um die Kosten. Diese sind für die 4 Knoten:
- Kosten für die Einführung des Standards auf Knoten 1: 300 EUR
- Kosten für die Einführung des Standards auf Knoten 2: 475 EUR
- Kosten für die Einführung des Standards auf Knoten 3: 513 EUR
- Kosten für die Einführung des Standards auf Knoten 4: 987 EUR
Und jetzt können wir die Frage erneut stellen:
Auf welchen Knoten kann ich den Standard einführen, um die größten Einsparungen zu erzielen?
Aber die Antwort ist hier nicht mehr so einfach.
Versuchen wir dennoch unser Glück. Führen wir einfach auf jedem Knoten den Standard ein, so haben wir folgende Kosten: 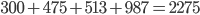 EUR bei Einsparungen von
EUR bei Einsparungen von 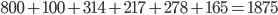 EUR. Lohnt sich nicht auf den ersten Blick, oder?
EUR. Lohnt sich nicht auf den ersten Blick, oder?
Aber dafür können wir unsere Frage etwas präziser stellen:
Auf welchen Knoten muss ich den Standard einführen, um bei den geringsten Kosten die größten Einsparungen zu erzielen?
Unwichtiges streichen
Um jetzt ein Modell aufzustellen, müssen wir uns klar machen, dass wir bei 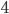 Knoten insgesamt
Knoten insgesamt 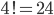 Kombinationsmöglichkeiten haben. Obwohl z. B. die Permutationen
Kombinationsmöglichkeiten haben. Obwohl z. B. die Permutationen 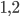 und
und 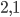 unterschiedlich sind, haben wir kein Interesse an ihnen. Denn das Ergebnis wäre gleich (Kosten:
unterschiedlich sind, haben wir kein Interesse an ihnen. Denn das Ergebnis wäre gleich (Kosten: 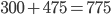 EUR gegenüber
EUR gegenüber 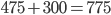 EUR). Das gilt natürlich auch für die Permutation
EUR). Das gilt natürlich auch für die Permutation 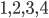 und
und 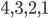 . Auch an der Einführung des Standards auf einem einzigen Knoten ist nicht spannend, also streichen wir auch das. Nehmen wir das mal Stück für Stück auseinander:
. Auch an der Einführung des Standards auf einem einzigen Knoten ist nicht spannend, also streichen wir auch das. Nehmen wir das mal Stück für Stück auseinander:
(Kombination: 1 aus 4: Einführung Standard nur auf einem Knoten) - kein Interesse
(Kombination: 2 aus 4: Einführung Standard auf zwei Knoten) - kein Interesse an der Reihenfolge, wie z. B. bei
und
sowie an
oder
. Bleiben hier nur noch 6 spannende Paare:
-
-
-
-
-
: (Kombination: 3 aus 4: Einführung Standard auf drei Knoten) - hier gilt das gleiche wie bei
. Es bleiben nur die Tripel
-
-
.
: (Kombination: 4 aus 4: Einführung Standard auf vier Knoten) - das wird am einfachsten. Was bleibt, ist die Einführung auf allen 4 Knoten
.
Die Kombination 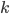 aus
aus 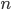 ohne Wiederholung ist der Binomialkoeffizient und wird mit folgender Formel ausgedrückt:
ohne Wiederholung ist der Binomialkoeffizient und wird mit folgender Formel ausgedrückt:
Wir suchen uns die Kombinationen 2, 3 und 4. Setzen wir das in die Formel ein, so landen wir bei:
Es sind also 11 Kombinationen zu berechnen (Kosten minus Einsparung = Ergebnis). Prüfen wir, ob's wirklich 11 sind:
=
=
=
=
=
=
=
=
=
=
=
Ja, sind 11. Ab hier ist zu sehen, dass das beste Kosten / Einsparungs-Verhältnis die Einführung des Standards auf Knoten  und
und 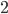 bietet und uns einen "Gewinn" (negative, indirekte Kosten) von 25 EUR beschert. Es sieht zwar was doof aus, da wir Kosten + Einsparung rechnen, aber das ist eine Minimierungsfunktion, die wir aufstellen wollen. Wenn wir das umdrehen (Einsparung - Kosten), haben wir eine Maximierungsfunktion, können aber nicht so schön rechnen.
bietet und uns einen "Gewinn" (negative, indirekte Kosten) von 25 EUR beschert. Es sieht zwar was doof aus, da wir Kosten + Einsparung rechnen, aber das ist eine Minimierungsfunktion, die wir aufstellen wollen. Wenn wir das umdrehen (Einsparung - Kosten), haben wir eine Maximierungsfunktion, können aber nicht so schön rechnen.
Das Modell
Aber wie gießen wir unsere Erkenntnis in ein Modell? Wir brauchen Entscheidungsvariablen 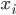 , die uns anzeigen, ob der Standard an Knoten
, die uns anzeigen, ob der Standard an Knoten 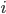 etabliert ist. Das befähigt uns dazu die Parameter Kosten
etabliert ist. Das befähigt uns dazu die Parameter Kosten 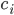 und Einsparungen
und Einsparungen 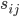 (wenn Standard an Knoten
(wenn Standard an Knoten 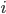 und
und 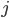 eingeführt wurde ist) auszurechnen.
eingeführt wurde ist) auszurechnen.
Das bedeutet: WENN 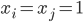 (Standard ist an Knoten
(Standard ist an Knoten 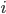 und
und 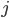 etabliert), sind die Kosten
etabliert), sind die Kosten 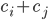 und die Einsparungen
und die Einsparungen 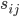 . Wie euch aufgefallen ist, nutzen wir für unser WENN / DANN - Konstrukt die Entscheidungsvariable
. Wie euch aufgefallen ist, nutzen wir für unser WENN / DANN - Konstrukt die Entscheidungsvariable 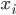 , wenn der Standard auf Knoten
, wenn der Standard auf Knoten 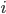 eingeführt wurde. Wenn Die Entscheidungsvariable 1 ist, so werden die Kosten mit 1 multipliziert. Ansonsten ist sie 0, die Kosten werden mit 0 multipliziert, sind also nicht vorhanden.
eingeführt wurde. Wenn Die Entscheidungsvariable 1 ist, so werden die Kosten mit 1 multipliziert. Ansonsten ist sie 0, die Kosten werden mit 0 multipliziert, sind also nicht vorhanden.
Das wäre der erste Teil der Minimierungsfunktion aus dem Skript:
Vereinfachen wir als Beispiel unsere Rechnung und probieren das mal mit zwei Knoten aus. Standard eingeführt auf Knoten 1 und 2: 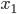 und
und 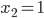 . Kosten:
. Kosten: 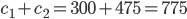 (und Einsparungen
(und Einsparungen 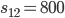 ). Sieht gut aus.
). Sieht gut aus.
Das Problem hier ist, dass wir damit nur die Kosten für die Einführung des Standards aufsummiert haben. Wenn wir das minimieren führt uns das nur dazu, dass wir wissen an welchen Knoten wir mit den geringsten Kosten den Standard einführen können. Die Relation zu den Einsparungen fehlt uns noch!
Das wäre der 2. Teil aus dem Skript:
Der ist ein bisschen aufwändiger. Lasst euch von dem 2. Summenzeichen nicht irritieren, das ist nur eine Doppelsumme. Diese können wir auch ausschreiben. Sieht nur dann nicht mehr so fancy aus.
Exkurs: Doppelsumme
Probieren wir das einfach mal an 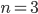 .
.
Beispiel:
Bevor wir den 2. Teil der Minimierungsfunktion im Detail auseinander nehmen, müssen wir uns über die folgende Relation im klaren sein (Achtung, wichtig!): Wenn wir den Standard an Knoten 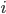 und
und 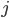 nicht einführen, entstehen uns zwar direkt keine Kosten
nicht einführen, entstehen uns zwar direkt keine Kosten 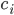 und
und 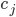 , aber uns entgehen auch die damit verbundenen Einsparungen
, aber uns entgehen auch die damit verbundenen Einsparungen 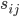 , die als indirekte Kosten betrachtet werden können.
, die als indirekte Kosten betrachtet werden können.
Beispiel: Einführung den Standards auf Knoten 1 und 2 ergibt Kosten von 775 EUR und Einsparungen von 800 EUR, so dass wir unter'm Strich mit 25 EUR nach Hause gehen. Die Nicht-Einführung des Standards auf den beiden Knoten ergibt keine direkten Kosten, aber entgangene Einsparungen von 800 EUR. Damit sind wir 25 EUR im Minus.
Unsere Rechnung der vollständigen Kosten (direkt und indirekt) müsste im Falle der Standard-Einführung so aussehen: 300*1 + 475*1 + 0*800 = 775.
Führen wir den Standard nicht ein, haben wir: 300*0 + 475*0 + 1*800 = 800 an indirekten Kosten durch entgangene Einsparung.
Der Bezug von Kosten zu entgangenen Einsparungen wird durch die Verbindung der Entscheidungsvariablen 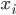 und
und 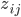 erreicht. Sind
erreicht. Sind 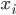 und
und 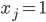 (Standard wird eingeführt), so ist die Entscheidungsvariable
(Standard wird eingeführt), so ist die Entscheidungsvariable 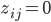 (uns entgehen keine Einsparungen, es entstehen aber direkte Kosten). Sind
(uns entgehen keine Einsparungen, es entstehen aber direkte Kosten). Sind 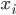 und
und 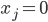 (Standard wird nicht eingeführt), so ist die Entscheidungsvariable
(Standard wird nicht eingeführt), so ist die Entscheidungsvariable 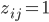 (uns entgehen Einsparungen und damit entstehen indirekte Kosten). Und da wir Interesse haben unsere gesamten Kosten zu minimieren, führen wir beides nun zusammen.
(uns entgehen Einsparungen und damit entstehen indirekte Kosten). Und da wir Interesse haben unsere gesamten Kosten zu minimieren, führen wir beides nun zusammen.
Bei 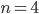 würde die ausgeschriebene Funktion wie folgt aussehen:
würde die ausgeschriebene Funktion wie folgt aussehen:
Das erste Summenzeichen:
(direkte Kosten)
Die zwei weiteren Summenzeichen:
(indirekte Kosten durch entgangene Einsparungen)
Zusammen:
Und das ist unsere ganze Minimierungsfunktion für 4 Knoten. Setzen wir die Kosten und Einsparungen mal ein.
Min
Wir sind fast fertig. Uns fehlt nur noch eines.
Nebenbedingungen
Wir haben diese zwar schon in Prosa formuliert, müssen das aber in mathematischer Notation noch nachholen und eine kleine Ungenauigkeit beseitigen. Rekapitulieren wir: Folgende zwei Bedingungen sind zu formulieren:
- Wenn der Standard auf Knoten 1 und 2 eingeführt wurden, so sind uns direkte Kosten entstanden, aber gleichzeitig Einsparungen erzielt worden (oder nicht, siehe Fallunterscheidung). Ist der Standard nicht eingeführt worden, sind uns in Form von entgangenen Einsparungen indirekte Kosten entstanden. Da wir diesen Sachverhalt bereis in den Entscheidungsvariablen
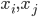 und
und 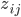 festgehalten haben, müssen wir deren Beziehung nun mathematisch formulieren.
festgehalten haben, müssen wir deren Beziehung nun mathematisch formulieren.
Wir haben folgende Fälle zu unterscheiden:
- Eingeführt auf Knoten
, aber nicht auf Knoten
. Es entstanden also nur Kosten für Knoten
. Einsparungen dürfen keinesfalls vorhanden sein, da uns für die Kommunikation der Knotenpartner fehlt.
Damit muss(indirekte Kosten sind entstanden) sein. Ist
, so darf die NB nicht erfüllt sein.
- Gleiches gilt anders herum für die Einführung nur bei
.
- Gar keine Einführung. Es muss gelten:
(indirekte Kosten sind entstanden). Wenn wir
setzen, darf die NB nicht erfüllt sein.
- Einführung bei beiden Knoten. Hier räumen wir die Ungenauigkeit aus (danke an die Kursbetreuung für den Hinweis!): Obwohl der Standard eingeführt wurde, heißt es nicht, dass man ihn auch nutzen muss. Man darf!Bedeutet: Obwohl wir direkte Kosten für die Einführung hatten, müssen wir die Einsparungen nicht realisieren (auch wenn das natürlich sinnlos wäre) und können uns ökonomisch sinnfrei direkte und indirekte Kosten aufhalsen, d. h. die beiden Fälle
(keine Nutzung des Standards = keine Einsparungen = indirekte Kosten) und
(Nutzung des Standards = Einsparungen realisiert = keine indirekten Kosten) sind beide erlaubt, auch wenn der Standard an beiden Knoten eingeführt wurde. Die NB muss daher in beiden Fällen "true" zurückliefern.
Hier greift das Skript in die mathematische Trickkiste und formuliert alle 4 Bedingungen mit Hilfe einer großen, positiven Konstante 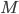 .
.
(NB 1.5)
Wenn wir für alle möglichen Fälle die Werte in die Nebenbedingung einsetzen, muss die Nebenbedingung folgende Fälle abfangen und folgende Ergebnisse zurückliefern:
Und das macht sie auch, rechnet das ruhig nach.
Bleibt nur noch NB 1.6. Aber die ist - das wollte ich immer schon einmal sagen - trivial.
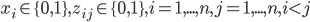 (NB 1.6)
(NB 1.6)
Sie sagt nichts weiter aus, als dass unsere Variablen binär sind und unser Zähler 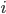 kleiner als
kleiner als 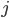 sein muss (wäre
sein muss (wäre 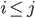 , so gäbe es z. B.
, so gäbe es z. B. 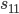 , d. h. einen Einsparungsbetrag von Knoten 1 zu Knoten 1).
, d. h. einen Einsparungsbetrag von Knoten 1 zu Knoten 1).