TIA: Bild- und Projektionssatz (Lernziele KE6 2/4, Update)
Update: Schnitzer im Projektionssatz aufgefallen. Fixed.
Als ich die letzten Beiträge zu Kurseinheit 5 von TIA durchgegangen bin, ist mir aufgefallen, dass einige Beweise doch noch nicht so nachvollziehbar sind, wie ich das gerne hätte.
Nach dem Editieren kam ich auf eine Seitenzahl von über 20. Schon wieder. Da blieb mir also nichts anderes übrig, als den Beitrag zu KE6 erneut zu trennen. Schwierigkeiten machten mir aber die Kommentare zu den Lernzielen als alles noch ein einzelner Beitrag war. Diese zu verschieben war ohne manuellen Eingriff in die Datenbank nicht möglich.
Solltet Ihr daher auf Kommentare treffen, die nicht unbedingt zu dem Beitrag hier passen: meine Schuld. Sie gehören dann zu einem der drei anderen.
Dieser Artikel ist brandneu und die anderen Beiträge zu KE6 sind teilweise massiv überarbeitet worden. Eine erneute Lektüre könnte sich also lohnen wenn Ihr bei KE6 der theoretischen Informatik A noch strauchelt und den Sachverhalt gerne mal in anderen Worten gelesen hättet.
Lange Rede, kurzer Sinn: Das sind also die Beiträge zu Kurseinheit 6.
- TIA: Rekursive und rekursiv-aufzählbare Mengen (Lernziele KE6, 1/4)
- TIA: Bild- und Projektionssatz (Lernziele KE6 2/4)
- TIA: Halte- Äquivalenz- und Korrektheitsproblem, Reduzierbarkeit, Satz von Rice (Lernziele KE6, 3/4)
- TIA: Gödel'scher Unvollständigkeitssatz (Lernziele KE6, 4/4)
Dieser dreht sich komplett um den Bild- und Projektionssatz. Ursprünglich war er nicht einmal eine halbe Seite lang. Als ich den Beweis dann Schritt für Schritt nachvollzog, wuchs er auf die aktuelle Größe heran. Tja, und da ist er nun.
Lernziel 5
Charakterisierung der r.a. Mengen durch Bild- und Projektionssatz
Die Charakterisierung ist wie folgt definiert:
1.
ist r.a. gdw.
oder
für ein
2.
ist r.a. gdw. es eine rekursive Menge
gibt mit
Nr. 1 bedeutet, dass eine Menge 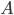 dann rekursiv ist, wenn sie von einer totalen, rekursiven Funktion
dann rekursiv ist, wenn sie von einer totalen, rekursiven Funktion 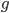 aufgezählt werden kann, d.h. dass
aufgezählt werden kann, d.h. dass 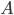 Bild dieser Funktion ist.
Bild dieser Funktion ist.
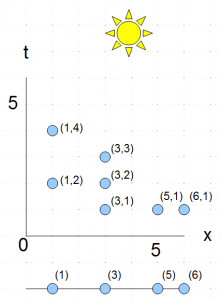
Nr. 2 ist der Projektionssatz: eine Menge ist r.a. wenn sie die Projektion einer rekursiven Menge ist. Das Bild im Skript ist relativ eindeutig wenn man weiß, nach was man schauen muss. Ich nehme hierzu ein konkretes Beispiel mit 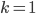 und der Menge
und der Menge 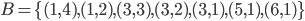 , welche aus
, welche aus 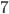 Tupeln besteht.
Tupeln besteht.
Wir haben also zwei Achsen, die wir wie in der Definition 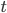 und
und  nennen. So sieht es dann aus:
nennen. So sieht es dann aus:
Das Bild ist angelehnt an das aus dem Skript, nur mit einer Sonne, die ich gleich erkläre. Im Skript steht
"Die Projektion ist der eindimensionale Schatten bei der Beleuchtung von oben".
Wir machen aus unserem 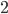 -Tupel nun ein
-Tupel nun ein  -Tupel: Uns interessieren nur die
-Tupel: Uns interessieren nur die  -Werte aus den Tupeln, und so kommen wir auf die 2. x-Achse im Bild für unser
-Werte aus den Tupeln, und so kommen wir auf die 2. x-Achse im Bild für unser 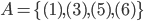 . Das ist unsere vorderste Front.
. Das ist unsere vorderste Front.
Der Projektionssatz sagt also aus:
War unsere Menge
rekursiv (entscheidbar), so ist unsere Projektion
rekursiv aufzählbar (r.a.). Die Umkehrrichtung gilt auch: Ist unsere Projektion r.a., so ist die Menge
entscheidbar.
Aber beweisen wie diese Aussagen zunächst:
1. Teilbeweis zu Nr. 1:  oder
oder  mit
mit  .
.
Das ist umgangssprachlich am besten so auszudrücken: eine leere Menge  ist der Definition nach immer rekursiv/entscheidbar. Also Auch immer rekursiv aufzählbar/semi-entscheidbar. Hier gibt es für uns nichts weiter zu beweisen.
ist der Definition nach immer rekursiv/entscheidbar. Also Auch immer rekursiv aufzählbar/semi-entscheidbar. Hier gibt es für uns nichts weiter zu beweisen.
Ansonsten gilt: wenn die Menge durch eine totale Funktion aufgezählt werden kann, so ist diese Menge rekursiv-aufzählbar/semi-entscheidbar. Das ist leicht einzusehen: Semi-Entscheidbarkeit einer Menge 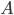 bedeutet ja, dass für für jedes Element aus
bedeutet ja, dass für für jedes Element aus 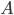 immer einen positiven (oder negativen, aber nicht beides gleichzeitig) Bescheid bekommen und somit auch
immer einen positiven (oder negativen, aber nicht beides gleichzeitig) Bescheid bekommen und somit auch 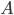 tatsächlich die Bildmenge der Funktion ist, die sie entscheidet: nämlich
tatsächlich die Bildmenge der Funktion ist, die sie entscheidet: nämlich 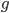 ist.
ist.
Haben wir z.B. die Gesamtmenge der Instanzen für das Post'sche Korrespondenzproblem und wollen wir daraus die Menge der lösbaren Instanzen konstruieren, so können wir für jedes Element der Gesamtmenge die Funktion 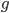 laufen lassen, die es in jedem Fall positiv entscheidet wenn eine Lösung dafür gefunden wurde (dass wir das können, haben wir im letzten Beitrag schon gezeigt) und somit jedes Element aus der Menge
laufen lassen, die es in jedem Fall positiv entscheidet wenn eine Lösung dafür gefunden wurde (dass wir das können, haben wir im letzten Beitrag schon gezeigt) und somit jedes Element aus der Menge 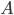 , der Menge der gelösten Probleminstanzen, aufzählen.
, der Menge der gelösten Probleminstanzen, aufzählen.
Genau diese Definition begründet den Namen Art von Mengen: sie werden von 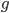 aufgezählt und sind damit rekursiv aufzählbar.
aufgezählt und sind damit rekursiv aufzählbar.
Das war der erste Teil. Kommen wir nun zum Umkehrschluss.
2. Teilbeweis zu Nr. 1:  oder
oder  mit
mit  .
.
Fall 1:  : Wir nehmen an, dass die
: Wir nehmen an, dass die 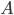 leer ist. Nun suchen wir eine Funktion
leer ist. Nun suchen wir eine Funktion 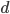 , die für alle Eingabewerte
, die für alle Eingabewerte 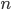 kein Ergebnis liefert und setzen
kein Ergebnis liefert und setzen 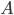 als Definitionsmenge dieser Funktion
als Definitionsmenge dieser Funktion 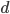 :
:  . Damit haben wir den ersten teil gezeigt.
. Damit haben wir den ersten teil gezeigt.
Fall 2: Nun nehmen wir eine totale Funktion 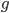 und setzen
und setzen 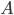 als Bildmenge von
als Bildmenge von 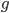 :
:  . Jetzt kommt unser
. Jetzt kommt unser 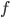 ins Spiel:
ins Spiel:
![f(y)=\mu{x}[g(x)=y]](https://fernuni.digreb.net/wp-content/plugins/latex/cache/tex_4811219128aa5dda453e1257ca60f93e.gif)
Was macht 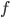 ? Es gibt uns für einen Eingabewert
? Es gibt uns für einen Eingabewert 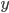 das kleinste
das kleinste  , wo gilt, dass der Funktionswert von
, wo gilt, dass der Funktionswert von 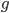 bei der Eingabe von
bei der Eingabe von  genau
genau 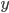 ist.
ist.
Man mache sich hier klar, dass egal, was 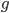 als Eingabewert bekommt, wir immer
als Eingabewert bekommt, wir immer 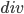 zurückbekommen (denn die leere Menge
zurückbekommen (denn die leere Menge 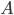 ist die Bildmenge von
ist die Bildmenge von 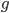 ).
).
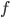 kann im Gegenzug alle Werte aus
kann im Gegenzug alle Werte aus 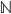 bekommen und auf alle abbilden. Diese Funktion ist offensichtlich berechenbar.
bekommen und auf alle abbilden. Diese Funktion ist offensichtlich berechenbar.
Das bedeutet: für ein  gibt es auch ein
gibt es auch ein  mit
mit  . Da
. Da  ist, gilt:
ist, gilt:  und
und  ist somit rekursiv aufzählbar.
ist somit rekursiv aufzählbar.
Und das war der zweite Teil.
1. Teilbeweis zu Nr. 2: 
Zeigen wir zunächst den umgekehrten Weg von Punkt 2 mit:  . Dafür gehen wir davon aus, dass eine Menge
. Dafür gehen wir davon aus, dass eine Menge  rekursiv aufzählbar ist:
rekursiv aufzählbar ist:
- Dann gibt es eine Gödelnummer
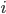 für ein
für ein  mit
mit  existiert.
existiert.
Es gibt also eine Maschine mit der Nr. 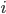 , die uns zum Element
, die uns zum Element  eine Ausgabe beschert. Die Cantorsche Tupelfunktion
eine Ausgabe beschert. Die Cantorsche Tupelfunktion 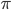 ist hier nur dazu da um eine evtl. Mehrstelligkeit
ist hier nur dazu da um eine evtl. Mehrstelligkeit 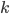 der Eingabe für die Maschine auf eine Stelle herunterzurechnen.
der Eingabe für die Maschine auf eine Stelle herunterzurechnen.
- Gibt es die Maschine mit der Nr.
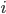 , so gibt es auch selbstverständlich die dazu gehörige Schrittzahlfunktion
, so gibt es auch selbstverständlich die dazu gehörige Schrittzahlfunktion  , die im
, die im 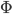 -Theorem benutzt wird:
-Theorem benutzt wird: 
Kennen wir alles schon: das ist die Anzahl der Schritte, die 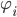 bei der Eingabe von
bei der Eingabe von  braucht um zum Ende zu gelangen. Da die Menge
braucht um zum Ende zu gelangen. Da die Menge 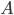 rekursiv aufzählbar ist, existiert für jedes
rekursiv aufzählbar ist, existiert für jedes  diese Rechenzeitfunktion
diese Rechenzeitfunktion 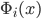 .
.
- Und damit gilt:

Es gibt also ein kleinstes 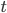 , d.h. die minimale Anzahl der Schritte, die die Maschine
, d.h. die minimale Anzahl der Schritte, die die Maschine 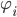 bei der Eingabe von
bei der Eingabe von  rechnet um bis zum Ergebnis zu gelangen. Es gibt aber auch noch mehr
rechnet um bis zum Ergebnis zu gelangen. Es gibt aber auch noch mehr  . Eben die, die kleiner sind als die maximale Schrittzahl, die die Maschine bei der Eingabe von
. Eben die, die kleiner sind als die maximale Schrittzahl, die die Maschine bei der Eingabe von  rechnet um bis zur HALT-Marke zu gelangen.
rechnet um bis zur HALT-Marke zu gelangen.
- Nun definieren wir die Menge

Die Paare sind also die Eingabe  für die Maschine
für die Maschine 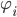 und
und 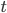 die Anzahl der Schritte, die die Maschine bis zum Ergebnis rechnen könnte. Sagen wir z.B. die Maschine rechnet bei der Eingabe von
die Anzahl der Schritte, die die Maschine bis zum Ergebnis rechnen könnte. Sagen wir z.B. die Maschine rechnet bei der Eingabe von  genau
genau 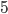 Schritte bis sie an der
Schritte bis sie an der 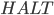 -Marke ankommt, so kann
-Marke ankommt, so kann  sein. In der Menge
sein. In der Menge 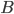 würde daher
würde daher  liegen.
liegen.
- Nach dem
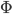 -Theorem ist diese Menge
-Theorem ist diese Menge 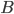 also entscheidbar.
also entscheidbar.
Das sollte klar sein: das Paar  , also die Eingabe
, also die Eingabe  und die Rechenzeit
und die Rechenzeit 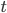 ist entscheidbar, da wir für jedes
ist entscheidbar, da wir für jedes  (wenn es in der Menge
(wenn es in der Menge 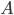 ist) immer einen Ausgabewert haben, ist auch die maximale Schrittzahl immer gegeben. Wir können entscheiden ob die Maschine bei der Eingabe von
ist) immer einen Ausgabewert haben, ist auch die maximale Schrittzahl immer gegeben. Wir können entscheiden ob die Maschine bei der Eingabe von  nach
nach 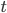 Schritten hält oder nicht.
Schritten hält oder nicht.
Anders ausgedrückt: Wir können fragen: "Hey, gilt  und
und 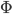 prüft ab ob bei der Eingabe von
prüft ab ob bei der Eingabe von  die Maschine innerhalb von
die Maschine innerhalb von 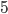 Schritten zum Ergebnis kommt und kann dann sagen "Ja, das geht!" oder "Nein, ging nicht!". Diese Menge ist also Entscheidbar.
Schritten zum Ergebnis kommt und kann dann sagen "Ja, das geht!" oder "Nein, ging nicht!". Diese Menge ist also Entscheidbar.
Der eine Weg von Punkt 2 ist damit gezeigt.
2. Teilbeweis zu Nr. 2: 
Und nun die andere Richtung:  . Sei
. Sei  also rekursiv/entscheidbar.
also rekursiv/entscheidbar.
- Setzen wir die Menge

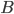 ist, wie wir wissen ja entscheidbar. Zu einer Eingabe erhalten wir (wenn sie zu einer r.a. Menge gehört) auch eine maximale Rechenzeit und können so prüfen ob sie
ist, wie wir wissen ja entscheidbar. Zu einer Eingabe erhalten wir (wenn sie zu einer r.a. Menge gehört) auch eine maximale Rechenzeit und können so prüfen ob sie 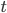 entspricht oder größer/kleiner ist. Hier ist
entspricht oder größer/kleiner ist. Hier ist 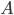 also die Menge der Eingaben, d.h. die ersten Elemente aus den Tupeln von
also die Menge der Eingaben, d.h. die ersten Elemente aus den Tupeln von 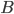 , die aus Eingabe
, die aus Eingabe  und zugehörigem Wert für eine angenommene Rechenzeit
und zugehörigem Wert für eine angenommene Rechenzeit 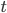 bestehen.
bestehen.
- Nun definieren wir unsere "Projektionsfunktion" durch
![f(x):=\mu{t}[cf_B(x,t)=1]](https://fernuni.digreb.net/wp-content/plugins/latex/cache/tex_11461119a7012f70895cb20b60072d4d.gif)
Was tut 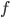 ? Zunächst fragen wir uns, was tut
? Zunächst fragen wir uns, was tut  ? Das ist die (volle) charakteristische Funktion für die Menge
? Das ist die (volle) charakteristische Funktion für die Menge 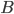 . Sie gibt uns eine
. Sie gibt uns eine  zurück wenn die Maschine bei der Eingabe von
zurück wenn die Maschine bei der Eingabe von  nach maximal
nach maximal 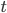 Schritten hält.
Schritten hält.
Und  ? Sie gibt uns das kleinste
? Sie gibt uns das kleinste 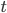 zurück, d.h. die minimalste Anzahl an Schritten, die benötigt werden um bei der Eingabe von
zurück, d.h. die minimalste Anzahl an Schritten, die benötigt werden um bei der Eingabe von  von der Maschine eine Ausgabe zu erhalten, denn in unserer menge
von der Maschine eine Ausgabe zu erhalten, denn in unserer menge 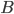 liegen ja durchaus mehrere Kombinationen von
liegen ja durchaus mehrere Kombinationen von  mit den unterschiedlichsten
mit den unterschiedlichsten  .
.
Mit 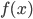 bekommen wir das also für die Eingabe
bekommen wir das also für die Eingabe  kleinste
kleinste 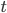 .
.
Der Definitionsbereich von 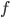 sind somit alle Elemente aus
sind somit alle Elemente aus 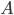 und
und 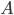 damit rekursiv aufzählbar.
damit rekursiv aufzählbar.
Done.
Exkurs: den Unterlagen der Uni Düsseldorf kann man den Projektionssatz auch mit einer anderen Menge 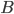 beweisen, z.B. mit
beweisen, z.B. mit  (wobei
(wobei  die Eingabe und
die Eingabe und  das durch die Tupelfunktion
das durch die Tupelfunktion 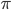 auf ein Element
auf ein Element 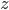 zurückgeführte Paar aus Ausgabe
zurückgeführte Paar aus Ausgabe 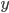 und Schrittzahl
und Schrittzahl 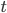 ist) wenn
ist) wenn  (auch Turingprädikat genannt) erfüllt ist.
(auch Turingprädikat genannt) erfüllt ist.
Das Turingprädikat ist genau dann erfüllt wenn Maschine 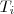 bei der Eingabe von
bei der Eingabe von  nach
nach 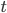 Schritten mit einer Ausgabe
Schritten mit einer Ausgabe 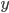 hält.
hält.
Im Endeffekt also nur ein kleines Upgrade unserer Menge 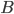 .
.
Fassen wir die Ergebnisse zusammen, kommen wir so zu unserer Antwort zum Lernziel.
Antwort zum Lernziel: Der erste Teil des Projektionssatzes ist der Grund für den Begriff "rekursiv-aufzählbar" für eine Menge 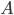 . Diese ist genau dann rekursiv-aufzählbar wenn ihre Elemente von einer totalen Funktion
. Diese ist genau dann rekursiv-aufzählbar wenn ihre Elemente von einer totalen Funktion 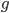 aufgezählt werden können, es gilt damit
aufgezählt werden können, es gilt damit  und
und 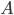 ist r.a.
ist r.a.
Der zweite Teil ist die Projektion, die aus den Eingabewerten  einer r.a. Menge
einer r.a. Menge 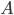 besteht. Da diese positiv beschieden sind, gibt es auch die zugehörige Anzahl an Schritten, die die Maschine für den positiven Bescheid brauchte. Setzen wir in den Tupeln
besteht. Da diese positiv beschieden sind, gibt es auch die zugehörige Anzahl an Schritten, die die Maschine für den positiven Bescheid brauchte. Setzen wir in den Tupeln  das Element
das Element 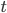 auf Werte, die höher sind als die Schrittzahlfunktion der Maschine bei der Eingabe
auf Werte, die höher sind als die Schrittzahlfunktion der Maschine bei der Eingabe  , so haben wir in der Menge
, so haben wir in der Menge 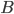 mehrere Tupel der Form
mehrere Tupel der Form  mit festem
mit festem  und variablem
und variablem 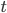 .
.
Aus diesen Elementen der Menge 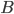 bilden wir die
bilden wir die  - und
- und 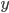 -Achse unserer Grafik. Diese Wertekombinationen aus
-Achse unserer Grafik. Diese Wertekombinationen aus  und
und 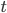 sind entscheidbar (ich kann entscheiden ob ich zu einer positiven Eingabe
sind entscheidbar (ich kann entscheiden ob ich zu einer positiven Eingabe  mehr als
mehr als 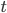 Schritte brauche oder nicht). Das ist der Weg von einer rekursiv-aufzählbaren Menge
Schritte brauche oder nicht). Das ist der Weg von einer rekursiv-aufzählbaren Menge 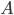 zu einer entscheidbaren
zu einer entscheidbaren 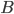 .
.
Auch der Rückweg gilt: aus der Menge 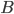 mit den Elementen
mit den Elementen  kann ich mir meine Eingabewerte
kann ich mir meine Eingabewerte  wieder rausholen, indem ich mich nur für das kleinste
wieder rausholen, indem ich mich nur für das kleinste 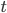 interessiere (die Minimierungsfunktion). Damit "blende" ich alle anderen Kombinationen mit größerem
interessiere (die Minimierungsfunktion). Damit "blende" ich alle anderen Kombinationen mit größerem 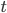 einfach aus. Das ist die Projektion.
einfach aus. Das ist die Projektion.
Merksatz: Eine Menge ist rekursiv aufzählbar wenn sie die Projektion einer entscheidbaren Menge ist.
Weiter geht es im nächsten Beitrag zum Halte- Äquivalenz- und Korrektheitsproblem, Reduzierbarkeit und Satz von Rice
Sie können zum Ende springen und ein Kommentar hinterlassen. Pingen ist im Augenblick nicht erlaubt.

Dezember 29th, 2013 00:16
Hi!
Erstmal vielen Dank für diese Seite! Du verstehst es wirklich zu ca 80 % das "Mathekauderwelsch" des Skriptes in verständlicher Art zu erklären. Aber das hier verstehe ich leider trotzdem noch nicht:
2. Teilbeweis zu Nr. 1 Fall 2.
Wo kommt auf einmal f her und wieso ist hier A auch die leere Menge? Weiteres wäre ja dann wenn für ganz g gilt Bild(g) = div , dass auch f nur div hervorbringt oder?