TIA: Rekursive und rekursiv-aufzählbare Mengen (Lernziele KE6, 1/4) (Update)
Update: Index-Fehler zu  (Danke, Martin!)
(Danke, Martin!)
Update: auch hier habe mich mich noch strikter an die Lernziele gehalten. Zusätzlich dazu wurden noch ein paar Beispiele zu entscheidbaren und semi-entscheidbaren Funktionen eingepflegt um das Verständnis zu erleichtern, was mir hoffentlich gelungen ist 😉
Update 2: ich merke gerade, dass die Einträge zu lang sind. Selbst die Ladezeiten vom Chrome sind bei den Mathe-Symbolen für 10 Seiten exorbitant hoch. Ich habe daher beschlossen die Beiträge daher zu trennen.
Es gibt insg. drei vier Beiträge zur KE6.
- TIA: Rekursive und rekursiv-aufzählbare Mengen (Lernziele KE6, 1/4)
- TIA: Bild- und Projektionssatz (Lernziele KE6 2/4)
- TIA: Halte- Äquivalenz- und Korrektheitsproblem, Reduzierbarkeit, Satz von Rice (Lernziele KE6, 3/4)
- TIA: Gödel'scher Unvollständigkeitssatz (Lernziele KE6, 4/4)
Da die Lernziele im Skript etwas verstreut sind, kann es sein, dass ich etwas springen muss und nicht alles der Reihe nach abhake. Lasst euch davon nicht verwirren.
Dieser Eintrag befasst sich mit rekursiven und rekursiv-aufzählbaren Mengen und ihren Eigenschaften. Wir hatten bereits in den anderen Beiträgen viel mit Mengen zu tun. Ich werde die Erklärungen hier einfach Copy&Pasten, falls sie passen.
Lernziel 1 und 3
Definition rekursiver und rekursiv aufzählbarer Mengen von Zahlen und Wörtern
Zunächst einmal hilft es sich wie Bart bei den Simpsons 100x "Rekursiv = entscheidbar. Rekursiv aufzählbar = Semi entscheidbar" wahlweise in das Parkett zu kratzen, die Wand zu tapezieren oder sich auf die Stirn tätowieren zu lassen. Nachdem das erledigt ist, wiederholt man das Gleiche dann noch mit der Definition (welche ich aus diesem Beitrag zur Entscheidbarkeit einfach Copy&Paste):
Eine Menge
ist entscheidbar/rekursiv wenn die charakteristische Funktion
definiert durch
berechenbar ist (Achtung: sie muss berechenbar sein und nicht einfach nur existieren!).
Achtung: die charakteristische Funktion existiert immer und ist im Falle der Entscheidbarkeit auch immer total!
Dann nochmal für r.a.:
Eine Menge
ist semi-entscheidbar/rekursiv aufzählbar wenn die partielle charakteristische Funktion
definiert durch
berechenbar ist.
Achtung: hier existiert die charakteristische Funktion ebenfalls, sie ist aber nicht mehr total!
Manchmal sagt man auch, dass die "halbe" charakteristische Funktion berechenbar ist. Oder wie im Skript ausgedrückt:
Eine Menge
ist semi-entscheidbar/rekursiv aufzählbar wenn es eine partielle berechenbare Funktion
gibt mit
.
Während sich die Definition für r.a. Mengen über die charakteristische Funktion noch erschließen mag, ist es bei dieser hier ein bisschen abstrakter.
Denkt euch eine Menge  , wo Ihr nur entscheiden könnt ob ein Element zu dieser Menge gehört, aber nicht ob es nicht dazu gehört (sie ist also offensichtlich nur semi-entscheidbar). Und nun lasst Ihr die charakteristische Funktion
, wo Ihr nur entscheiden könnt ob ein Element zu dieser Menge gehört, aber nicht ob es nicht dazu gehört (sie ist also offensichtlich nur semi-entscheidbar). Und nun lasst Ihr die charakteristische Funktion 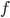 aus der 2. Definition auf jedem Element
aus der 2. Definition auf jedem Element 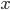 dieser Menge
dieser Menge  laufen.
laufen.
Gehört das Element 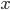 zu dieser Menge
zu dieser Menge  , so ist die Ausgabe der Funktion
, so ist die Ausgabe der Funktion  . Und das für jedes
. Und das für jedes  , dass zur Menge
, dass zur Menge  gehört. Gehört es nicht zur Menge
gehört. Gehört es nicht zur Menge  , so rechnet die Funktion unendlich lange weiter. Damit sind alle positiv entschiedenen Elemente
, so rechnet die Funktion unendlich lange weiter. Damit sind alle positiv entschiedenen Elemente  in der Menge
in der Menge  und ganz
und ganz  damit der Definitionsbereich der Funktion
damit der Definitionsbereich der Funktion 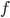 , eben
, eben  .
.
Wenn wir also entscheiden können ob ein Element in einer Menge ist oder nicht, ist die Menge rekursiv (z.B. bei der Entscheidung auf Primzahlen). Können wir nur positive (oder nur negative, aber nie beides) Entscheidungen treffen ob sich das Element in der Menge befindet (z.B. bei dem Halteproblem), dann ist die Menge nur rekursiv aufzählbar. Nicht vergessen: eine rekursive Menge ist auch rekursiv aufzählbar, aber eine rekursiv aufzählbare Menge nicht zwingend rekursiv.
Später kommen wir noch zu ein paar Beispielen für diese Mengen.
Eine weitere, wichtige Eigenschaft für rekursive Funktionen ist die folgende:
Eine unendliche Menge
ist rekursiv, gwd. es eine wachsende, totale Funktion
gibt mit
. Wachsend bedeutet:
Höre ich euch die Augenbrauen zusammenziehen? Müsst Ihr nicht. Es ist nicht schwer: was eine wachsende Funktion ist, wisst Ihr sicherlich: es ist eine Funktion, dessen Funktionswert bei der Eingabe vom Parameter 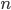 stets kleiner ist als bei der Eingabe von
stets kleiner ist als bei der Eingabe von  .
.
Beispiel: 
Stellen wir für  mal die Funktionswerte zusammen:
mal die Funktionswerte zusammen:

Kein Funktionswert von  ist kleiner als
ist kleiner als 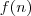 . Damit ist sie wachsend.
. Damit ist sie wachsend.
Schaffen wir es also so eine Funktion 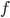 anzugeben, wo die Ausgabe (sog. Bildmenge) von
anzugeben, wo die Ausgabe (sog. Bildmenge) von 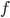 unsere komplette Menge
unsere komplette Menge  ist, so ist die Menge
ist, so ist die Menge  entscheidbar/rekursiv.
entscheidbar/rekursiv.
Exkurs Nr. 2: weiterhin sind alle endlichen Mengen rekursiv/entscheidbar. Warum? Nehmen wir einfach eine beliebige, endliche Menge  . Egal welche Eigenschaften wir dieser Menge zuordnen, so können wir (theoretisch) einfach eine riesige charakteristische Funktion angeben, die für jedes Element entscheidet ob es zu
. Egal welche Eigenschaften wir dieser Menge zuordnen, so können wir (theoretisch) einfach eine riesige charakteristische Funktion angeben, die für jedes Element entscheidet ob es zu  gehört oder nicht. Denn die Menge ist endlich.
gehört oder nicht. Denn die Menge ist endlich.
Nun solltet Ihr einen kleinen Eindruck davon bekommen haben was entscheidbar/rekursiv und was semi-entscheidbar/rekursiv-aufzählbar ist.
Exkurs Nr. 3: Zusammenhang zu Wörtern
Der Zusammenhang zwischen Zahlen und Wörtern sollte nach der Standardnummerierung 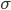 der Wörter über
der Wörter über 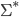 sollte euch bereits klar sein. Denn alles, was wir über Mengen auf
sollte euch bereits klar sein. Denn alles, was wir über Mengen auf  oder
oder 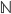 aufzählen, gilt selbstverständlich auch für Mengen über einem Alphabet
aufzählen, gilt selbstverständlich auch für Mengen über einem Alphabet 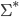 .
.
Mittels Standardnummerierung können wir Worte aus einem Alphabet 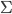 nummerieren und umgekehrt. Das haben wir im Beitrag über
nummerieren und umgekehrt. Das haben wir im Beitrag über 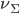 bereits erfolgreich getan.
bereits erfolgreich getan.
Ebenfalls konnten wir Bandprogramme 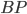 erfolgreich mit
erfolgreich mit  nummerieren und entscheiden ob ein Wort über dem "Programmiersprachenalphabet"
nummerieren und entscheiden ob ein Wort über dem "Programmiersprachenalphabet"  ein Bandprogramm ist oder nicht. Damit ist die Menge der Bandprogramme
ein Bandprogramm ist oder nicht. Damit ist die Menge der Bandprogramme 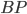 , der PASCAL-Programme und die Menge der
, der PASCAL-Programme und die Menge der  -Programme entscheidbar/rekursiv.
-Programme entscheidbar/rekursiv.
Antwort zum Lernziel: eine Menge ist rekursiv/entscheidbar wenn ihre (volle) charakteristische Funktion berechenbar ist. Für eine nur semi-entscheidbare/rekursiv-aufzählbare Menge muss nur die "halbe" charakteristische Funktion berechenbar sein.
Im ersten Fall können wir damit die vollständige Menge  entscheiden, d.h. ob ein Element zu dieser gehört oder nicht (formal ausgedrückt:
entscheiden, d.h. ob ein Element zu dieser gehört oder nicht (formal ausgedrückt:  und
und  ). Im letzten Fall können wir nur positiv oder negativ entscheiden, aber nie beides gleichzeitig (formal ausgedrückt:
). Im letzten Fall können wir nur positiv oder negativ entscheiden, aber nie beides gleichzeitig (formal ausgedrückt:  oder
oder  , aber nicht beides gleichzeitig).
, aber nicht beides gleichzeitig).
Eine Art Ausnahme bildet das Komplement einer semi-entscheidbaren Menge: können wir dieses ebenfalls semi-entscheiden, so ist die komplette Menge entscheidbar. Denn damit haben wir im Endeffekt die positive und negative Antwort, d.h. die "volle" charakteristische Funktion berechnet.
Lernziel 4
Abschlusseigenschaften rekursiver und rekursiv aufzählbarer Mengen
Im Skript werden die folgenden, abschließenden Eigenschaften von rekursiven/entscheidbaren Mengen genannt:
1.
rekursiv. Damit ist auch
und
rekursiv.
2. Sei
rekursiv, sei
. Dann ist
rekursiv.
3. Sei
, dann gilt:
rekursiv
rekursiv.
Die 1. Eigenschaft ist soweit deutlich: 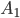 und
und 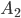 sind Teilmengen aus
sind Teilmengen aus  mit eben der Stelligkeit
mit eben der Stelligkeit 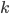 . Restmenge, Vereinigungsmenge und Schnittmenge sind damit auch rekursiv.
. Restmenge, Vereinigungsmenge und Schnittmenge sind damit auch rekursiv.
Eigenschaft Nr. 2 ist etwas aufwändiger wenn Ihr mit der Schreibweise nicht vertraut seid und (wie ich) Abschnitt 1.3 überlesen habt. Daher hier zur Auffrischung nochmal. Einer Korrespondenz wird eine Funktion 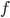 zugeordnet, die Mengen transformiert. Die Umkehrfunktion davon
zugeordnet, die Mengen transformiert. Die Umkehrfunktion davon ![f^{-1}[A]](https://fernuni.digreb.net/wp-content/plugins/latex/cache/tex_303907c9398300fafffc1ef83cf1829f.gif) . Wenn die Menge
. Wenn die Menge  nun rekursiv ist und es eine totale Funktion
nun rekursiv ist und es eine totale Funktion 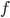 gibt, so ist auch die Umkehrfunktion rekursiv.
gibt, so ist auch die Umkehrfunktion rekursiv.
Durch die Cantorfunktion aus Eigenschaft Nr. 3 können wir uns bei unseren Untersuchungen auf die rekursiven Teilmengen von 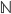 beschränken. Wir erinnern uns: wie können mit dieser Funktion
beschränken. Wir erinnern uns: wie können mit dieser Funktion 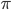 beliebige
beliebige 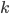 -stellige Tupel auf eine natürliche Zahl aus
-stellige Tupel auf eine natürliche Zahl aus 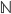 abbilden. Wer sich nicht dran erinnert, sollte sich nochmal den Beitrag zu Gemüte führen.
abbilden. Wer sich nicht dran erinnert, sollte sich nochmal den Beitrag zu Gemüte führen.
Wir haben damit sichergestellt, dass Operatoren die rekursiven Mengen auch wieder in rekursive Mengen transformieren.
Anschließend folgen die Abschlusseigenschaften der rekursiv aufzählbaren/semi-entscheidbaren (r.a.) Mengen:
1.
r.a. Damit ist auch
und
r.a.
2. Sei
r.a., sei
. Dann ist
r.a.
3. Sei
, dann gilt:
r.a.
r.a.
Die Erläuterung erfolgt analog zu rekursiven Mengen. Bitte aber beachten, dass wir nun auf den partiellen, mehrstelligen, berechenbaren Funktionen  arbeiten und nicht mehr auf den totalen
arbeiten und nicht mehr auf den totalen  .
.
Zusammenfassend zitiere ich aus der Wikipedia für die rekursiven/entscheidbaren und rekursiv-aufzählbare/semi-entscheidbare Mengen:
- Jede entscheidbare Menge ist rekursiv aufzählbar, aber es gibt rekursiv aufzählbare Mengen, die nicht entscheidbar sind.
- Eine Menge ist genau dann entscheidbar, wenn sie und ihr Komplement rekursiv aufzählbar sind.
- Jede endliche Menge ist rekursiv aufzählbar.
- Jede rekursiv aufzählbare Menge ist abzählbar, aber nicht alle abzählbaren Mengen sind rekursiv aufzählbar.
- Jede unendliche rekursiv aufzählbare Menge besitzt Teilmengen, die nicht rekursiv aufzählbar sind.
- Der Schnitt von endlich vielen rekursiv aufzählbaren Mengen ist rekursiv aufzählbar; die Vereinigung einer rekursiv aufzählbaren Menge von rekursiv aufzählbaren Mengen ist rekursiv aufzählbar. Es gibt rekursiv aufzählbaren Mengen, deren Komplement nicht rekursiv aufzählbar ist.
Antwort zum Lernziel: die entscheidbaren Mengen sind abgeschlossen bzgl. Komplement, Schnitt und Vereinigung. Die semi-entscheidbaren mengen jedoch nur bzgl. Schnitt und Vereinigung, das Komplement ist nicht semi-entscheidbar (wäre es das, so wäre die Menge vollständig entscheidbar. Siehe vorheriges Lernziel).
Lernziel 2a
Nachweis der Rekursivität/Entscheidbarkeit von Mengen
Was tun wir um die Rekursivität von Mengen zu beweisen? Wir geben ein Flussdiagramm einer verallgemeinerten Registermaschine an, welches die charakteristische Funktion für die zu untersuchende Menge berechnet. Wir entscheiden nun wirklich ob ein Element in der rekursiven Menge ist oder nicht. Dazu verwenden wir alle bereits als berechenbar bewiesenen Funktionen. Mehr nicht.
Hilfreich ist hierfür die Auflistung der berechenbaren Funktionen aus Satz 3.2.5:
- Nullfunktion
- Nachfolger- und Vorgängerfunktion
- Projektion
- konstante Funktion
- Summe
- arithmetische Differenz
- Produkt
- Quotient und Rest
- Exponentation
- Wurzel
- max/min
- Primzahltest und
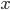 -te Primzahl
-te Primzahl
Könnt ihr alle für euer Flussdiagramm benutzen 😉
Beispiel? Sicher: 
Die dazu notwendige, charakteristische Funktion ist:

Test auf Primzahl: Für alle 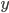 mit
mit  wird getestet ob es bei der Division von
wird getestet ob es bei der Division von 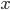 durch
durch 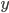 einen Rest gibt. Gibt es bei einem
einen Rest gibt. Gibt es bei einem 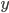 keinen Rest, so ist es keine Primzahl (dann ist
keinen Rest, so ist es keine Primzahl (dann ist 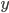 nämlich ein legitimer Teiler von
nämlich ein legitimer Teiler von 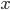 ).
).
Damit können wir für jedes  entscheiden ob es eine Primzahl ist oder nicht. Das Flussdiagramm für den Test dürft Ihr selbst angeben 😉
entscheiden ob es eine Primzahl ist oder nicht. Das Flussdiagramm für den Test dürft Ihr selbst angeben 😉
Ein weiteres Beispiel wäre z.B. der Test auf die Goldbach-Eigenschaft einer Zahl.
Antwort zum Lernziel: um zu zeigen, dass eine Menge entscheidbar/rekursiv ist, muss die (volle) charakteristische Funktion berechenbar sein.
Dazu gibt man das Flussdiagramm einer verallgemeinerten Maschine (wenn man streng ist, muss man für jeden verallgemeinerten Test seine Berechenbarkeit ebenfalls nachweisen und letztendlich seine Maschine auf die drei Grundoperationen Addition/Subtraktion von  und Test auf
und Test auf 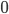 zurückführen) an, die diese berechnet und in jedem Fall mit einem Ergebnis hält.
zurückführen) an, die diese berechnet und in jedem Fall mit einem Ergebnis hält.
Lernziel 2b
Nachweis der rekursiven Aufzählbarkeit/Semi-entscheidbarkeit von Mengen
Auch hier ist es nicht allzu schwierig. Jede rekursiv aufzählbare (semi entscheidbare) Menge ist auch gleichzeitig aufzählbar und jede aufzählbare Menge ist auch rekursiv aufzählbar (semi entscheidbar). Daher müssen wir es nur schaffen, die Elemente der Menge irgendwie aufzuzählen. Man macht sich leicht klar, dass der Definitionsbereich und Wertebereich von berechenbaren Funktionen rekursiv aufzählbar ist.
Aber was ist mit 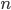 -Tupeln? Die sind dank Cantor'schen Tupelfunktion auf ein Element reduzierbar, d.h. wir können
-Tupeln? Die sind dank Cantor'schen Tupelfunktion auf ein Element reduzierbar, d.h. wir können 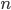 -Tupel auf einelementige Mengen reduzieren und unseren Schabernack mit ihnen treiben.
-Tupel auf einelementige Mengen reduzieren und unseren Schabernack mit ihnen treiben.
Wird also gefragt, ob eine Menge rekursiv aufzählbar ist, so geben wir einfach eine charakteristische Funktion an, die die Eigenschaft der Menge nur positiv (oder nur negativ) beantwortet. Für die gegensätzliche Antwort muss unsere charakteristische Funktion (im Gegensatz zur vollen charakteristischen Funktion für entscheidbare Mengen) nicht halten, Hauptsache sie sagt uns zuverlässig eine der beiden Antworten. Ein gutes Beispiel ist das Post'sche Korrespondenzproblem.
Beispiel: Post'sches Korrespondenzproblem
Das Post'sche Korrespondenzproblem beschreibt das Problem bei Wortpaaren 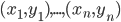 eine Folge
eine Folge 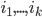 mit der Eigenschaft:
mit der Eigenschaft: 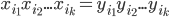 zu finden. Ist natürlich wieder etwas abstrakt, aber probieren wir das mal an einem Beispielproblem:
zu finden. Ist natürlich wieder etwas abstrakt, aber probieren wir das mal an einem Beispielproblem:
Beispielproblem 
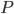 nennt man Problemfall oder Instanz.
nennt man Problemfall oder Instanz.
Fragestellung: gibt es eine Lösung (d.h. eine Folge von Indices) 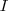 zum Problemfall
zum Problemfall 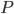 ? Wenn ja, ist die Folge eine Lösung von
? Wenn ja, ist die Folge eine Lösung von 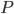 .
.
Wir müssen hier also eine Kombination von zwei Wortkombinationen 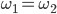 finden und die folgenden Regeln einhalten:
finden und die folgenden Regeln einhalten:
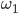 darf nur aus den 1. Elementen der 3 Wortpaare bestehen:
darf nur aus den 1. Elementen der 3 Wortpaare bestehen: 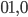 und
und 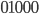 .
.- Das Wort
 darf nur aus den 2. Elementen der 3 Wortpaare bestehen:
darf nur aus den 2. Elementen der 3 Wortpaare bestehen: 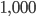 und
und 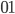 .
. - Die Wortkombinationen
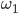 und
und 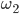 dürfen beliebig lang sein.
dürfen beliebig lang sein.
Was Indices sind, ist euch klar? Nein, keine Sorge. Kommt gleich. Es liegt also an unserer Kombinationsgabe eine passende Index-Kombination zu finden, so dass am Ende gilt:  .
.
Eine mögliche Lösung wäre  und
und  . (die
. (die  sind nur optische Trennzeichen damit Ihr die Elemente identifizieren könnt aus denen die Worte bestehen).
sind nur optische Trennzeichen damit Ihr die Elemente identifizieren könnt aus denen die Worte bestehen).
Die zugehörigen Indices wären: 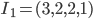 . Damit ist
. Damit ist  eine Lösung für
eine Lösung für 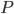 und
und 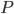 damit gelöst.
damit gelöst.
Die Indices sind nichts weiter als die Nummer des Tupels, dass zur Bildung herangezogen wird. Da wir für das erste Wort 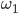 nur die ersten und für das zweite Wort
nur die ersten und für das zweite Wort 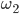 nur die zweiten Elemente aus den Tupeln benutzen dürfen, reicht uns als Angabe einfach nur die Nummer des Tupels.
nur die zweiten Elemente aus den Tupeln benutzen dürfen, reicht uns als Angabe einfach nur die Nummer des Tupels.
Würden wir z.B. die folgende Lösung austesten wollen:  , so wären die Worte
, so wären die Worte 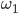 und
und 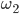 :
:
 und
und

Da  , ist die mögliche Lösung
, ist die mögliche Lösung 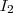 falsch und
falsch und 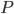 noch nicht gelöst. Aber was nicht ist, kann ja noch werden!
noch nicht gelöst. Aber was nicht ist, kann ja noch werden!
Um zu zeigen, dass die Menge dieser Worttupel rekursiv aufzählbar/semi entscheidbar ist brauchen wir nur zu zeigen, dass die Menge der Definitionsbereich einer partiellen Funktion ist und die dazugehörige Maschine anzugeben, welche die charakteristische Funktion für diese Menge berechnet und in jedem Fall mit einer  terminiert wenn das Element in der Menge ist oder nicht terminiert, wenn es das nicht ist.
terminiert wenn das Element in der Menge ist oder nicht terminiert, wenn es das nicht ist.
Die charakteristische Funktion für dieses Problem wäre:

Das Flussdiagramm beschreibe ich hier ebenfalls am besten in Pseudocode:
- Setze

- Fange mit einer Indexfolge
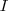 der Länge
der Länge 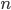 an
an - Erstelle durch den Index
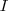 die Worte
die Worte 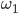 und
und 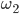 mit Länge
mit Länge 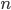
- Prüfe ob
 .
.
Wenn ja, so ist eine Lösung für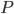 gefunden: HALT!
gefunden: HALT!
Wenn nein, setze und gehe zu Punkt 2.
und gehe zu Punkt 2.
Wie man am Pseudocode gut erkennen kann, kann man zu einer gegebenen Probleminstanz 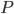 eine Lösung durch systematisches ausprobieren finden.
eine Lösung durch systematisches ausprobieren finden.
Es ist damit sichergestellt, dass wir so tatsächlich eine korrekte Lösung finden wenn es eine gibt. Und wenn nicht? Da die Länge der Indexfolge unendlich ist und unsere Worte somit unendlich lang werden, kann es sein, dass wir niemals anhalten. Im ungünstigsten Fall läuft unser Programm für eine Kombination also ewig.
So können wir nur schlussfolgern ob eine konkrete Belegung von 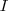 eine Lösung darstellt oder nicht. Aber wir werden nie wissen ob
eine Lösung darstellt oder nicht. Aber wir werden nie wissen ob 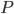 nicht doch vielleicht eine Lösung hat.
nicht doch vielleicht eine Lösung hat.
Kleiner Exkurs: Tatsächlich können wir das Problem für eine kleine Anzahl an Paaren wirklich entscheiden (für ein oder zwei Paare ist das Problem nach Ehrenfeucht und Rozenberg (1981) entscheidbar)! Für die Anzahl zwischen zwei und drei Paaren ist es noch nicht ganz geklärt, während die Anzahl von sieben paaren bereits ausreicht um von Unentscheidbarkeit zu sprechen (Matiyasevich, 1996).
Noch ein Exkurs: Eine weitere Möglichkeit zu zeigen, dass das Post'sche Korrespondenzproblem nicht entscheidbar ist die Reduktion einer nicht entscheidbaren Menge auf dieses. Aber zum Thema Reduktion kommen wir noch in Teil B der theoretischen Informatik.
Antwort zum Lernziel: Um zu zeigen, dass eine Menge semi-entscheidbar/rekursiv-aufzählbar ist, muss die "halbe" charakteristische Funktion berechenbar sein. Wir müssen also mit Gewissheit sagen können, ob ein Element zur Menge gehört. Das Gegenteil ist uns hier aber vergönnt und wir nehmen es in Kauf, dass unsere Testmaschine für eine Eingabe im ungünstigsten Fall ewig rechnet.
Dazu gibt muss man ebenfalls man das Flussdiagramm einer verallgemeinerten Maschine angeben, aus der ersichtlich ist, dass sie eine Eingabe in jedem Fall positiv bewertet wenn es denn eine Lösung zum gestellten Problem ist und so lange weiterrechnet bis eine Lösung gefunden ist. Im schlimmsten Fall eben ewig.
Lernziel 6
Erläuterung des Zusammenhangs zwischen rekursiven und rekursiv-aufzählbaren Mengen
Eine spannende, aber offensichtliche Beziehung zwischen entscheidbaren und semi-entscheidbaren Mengen ist: eine Menge ist entscheidbar wenn die Menge selbst und ihr Komplement semi-entscheidbar sind. Formal ausgedrückt:
Eine Menge
ist rekursiv, gdw.
und
r.a. sind.
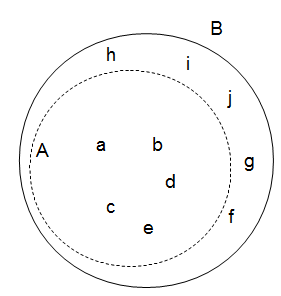
Nehmen wir also an, wir haben eine semi-entscheidbare Menge  . Wie wir wissen, ist sie semi-entscheidbar, d.h. wir können entscheiden ob ein Element zu dieser Menge gehört. Aber nicht das Gegenteil.
. Wie wir wissen, ist sie semi-entscheidbar, d.h. wir können entscheiden ob ein Element zu dieser Menge gehört. Aber nicht das Gegenteil.
Und was wäre dann die Menge  ? In dieser Menge wären genau die Elemente, die zwar aus
? In dieser Menge wären genau die Elemente, die zwar aus 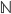 sind, sich aber nicht in
sind, sich aber nicht in  befinden.
befinden.
Im Endeffekt haben wir so quasi zwei "halbe" charakteristische Funktionen, die jeweils einen Teil entscheiden, welchen die andere charakteristische Funktion nicht entschieden hat. Beide zusammen bilden dann eine "volle" charakteristische Funktion für  .
.
Beispiel: 
Wir können also die Menge  semi-entscheiden. Ob ein Element nicht in der Menge
semi-entscheiden. Ob ein Element nicht in der Menge  ist hingegen nicht.
ist hingegen nicht.
Und was wäre wenn wir das Komplement  entscheiden könnten? Also nur die Elemente
entscheiden könnten? Also nur die Elemente  ? Dann könnten wir für alle Elemente aus
? Dann könnten wir für alle Elemente aus  sagen, ob sie zu Menge
sagen, ob sie zu Menge  gehören und für den Rest bestimmen ob sie zu
gehören und für den Rest bestimmen ob sie zu  gehören. Damit würde für jedes Element eine positive und negative Entscheidung gefällt werden könne.
gehören. Damit würde für jedes Element eine positive und negative Entscheidung gefällt werden könne.
Und wenn das der Fall ist, ist  was? Genau! Komplett entscheidbar/rekursiv.
was? Genau! Komplett entscheidbar/rekursiv.
Die charakteristische Funktion 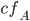 für
für  wäre also:
wäre also:
Fertig. Damit ist die Menge  (und natürlich auch
(und natürlich auch 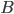 ) rekursiv/entscheidbar.
) rekursiv/entscheidbar.
Antwort zum Lernziel: Ist es uns möglich die Teilmenge einer anderen Menge  positiv (aber nicht negativ) zu entscheiden, so ist diese semi-entscheidbar. Können wir für den Rest, d.h. die Menge ohne die bereits positiv entschiedene Menge
positiv (aber nicht negativ) zu entscheiden, so ist diese semi-entscheidbar. Können wir für den Rest, d.h. die Menge ohne die bereits positiv entschiedene Menge  ebenfalls entscheiden, so ist die gesamte Menge
ebenfalls entscheiden, so ist die gesamte Menge  damit rekursiv/entscheidbar.
damit rekursiv/entscheidbar.
Weiter geht es mit den nächsten Lernzielen im Beitrag zum Bild- und Projektionssatz.
Bei Fehlern gilt wie immer: ASAP in die Kommentare damit.
Sie können zum Ende springen und ein Kommentar hinterlassen. Pingen ist im Augenblick nicht erlaubt.

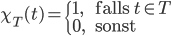
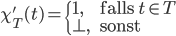

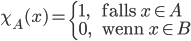
März 25th, 2015 15:28
Hi!
Sollte die Lösung $I_1$ zum Problem $P$ nicht $I = ( 3, 2, 2, 1 )$ lauten? Oder hab ich es nur nicht verstanden?
Beste Grüße
März 25th, 2015 15:42
Du hast Recht, ist behoben. Danke.