Zusammenfassungen: Theoretische Informatik
Hier findet Ihr meine Zusammenfassungen und Erläuterungen zur theoretischen Informatik (01657 und 01658).
Diese Zusammenfassungen hier habe ich eig. nur für mich erstellt und habe sie später einigen Kommilitonen zur Verfügung gestellt um ihnen etwas Zeit zu sparen, da der Stoff in der dargestellten Form doch eher schwer verdaulich ist. Außerdem gibt es ein Problem mit der Sekundärliteratur, da bestimmte Dinge im Skript einfach anders definiert sind. Sie sind zwar dennoch korrekt, aber auch bestimmten Gründen besteht im Skript z.B. etwas aus einem 4-Tupel und in der Literatur aus einem 5-Tupel, usw.
Da die Zusammenfassungen den Mitstudenten anscheinend ganz gut beim Verständnis der Materie halfen (wenn ich der positiven Resonanz glauben darf), habe ich beschlossen sie online zu stellen. Vielleicht helfen sie euch auch.
Thema Copyright
Die Fragestellungen und einige Inhalte stammen aus dem Skript der FernUni Hagen, das Copyright liegt also dort. Stellen, die ich aus dem Buch von Dirk W. Hoffmann oder Rolf Socher entnommen habe sind ebenfalls markiert. Ich habe mich bemüht alle Bilder selbst zu erstellen, nur CC--Bilder zu verwenden oder mindestens die Quelle zu nennen. Wenn irgendwo was fehlt oder ich euer Bild verwendet haben sollte, was ihr nicht wollt, bitte ich um eine kurze Mail an mich. Ich entferne es direkt.
Ganz wichtig
Auch wenn ich die Zusammenfassungen nach bestem Wissen und Gewissen angefertigt habe, gibt es sicherlich noch irgendwo den ein oder anderen Fehler. Aber nichts stört den Lernprozess so wie diese. Erklärungen werden nicht nachvollziehbar wenn man nicht auf das selbe Ergebnis kommt wie der Autor. Sollten euch daher grobe Schnitzer auffallen, bitte sofort per Mail oder in den Kommentaren melden. Danke!
Behaltet aber eines im Hinterkopf:
Auch sollten die Zusammenfassungen höchstens ergänzend zum Skript verwendet werden wenn Ihr mal eine andere Sicht auf die Dinge braucht weil ihr im Skript nicht weiterkommt. Nur das Skript ist wirklich verbindlich!
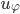 ist berechenbar...", dann ist die Aussage "Es gibt eine Funktion
ist berechenbar...", dann ist die Aussage "Es gibt eine Funktion 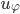 ..." schlicht falsch. Dass Ihr aber im Detail erklären könnt, was
..." schlicht falsch. Dass Ihr aber im Detail erklären könnt, was 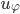 macht nützt euch ab hier nicht mehr viel, die gegebene Antwort war nicht richtig und 0 Punkte wert.
macht nützt euch ab hier nicht mehr viel, die gegebene Antwort war nicht richtig und 0 Punkte wert.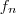 ist eine partielle Funktion...", so ist eine Antwort mit "
ist eine partielle Funktion...", so ist eine Antwort mit "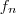 ist eine Funktion..." falsch und ihr kommt noch nicht einmal dazu, zu erläutern was sie tut warum sie partiell ist. Selbst wenn Ihr es wisst.
ist eine Funktion..." falsch und ihr kommt noch nicht einmal dazu, zu erläutern was sie tut warum sie partiell ist. Selbst wenn Ihr es wisst.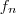 ist eine Funktion..." ist eine falsche Antwort.
ist eine Funktion..." ist eine falsche Antwort.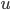 in
in 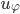 , ...) eine Rolle.
, ...) eine Rolle.PS: Ihr merkt aus den obigen Zeilen, dass ich mit der Prüfung nicht so ganz zufrieden war. Ich habe bestanden. Aber nicht so gut, wie ich das gerne hätte und wie das dem Aufwand, den ich betrieben habe entsprechen würde.
Das lag aber nicht am Prof., sondern einfach an der Tatsache, dass ich mich habe von dem Gedanken leiten lassen, das Verständnis der Materie und der Zusammenhänge würde ausreichen. Denn darum ginge es ja letztendlich: etwas zu verstehen. Die genauen Definitionen seien etwas, was man zur Not würde nachschlagen können. Das ist leider nicht richtig. Bestimmte Dinge müssen einfach "sitzen" und exakt formuliert werden können.
Hätte ich das vorher gewusst, hätte ich mich anders vorbereitet. Mehr im Stil von BGB als im Stil von Software Engineering.
Das hat aber nichts mit dem Prof. oder der Prüfung zu tun. Diese ist fair, der Prof. sehr nett und die Benotung wohlwollend. Macht euch also darüber keine Gedanken. Lernt aber nicht nur für das Verständnis der Materie, sondern lernt auch, euch mathematisch präzise genug auszudrücken um die wichtigen Definitionen ohne Füllwörter oder Ungenauigkeiten benennen zu können.
Ich weiß, dass genau dies ein Problem bei einem Fernstudium ist. Denn das höchste der Gefühle ist, dass man gelegentlich mit den Mitstudenten skyped oder sich auch mal in der Lerngruppe trifft. Das reicht aber leider nicht, denn i.d.R. ist der Mitstudent auch nicht so tief in der Materie drin, dass er Ungenauigkeiten direkt erkennt und euch darauf hinweist. Man spricht darüber, erklärt es einander und gut ist's. Das ist aber nicht genug.
Daher nehmt auch, selbst wenn ihr meint alles verstanden zu haben, die Gelegenheit wahr an den Studientagen oder den Mentoriaten teilzunehmen, bearbeitet die Einsendeaufgaben so gut es halt geht und schreibt die Leistungsnachweise. Nutzt jede Gelegenheit um euch in Genauigkeit zu üben. Es geht hier schließlich um Mathematik und nicht um Politik 😉
Zusammenfassungen theoretische Informatik A (01657)
Kurseinheit 1
Die erste Kurseinheit der theoretischen Informatik A beginnt mit Flussdiagrammen, Einzelschritt-, Schrittzahl- und Gesamtschrittfunktionen und ihrer Semantik. Anschließend geht es von Maschinen über Registermaschinen mit nur drei Grundoperationen zu verallgemeinerten Registermaschinen mit komplexeren Möglichkeiten.
Diese nutzen wir um zu beweisen, dass Zahlenfunktionen berechenbar sind und weisen das anhand einiger Beispiele auch mittels vollständiger Induktion über die Einzelschrittfunktion nach.
TIA: Flussdiagramme, Registermaschinen und berechenbare Zahlenfunktionen (Lernziele KE1)
- Angabe und Erläuterung der Definition des Flussdiagramms
- Angabe und Erläuterung der Semantik des Flussdiagramms
- Angabe und Erläuterung der Definition und Semantik einer Maschine
- Angabe und Erläuterung der Definition einer Registermaschine
- Angabe und Erläuterung der Definition einer verallgemeinerten Registermaschine
- Angabe der Definition einer berechenbaren Zahlenfunktion
- Zeigen, dass eine Funktion berechenbar ist
Kurseinheit 2
In der zweiten Kurseinheit gibt es zwar nur drei Lernziele und das Skript ist im Umfang her ziemlich dünn, aber es werden tatsächlich essentielle Dinge angesprochen. Für mein Empfinden auch etwas zu schnell abgehandelt. In Sekundärliteratur widmen die Autoren diesen Themen eigene Kapitel.
Die behandelten Themen sind: die Cantorsche Tupelfunktion (auch Paarungsfunktion genannt), sowie einige Eigenschaften berechenbarer Zahlenfunktionen und die damit zusammenhängende primitive- und 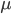 -Rekursion, die uns die
-Rekursion, die uns die  -und
-und  -Berechenbarkeit mathematisch abbilden.
-Berechenbarkeit mathematisch abbilden.
TIA: Berechenbare Zahlenfunktionen (Lernziele KE2)
- Angabe und Erläuterung der Definition und der Eigenschaften der Cantorschen Tupelfunktion
- Erläuterung der Abschlusseigenschaften berechenbarer Zahlenfunktionen
- Definition der WHILE-Programme, Erläuterung ihrer Semantik und Angabe des Zusammenhangs zu berechenbaren Funktionen
Kurseinheit 3
Das Thema dieser Kurseinheit sind Turingmaschinen. Einband-, Mehrbandmaschinen und wie sie ineinander überführt werden können.
In diesem Kontext treffen wir auch die Hilfssymbole zur Simulation der Kopfpositionen von Mehrbandmaschinen und wie wir sie eliminieren um das Arbeitsalphabet (Bandalphabet) nicht unnötig aufblähen zu müssen.
Weiterhin beweisen wir hier die Berechenbarkeit einfacher Wortfunktionen mittels vollständiger Induktion über die Turingmaschinen nach.
TIA: Turingmaschinen, Bandmaschinen und berechenbare Wortfunktionen (Lernziele KE3)
- Erläuterung der Definition einer Turingmaschine
- Nachweis der Berechenbarkeit einfacher Wortfunktionen
- Erläuterung der Definition einer Bandmaschine
- Erläuterung der Grundidee des Beweises Turing-berechenbar = Band-berechenbar
- Erläuterung der Grundidee des Beweises, dass man bei Bandmaschinen ohne Hilfssymbole auskommt
Kurseinheit 4
Diese Kurseinheit ist etwas dicker als die anderen. Bzw. sollte sie sein, da doch einige essentielle Themen wie  - und
- und  -Berechenbarkeit angesprochen werden. Leider sind die entsprechenden Kapitel im Skript nur knapp gehalten, während sie in anderer Literatur ein paar Seiten mehr umfassen.
-Berechenbarkeit angesprochen werden. Leider sind die entsprechenden Kapitel im Skript nur knapp gehalten, während sie in anderer Literatur ein paar Seiten mehr umfassen.
Behandelte Themen sind die folgenden: Standardnummerierung und die dadurch induzierte Beziehung zwischen Zahlen und Wortfunktionen,  -Berechenbarkeit und damit die primitiv-rekursiven Funktionen, die
-Berechenbarkeit und damit die primitiv-rekursiven Funktionen, die  -Berechenbarkeit und die
-Berechenbarkeit und die 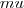 -rekursiven Funktionen, Churchsche These und erste Erwähnung der Beweisverfahren mittels Diagonalisierung (Cantor).
-rekursiven Funktionen, Churchsche These und erste Erwähnung der Beweisverfahren mittels Diagonalisierung (Cantor).
TIA: Berechenbarkeit (Kernziele KE4)
- Angabe und Erläuterung der Definition einer Standardnummerierung von
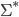
- Formulierung und Erläuterung der Beziehung zwischen Zahlen- und Wortfunktionen
- Definition der primitiv-rekursiven Funktionen
- Beweis, dass bestimmte Funktionen primitiv-rekursiv sind
- Definition der
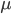 -rekursiven Funktionen
-rekursiven Funktionen - Erläuterung der Churchschen These
- Beweis der Existenz von nicht-berechenbaren Funktionen durch Diagonalisierung
Kurseinheit 5
Auch wenn die Kurseinheit mit 30 Seiten doch recht dünn ist, habe ich es irgendwie geschafft daraus ebenfalls 30 Seiten zu machen. Puh!
Die doch nicht so einfach (für mich zumindest) erschließbaren Themen waren die Standardnummerierung 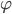 der einstelligen, evtl. partiellen, berechenbaren Funktionen
der einstelligen, evtl. partiellen, berechenbaren Funktionen 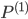 , die Standarskomplexität
, die Standarskomplexität 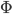 , das utm-, smn- und das
, das utm-, smn- und das 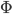 -Theorem inkl. einiger lustiger Sätze wie dem Äquivalenzsatz von Rogers oder dem Rekursionssatz inkl. Anwendungsbereichen in der Selbstreproduktion.
-Theorem inkl. einiger lustiger Sätze wie dem Äquivalenzsatz von Rogers oder dem Rekursionssatz inkl. Anwendungsbereichen in der Selbstreproduktion.
Alles in Allem eine sehr gelungene Kurseinheit, die (für mich) bis jetzt durchaus die Niveauspitze darstellt. Oder ich hatte zu wenig Kaffee.
TIA: Standardnummerierung 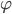 , Standardkomplexität
, Standardkomplexität 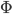 und das
und das 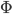 -Theorem (Lernziele KE5, 1/3)
-Theorem (Lernziele KE5, 1/3)
- Erläuterung der Definition der Standardnummerierung
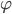 von
von 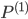
- Erläuterung des
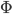 -Theorems
-Theorems - Beweis der Berechenbarkeit von
 (als Vorarbeit zum utm-Theorem)
(als Vorarbeit zum utm-Theorem)
Exkurs: utm-Theorem und Zusammenhang zu Programmiersprachen
- Zusammenhang zwischen
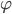 , dem utm-Theorem und Programmiersprachen
, dem utm-Theorem und Programmiersprachen
TIA: utm-Theorem (Lernziele KE5, 2/3)
- Anwendung und Erläuterung des utm-Theorems
TIA: smn-Theorem, Äquivalenzsatz von Rogers und Rekursionssatz (Lernziele KE5, 3/3)
- Erklärung und Anwendung des smn-Theorems
- Erläuterung des Äquivalenzsatzes für Nummerierungen/Programmiersprachen (Rogers)
- Formulieren des Rekursionssatzes
Kurseinheit 6
Und als ich dachte, dass mehr als drei Beiträge zu einer Kurseinheit nicht gehen, kam Kurseinheit 6. Mit insg. 26 Seiten ist das wahrscheinlich der längste Beitrag zu einer Kurseinheit.
Die Themenvielfalt ist hier aber auch so groß, dass jedes Thema einen eigenen Kurs wert wäre: Rekursive und rekursiv aufzählbare Mengen und ihre Eigenschaften, Nachweis dieser Eigenschaften und Zusammenhang zwischen diesen, Bild- und Projektionssatz, Halte- und Selbstanwendbarkeitsproblem, erste Übungen der Reduktion, der wichtige Satz von Rice, das Äquivalenz- und Korrektheitsproblem und der Gödel'sche Unvollständigkeitssatz.
Nach dieser KE bin ich wirklich überzeugt, dass beide Teile des Kurses eig. mindestens eigene 10 ECTS verdient hätten.
TIA: Rekursive und rekursiv-aufzählbare Mengen (Lernziele KE6, 1/4)
- Definition rekursiver und rekursiv aufzählbarer Mengen von Zahlen und Wörtern
- Abschlusseigenschaften rekursiver und rekursiv aufzählbarer Mengen
- Nachweis der Rekursivität/Entscheidbarkeit von Mengen
- Nachweis der rekursiven Aufzählbarkeit/Semi-entscheidbarkeit von Mengen
- Erläuterung des Zusammenhangs zwischen rekursiven und rekursiv-aufzählbaren Mengen
TIA: Bild- und Projektionssatz (Lernziele KE6 2/4)
- Charakterisierung der r.a. Mengen durch Bild- und Projektionssatz
TIA: Halte- Äquivalenz- und Korrektheitsproblem, Reduzierbarkeit, Satz von Rice (Lernziele KE6, 3/4)
- Halte- und Selbstanwendbarkeitsproblem
- Erklärung der Reduzierbarkeit und Methode der Reduktion
- Satz von Rice
- Äquivalenz- und Korrektheitsproblem
- Gödel'scher Unvollständigkeitssatz
TIA: Gödel'scher Unvollständigkeitssatz (Lernziele KE6, 4/4)
- Detailbetrachtung: Gödel'scher Unvollständigkeitssatz, Peano und Beweissysteme
Kurseinheit 7
Das ist nun die letzte Kurseinheit des ersten teils der theoretischen Informatik.
Alle Berechenbarkeitskonzepte, die wir vorher hatten, haben wir nur auf den natürlichen Zahlen (Registermaschinen) und Worten über einem Alphabet (durch Turingmaschinen) definiert. Was wir vergessen haben, waren die reellen Zahlen. Auf diese lassen sich die behandelten Konzepte nicht einfach so übertragen. Da bedarf es schon etwas mehr Anstrengung.
TIA: Berechenbarkeit auf anderen Mengen (Lernziele KE7, 1/2)
- Definition der Berechenbarkeitskonzepte, welche durch eien Nummerierung auf einer Menge
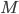 induziert werden:
induziert werden: 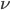 -rekursiv,
-rekursiv, 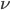 -r.a,
-r.a, 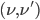 -berechenbar
-berechenbar - Nachweis der
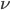 -Rekursivität und
-Rekursivität und 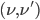 -Berechenbarkeit
-Berechenbarkeit
TIA: Berechenbarkeit auf anderen Mengen (Lernziele KE7, 2/2)
- Erklärung der Reduzierbarkeit und Äquivalenz von Nummerierungen
- Konstruktion einer reellen Zahl
 einer Funktion
einer Funktion  , die nicht im Bild von
, die nicht im Bild von 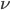 liegt
liegt - Definition berechenbarer Funktionen
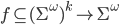
- Definition der Cauchy-Darstellung der reellen Zahlen
- Zeigen, dass z.B.
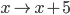
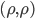 -berechenbar ist
-berechenbar ist
Zusammenfassungen theoretische Informatik B (01658)
Kurseinheit 1
Die erste Kurseinheit der theoretischen Informatik B startet direkt mit der Frage nach den Komplexitätsmaßen in Bezug auf Turingmaschinen: die wichtigsten Ressourcen sind Band und Zeit. Diese werden in dieser Kurseinheit erstmals definiert und anschließend weiter ausgebaut, Zusammenhänge hergestellt und die Bandreduktionssätze angesprochen.
Maschinenmodelle und Komplexitätsklassen (Lernziele KE1)
- Definition der Komplexitätsmaße Zeit und Band für Turing-Maschinen
- Definition der Komplxitätsklassen
- Zusammenhang zwischen Band- und Zeitkomplexität
- Darstellung der Aussage der Bandreduktionssätze und Beweisidee
Kurseinheit 2
Bei dieser Kurseinheit kümmern wir uns um die Separation von Komplexitätsklassen bei Zeit und Band und wenden diese an um zu zeigen, dass Funktionen in unterschiedlichen Komplexitätsklassen sind. Mittels Hierarchiesätzen können wir auch eine Hierarchie auf diesen Komplexitätsklassen bilden.
Separations- und Hierarchiesätze (Lernziele KE2)
- Verstehen des Verfahrens von Separations- und Hierarchiesätzen
- Voraussetzung für Separations- und Hierarchiesätze benennen und begründen
- Anwendung der Sätze zum Beweis von Separationen und echten Inklusionen
- Definition von band- und zeitkonstruierbaren Funktionen
- Beschreibung des Beweises von
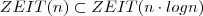 (fehlt leider)
(fehlt leider) - Beweis der Beziehungen zwischen den Klassen P, LOGSPACE, PSPACE
Exkurs/Vorschau: P-NP-Problem und das Problem des Handlungsreisenden
- Kleine Vorschau auf die kommenden Kurseinheiten und detaillierte Besprechung des TSP sowie des P-NP-Problems
Kurseinheit 3
In KE3 geht es um die nichtdeterministische Komplexität, Kontrollturingmaschinen und nichtdeterministische Turingmaschinen, die Überführung der beiden Modelle ineinander innerhalb der gleichen Band- und Zeitschranken, erste Erläuterung der polynomiellen Reduktion und der NP-Vollständigkeit von Mengen.
Alles in allem eine gelungene und wichtige Kurseinheit.
TIB: Nichtdeterministische Komplexität (Lernziele KE3)
- Erklärung der Modelle der KTM und der NTM
- Äquivalenz der Modelle begründen
- Definition nichtdeterministischer Komplixitätsmaße und -klassen
- Zusammenhang zwischen deterministischen und nichtdeterministischen Komplexitätsklassen
- Definition von
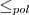
- Erklärung der Vollständigkeit
Kurseinheit 4
Nachdem wir in der letzten Kurseinheit die 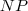 -Komplexität hatte, kommen wir hier zu
-Komplexität hatte, kommen wir hier zu 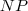 -vollständigen Problemen:
-vollständigen Problemen:  -Domino (Kachelproblem) und
-Domino (Kachelproblem) und  bilden die Grundpfeiler. Wir zeigen die Vollständigkeitsbeweise und polynomielle Reduktionen dieser Probleme, geben ein paar weitere
bilden die Grundpfeiler. Wir zeigen die Vollständigkeitsbeweise und polynomielle Reduktionen dieser Probleme, geben ein paar weitere 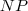 -vollständige Probleme an (
-vollständige Probleme an ( wird detailliert besprochen) und zeigen, warum
wird detailliert besprochen) und zeigen, warum  vollständig für
vollständig für 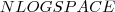 ist.
ist.
TIB: Nichtdeterministische Probleme (Lernziele KE4 1/2)
- Wie ist die Idee des Vollständigkeitsbeweises zu
 -Domino?
-Domino? - Wie beweist man die Vollständigkeit einer Menge?
TIB: Nichtdeterministische Probleme (Lernziele KE4 2/2)
- Wie ist der Vollständigkeitsbeweis zu
 ?
? - Wie führt man eine einfache, polynomielle Reduktion
 aus?
aus? - Angabe einiger NP-vollständigen Probleme, Details zu

- Warum ist
 vollständig für
vollständig für 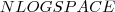 ?
?
Kurseinheit 5
Mit dieser Kurseinheit beginnt das große Thema Grammatiken/Sprache, welches uns bis KE7 begleiten wird.
Überabzählbarkeit, Noam Chomsky, Regeln der Typ-0/Typ-1/Typ-2/Typ-3-Grammatiken, die Beziehung zwischen semi-entscheidbaren/rekursiv-aufzählbaren Wortmengen, Beziehungen zwischen Grammatik und Turingmaschine, die Inklusionsbeziehung zwischen den Sprachklassen, die Beziehung zwischen regulären Mengen und rechtslinearen Grammatiken, reguläre Ausdrücke, die Transformation von Grammatiken in die rechtslineare Normalform (inkl. Beispiel) sind die Stichworte in dieser Kurseinheit.
TIB: Grammatiken und reguläre Sprachen (Lernziele KE5 1/1)
- Was ist eine Grammatik
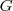 , wie definiert man die Sprache
, wie definiert man die Sprache  ?
? - Welche Sprachklasse wird durch Grammatiken definiert?
- Was sind Typ-1-, Typ-2-, Typ-3-Grammatiken?
- Wie definiert man regulären Mengen?
- Welche Sprache wird durch einen regulären Ausdruck definiert?
- Was ist eine rechtslineare Grammatik?
- Wie zeigt man, dass die reguläre Sprache von rechtslinearen Grammatiken erzeugt wird?
- Wie transformiert man eine rechtslineare Grammatik in eine rechtslineare Normalform?
Kurseinheit 6
Mittels endlichen Automaten werden hier die regulären Sprachen erkannt. Ebenfalls definieren wir hier nichtdeterministische Automaten, Vollständigkeit, Überführungsfunktionen, transitive Hüllen usw. und zeigen diese Definitionen auch an einem Beispiel und stellen mit diesem Automaten fest ob ein Wort in einer Sprache ist oder nicht. Auch konstruieren wir zu einem nichtdeterminierten Automaten einen determinierten, der die selbe Sprache erkennt (was bei Kellerautomaten nicht funktioniert, aber dazu in KE7 mehr).
Wir setzen im nächsten Beitrag reguläre Ausdrücke in Beziehung mit endlichen Automaten anhand eines Beispiels. Auch betrachten wir die Abgeschlossenheit der regulären Sprachen mit bestimmten Operationen und die Beweisidee anhand konkreter Beispiele um dann mit dem Pumping Lemma für reguläre Sprachen und den Entscheidungsproblemen den Beitrag abzuschließen.
Der letzte Punkt führt uns zu Ableitungsbäumen kontextfreier Grammatiken mit einem grafischen Beispiel, der Eindeutigkeit von Grammatiken (wichtig!) und als kleinen Exkrus: zu Syntaxbäumen.
TIB: Endliche Automaten und kontextfreie Grammatiken (Lernziele KE6 1/3)
- Wie definiert man die von einem endlichen Automaten erkannte Sprache?
- Wie kann man zu einem nichtdeterminierten endlichen Automaten einen determinierten konstruieren, der dieselbe Sprache erkennt?
TIB: Endliche Automaten und kontextfreie Grammatiken (Lernziele KE6 2/3)
- Wie konstruiert man zu einem endlichen Automaten
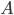 einen regulären Ausdruck
einen regulären Ausdruck 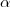 mit
mit  ?
? - Wie zeigt man, dass die regulären Sprache unter den in Satz 8.4.1 genannten Operationen abgeschlossen sind (Beweisidee)?
- Welche "Probleme" sind für reguläre Sprachen entscheidbar?
- Wie lautet das Pumping-Lemma für reguläre Sprachen? Wie kann man es verwenden um nachzuweisen, dass eine Sprache nicht regulär ist?
TIB: Endliche Automaten und kontextfreie Grammatiken (Lernziele KE6 3/3)
- Was sind Ableitungsbäume kontextfreier Grammatiken?
- Wann ist eine kontextfreie Grammatik bzw. Sprache eindeutig?
Kurseinheit 7
In dieser Kurseinheit dreht sich alles um Kellerautomaten. Zunächst kümmern wir uns um die Chomsky-Normalform und wie man sie erzeugt. Anschließend wird das Pumping-Lemma für kontextfreie Sprachen erklärt und an zwei detaillierten Beispielen (positiv und negativ) angewandt.
Im letzten Beitrag widmen wir uns dann um determinierte Kellerautomaten und die (Unter-)Sprachklasse, die von ihnen erkannt wird. Anhand eines Beispiels wird gezeigt, dass die Klasse der deterministisch kontextfreien Sprachen nicht abgeschlossen ist gegen Vereinigung und die Vereinigung zweier deterministisch kontextfreier Sprachen nur eine kontextfreie Sprache erzeugt. Diese Sprache wird dann in eine Grammatik und dann in einen nichtdeterministischen Kellerautomaten übersetzt. Zuletzt geht es dann um die Abschlusseigenschaften dieser Sprachklasse und die Entscheidungsprobleme in diesen.
TIB: Kontextfreie Sprachen und Kellerautomaten (Lernziele KE7 1/3)
- Wann ist eine Grammatik in Chomsky-Normalform und wie konstruiert man eine solche aus einer beliebigen kontextfreien Grammatik?
- Was besagt das Pumping-Lemma für kontextfreie Sprachen und wie wendet man es an?
TIB: Kontextfreie Sprachen und Kellerautomaten (Lernziele KE7 2/3)
- Wie sind Kellerautomaten und die von ihnen akzeptierte Sprache definiert?
- Wie zeigt man, dass Kellerautomaten genau die kontextfreien Sprachen erkennen?
TIB: Kontextfreie Sprachen und Kellerautomaten (Lernziele KE7 3/3)
- Was sind determinierte Kellerautomaten?
- Ist jede kontextfreie Sprache deterministisch? Mit Begründung!
- Sind die kontextfreien bzw. deterministisch kontextfreien Sprachen abgeschlossen unter Vereinigung, Durchschnitt, Komplement und Schnitt mit regulären Mengen?
- Welche der folgenden Probleme sind für kontextfreie Grammatiken entscheidbar/unentscheidbar?
